6.5: Distribución de Muestreo y Teorema del Límite Central

Última actualización
Guardar como PDF

Page ID: 149820

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ahora tienes la mayoría de las habilidades para iniciar la inferencia estadística, pero necesitas un concepto más.

En primer lugar, sería útil exponer qué es la inferencia estadística en términos más precisos.

Definición$\PageIndex{1}$:Statistical Inference

Inferencia estadística: para tomar decisiones precisas sobre los parámetros a partir de la estadística.

Cuando dice “decisión precisa”, quieres poder medir qué tan precisa. Se mide la precisión con la probabilidad. Tanto en distribuciones binomiales como normales, necesitabas saber que la variable aleatoria seguía cualquiera de las dos distribuciones. Necesitas saber cómo se distribuye la estadística y luego puedes encontrar probabilidades. En otras palabras, necesitas conocer la forma de la media de la muestra o cualquier estadística sobre la que quieras tomar una decisión.

¿Cómo se distribuye la estadística? Esto se responde con una distribución de muestreo.

Definición$\PageIndex{2}$: Sampling Distribution

Distribución de Muestreo: cómo se distribuye un estadístico muestral cuando se toman ensayos repetidos de tamaño n.

Ejemplo$\PageIndex{1}$ sampling distribution

Supongamos que lanzas un centavo y cuentas la frecuencia con la que sale una cabeza. La variable aleatoria es x = número de cabezas. La distribución de probabilidad (pdf) de esta variable aleatoria se presenta en la Figura$\PageIndex{1}$.

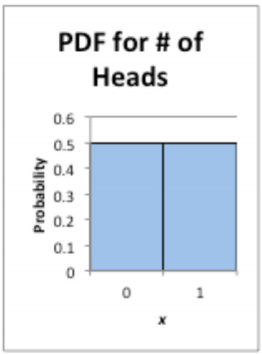Captura de pantalla (114) .png — Figura$\PageIndex{1}$: Distribución de Variable Aleatoria

Solución

Repita este experimento 10 veces, lo que significa n = 10. Aquí está el conjunto de datos:

{1, 1, 1, 1, 0, 0, 0, 0, 0, 0}. La media de esta muestra es 0.4. Ahora toma otra muestra. Aquí está ese conjunto de datos:

{1, 1, 1, 0, 1, 0, 1, 1, 0, 0}. La media de esta muestra es 0.6. Otra muestra se ve así:

{0, 1, 0, 1, 1, 1, 1, 1, 0, 1}. La media de esta muestra es 0.7. Repite esto 40 veces. Podrías obtener estos medios:

Tabla$\PageIndex{1}$: Medias de la muestra cuando n=10
0.4	0.6	0.7	0.3	0.3	0.2	0.5	0.5	0.5	0.5
0.4	0.4	0.5	0.7	0.7	0.6	0.4	0.4	0.4	0.6
0.7	0.7	0.3	0.5	0.6	0.3	0.3	0.8	0.3	0.6
0.4	0.3	0.5	0.6	0.5	0.6	0.3	0.5	0.6	0.2

Ejemplo$\PageIndex{2}$ contiene la distribución de estas medias de muestra (solo cuente cuántas de cada número hay y luego dividirlas por 40 para obtener la frecuencia relativa).

Tabla$\PageIndex{2}$: Distribución de las medias de la muestra cuando n=10
Media de la Muestra	Probabilidad
0.1	0
0.2	0.05
0.3	0.2
0.4	0.175
0.5	0.225
0.6	0.2
0.7	0.125
0.8	0.025
0.9	0

La figura$\PageIndex{2}$ contiene el histograma de estas medias de muestra.

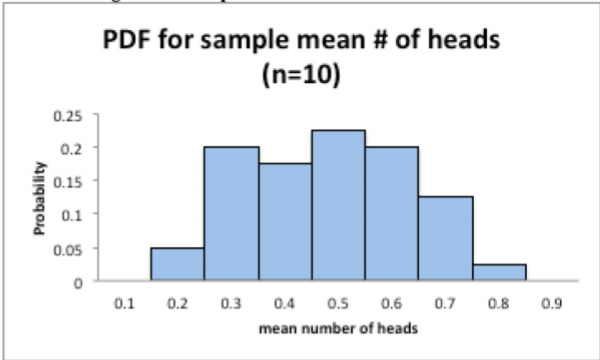Captura de pantalla (115) .png — Figura$\PageIndex{2}$: Histograma de medias de la muestra cuando n=10

Esta distribución (representada gráficamente por el histograma) es una distribución de muestreo. Eso es todo lo que es una distribución de muestreo. Se trata de una distribución creada a partir de estadísticas.

Observe que el histograma no se parece en nada al histograma de la variable aleatoria original. Tampoco se parece en nada a una distribución normal, que es la única que realmente sabes encontrar probabilidades. Concedido tienes el binomio, pero lo normal es mejor.

¿Cómo se ve esta distribución si en lugar de repetir el experimento 10 veces lo repites 20 veces en su lugar?

$\PageIndex{3}$El ejemplo contiene 40 medias cuando el experimento de voltear la moneda se repite 20 veces.

Tabla$\PageIndex{3}$: Medias de la muestra cuando n=20
0.5	0.45	0.7	0.55	0.65	0.6	0.4	0.35	0.45	0.6
0.5	0.5	0.65	0.5	0.5	0.35	0.55	0.4	0.65	0.3
0.4	0.5	0.45	0.45	0.65	0.7	0.6	0.5	0.7	0.7
0.7	0.45	0.35	0.6	0.65	0.55	0.35	0.4	0.55	0.6

Ejemplo$\PageIndex{3}$ contiene la distribución muestral de las medias muestrales.

Tabla$\PageIndex{3}$: Distribución de las medias de la muestra cuando n=20
Media	Probabilidad
0.1	0
0.2	0
0.3	0.125
0.4	0.2
0.5	0.3
0.6	0.25
0.7	0.125
0.8	0
0.9	0

Este histograma de la distribución de muestreo se muestra en la Figura$\PageIndex{3}$.

Captura de pantalla (116) .png — Figura$\PageIndex{3}$: Histograma de Medias Muestras Cuando n=20

Observe que este histograma de la media de la muestra se ve aproximadamente simétrico y casi podría llamarse normal. ¿Y si sigues aumentando n? ¿Cómo será la distribución muestral de la muestra media? En otras palabras, ¿cómo se ve la distribución de muestreo de$\overline{x}$ a medida que n se hace aún más grande?

Esto depende de cómo se distribuya la distribución original. En Ejemplo$\PageIndex{1}$, la variable aleatoria fue de aspecto uniforme. Pero a medida que n aumentaba a 20, la distribución de la media se veía aproximadamente normal. ¿Y si la distribución original era normal? ¿Qué tan grande tendría que ser n? Antes de que se responda a esa pregunta, se necesita otro concepto.

Nota

Supongamos que tiene una variable aleatoria que tiene una media poblacional,$\mu$, y una desviación estándar poblacional,$\sigma$. Si se toma una muestra de tamaño n, entonces la media muestral,$\overline{x}$ tiene una media$\mu_{\overline{x}}=\mu$ y desviación estándar de$\sigma_{\overline{x}}=\dfrac{\sigma}{\sqrt{n}}$. La desviación estándar de$\overline{x}$ es menor porque al tomar la media estás promediando los valores extremos, lo que hace que la distribución de la variable aleatoria original se extienda.

Ya conoces el centro y la variabilidad de$\overline{x}$. También quieres conocer la forma de la distribución de$\overline{x}$. Esperas que sea normal, ya que sabes encontrar probabilidades usando la curva normal. El siguiente teorema te dice el requisito de haber distribuido$\overline{x}$ normalmente.

Teorema$\PageIndex{1}$ central limit theorem

Supongamos que una variable aleatoria es de cualquier distribución. Si se toma una muestra de tamaño n, entonces la media de la muestra,$\overline{x}$, se distribuye normalmente a medida que n aumenta.

Lo que esto dice es que no importa cómo se vea x, se$\overline{x}$ vería normal si n es lo suficientemente grande. Ahora bien, ¿qué tamaño de n es lo suficientemente grande? Eso depende de cómo se distribuya x en primer lugar. Si la variable aleatoria original se distribuye normalmente, entonces n solo necesita ser 2 o más puntos de datos. Si la variable aleatoria original es algo en forma de montículo y simétrica, entonces n necesita ser mayor o igual a 30. A veces el tamaño de la muestra puede ser menor, pero esta es una buena regla general. El tamaño de la muestra puede tener que ser mucho mayor si la variable aleatoria original está realmente sesgada de una manera u otra.

Ahora que ya sabes cuándo la media muestral se verá como una distribución normal, entonces puedes encontrar la probabilidad relacionada con la media muestral. Recuerde que la media de la media de la muestra es solo la media de los datos originales ($\mu_{\overline{x}}=\mu$), pero la desviación estándar de la media de la muestra$\sigma_{\overline{x}}$, también conocida como el error estándar de la media, es en realidad$\sigma_{\overline{x}}=\dfrac{\sigma}{\sqrt{n}}$. Asegúrate de usar esto en todos los cálculos. Si está utilizando la puntuación z, la fórmula cuando se trabaja con$\overline{x}$ es$z=\dfrac{\overline{x}-\mu_{\overline{x}}}{\sigma_{\overline{x}}}=\dfrac{\overline{x}-\mu}{\sigma / \sqrt{n}}$. Si está utilizando la calculadora TI-83/84, entonces la entrada sería normalcdf (límite inferior, límite superior,$\mu$,$\sigma / \sqrt{n}$). Si estás usando R, entonces la entrada sería pnorm ($\overline{x}, \mu, \sigma / \operatorname{sqrt}(n) $) para encontrar el área a la izquierda de$\overline{x}$. Recuerda restar pnorm ($\overline{x}, \mu, \sigma / \operatorname{sqrt}(n))$) de 1 si quieres el área a la derecha de$\overline{x}$.

Ejemplo$\PageIndex{2}$ Finding probabilities for sample means

El peso al nacer de los bebés varones de ascendencia europea que dieron a luz a las 40 semanas normalmente se distribuye con una media de 3687.6 g con una desviación estándar de 410.5 g (Janssen, Thiessen, Klein, Whitfield, MacNab & Cullis-Kuhl, 2007). Supongamos que hubo nueve niños de ascendencia europea nacidos en un día determinado y se calcula el peso medio al nacer.

Anote la variable aleatoria.
¿Cuál es la media de la muestra?
¿Cuál es la desviación estándar de la muestra media?
¿En qué distribución se distribuye la media de la muestra?
Encuentra la probabilidad de que el peso medio de los nueve niños nacidos sea menor a 3500.4 g.
Encuentra la probabilidad de que el peso medio de los nueve bebés nacidos sea inferior a 3452.5 g.

Solución

a. x = peso al nacer de los bebés varones (Nota: la variable aleatoria es algo que se mide, y no es el peso medio al nacer. Se calcula el peso medio al nacer.)

b.$\mu_{\overline{x}}=\mu=3687.6 \mathrm{g}$

c.$\sigma_{\overline{x}}=\dfrac{\sigma}{\sqrt{n}}=\dfrac{410.5}{\sqrt{9}}=\dfrac{410.5}{3} \approx 136.8 \mathrm{g}$

d. Dado que la variable aleatoria original se distribuye normalmente, entonces la media de la muestra se distribuye normalmente.

e. Usted está buscando el$P(\overline{x}<3500.4)$. Utiliza el comando normalcdf en la calculadora. Recuerde usar la desviación estándar que encontró en la parte c. Sin embargo, para reducir el error de redondeo, escriba la división en el comando. En el TI-83/84 tendrías

$P(\overline{x}<3500.4)=\text { normalcdf }(-1 E 99,3500.4,3687.6,410.5 \div \sqrt{9}) \approx 0.086$

En R tendrías

$P(\overline{x}<3500.4)=\text { pnorm }(3500.4,3687.6,410.5 / s q r(9)) \approx 0.086$

Existe un 8.6% de probabilidad de que el peso medio al nacer de los nueve niños nacidos sea inferior a 3500.4 g. Dado que esto es más del 5%, esto no es inusual.

f. usted está buscando el$P(\overline{x}<3452.5)$.

En TI-83/84:

$P(\overline{x}<3452.5)=\text { normalcdf }(-1 E 99,3452.5,3687.6,410.5 \div \sqrt{9}) \approx 0.043$

En R:

$P(\overline{x}<3452.5)=\text { pnorm }(3452.5,3687.6,410.5 \div \sqrt{9}) \approx 0.043$

Existe una probabilidad de 4.3% de que el peso medio al nacer de los nueve niños nacidos sea inferior a 3452.5 g, ya que esto es menor al 5%, esto sería un evento inusual. Si realmente sucedió, entonces puedes pensar que hay algo inusual en esta muestra. Tal vez algunos de los nueve bebés nacieron como múltiplos, lo que reduce el peso medio, o algunos o todos los bebés no eran de ascendencia europea (de hecho el peso medio de los bebés varones del sur de Asia es 3452.5 g), o algunos nacieron antes de las 40 semanas, o los bebés nacieron a grandes altitudes.

Ejemplo$\PageIndex{3}$ finding probabilities for sample means

La edad en la que las mujeres estadounidenses tienen relaciones sexuales por primera vez es en promedio de 17.4 años, con una desviación estándar de aproximadamente 2 años (“The Kinsey institute”, 2013). Esta variable aleatoria no se distribuye normalmente, aunque tiene una forma algo de montículo.

Anote la variable aleatoria.
Supongamos que se toma una muestra de 35 hembras americanas. Encuentra la probabilidad de que la edad media que estas 35 hembras tuvieron por primera vez relaciones sexuales sea mayor a 21 años.

Solución

a. x = edad en la que las hembras americanas primero tienen relaciones sexuales.

b. Aunque la variable aleatoria original no se distribuye normalmente, el tamaño de la muestra es superior a 30, por el teorema del límite central la media de la muestra se distribuirá normalmente. La media de la muestra es$\mu_{\mathrm{\overline{x}}}=\mu=17.4$ años. La desviación estándar de la media muestral es$\sigma_{\overline{x}}=\dfrac{\sigma}{\sqrt{n}}=\dfrac{2}{\sqrt{35}} \approx 0.33806$. Tienes toda la información que necesitas para usar el comando normal en tu tecnología. Sin el teorema del límite central, no podrías usar el comando normal, y no podrías responder a esta pregunta.

En el TI-83/84:

$P(\overline{x}>21)=\text { normalcdf }(21,1 E 99,17.4,2 \div \sqrt{35}) \approx 9.0 \times 10^{-27}$

En R:

$P(\overline{x}>21)=1-\text { pnorm }(21,17.4,2 / \operatorname{sqrt} (35)) \approx 9.0 \times 10^{-27}$

La probabilidad de que una media muestral de 35 mujeres sea mayor de 21 años cuando tuvieron su primera relación sexual es muy pequeña. Esto es extremadamente improbable que suceda. Si lo hace, puede hacer que te preguntes sobre la muestra. ¿Podría haber aumentado la población a partir de los 17.4 años que se afirmaba en el artículo? ¿La muestra no pudo haber sido aleatoria, y en su lugar haber sido un grupo de mujeres que tenían creencias similares sobre las relaciones sexuales? Estas preguntas, y más, son las que te gustaría hacer como investigador.

Testo

Ejercicio$\PageIndex{1}$

Una variable aleatoria no se distribuye normalmente, sino que tiene forma de montículo. Tiene una media de 14 y una desviación estándar de 3.
1. Si toma una muestra de tamaño 10, ¿puede decir cuál es la forma de la distribución muestral para la media de la muestra? ¿Por qué?
2. Para una muestra de tamaño 10, indique la media de la media de la muestra y la desviación estándar de la media de la muestra.
3. Si tomas una muestra de talla 35, ¿puedes decir cuál es la forma de la distribución de la muestra media? ¿Por qué?
4. Para una muestra de tamaño 35, indique la media de la media de la muestra y la desviación estándar de la media de la muestra.
Normalmente se distribuye una variable aleatoria. Tiene una media de 245 y una desviación estándar de 21.
1. Si tomas una muestra de tamaño 10, ¿puedes decir cuál es la forma de la distribución para la muestra media? ¿Por qué?
2. Para una muestra de tamaño 10, indique la media de la media de la muestra y la desviación estándar de la media de la muestra.
3. Para una muestra de tamaño 10, encuentre la probabilidad de que la media muestral sea superior a 241.
4. Si tomas una muestra de talla 35, ¿puedes decir cuál es la forma de la distribución de la muestra media? ¿Por qué?
5. Para una muestra de tamaño 35, indique la media de la media de la muestra y la desviación estándar de la media de la muestra.
6. Para una muestra de tamaño 35, encuentra la probabilidad de que la media muestral sea mayor a 241.
7. Compara tus respuestas en las partes d y f. ¿Por qué una es más pequeña que la otra?
El salario inicial medio para las enfermeras es de $67,694 a nivel nacional (“Staff nurse -”, 2013). La desviación estándar es de aproximadamente $10,333. El salario inicial normalmente no se distribuye sino que tiene forma de montículo. Se toma una muestra de 42 salarios iniciales para enfermeras.
1. Anote la variable aleatoria.
2. ¿Cuál es la media de la muestra?
3. ¿Cuál es la desviación estándar de la muestra media?
4. ¿Cuál es la forma de la distribución muestral de la media de la muestra? ¿Por qué?
5. Encuentra la probabilidad de que la media de la muestra sea superior a $75,000.
6. Encuentra la probabilidad de que la media de la muestra sea menor a $60,000.
7. Si encontraras una media muestral de más de 75,000 dólares ¿te parece inusual? ¿Qué podrías concluir?
Según el Proyecto MONICA de la OMS la presión arterial media para las personas en China es de 128 mmHg con una desviación estándar de 23 mmHg (Kuulasmaa, Hense & Tolonen, 1998). La presión arterial normalmente se distribuye.
1. Anote la variable aleatoria.
2. Supongamos que se toma una muestra de tamaño 15. Indicar la forma de la distribución de la media muestral.
3. Supongamos que se toma una muestra de tamaño 15. Indicar la media de la media muestral.
4. Supongamos que se toma una muestra de tamaño 15. Indicar la desviación estándar de la media de la muestra.
5. Supongamos que se toma una muestra de tamaño 15. Encuentra la probabilidad de que la presión arterial media de la muestra sea superior a 135 mmHg.
6. ¿Sería inusual encontrar una muestra media de 15 personas en China de más de 135 mmHg? ¿Por qué o por qué no?
7. Si encontraste que una muestra media para 15 personas en China sea más de 135 mmHg, ¿qué podrías concluir?
El tamaño de los peces es muy importante para la pesca comercial. Un estudio realizado en 2012 encontró que la longitud del bacalao atlántico capturado en redes en Karlskrona tenía una media de 49.9 cm y una desviación estándar de 3.74 cm (Ovejgard, Berndt & Lunneryd, 2012). La longitud de los peces se distribuye normalmente. Se toma una muestra de 15 peces.
1. Anote la variable aleatoria.
2. Encuentra la media de la media de la muestra.
3. Encontrar la desviación estándar de la media de la muestra
4. ¿Cuál es la forma de la distribución de la muestra media? ¿Por qué?
5. Encuentra la probabilidad de que la longitud media muestral del bacalao del Atlántico sea menor a 52 cm.
6. Encuentra la probabilidad de que la longitud media muestral del bacalao del Atlántico sea superior a 74 cm.
7. Si encontraste que la longitud media de la muestra para el bacalao del Atlántico es superior a 74 cm, ¿qué podrías concluir?
Los niveles medios de colesterol de las mujeres de 45 a 59 años en Ghana, Nigeria y Seychelles son de 5.1 mmol/l y la desviación estándar es de 1.0 mmol/l (Lawes, Hoorn, Law & Rodgers, 2004). Supongamos que los niveles de colesterol se distribuyen normalmente.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que una mujer de 45-59 años en Ghana tenga un nivel de colesterol superior a 6.2 mmol/l (considerado un nivel alto).
3. Supongamos que los médicos deciden volver a probar el nivel de colesterol de la mujer y promediar los dos valores. Encuentra la probabilidad de que el nivel medio de colesterol de esta mujer para las dos pruebas esté por encima de 6.2 mmol/l.
4. Supongamos que los médicos que son muy conservadores deciden probar el nivel de colesterol de la mujer por tercera vez y promediar los tres valores. Encuentra la probabilidad de que el nivel medio de colesterol de esta mujer para las tres pruebas esté por encima de 6.2 mmol/l.
5. Si el nivel medio de colesterol de la muestra para esta mujer después de tres pruebas es superior a 6.2 mmol/l, ¿qué podrías concluir?
En Estados Unidos, los machos de entre 40 y 49 años comen en promedio 103.1 g de grasa todos los días con una desviación estándar de 4.32 g (“Qué comemos”, 2012). La cantidad de grasa que come una persona normalmente no se distribuye sino que es relativamente en forma de montículo.
1. Anote la variable aleatoria.
2. Encuentra la probabilidad de que una muestra de cantidad media de ingesta diaria de grasa para 35 hombres de 40 a 59 años en Estados Unidos sea superior a 100 g.
3. Encuentra la probabilidad de que una muestra de cantidad media de ingesta diaria de grasa para 35 hombres de 40 a 59 años en Estados Unidos sea menor a 93 g.
4. Si encontraras una muestra de cantidad media de ingesta diaria de grasa para 35 hombres de 40 a 59 años en Estados Unidos menor a 93 g, ¿qué concluirías?
Un lavavajillas tiene una vida media de 12 años con una desviación estándar estimada de 1.25 años (“Esperanza de vida del aparato”, 2013). La vida útil de un lavavajillas se distribuye normalmente. Supongamos que eres fabricante y tomas una muestra de 10 lavavajillas que hiciste.
1. Anote la variable aleatoria.
2. Encuentra la media de la media de la muestra.
3. Encuentra la desviación estándar de la media muestral.
4. ¿Cuál es la forma de la distribución muestral de la media de la muestra? ¿Por qué?
5. Encuentra la probabilidad de que la media muestral de los lavavajillas sea menor a 6 años.
6. Si encontraras que la vida media de la muestra de los 10 lavavajillas es menor a 6 años, ¿pensarías que tienes algún problema con el proceso de fabricación? ¿Por qué o por qué no?

Contestar

1. a. Ver soluciones, b.$\mu_{\mathrm{\overline{x}}}=14$,$\sigma_{\overline{x}}=0.9487$, c. Ver soluciones, d.$\mu_{\mathrm{\overline{x}}}=14$,$\sigma_{\overline{x}}=0.5071$

3. a. Ver soluciones, b.$\mu_{\mathrm{\overline{x}}}=\$ 67,694$, c.$\sigma_{\overline{x}}=\$ 1594.42$, d. Ver soluciones, e.$P(\overline{x}>\$ 75,000)=2.302 \times 10^{-6}$, f.$P(\overline{x}<\$ 60,000)=6.989 \times 10^{-7}$, g. Ver soluciones

5. a. Ver soluciones, b.$\mu_{\mathrm{\overline{x}}}=49.9 \mathrm{cm}$, c.$\sigma_{\overline{x}}=0.9657 \mathrm{cm}$, d. Ver soluciones, e.$P(\overline{x}<52 \mathrm{cm})=0.9852$ f.$P(\overline{x}>74 \mathrm{cm}) \approx 0$, g. Ver soluciones

7. a. Ver soluciones, b.$P(\overline{x}>100 \mathrm{g})=0.99999$, c.$P(\overline{x}<93 \mathrm{g}) \approx 0$ o$8.22 \times 10^{-44}$, d. Ver soluciones

Fuentes de datos:

Máximo anual de precipitaciones diarias en Sydney. (2013, 25 de septiembre). Recuperado a partir de http://www.statsci.org/data/oz/sydrain.html

Esperanza de vida del aparato. (2013, 8 de noviembre). Recuperado a partir de http://www.mrappliance.com/expert/life-guide/

Bhat, R., & Kushtagi, P. (2006). Una nueva mirada a la duración del embarazo humano. Singapur Med J., 47 (12), 1044-8. Recuperado a partir de http://www.ncbi.nlm.nih.gov/pubmed/17139400

Junta Universitaria, SAT. (2012). Reporte total del perfil del grupo. Recuperado del sitio web: media.collegedigita... lGroup2012.pdf

Greater Cleveland Regional Transit Authority, (2012). Informe anual 2012. Recuperado del sitio web: http://www.riderta.com/annual/2012

Janssen, P. A., Thiessen, P., Klein, M. C., Whitfield, M. F., MacNab, Y. C., & Culliskuhl, S. C. (2007). Estándares para la medición del peso al nacer, longitud y circunferencia cefálica a término en neonatos de ascendencia europea, china y del sur de Asia. Medicina Abierta, 1 (2), e74-e88. Recuperado a partir de http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2802014/

Erupciones de soplo de Kiama. (2013, 25 de septiembre). Recuperado a partir de http://www.statsci.org/data/oz/kiama.html

Kuulasmaa, K., Hense, H., & Tolonen, H. Organización Mundial de la Salud (OMS), OMS Proyecto Mónica. (1998). Evaluación de la calidad de los datos sobre la presión arterial en el proyecto who monica (ISSN 2242-1246). Recuperado del sitio web de publicaciones electrónicas del Proyecto MONICA OMS: http://www.thl.fi/publications/monica/bp/bpqa.htm

Lawes, C., Hoorn, S., Law, M., & Rodgers, A. (2004). Colesterol alto. En M. Ezzati, A. Lopez, A. Rodgers & C. Murray (Eds.), Cuantificación comparada de riesgos para la salud (1 ed., Vol. 1, pp. 391-496). Recuperado a partir de http://www.who.int/publications/cra/.../0391-0496.pdf

Ovejard, M., Berndt, K., & Lunneryd, S. (2012). Índices de condición del bacalao atlántico (gadus morhua) sesgados por el método de captura. Revista ICES de Ciencias Marinas, doi: 10.1093/icesjms/fss145

Enfermera de personal - sueldo RN. (2013, 08 de Noviembre). Recuperado a partir de http://www1.salary.com/Staff-Nurse-RN-salary.html

El instituto Kinsey - enlaces de información sobre sexualidad. (2013, 08 de noviembre). Recuperado de www.iub.edu/~Kinsey/Resources/FAQ.html

US Department of Argriculture, Servicio de Investigación Agropecuaria. (2012). Lo que comemos en América. Recuperado del sitio web: http://www.ars.usda.gov/Services/docs.htm?docid=18349

0.4	0.6	0.7	0.3	0.3	0.2	0.5	0.5	0.5	0.5
0.4	0.4	0.5	0.7	0.7	0.6	0.4	0.4	0.4	0.6
0.7	0.7	0.3	0.5	0.6	0.3	0.3	0.8	0.3	0.6
0.4	0.3	0.5	0.6	0.5	0.6	0.3	0.5	0.6	0.2

0.4	0.6	0.7	0.3	0.3	0.2	0.5	0.5	0.5	0.5
0.4	0.4	0.5	0.7	0.7	0.6	0.4	0.4	0.4	0.6
0.7	0.7	0.3	0.5	0.6	0.3	0.3	0.8	0.3	0.6
0.4	0.3	0.5	0.6	0.5	0.6	0.3	0.5	0.6	0.2

0.4	0.6	0.7	0.3	0.3	0.2	0.5	0.5	0.5	0.5
0.4	0.4	0.5	0.7	0.7	0.6	0.4	0.4	0.4	0.6
0.7	0.7	0.3	0.5	0.6	0.3	0.3	0.8	0.3	0.6
0.4	0.3	0.5	0.6	0.5	0.6	0.3	0.5	0.6	0.2