7.1: Conceptos básicos de las pruebas de hipótesis
- Page ID
- 149740
Para entender el proceso de una prueba de hipótesis, primero es necesario tener una comprensión de lo que es una hipótesis, que es una suposición educada sobre un parámetro. Una vez que tienes la hipótesis, recolectas datos y utilizas los datos para tomar una determinación para ver si hay evidencia suficiente para demostrar que la hipótesis es cierta. Sin embargo, en las pruebas de hipótesis, realmente asumes que algo más es cierto, y luego miras tus datos para ver qué tan probable es obtener un evento que tus datos demuestran con esa suposición. Si el evento es muy inusual, entonces podrías pensar que tu suposición es en realidad falsa. Si eres capaz de decir que esta suposición es falsa, entonces tu hipótesis debe ser cierta. Esto se conoce como prueba por contradicción. Asume que lo contrario de su hipótesis es cierto y demuestras que no puede ser verdad. Si esto sucede, entonces su hipótesis debe ser cierta. Todas las pruebas de hipótesis pasan por el mismo proceso. Una vez que tienes el proceso abajo, entonces el concepto es mucho más fácil. Es más fácil ver el proceso mirando un ejemplo. Los conceptos que se necesitan se detallarán en este ejemplo.
Ejemplo\(\PageIndex{1}\) basics of hypothesis testing
Supongamos que un fabricante de la batería XJ35 afirma que la vida media de la batería es de 500 días con una desviación estándar de 25 días. Usted es el comprador de esta batería y cree que esta afirmación está inflada. Te gustaría poner a prueba tu creencia porque sin una buena razón no puedes salir de tu contrato.
¿Qué haces?
Solución
Bueno primero, debes saber lo que estás tratando de medir. Define la variable aleatoria.
Let x = vida de una batería XJ35
Ahora no solo estás tratando de encontrar diferentes valores x. Estás tratando de encontrar cuál es la verdadera media. Ya que estás tratando de encontrarla, debe ser desconocida. No crees que sean 500 días. Si lo hicieras, no estarías haciendo ninguna prueba. La verdadera media,\(\mu\), es desconocida. Eso significa que deberías definir eso también.
Let\(\mu\) = vida media de una batería XJ35
¿Y ahora qué?
Es posible que desee recolectar una muestra. ¿Qué tipo de muestra?
Podrías pedirle a los fabricantes que te den baterías, pero existe la posibilidad de que haya algún sesgo en las baterías que escogen. Para reducir la probabilidad de sesgo, lo mejor es tomar una muestra aleatoria.
¿Qué tan grande debe ser la muestra?
Una muestra de tamaño 30 o más significa que se puede utilizar el teorema del límite central. Escoja una muestra de tamaño 30.
El ejemplo\(\PageIndex{1}\) contiene los datos de la muestra recopilada:
| 491 | 485 | 503 | 492 | 282 | 490 |
| 489 | 495 | 497 | 487 | 493 | 480 |
| 483 | 504 | 501 | 486 | 478 | 492 |
| 482 | 502 | 485 | 503 | 497 | 500 |
| 488 | 475 | 478 | 490 | 487 | 486 |
Ahora, ¿qué debes hacer? Al mirar el conjunto de datos, ves que algunas de las veces están por encima de 500 y algunas están por debajo. Pero mirar todos los números es demasiado difícil. Podría ser útil calcular la media de esta muestra.
La media de la muestra es\(\overline{x} = 490\) días. Al mirar la media de la muestra, uno podría pensar que tienes razón. Sin embargo, la desviación estándar y el tamaño de la muestra también juegan un papel, así que tal vez te equivocas.
Antes de ir más lejos, es momento de formalizar algunas definiciones.
Tienes una suposición de que la vida media de una batería es inferior a 500 días. Esto se opone a lo que afirma el fabricante. Realmente hay dos hipótesis, que aquí son solo conjeturas: la que afirma el fabricante y la que usted cree. Es útil tener nombres para ellos.
Definición\(\PageIndex{1}\)
Hipótesis nula: valor histórico, reclamo o especificación del producto. El símbolo utilizado es\(H_{o}\).
Definición\(\PageIndex{2}\)
Hipótesis alternativa: lo que se quiere probar. Esto es lo que quieres aceptar como cierto cuando rechazas la hipótesis nula. Hay dos símbolos que se utilizan comúnmente para la hipótesis alternativa:\(H_{A}\) o\(H_{I}\). El símbolo\(H_{A}\) será utilizado en este libro.
En general, las hipótesis se ven así:
\(H_{o} : \mu=\mu_{o}\)
\(H_{A} : \mu<\mu_{o}\)
donde\(\mu_{o}\) solo representa el valor al que el reclamo dice que la media poblacional es en realidad igual.
Además,\(H_{A}\) puede ser menor que, mayor que, o no igual a.
Para este problema:
\(H_{o} : \mu=500\)días, ya que el fabricante dice que la vida media de una batería es de 500 días.
\(H_{A} : \mu<500\)días, ya que cree que la vida media de la batería es inferior a 500 días.
Ahora volvamos a la media. Se tiene una media muestral de 490 días. ¿Es esto lo suficientemente pequeño como para creer que tienes razón y que el fabricante está equivocado? ¿Qué tan pequeño tiene que ser?
Si calculaste una media muestral de 235, definitivamente creerías que la media poblacional es menor a 500. Pero aunque tuvieras una media muestral de 435 probablemente creerías que la media verdadera era inferior a 500. ¿Qué pasa con el 475? ¿O 483? Hay algún punto en el que dejarías de estar tan seguro de que la media poblacional es menor a 500. Ese punto separa los valores de donde estás seguro o bastante seguro de que la media es menor a 500 del área donde no estás tan seguro. ¿Cómo encuentras ese punto?
Pues depende de la cantidad de error que quieras cometer. Por supuesto que no quieres cometer ningún error, pero desafortunadamente eso es inevitable en las estadísticas. Necesitas averiguar cuánto error cometiste con tu muestra. Toma la media de la muestra, y encuentra la probabilidad de obtener otra muestra media menor que ella, asumiendo por el momento que el fabricante tiene razón. La idea detrás de esto es que quieres saber cuál es la posibilidad de que hayas podido llegar a tu media de muestra aunque la media de la población realmente sea de 500 días.
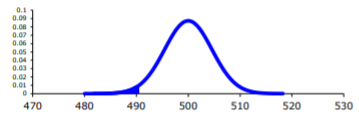
Quieres encontrar\(P\left(\overline{x}<490 | H_{o} \text { is true }\right)=P(\overline{x}<490 | \mu=500)\)
Para calcular esta probabilidad, es necesario saber cómo se distribuye la media de la muestra. Dado que el tamaño de la muestra es de al menos 30, entonces usted sabe que la media de la muestra está aproximadamente distribuida normalmente. Recuerda\(\mu_{\overline{x}}=\mu\) y\(\sigma_{\overline{x}}=\dfrac{\sigma}{\sqrt{n}}\)
Una imagen siempre es útil.
.png)
Antes de calcular la probabilidad, es útil ver cuántas desviaciones estándar alejadas de la media es la media de la muestra. Usando la fórmula para la puntuación z del capítulo 6, encontrará
\(z=\dfrac{\overline{x}-\mu_{o}}{\sigma / \sqrt{n}}=\dfrac{490-500}{25 / \sqrt{30}}=-2.19\)
Esta media de la muestra está a más de dos desviaciones estándar de la media. Eso parece bastante lejos, pero también deberías mirar la probabilidad.
En TI-83/84:
\(P(\overline{x}<490 | \mu=500)=\text { normalcdf }(-1 E 99,490,500,25 \div \sqrt{30}) \approx 0.0142\)
En R:
\(P(\overline{x}<490 \mu=500)=\text { pnorm }(490,500,25 / \operatorname{sqrt}(30)) \approx 0.0142\)
Existe una probabilidad de 1.42% de que puedas encontrar una media muestral menor de 490 cuando la media poblacional es de 500 días. Esto es realmente pequeño, por lo que lo más probable es que la suposición de que la media de la población es de 500 días sea incorrecta, y se pueda rechazar la afirmación del fabricante. Pero, ¿cómo cuantificas realmente pequeño? ¿El 5% o el 10% o el 15% es realmente pequeño? ¿Cómo decide usted?
Antes de responder a esa pregunta, se necesitan un par de definiciones más.
Definición\(\PageIndex{3}\)
Test Statistic:\(z=\dfrac{\overline{x}-\mu_{o}}{\sigma / \sqrt{n}}\) ya que se calcula como parte de la prueba de la hipótesis.
Definición\(\PageIndex{4}\)
p — valor: probabilidad de que el estadístico de prueba tome valores más extremos que el estadístico de prueba observado, dado que la hipótesis nula es verdadera. Es la probabilidad que se calculó anteriormente.
Ahora bien, ¿qué tan pequeño es lo suficientemente pequeño? Para responder a eso, realmente quieres saber los tipos de errores que puedes cometer.
En realidad sólo hay dos errores que se pueden cometer. El primer error es si dices que\(H_{o}\) es falso, cuando en realidad es cierto. Esto significa que rechazas\(H_{o}\) cuando\(H_{o}\) era verdad. El segundo error es si dices que eso\(H_{o}\) es cierto, cuando en realidad es falso. Esto significa que no rechazas\(H_{o}\) cuando\(H_{o}\) es falso. La siguiente tabla organiza esto para ti:
Tipo de errores:
| \(H_{o}\)true | \(H_{o}\)false | |
| Rechazar\(H_{o}\) | Error de tipo 1 | Sin error |
| No rechazar\(H_{o}\) | Sin error | Error de tipo II |
Así
Definición\(\PageIndex{5}\)
Tipo I Error es rechazando\(H_{o}\) cuando\(H_{o}\) es verdadero, y
Definición\(\PageIndex{6}\)
El error de tipo II no se rechaza\(H_{o}\) cuando\(H_{o}\) es falso.
Dado que estos son los errores, entonces se pueden definir las probabilidades asociadas a cada error.
Definición\(\PageIndex{7}\)
\(\alpha\)= P (error tipo I) = P (rechazar\(H_{o} / H_{o}\) es verdadero)
Definición\(\PageIndex{8}\)
\(\beta\)= P (error tipo II) = P (no rechazar\(H_{o} / H_{o}\) es falso)
\(\alpha\)también se llama el nivel de significación.
Otro concepto común que se utiliza es Poder =\(1-\beta \).
Ahora hay una relación entre\(\alpha\) y\(\beta\). No son complementos el uno del otro. ¿Cómo se relacionan?
Si\(\alpha\) aumenta eso significa que aumentarán las posibilidades de cometer un error tipo I. Es más probable que se produzca un error de tipo I. Tiene sentido que sea menos probable que cometas errores tipo II, solo porque va a estar rechazando con\(H_{o}\) más frecuencia. Estarás fallando al rechazar\(H_{o}\) menos, y por lo tanto, disminuirá la posibilidad de cometer un error tipo II. Así, a medida que\(\alpha\) aumenta,\(\beta\) disminuirá, y viceversa. Eso los hace parecer complementos, pero no son complementos. ¿Qué da? Considera un factor más: el tamaño de la muestra.
Considera si tienes una muestra más grande que sea representativa de la población, entonces tiene sentido que tengas más precisión que con una muestra más pequeña. Piénsalo de esta manera, ¿cuál confiarías más, una media muestral de 490 si tuvieras un tamaño de muestra de 35 o un tamaño de muestra de 350 (suponiendo una muestra representativa)? Por supuesto los 350 porque hay más puntos de datos y así más precisión. Si eres más preciso, entonces hay menos posibilidades de que cometas algún error. Al aumentar el tamaño de la muestra de una muestra representativa, disminuye tanto\(\alpha\) y\(\beta\).
Resumen de todo esto:
- Para cierto tamaño de muestra, n, si\(\alpha\) aumenta,\(\beta\) disminuye.
- Para cierto nivel de significancia\(\alpha\), si n aumenta,\(\beta\) disminuye.
Ahora, ¿cómo encuentras\(\alpha\) y\(\beta\)? Bueno en realidad\(\alpha\) se elige. Solo hay tres valores que generalmente se escogen para\(\alpha\): 0.01, 0.05 y 0.10. \(\beta\)es muy difícil de encontrar, por lo que generalmente no se encuentra. Si desea asegurarse de que sea pequeña, tome una muestra tan grande como pueda pagar siempre que sea una muestra representativa. Este es un uso del Poder. Quieres\(\beta\) ser pequeño y el Poder de la prueba es grande. La palabra Poder suena bien.
\(\alpha\)¿Qué selección eliges? Bueno eso depende de lo que estés trabajando. Recuerda en este ejemplo eres el comprador que está tratando de salir de un contrato para comprar estas baterías. Si creas un error tipo I, dijiste que las baterías son malas cuando no lo son, lo más probable es que el fabricante te demande. Se quiere evitar esto. Podrías elegir\(\alpha\) ser 0.01. De esta manera tienes una pequeña posibilidad de cometer un error tipo I. Por supuesto esto significa que tienes más posibilidades de cometer un error tipo II. No es gran cosa, ¿verdad? Y si las baterías se usan en marcapasos y le dices a la persona que las baterías de sus marcapasos son buenas por 500 días cuando realmente duran menos, eso podría ser malo. Si cometes un error tipo II, dices que las baterías duran 500 días cuando duran menos, entonces tienes la posibilidad de matar a alguien. Desde luego no quieres hacer esto. En este caso es posible que desee elegir\(\alpha\) como 0.10. Si ambos errores son igualmente malos, entonces elija\(\alpha\) como 0.05.
La discusión anterior es por qué la elección de\(\alpha\) depende de lo que estés investigando. Como investigador, tú eres el que necesita decidir qué\(\alpha\) nivel usar con base en tu análisis de las consecuencias de cometer cada error es.
Nota
Si un error de tipo I es realmente malo, entonces pick\(\alpha\) = 0.01.
Si un error de tipo II es realmente malo, entonces pick\(\alpha\) = 0.10
Si ninguno de los errores es malo, o ambos son igualmente malos, entonces pick\(\alpha\) = 0.05
Lo principal es escoger siempre el\(\alpha\) antes de recoger los datos e iniciar la prueba.
La discusión anterior fue larga, pero es información realmente importante. Si no sabes de qué se tratan los errores de la prueba, entonces realmente no tiene sentido sacar conclusiones con las pruebas. Asegúrate de entender cuáles son los dos errores y cuáles son las probabilidades para ellos.
Ahora es el momento de volver al ejemplo y armar todo esto. Esta es la estructura básica para probar una hipótesis, generalmente llamada prueba de hipótesis. Dado que este tiene un estadístico de prueba que involucra z, también se le llama prueba z. Y como solo hay una muestra, generalmente se le llama prueba z de una muestra.
Ejemplo\(\PageIndex{2}\) battery example revisited
- Anote la variable aleatoria y el parámetro en palabras.
- Indicar la hipótesis nula y alternativa y el nivel de significación.
- Declarar y verificar los supuestos para una prueba de hipótesis.
- Se toma una muestra aleatoria de tamaño n.
- Se conoce la derivación estándar poblacional.
- El tamaño de la muestra es de al menos 30 o la población de la variable aleatoria se distribuye normalmente.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
- Conclusión
- Interpretación
Solución
1. x = duración de la batería
\(\mu\)= vida media de una batería XJ35
2. \(H_{o} : \mu=500\)días
\(H_{A} : \mu<500\)días
\(\alpha = 0.10\)(de arriba discusión sobre las consecuencias)
3. Toda hipótesis tiene algunas suposiciones que se cumplen para asegurarse de que los resultados de la hipótesis son válidos. Los supuestos son diferentes para cada prueba. Esta prueba tiene los siguientes supuestos.
- Esto ocurrió en este ejemplo, ya que se afirmó que se tomó una muestra aleatoria de 30 vidas de batería.
- Esto es cierto, ya que se dio en el problema.
- El tamaño de la muestra fue de 30, por lo que se cumple esta condición.
4. El estadístico de prueba depende de cuántas muestras hay, qué parámetro está probando y suposiciones que deben verificarse. En este caso, hay una muestra y estás probando la media. Los supuestos fueron comprobados anteriormente.
Estadística de muestra:
\(\overline{x} = 490\)
Estadística de prueba:
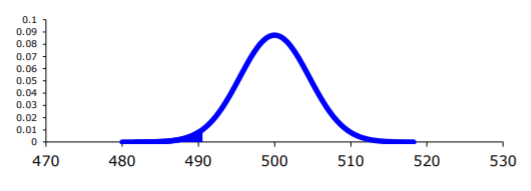
\(z=\dfrac{\overline{x}-\mu_{o}}{\sigma / \sqrt{n}}=\dfrac{490-500}{25 / \sqrt{30}}=-2.19\)
valor p:
.png)
Usando TI-83/84:
\(P(\overline{x}<490 | \mu=500)=\text { normalcdf }(-1 \mathrm{E} 99,490,500,25 / \sqrt{30}) \approx 0.0142\)
Usando R:
\(P(\overline{x}<490 | \mu=500)=\operatorname{pnorm}(490,500,25 / \operatorname{sqrt}(30)) \approx 0.0142\)
5. ¿Y ahora qué? Bueno, este valor p es 0.0142. Esto es mucho menor que la cantidad de error que aceptarías en el problema -\(\alpha\) = 0.10. Eso significa que encontrar una muestra media de menos de 490 días es inusual si\(H_{o}\) es cierto. Esto debería hacerte pensar que eso no\(H_{o}\) es cierto. Deberías rechazar\(H_{o}\).
Nota
De hecho, en general:
Rechazar\(H_{o}\) si el valor p <\(\alpha\) y
No rechazar\(H_{o}\) si el valor\(\geq \alpha\) p.
6. Desde que rechazaste\(H_{o}\), ¿qué significa esto en el mundo real? Eso es lo que va en la interpretación. Dado que rechazó la afirmación del fabricante de que la vida media de las baterías es de 500 días, entonces ahora puede creer que su hipótesis era correcta. Es decir, hay pruebas suficientes para demostrar que la vida media de la batería es inferior a 500 días.
Ahora que sabes que las baterías duran menos de 500 días, ¿deberías cancelar el contrato? Estadísticamente, hay evidencia de que las baterías no duran tanto como el fabricante dice que deberían. No obstante, con base en esta muestra sólo hay diez días menos en promedio que duran las baterías. Puede que no haya significación práctica en este caso. Diez días no parecen una gran diferencia. En realidad, si las baterías se usan en marcapasos, entonces probablemente le dirías al paciente que se reemplacen las baterías todos los años. Tiene un gran búfer ya sea que las baterías duren 490 días o 500 días. Parece que tal vez no valga la pena romper el contrato a lo largo de diez días. ¿Y si los 10 días fueran prácticamente significativos? ¿Hay alguna otra cosa que debas considerar? Podrías mirar la relación comercial con el fabricante. También podrías ver cuánto costaría encontrar un nuevo fabricante. Estas son también preguntas a considerar antes de realizar cualquier cambio. Lo que esta discusión debería mostrarle es que el hecho de que una hipótesis tenga significación estadística no significa que tenga significación práctica. La prueba de hipótesis es solo una parte de un proceso de investigación. Hay otras piezas que debes considerar.
Eso es. Así es como se ve una prueba de hipótesis. Todas las pruebas de hipótesis se realizan con los mismos seis pasos. Esos seis pasos generales se detallan a continuación.
- Anote la variable aleatoria y el parámetro en palabras. Aquí es donde estás definiendo cuáles son las incógnitas en este problema.
x = variable aleatoria
\(\mu\) = media de la variable aleatoria, si el parámetro de interés es la media. Hay otros parámetros que puedes probar, y usarías el símbolo apropiado para ese parámetro. - Indique las hipótesis nulas y alternativas y el nivel de significación
\(H_{o} : \mu=\mu_{o}\), donde\(\mu_{o}\) está la media conocida
\(H_{A} : \mu<\mu_{o}\)
\(H_{A} : \mu>\mu_{o}\), use la apropiada para su problema
\(H_{A} : \mu \neq \mu_{o}\)
También, indique su \(\alpha\)nivel aquí. - Declarar y verificar los supuestos para una prueba de hipótesis.
Cada prueba de hipótesis tiene sus propios supuestos. Se expondrán cuando se discutan las diferentes pruebas de hipótesis. - Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
Esto depende del parámetro con el que esté trabajando, cuántas muestras y los supuestos de la prueba. El valor p depende de tu\(H_{A}\). Si estás haciendo el\(H_{A}\) con el menos que, entonces es una prueba de cola izquierda, y encuentras la probabilidad de estar en esa cola izquierda. Si estás haciendo el\(H_{A}\) con el mayor que, entonces es una prueba de cola derecha, y encuentras la probabilidad de estar en la cola derecha. Si estás haciendo el\(H_{A}\) con el no igual a, entonces estás haciendo una prueba de dos colas, y encuentras la probabilidad de estar en ambas colas. Debido a la simetría, podrías encontrar la probabilidad en una cola y duplicar este valor para encontrar la probabilidad en ambas colas. - Conclusión
Aquí es donde escribes rechazar\(H_{o}\) o no rechazar\(H_{o}\). La regla es: si el valor p <\(\alpha\), entonces rechazar\(H_{o}\). Si el valor p\(\geq \alpha\), entonces no puede rechazar\(H_{o}\). - Interpretación
Aquí es donde interpretas en términos del mundo real la conclusión a la prueba. La conclusión para una prueba de hipótesis es que o bien tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad, o no tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad.
Lo siento, un concepto más sobre la conclusión e interpretación. Primero, la conclusión es que rechazas\(H_{o}\) o no lo rechazas\(H_{o}\). ¿Por qué se dijo así? Es porque nunca aceptas la hipótesis nula. Si querías aceptar la hipótesis nula, entonces ¿por qué hacer la prueba en primer lugar? En la interpretación, o tienes pruebas suficientes para demostrar que\(H_{A}\) es verdad, o no tienes pruebas suficientes para demostrar que\(H_{A}\) es verdad. No querrías ir a todo este trabajo y luego enterarte que querías aceptar el reclamo. ¿Por qué pasar por el problema? Siempre se quiere demostrar que la hipótesis alternativa es cierta. A veces puedes hacer eso y otras no puedes, no significa que hayas probado la hipótesis nula; solo significa que no puedes probar la hipótesis alternativa. Aquí hay un ejemplo para demostrarlo.
Ejemplo\(\PageIndex{3}\) conclusion in hypothesis tests
En el sistema judicial estadounidense se podría establecer un juicio con jurado como prueba de hipótesis. Para ayudarte de verdad a ver cómo funciona esto, usemos como ejemplo OJ Simpson. En el sistema judicial se presume que una persona es inocente hasta que se demuestre su culpabilidad, y esta es tu nula hipótesis. OJ Simpson fue jugador de fútbol en la década de 1970. En 1994 su ex esposa y su amiga fueron asesinadas. OJ Simpson fue acusado del delito, y en 1995 se juzgó el caso. Los fiscales quisieron probar que OJ era culpable de matar a su esposa y a su amiga, y esa es la hipótesis alternativa
Solución
\(H_{0}\): OJ es inocente de matar a su esposa y a su amiga
\(H_{A}\): OJ es culpable de matar a su esposa y a su amiga
En este caso, se dictó sentencia de inocencia. Eso no quiere decir que sea inocente de este delito. Significa que no hubo pruebas suficientes para probar que era culpable. Mucha gente cree que OJ fue culpable de este delito, pero el jurado no consideró que las pruebas presentadas fueran suficientes para demostrar que había culpabilidad. ¡El veredicto en un juicio con jurado siempre es culpable o no culpable!
Lo mismo ocurre en una prueba de hipótesis. Hay evidencia suficiente o no suficiente para mostrar esa hipótesis alternativa. No es que haya demostrado que la hipótesis nula es cierta.
Al identificar hipótesis, es importante indicar tu variable aleatoria y el parámetro apropiado sobre el que quieres tomar una decisión. Si cuenta algo, entonces la variable aleatoria es el número de lo que sea que contaste. El parámetro es la proporción de lo que contaste. Si la variable aleatoria es algo que midió, entonces el parámetro es la media de lo que midió. (Nota: hay otros parámetros que puedes calcular, y algunos análisis de los mismos se presentarán en capítulos posteriores.)
Ejemplo\(\PageIndex{4}\) stating hypotheses
Identificar las hipótesis necesarias para probar las siguientes afirmaciones:
- El salario promedio de un maestro es de más de $30.000.
- La proporción de estudiantes que gustan de las matemáticas es menor al 10%.
- La edad promedio de los estudiantes en esta clase difiere de 21.
Solución
a. x = salario del profesor
\(\mu\)= salario medio del profesor
La conjetura es eso\(\mu>\$ 30,000\) y esa es la hipótesis alternativa.
La hipótesis nula tiene el mismo parámetro y número con un signo igual.
\(\begin{array}{l}{H_{0} : \mu=\$ 30,000} \\ {H_{A} : \mu>\$ 30,000}\end{array}\)
b. x = número de alumnos a los que les gustan las matemáticas
p = proporción de estudiantes a los que les gusta la matemática
La suposición es que p < 0.10 y esa es la hipótesis alternativa.
\(\begin{array}{l}{H_{0} : p=0.10} \\ {H_{A} : p<0.10}\end{array}\)
c. x = edad de los alumnos de esta clase
\(\mu\)= edad media de los estudiantes en esta clase
La conjetura es eso\(\mu \neq 21\) y esa es la hipótesis alternativa.
\(\begin{array}{c}{H_{0} : \mu=21} \\ {H_{A} : \mu \neq 21}\end{array}\)
Ejemplo\(\PageIndex{5}\) Stating Type I and II Errors and Picking Level of Significance
- El departamento de fitomejoramiento de una importante universidad desarrolló una nueva planta híbrida de frambuesa llamada YumYum Berry. Con base en datos de investigación, se afirma que a partir del momento en que se plantan los brotes se requieren 90 días en promedio para obtener la primera baya con una desviación estándar de 9.2 días. Una corporación interesada en comercializar el producto prueba 60 brotes plantándolos y registrando el número de días antes de que cada planta produzca su primera baya. La media muestral es de 92.3 días. La corporación quiere saber si el número medio de días es superior a los 90 días reclamados. Indicar los errores tipo I y tipo II en términos de este problema, las consecuencias de cada error y indicar qué nivel de significancia utilizar.
- En Australia se planteó la preocupación de que el porcentaje de muertes de presos aborígenes era superior al porcentaje de muertes de presos no indígenas, que es de 0.27%. Indicar los errores tipo I y tipo II en términos de este problema, las consecuencias de cada error y indicar qué nivel de significancia utilizar.
Solución
a. x = tiempo hasta la primera baya para la planta Yumyum Berry
\(\mu\)= tiempo medio hasta la primera baya para la planta Yumyum Berry
\(\begin{array}{l}{H_{0} : \mu=90} \\ {H_{A} : \mu>90}\end{array}\)
Tipo I Error: Si la corporación hace un error tipo I, entonces dirán que las plantas tardan más en producir que 90 días cuando no lo hacen Probablemente no querrán comercializar las plantas si piensan que tardarán más. No los comercializarán a pesar de que en realidad las plantas sí producen en 90 días. Pueden tener pérdida de ganancias futuras, pero eso es todo.
Error tipo II: La corporación no dice que las plantas tardan más de 90 días en producirse cuando sí tardan más. Lo más probable es que comercialicen las plantas. Las plantas tardarán más tiempo, por lo que los clientes podrían enojarse y luego la compañía obtendría mala reputación. Esto sería muy malo para la compañía.
Nivel de significación: Parece que la corporación no querría cometer un error tipo II. Elija un nivel de significancia del 10%,\(\alpha = 0.10\).
b. x = número de presos aborígenes fallecidos
p = proporción de presos aborígenes fallecidos
\(\begin{array}{l}{H_{o} : p=0.27 \%} \\ {H_{A} : p>0.27 \%}\end{array}\)
Error tipo I: Rechazando que la proporción de presos aborígenes fallecidos fue de 0.27%, cuando en realidad fue de 0.27%. Esto significaría que dirías que hay un problema cuando no hay uno. Podrías enojar a la comunidad aborigen, y dedicar tiempo y energía a investigar algo que no sea un problema.
Error tipo II: No rechazar que la proporción de presos aborígenes fallecidos fue de 0.27%, cuando en realidad es superior al 0.27%. Esto significaría que no pensarías que había un problema con que los prisioneros aborígenes murieran cuando realmente hay un problema. Te arriesgas a causar muertes cuando podría haber una manera de evitarlas.
Nivel de significación: Parece que ambos errores pueden ser cuestiones en este caso. No querrías enojar a la comunidad aborigen cuando no hay un problema, y no querrás que la gente muera cuando puede haber una manera de detenerlo. Puede ser mejor elegir un nivel de significación del 5%,\(\alpha = 0.05\).
Nota
La prueba de hipótesis es realmente fácil si sigues la misma receta cada vez. Las únicas diferencias en los diversos problemas son los supuestos de la prueba y el estadístico de prueba que calculas para que puedas encontrar el valor p. Hacer los mismos pasos, en el mismo orden, con las mismas palabras, cada vez y estos problemas se vuelven muy fáciles.
Testo
Ejercicio\(\PageIndex{1}\)
Por los problemas de esta sección, se está formulando una pregunta. Esto es para ayudarte a entender cuáles son las hipótesis. No debes ejecutar ninguna prueba de hipótesis y llegar a ninguna conclusión en esta sección.
- Eyeglassomatic fabrica anteojos para diferentes minoristas. Prueban para ver cuántas lentes defectuosas fabricaron en un periodo de tiempo determinado y encontraron que el 11% de todas las lentes tenían defectos de algún tipo. Al observar el tipo de defectos, encontraron en un periodo de tiempo de tres meses que de 34,641 lentes defectuosas, 5865 fueron por rasguños. ¿Hay más defectos por arañazos que por todas las demás causas? Indicar la variable aleatoria, el parámetro poblacional y las hipótesis.
- Según el informe de la Comisión Federal de Comercio de febrero de 2008 sobre fraude al consumidor y robo de identidad, 23% de todas las denuncias en 2007 fueron por robo de identidad. En ese año, Alaska tenía 321 denuncias de robo de identidad de un total de 1,432 quejas de consumidores (“Fraude al consumidor y”, 2008). ¿Estos datos proporcionan evidencia suficiente para mostrar que Alaska tuvo una proporción menor de robo de identidad que 23%? Indicar la variable aleatoria, el parámetro poblacional y las hipótesis.
- El Protocolo de Kyoto se firmó en 1997, y requería que los países comenzaran a reducir sus emisiones de carbono. El protocolo se hizo exigible en febrero de 2005. En 2004, la emisión media de CO2 fue de 4.87 toneladas métricas per cápita. ¿Existe evidencia suficiente para demostrar que la emisión media de CO2 es menor en 2010 que en 2004? Indicar la variable aleatoria, el parámetro poblacional y las hipótesis.
- La FDA regula que el pescado que se consume pueda contener 1.0 mg/kg de mercurio. En Florida, se recolectaron peces lubinos en 53 lagos diferentes para medir la cantidad de mercurio en los peces. Los datos para la cantidad promedio de mercurio en cada lago se encuentran en Ejemplo\(\PageIndex{5}\) (“Actividad multidisciplinaria de niser”, 2013). ¿Los datos proporcionan evidencia suficiente para mostrar que los peces en los lagos de Florida tienen más mercurio que la cantidad permitida? Indicar la variable aleatoria, el parámetro poblacional y las hipótesis.
- Eyeglassomatic fabrica anteojos para diferentes minoristas. Prueban para ver cuántas lentes defectuosas fabricaron en un periodo de tiempo determinado y encontraron que el 11% de todas las lentes tenían defectos de algún tipo. Al observar el tipo de defectos, encontraron en un periodo de tiempo de tres meses que de 34,641 lentes defectuosas, 5865 fueron por rasguños. ¿Hay más defectos por arañazos que por todas las demás causas? Indicar los errores tipo I y tipo II en este caso, consecuencias de cada tipo de error para esta situación desde la perspectiva del fabricante, y el nivel alfa apropiado a utilizar. Indica por qué elegiste este nivel alfa.
- Según el informe de la Comisión Federal de Comercio de febrero de 2008 sobre fraude al consumidor y robo de identidad, 23% de todas las denuncias en 2007 fueron por robo de identidad. En ese año, Alaska tenía 321 denuncias de robo de identidad de un total de 1,432 quejas de consumidores (“Fraude al consumidor y”, 2008). ¿Estos datos proporcionan evidencia suficiente para mostrar que Alaska tuvo una proporción menor de robo de identidad que 23%? Indicar los errores tipo I y tipo II en este caso, las consecuencias de cada tipo de error para esta situación desde la perspectiva del estado de Arizona, y el nivel alfa apropiado a utilizar. Indica por qué elegiste este nivel alfa.
- El Protocolo de Kyoto se firmó en 1997, y requería que los países comenzaran a reducir sus emisiones de carbono. El protocolo se hizo exigible en febrero de 2005. En 2004, la emisión media de CO2 fue de 4.87 toneladas métricas per cápita. ¿Existe evidencia suficiente para demostrar que la emisión media de CO2 es menor en 2010 que en 2004? Indicar los errores tipo I y tipo II en este caso, las consecuencias de cada tipo de error para esta situación desde la perspectiva del organismo que supervisa el protocolo, y el nivel alfa apropiado a utilizar. Indica por qué elegiste este nivel alfa.
- La FDA regula que el pescado que se consume pueda contener 1.0 mg/kg de mercurio. En Florida, se recolectaron peces lubinos en 53 lagos diferentes para medir la cantidad de mercurio en los peces. Los datos para la cantidad promedio de mercurio en cada lago se encuentran en Ejemplo\(\PageIndex{5}\) (“Actividad multidisciplinaria de niser”, 2013). ¿Los datos proporcionan evidencia suficiente para mostrar que los peces en los lagos de Florida tienen más mercurio que la cantidad permitida? Indicar los errores tipo I y tipo II en este caso, las consecuencias de cada tipo de error para esta situación desde la perspectiva de la FDA, y el nivel alfa apropiado a utilizar. Indica por qué elegiste este nivel alfa.
- Contestar
-
1. \(H_{o} : p=0.11, H_{A} : p>0.11\)
3. \(H_{o} : \mu=4.87 \text { metric tons per capita, } H_{A} : \mu<4.87 \text { metric tons per capita }\)
5. Ver soluciones
7. Ver soluciones


