Saltar al contenido principal
LibreTexts Español

7.3: Prueba de una muestra para la media

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    149733

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Es momento de volver a mirar la prueba para la media que se introdujo en la sección 7.1 llamada prueba z. En el ejemplo, sabías cuál era la desviación estándar poblacional\(\sigma\),,. ¿Y si no lo sabes\(\sigma\)?

    Simplemente podría usar la desviación estándar de la muestra, s, como una aproximación de\(\sigma\). Eso significa que el estadístico de prueba es ahora\(\dfrac{\overline{x}-\mu}{s / \sqrt{n}}\). Genial, ahora puedes ir y encontrar el valor p usando la curva normal. ¿O puedes? ¿Este nuevo estadístico de prueba se distribuye normalmente? En realidad, no lo es. ¿Cómo se distribuye? Un hombre llamado W. S. Gossett descubrió lo que es esta distribución y la llamó la distribución t de Student. Hay algunos supuestos que deben hacerse para que esta fórmula sea una distribución t de Student. Estos se describen en el siguiente teorema. Nota: la distribución t se llama distribución t del Estudiante porque ese es el nombre con el que publicó porque no pudo publicar bajo su propio nombre debido a que el empleador no quería que publicara bajo su propio nombre. Su patrón por cierto era Guinness y no querían que los competidores supieran que tenían un químico trabajando para ellos. No se llama la distribución t del Estudiante porque solo es utilizada por los estudiantes.

    Teorema: Si se cumplen los siguientes supuestos

    1. Se toma una muestra aleatoria de tamaño n.
    2. La distribución de la variable aleatoria es normal o el tamaño de la muestra es 30 o más.

    Entonces la distribución de\(t=\dfrac{\overline{x}-\mu}{s / \sqrt{n}}\) es una distribución t de Student con\(n-1\) grados de libertad.

    Explicación de grados de libertad:

    Recordemos la fórmula para la desviación estándar de la muestra es\(s=\sqrt{\dfrac{\sum(x-\overline{x})^{2}}{n-1}}\). Observe que el denominador es n - 1. Esto es lo mismo que los grados de libertad. Esto no es un accidente. La razón por la que el denominador y los grados de libertad son ambos n -1 proviene de cómo se calcula la desviación estándar. Recuerda, primero tomas cada valor de datos y restas\(\overline{x}\). Si suma todos estos nuevos valores, obtendrá 0. Esto debe suceder. Ya que debe suceder, los primeros valores de datos n - 1 tienes “libertad de elección”, pero el enésimo valor de datos, no tienes libertad para elegir. De ahí que tengas n - 1 grados de libertad. Otra forma de pensarlo es que si ustedes cinco personas y cinco sillas, las primeras cuatro personas tienen la opción de dónde están sentadas, pero la última persona no. No tienen libertad de dónde sentarse. Sólo 5 - 1 =4 personas tienen libertad de elección.

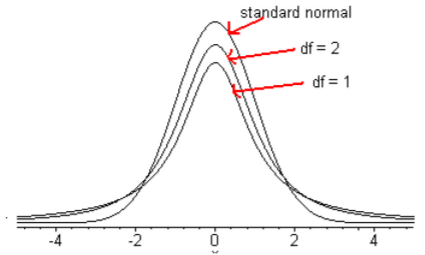
    La distribución t de Student es una forma de campana que está más extendida que la distribución normal. Hay muchas distribuciones t, una para cada grado diferente de libertad.

    Aquí hay una gráfica de la distribución normal y la distribución t de Student para df = 1 y df = 2.

    Captura de pantalla (142) .png
    Figura\(\PageIndex{1}\): Distribuciones T típicas de estudiantes

    A medida que aumentan los grados de libertad, la distribución t del estudiante se parece más a la distribución normal.

    Para encontrar probabilidades para la distribución t, nuevamente la tecnología puede hacer esto por usted. Hay muchas tecnologías por ahí que puedes usar. En el TI-83/84, el comando se encuentra en el menú DISTR/MOL y es tcdf (. La sintaxis de este comando es

    tcdf (límite inferior, límite superior, df)

    En R: el comando para encontrar el área a la izquierda de un valor t es pt (valor t, df)

    Prueba de hipótesis para una media poblacional (prueba T)

    1. Indicar la variable aleatoria y el parámetro en palabras.
      x = variable aleatoria
      \(\mu\) = media de la variable aleatoria
    2. Indique las hipótesis nulas y alternativas y el nivel de significación
      \(H_{o} : \mu=\mu_{o}\), donde\(\mu_{o}\) está la media conocida
      \(H_{A} : \mu<\mu_{o}\)
      \(H_{A} : \mu>\mu_{o}\), use la apropiada para su problema
      \(H_{A} : \mu \neq \mu_{o}\)
      También, indique su \(\alpha\)nivel aquí.
    3. Indicar y verificar los supuestos para una prueba de hipótesis
      1. Se toma una muestra aleatoria de tamaño n.
      2. La población de la variable aleatoria se distribuye normalmente, aunque la prueba t es bastante robusta a la condición si el tamaño de la muestra es grande. Esto significa que si no se cumple esta condición, pero el tamaño de su muestra es bastante grande (más de 30), entonces los resultados de la prueba t son válidos.
      3. Se desconoce la desviación estándar poblacional\(\sigma\),,.
    4. Encuentre el estadístico de muestra, el estadístico de prueba y el valor p Estadístico de
      prueba:
      \(t=\dfrac{\overline{x}-\mu}{\dfrac{s}{\sqrt{n}}}\)
      con grados de libertad df = n - 1
      valor p:
      Usando TI-83/84: tcdf (límite inferior, límite superior, df)

      Nota

      Si\(H_{A} : \mu<\mu_{o}\), entonces el límite inferior es\(-1 E 99\) y el límite superior es su estadística de prueba. Si\(H_{A} : \mu>\mu_{o}\), entonces el límite inferior es su estadística de prueba y el límite superior es\(1 E 99\). Si\(H_{A} : \mu \neq \mu_{o}\), entonces encuentra el valor p para\(H_{A} : \mu<\mu_{o}\), y multiplica por 2.

      Usando R: pt (valor t, df)

      Nota

      Si\(H_{A} : \mu<\mu_{o}\), entonces el comando es pt (t value, df). Si\(H_{A} : \mu>\mu_{o}\), entonces el comando es\(1- \text {pt(t value, df })\). Si\(H_{A} : \mu \neq \mu_{o}\), entonces encuentra el valor p para\(H_{A} : \mu<\mu_{o}\), y multiplica por 2.

    5. Aquí es donde escribes rechazar\(H_{o}\) o no rechazar\(H_{o}\). La regla es: si el valor p <\(\alpha\), entonces rechazar\(H_{o}\). Si el valor p\(\geq \alpha\), entonces no puede rechazar\(H_{o}\).
    6. Aquí es donde interpretas en términos del mundo real la conclusión a la prueba. La conclusión para una prueba de hipótesis es que o bien tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad, o no tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad.

    Cómo verificar los supuestos de la prueba t:

    Para que la prueba t sea válida, los supuestos de la prueba deben ser ciertos. Siempre que ejecutes una prueba t, debes asegurarte de que los supuestos sean ciertos. Es necesario que los revises. Así es como haces esto:

    1. Para la condición de que la muestra sea una muestra aleatoria, describa cómo tomó la muestra. Asegúrate de que tu técnica de muestreo sea aleatoria.
    2. Para la condición de que la población de la variable aleatoria sea normal, recuerde el proceso de evaluación de la normalidad a partir del capítulo 6.

    Nota

    Si los supuestos detrás de esta prueba no son válidos, entonces las conclusiones que hagas de la prueba no son válidas. Si no tienes una muestra aleatoria, es tu culpa. Asegúrate de que la muestra que tomes sea tan aleatoria como puedas hacerla siguiendo las técnicas de muestreo del capítulo 1. Si la población de la variable aleatoria no es normal, entonces toma una muestra mayor a 30. Si no puedes permitirte hacer eso, o si no es logísticamente posible, entonces haces diferentes pruebas llamadas pruebas no paramétricas. Hay un curso completo sobre pruebas no paramétricas, y no serán discutidas en este libro.

    Ejemplo\(\PageIndex{1}\) test of the mean using the formula

    Se tomó una muestra aleatoria de 20 puntajes de coeficiente intelectual de personajes famosos del sitio web de IQ of Famous People (“IQ of Famous”, 2013) y se utilizó un generador de números aleatorios para escoger 20 de ellos. Los datos están en Ejemplo\(\PageIndex{1}\). ¿Los datos proporcionan evidencia al nivel del 5% de que el coeficiente intelectual de una persona famosa es superior al coeficiente intelectual promedio de 100?

    158 180 150 137 109
    225 122 138 145 180
    118 118 126 140 165
    150 170 105 154 118
    Tabla\(\PageIndex{1}\): Puntajes de coeficiente intelectual de personajes famosos
    1. Indicar la variable aleatoria y el parámetro en palabras.
    2. Indicar las hipótesis nulas y alternativas y el nivel de significación.
    3. Indicar y verificar los supuestos para una prueba de hipótesis.
    4. Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
    5. Conclusión
    6. Interpretación

    Solución

    1. x = Puntuación de coeficiente intelectual de una persona famosa

    \(\mu\)= puntuación media de coeficiente intelectual de una persona famosa

    2. \(\begin{array}{l}{H_{o} : \mu=100} \\ {H_{A} : \mu>100} \\ {\alpha=0.05}\end{array}\)

    3.

    1. Se tomó una muestra aleatoria de 20 puntajes de CI. Esto se dijo en el problema.
    2. La población de puntaje de CI se distribuye normalmente. Esto se mostró en Ejemplo\(\PageIndex{2}\).

    4. Estadística de muestra:

    \(\begin{array}{l}{\overline{x}=145.4} \\ {s \approx 29.27}\end{array}\)

    Estadística de prueba:

    \(t=\dfrac{\overline{x}-\mu}{\dfrac{s}{\sqrt{n}}}=\dfrac{145.4-100}{\dfrac{29.27}{\sqrt{20}}} \approx 6.937\)

    valor p:

    df = n - 1 = 20 - 1 = 19

    TI-83/84: valor p =\(\operatorname{tcdf}(6.937,1 E 99,19)=6.5 \times 10^{-7}\)

    R: valor p =\(1-\text{pt}(6.937,19)=6.5 \times 10^{-7}\)

    5. Dado que el valor p es menor al 5%, entonces rechace\(H_{o}\).

    6. Hay pruebas suficientes para demostrar que las personas famosas tienen un coeficiente intelectual más alto que el coeficiente intelectual promedio de 100.

    Ejemplo\(\PageIndex{2}\) test of the mean using technology

    En 2011, la esperanza de vida promedio de una mujer en Europa era de 79.8 años. Los datos en Ejemplo\(\PageIndex{2}\) son las expectativas de vida de los hombres en los países europeos en 2011 (“Esperanza de vida de la OMS”, 2013). ¿Los datos indican que la esperanza de vida de los hombres es menor que la de las mujeres? Prueba al nivel 1%.

     Tabla\(\PageIndex{2}\): Esperanza de vida de los hombres en países europeos en 2011
    1. Indicar la variable aleatoria y el parámetro en palabras.
    2. Indicar las hipótesis nulas y alternativas y el nivel de significación.
    3. Indicar y verificar los supuestos para una prueba de hipótesis.
    4. Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
    5. Conclusión
    6. Interpretación

    Solución

    1. x = esperanza de vida de un hombre europeo en 2011

    \(\mu\)= esperanza de vida media de los hombres europeos en 2011

    2. \(\begin{array}{l}{H_{o} : \mu=79.8 \text { years }} \\ {H_{A} : \mu<79.8 \text { years }} \\ {\alpha=0.01}\end{array}\)

    3.

    1. Se tomó una muestra aleatoria de 53 expectativas de vida de hombres europeos en 2011. Los datos son en realidad todas las expectativas de vida de cada país que es considerado parte de Europa por la Organización Mundial de la Salud. Sin embargo, la información sigue siendo información de muestra ya que es solo por un año que se recopilaron los datos. Puede que no sea una muestra aleatoria, pero eso probablemente no sea un problema en este caso.
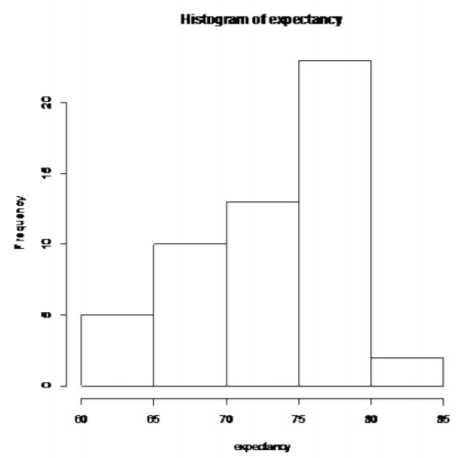
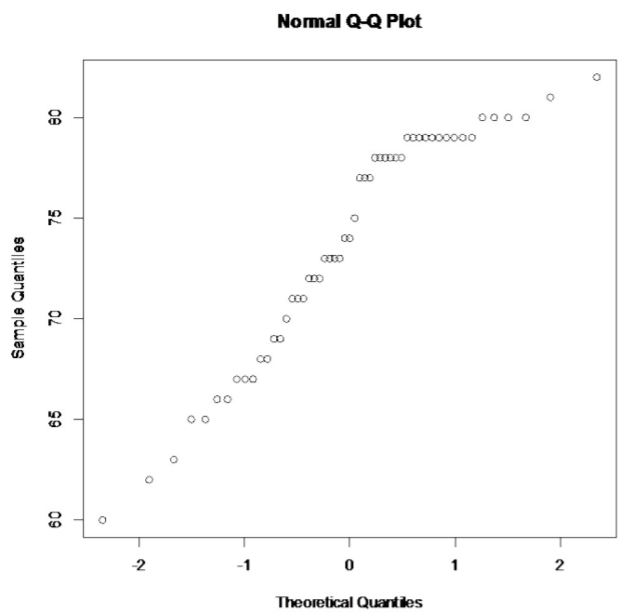
    2. La distribución de la esperanza de vida de los hombres europeos en 2011 se distribuye normalmente. Para ver si se ha cumplido esta condición, observe el histograma, el número de valores atípicos y la gráfica de probabilidad normal. (Si lo desea, puede mirar primero la gráfica de probabilidad normal. Si no se ve lineal, entonces es posible que desee mirar el histograma y el número de valores atípicos en este punto).
    Captura de pantalla (143) .png
    Figura\(\PageIndex{2}\): Histograma de esperanza de vida de hombres europeos en 2011

    No en forma de campana

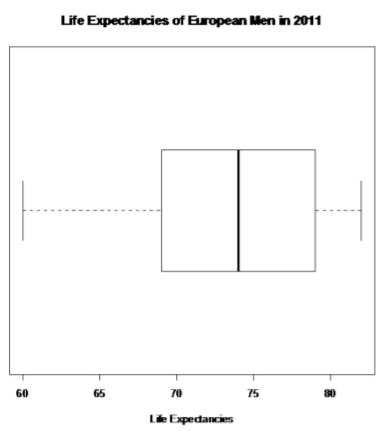
    Número de valores atípicos:

    Captura de pantalla (144) .png
    Figura\(\PageIndex{3}\): Gráfica de caja modificada para la esperanza de vida de hombres europeos en 2011

    o:

    IQR = 79 - 69 = 10

    1.5 * IQR = 15

    Q 1 - 1.5 * IQR = 69 - 15 = 54

    Q 3 + 1.5 * IQR = 79 + 15 = 94

    Los valores atípicos son números por debajo del 54 y por encima del 94. No hay valores atípicos para este conjunto de datos.

    Captura de pantalla (145) .png
    Figura\(\PageIndex{4}\): Gráfica de cuantiles normales para la esperanza de vida de hombres europeos en 2011

    No lineal

    Esta población no parece estar normalmente distribuida. Esta muestra es mayor a 30, por lo que es bueno que la prueba t sea robusta.

    4. Los cálculos se realizarán utilizando tecnología.

    En la calculadora TI-83/84. Vaya a STAT y escriba los datos en L1.

    Después entra en STAT y pasa a PRUEBAS. Elija T-Test. La configuración de la calculadora está en la Figura\(\PageIndex{4}\).

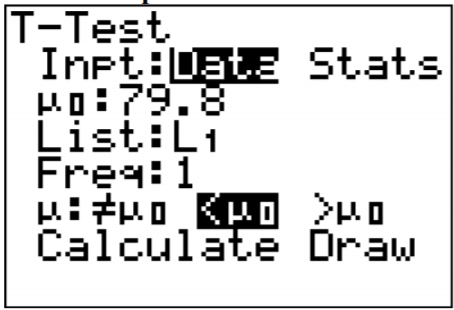    Captura de pantalla (146) .png
    Figura\(\PageIndex{5}\): Configuración para la prueba T en la calculadora TI-83/84

    Una vez que presione ENTRAR en Calcular verá el resultado que se muestra en la Figura\(\PageIndex{6}\).

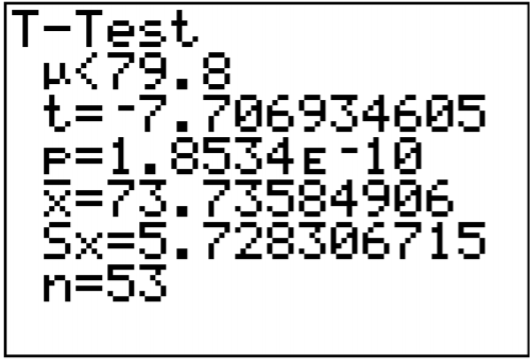    Captura de pantalla (147) .png
    Figura\(\PageIndex{6}\): Resultado de la prueba T en la calculadora TI-83/84

    En R, el comando es t.test (variable, mu = número en\(\mathrm{H}_{0}\), alternativa = “menos” o “mayor”), donde mu = lo\(\mathrm{H}_{0}\) que dice la media es igual, y usas menos si tu\(\mathrm{H}_{A}\) es menor y mayor si tu\(\mathrm{H}_{A}\) es mayor. Si tu no\(\mathrm{H}_{A}\) es igual a, entonces deja fuera la declaración alternativa. Para este ejemplo, el comando sería t.test (expectativa, mu=79.8, alternativa = “menos”)

    Prueba t de una muestra

    data: expectativa

    t = -7.7069, df = 52, valor p = 1.853e-10

    hipótesis alternativa: la media verdadera es menor que 79.8

    Intervalo de confianza del 95 por ciento:

    -Inf 75.05357

    estimaciones de muestra:

    media de x

    73.73585

    La mayor parte de la salida no necesitas. Necesitas el estadístico de prueba y el valor p.

    El t = -7.707 es el estadístico de prueba. El valor p es\(1.8534 \times 10^{-10}\).

    5. Dado que el valor p es menor al 1%, entonces rechace\(H_{o}\).

    6. Existe evidencia suficiente para demostrar que la esperanza de vida media para los hombres europeos en 2011 fue menor que la esperanza de vida media de las mujeres europeas en 2011 de 79.8 años.

    Testo

    Ejercicio\(\PageIndex{1}\)

    En cada problema se muestran todos los pasos de la prueba de hipótesis. Si no se cumplen algunos de los supuestos, tenga en cuenta que los resultados de la prueba pueden no ser correctos y luego continuar el proceso de la prueba de hipótesis.

    1. El Protocolo de Kyoto se firmó en 1997, y requería que los países comenzaran a reducir sus emisiones de carbono. El protocolo se hizo exigible en febrero de 2005. En 2004, la emisión media de CO2 fue de 4.87 toneladas métricas per cápita. La tabla\(\PageIndex{3}\) contiene una muestra aleatoria de emisiones de CO2 en 2010 (“emisiones de CO2”, 2013). ¿Existe evidencia suficiente para demostrar que la emisión media de CO2 es menor en 2010 que en 2004? Prueba al nivel 1%.
      1.36 1.42 5.93 5.36 0.06 9.11 7.32
      7.93 6.72 0.78 1.80 0.20 2.27 0.28
      5.86 3.46 1.46 0.14 2.62 0.79 7.48
      0.86 7.84 2.87 2.45
      Tabla\(\PageIndex{3}\): Emisiones de CO2 (en toneladas métricas per cápita) en 2010
    2. La cantidad de azúcar en una donut glaseada Krispy Kream es de 10 g. Muchas personas sienten que el cereal es una alternativa más saludable para los niños sobre las donas glaseadas. Ejemplo\(\PageIndex{4}\) contiene la cantidad de azúcar en una muestra de cereal que está dirigida a los niños (“Healthy breakfast story”, 2013). ¿Hay pruebas suficientes para demostrar que la cantidad media de azúcar en el cereal infantil es mayor que en una dona glaseada? Prueba al nivel del 5%.

      10 14 12 9 13 13 13
      11 12 15 9 10 11 3
      6 12 15 12 12
      Tabla\(\PageIndex{4}\): Cantidades de Azúcar en Cereales Infantiles
    3. La FDA regula que el pescado que se consume pueda contener 1.0 mg/kg de mercurio. En Florida, se recolectaron peces lubinos en 53 lagos diferentes para medir la cantidad de mercurio en los peces. Los datos para la cantidad promedio de mercurio en cada lago se encuentran en Ejemplo\(\PageIndex{5}\) (“Actividad multidisciplinaria de niser”, 2013). ¿Los datos proporcionan evidencia suficiente para mostrar que los peces en los lagos de Florida tienen más mercurio que la cantidad permitida? Prueba al nivel del 10%.

      1.23 1.33 0.04 0.44 1.20 0.27
      0.48 0.19 0.83 0.81 0.81 0.5
      0.49 1.16 0.05 0.15 0.19 0.77
      1.08 0.98 0.63 0.56 0.41 0.73
      0.34 0.59 0.34 0.84 0.50 0.34
      0.28 0.34 0.87 0.56 0.17 0.18
      0.19 0.04 0.49 1.10 0.16 0.10
      0.48 0.21 0.86 0.52 0.65 0.27
      0.94 0.40 0.43 0.25 0.27
      Tabla\(\PageIndex{5}\): Niveles promedio de mercurio (mg/kg) en peces
    4. Stephen Stigler determinó en 1977 que la velocidad de la luz es de 299,710.5 km/seg. En 1882, Albert Michelson había recolectado mediciones sobre la velocidad de la luz (“Student t-distribution”, 2013). Sus medidas se dan en Ejemplo\(\PageIndex{6}\). ¿Hay evidencia que demuestre que los datos de Michelson son diferentes del valor de Stigler de la velocidad de la luz? Prueba al nivel del 5%.

      299883 299816 299778 299796 299682
      299711 299611 299599 300051 299781
      299578 299796 299774 299820 299772
      299696 299573 299748 299748 299797
      299851 299809 299723
      Tabla\(\PageIndex{6}\): Velocidad de las mediciones de la luz en (km/seg)
    5. Ejemplo\(\PageIndex{7}\) contiene frecuencias de pulso después de correr por 1 minuto, recolectadas de hembras que beben alcohol (“Pulso antes”, 2013). La frecuencia media del pulso después de correr por 1 minuto de las hembras que no beben es de 97 latidos por minuto. ¿Los datos muestran que la frecuencia media del pulso de las hembras que sí beben alcohol es mayor que la frecuencia media del pulso de las hembras que no beben? Prueba al nivel del 5%.

      176 150 150 115 129 160
      120 125 89 132 120 120
      68 87 88 72 77 84
      92 80 60 67 59 64
      88 74 68
      Tabla\(\PageIndex{7}\): Pulso de mujeres que consumen alcohol
    6. El dinamismo económico, que es el índice de crecimiento productivo en dólares para los países que son designados por el Banco Mundial como de ingresos medios se encuentran en Ejemplo\(\PageIndex{8}\) (“Datos SOCR 2008,” 2013). Los países que se consideran de ingresos altos tienen un dinamismo económico medio de 60.29. ¿Los datos muestran que el dinamismo económico medio de los países de ingresos medios es menor que la media de los países de ingresos altos? Prueba al nivel del 5%.

      25.8057 37.4511 51.915 43.6952 47.8506 43.7178 58.0767
      41.1648 38.0793 37.7251 39.6553 42.0265 48.6159 43.8555
      49.1361 61.9281 41.9543 44.9346 46.0521 48.3652 43.6252
      50.9866 59.1724 39.6282 33.6074 21.6643
      Tabla\(\PageIndex{8}\): Dinamismo económico de los países de renta media
    7. En 1999, el porcentaje promedio de mujeres que recibieron atención prenatal por país es de 80,1%. Ejemplo\(\PageIndex{9}\) contiene el porcentaje de mujeres que recibieron atención prenatal en 2009 para una muestra de países (“Mujer embarazada que recibe”, 2013). ¿Los datos muestran que el porcentaje promedio de mujeres que recibieron atención prenatal en 2009 es mayor que en 1999? Prueba al nivel del 5%.

      70.08 72.73 74.52 75.79 76.28 76.28
      76.65 80.34 80.60 81.90 86.30 87.70
      87.76 88.40 90.70 91.50 91.80 92.10
      92.20 92.41 92.47 93.00 93.20 93.40
      93.63 93.69 93.80 94.30 94.51 95.00
      95.80 95.80 96.23 96.24 97.30 97.90
      97.95 98.20 99.00 99.00 99.10 99.10
      100.00 100.00 100.00 100.00 100.00
      Tabla\(\PageIndex{9}\): Porcentaje de mujeres que reciben atención prenatal
    8. Mantener el equilibrio puede ser más difícil a medida que envejece. Se realizó un estudio para ver qué tan estable es el adulto mayor sobre sus pies. Tenían a los sujetos parados sobre una plataforma de fuerza y hacerlos reaccionar ante un ruido. La plataforma de fuerza entonces midió cuánto se balanceaban hacia adelante y hacia atrás, y los datos están en Ejemplo\(\PageIndex{10}\) (“Mantener el equilibrio mientras”, 2013). ¿Los datos muestran que los adultos mayores se balancean más que el balanceo medio hacia adelante de los jóvenes, que es de 18.125 mm? Prueba al nivel del 5%.

      19 30 20 19 29 25 21 24 50
      Tabla\(\PageIndex{10}\): Balanceo hacia adelante/atrás (en mm) de sujetos de edad avanzada
    Responder

    Para todas las pruebas de hipótesis, solo se da la conclusión. Ver soluciones para toda la respuesta.

    1. No rechazar a Ho.

    3. No rechazar a Ho.

    5. No rechazar a Ho.

    7. Rechazar Ho.

    Fuentes de datos:

    Comisión Australiana de Derechos Humanos, (1996). Muertes indígenas bajo custodia 1989 - 1996. Recuperado del sitio web: www.humanrights.gov.au/public... deaths-custody

    Características de los CDC: nuevos datos sobre trastornos del espectro autista. (2013, 26 de noviembre). Recuperado a partir de www.cdc.gov/features/countingautism/

    Centro de Control y Prevención de Enfermedades, Prevalencia de Trastornos del Espectro Autista - Red de Monitoreo del Autismo y Discapacidades del Desarrollo. (2008 Red de monitoreo de autismo y discapacidades del desarrollo-2012. Recuperado del sitio web: www.cdc.gov/ncbddd/autism/doc... nityReport.pdf

    Emisiones de CO2. (2013, 19 de noviembre). Recuperado a partir de http://data.worldbank.org/indicator/EN.ATM.CO2E.PC

    Comisión Federal de Comercio, (2008). Datos de denuncia por fraude al consumidor y robo de identidad: enero-diciembre de 2007. Recuperado del sitio web: www.ftc.gov/opa/2008/02/fraud.pdf

    Servicio de noticias Gallup. (2013, 7 al 10 de noviembre). Recuperado a partir de www.gallup.com/file/poll/1658... acy_131115.pdf

    Historia del desayuno saludable. (2013, 16 de noviembre). Recuperado de lib.stat.cmu.edu/dasl/stories... Breakfast.html

    CI de personajes famosos. (2013, 13 de noviembre). Recuperado a partir de http://www.kidsiqtestcenter.com/IQ-famous-people.html

    Mantener el equilibrio mientras se concentra. (2013, 25 de septiembre). Recuperado a partir de http://www.statsci.org/data/general/balaconc.html

    Encuesta de Morgan Gallup sobre desempleo. (2013, 26 de septiembre). Recuperado a partir de http://www.statsci.org/data/oz/gallup.html

    Actividad multidisciplinaria de niser - mercurio en el bajo. (2013, 16 de noviembre). Recuperado de http://gozips.uakron.edu/~nmimoto/pa... /MercuryInBass - description.txt

    Mujer embarazada que recibe atención prenatal. (2013, 14 de octubre). Recuperado a partir de http://data.worldbank.org/indicator/SH.STA.ANVC.ZS

    Datos SOCR 2008 rankings mundiales de países. (2013, 16 de noviembre). Recuperado a partir de http://wiki.stat.ucla.edu/socr/index...ntriesRankings

    T-distribución estudiantil. (2013, 25 de noviembre). Recuperado de lib.stat.cmu.edu/dasl/Stories/Student.html

    Esperanza de vida de la OMS. (2013, 19 de septiembre). Recuperado de www.who.int/gho/mortality_bur... n_trends/es/en dex.html

    This page titled 7.3: Prueba de una muestra para la media is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Kathryn Kozak via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.