Saltar al contenido principal
LibreTexts Español

9.1: Dos proporciones

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    149708

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Hay momentos en los que se quiere probar un reclamo sobre dos proporciones de población o construir una estimación de intervalo de confianza de la diferencia entre dos proporciones de población. Al igual que con todas las demás pruebas de hipótesis e intervalos de confianza, el proceso es el mismo aunque las fórmulas y suposiciones son diferentes.

    Prueba de hipótesis para la proporción de dos poblaciones (prueba 2-prop)

    1. Indicar las variables aleatorias y los parámetros en palabras.
      \(x_{1}\)= número de éxitos del grupo 1
      \(x_{2}\) = número de éxitos del grupo 2
      \(p_{1}\) = proporción de éxitos en el grupo 1
      \(p_{2}\) = proporción de éxitos en el grupo 2
    2. Indique las hipótesis nulas y alternativas y el nivel de significación
      \(\begin{array}{ll}{H_{o} : p_{1}=p_{2}} & {\text { or } \quad H_{o} : p_{1}-p_{2}=0} \\ {H_{A} : p_{1}<p_{2}} &\quad\quad\: {H_{A} : p_{1}-p_{2}<0} \\ {H_{A} : p_{1}>p_{2}} &\quad\quad\: {H_{A} : p_{1}-p_{2}>0} \\ {H_{A} : p_{1} \neq p_{2}} & \quad\quad\:{H_{A} : p_{1}-p_{2} \neq 0}\end{array}\)
      También, indique aquí su\(\alpha\) nivel.
    3. Indicar y verificar los supuestos para una prueba de hipótesis
      1. \(n_{1}\)Se toma una muestra aleatoria simple de tamaño de la población 1, y una muestra aleatoria simple de tamaño\(n_{2}\) se toma de la población 2.
      2. Las muestras son independientes.
      3. Los supuestos para la distribución binomial se satisfacen para ambas poblaciones.
      4. Para determinar la distribución de muestreo de\(\hat{p}_{1}\), es necesario mostrar eso\(n_{1} p_{1} \geq 5\) y\(n_{1} q_{1} \geq 5\), dónde\(q_{1}=1-p_{1}\). Si este requisito es cierto, entonces la distribución de muestreo de\(\hat{p}_{1}\) es bien aproximada por una curva normal. Para determinar la distribución de muestreo de\(\hat{p}_{2}\), es necesario mostrar eso\(n_{2} p_{2} \geq 5\) y\(n_{2} q_{2} \geq 5\), dónde\(q_{2}=1-p_{2}\). Si este requisito es cierto, entonces la distribución de muestreo de\(\hat{p}_{2}\) es bien aproximada por una curva normal. Sin embargo, no lo sabes\(p_{1}\) y\(p_{2}\), entonces necesitas usar\(\hat{p}_{1}\) y en su lugar\(\hat{p}_{2}\). Esto no es perfecto, pero es lo mejor que puedes hacer. Ya que\(n_{1} \hat{p}_{1}=n_{1} \dfrac{x_{1}}{n_{1}}=x_{1}\) (y similares para los otros cálculos) solo necesitas asegurarte de que\(x_{1}\),\(n_{1}-x_{1}\),\(n_{2}-x_{2}\), y son todos más de 5.
    4. Encuentre los estadísticos de muestra, el estadístico de prueba y el valor p Proporción de
      muestra: Proporción de muestra
      \(\begin{array}{ll}{n_{1}=\text { size of sample } 1} & {n_{2}=\text { size of sample } 2} \\ {\hat{p}_{1}=\dfrac{x_{1}}{n_{1}}(\text { sample } 1 \text { proportion) }} & {\hat{p}_{2}=\dfrac{x_{2}}{n_{2}} \text { (sample } 2 \text { proportion) }} \\ {\hat{q}_{1}=1-\hat{p}_{1} \text { (complement of } \hat{p}_{1} )} & {\hat{q}_{2}=1-\hat{p}_{2} \text { (complement of } \hat{p}_{2} )}\end{array}\)
      agrupada,\(\overline{p}\): Estadística de
      \(\begin{aligned} \overline{p} &=\dfrac{x_{1}+x_{2}}{n_{1}+n_{2}} \\ \overline{q} &=1-\overline{p} \end{aligned}\)
      prueba:
      \(z=\dfrac{\left(\hat{p}_{1}-\hat{p}_{2}\right)-\left(p_{1}-p_{2}\right)}{\sqrt{\dfrac{\overline{p} \overline{q}}{n_{1}}+\dfrac{\overline{p} \overline{q}}{n_{2}}}}\)
      Generalmente \(p_{1} - p_{2} = 0\), ya que el\(H_{o} : p_{1}=p_{2}\)
      valor p: En TI-83/84: use normalcdf (límite inferior, límite superior, 0, 1)

      Nota

      Si\(H_{A} : p_{1}<p_{2}\) entonces el límite inferior es\(-1 E 99\) y el límite superior es su estadística de prueba. Si\(H_{A} : p_{1}>p_{2}\), entonces el límite inferior es su estadística de prueba y el límite superior es\(1 E 99\). Si\(H_{A} : p_{1} \neq p_{2}\), entonces encuentra el valor p para\(H_{A} : p_{1}<p_{2}\), y multiplica por 2.

      En R: use pnorm (z, 0, 1)

      Nota

      Si\(H_{A} : p_{1}<p_{2}\), entonces usa pnorm (z, 0, 1). Si\(H_{A} : p_{1}>p_{2}\), entonces usa 1 - pnorm (z, 0, 1). Si\(H_{A} : p_{1} \neq p_{2}\), entonces encuentra el valor p para\(H_{A} : p_{1}<p_{2}\), y multiplica por 2.

    5. Conclusión Aquí es donde escribes rechazar\(H_{o}\) o no rechazar\(H_{o}\). La regla es: si el valor p <\(\alpha\), entonces rechazar\(H_{o}\). Si el valor p\(\geq \alpha\), entonces no puede rechazar\(H_{o}\).
    6. Interpretación Aquí es donde interpretas en términos del mundo real la conclusión a la prueba. La conclusión para una prueba de hipótesis es que o bien tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad, o no tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad.

    Intervalo de confianza para la diferencia entre la proporción de dos poblaciones (Intervalo 2-Prop)

    El intervalo de confianza para la diferencia en proporciones tiene las mismas variables y proporciones aleatorias y los mismos supuestos que la prueba de hipótesis para dos proporciones. Si ya has completado la prueba de hipótesis, entonces no necesitas declararlas nuevamente. Si no ha completado la prueba de hipótesis, entonces indique las variables y proporciones aleatorias y el estado y verifique los supuestos antes de completar el paso del intervalo de confianza

    1. Encuentre los estadísticos de la muestra y el intervalo de confianza Proporción de la
      muestra:
      \(\begin{array}{ll}{n_{1}=\text { size of sample } 1} & {n_{2}=\text { size of sample } 2} \\ {\hat{p}_{1}=\dfrac{x_{1}}{n_{1}}(\text { sample } 1 \text { proportion) }} & {\hat{p}_{2}=\dfrac{x_{2}}{n_{2}} \text { (sample } 2 \text { proportion) }} \\ {\hat{q}_{1}=1-\hat{p}_{1}\left(\text { complement of } \hat{p}_{1}\right)} & {\hat{q}_{2}=1-\hat{p}_{2} \text { (complement of } \hat{p}_{2} )}\end{array}\)
      Intervalo de confianza:
      La estimación del intervalo de confianza de la diferencia\(p_{1}-p_{2}\) es
      \(\left(\hat{p}_{1}-\hat{p}_{2}\right)-E<p_{1}-p_{2}<\left(\hat{p}_{1}-\hat{p}_{2}\right)+E\)
      donde margen de error E viene dado por\( E=z_{c} \sqrt{\dfrac{\hat{p}_{1} \hat{q}_{1}}{n_{1}}+\dfrac{\hat{p}_{2} \hat{q}_{2}}{n_{2}}}\)
      \(z_{c}\) = valor crítico
    2. Interpretación estadística: En general esto parece, “hay una probabilidad de C% que\(\left(\hat{p}_{1}-\hat{p}_{2}\right)-E<p_{1}-p_{2}<\left(\hat{p}_{1}-\hat{p}_{2}\right)+E\) contiene la verdadera diferencia de proporciones”.
    3. Interpretación del Mundo Real: Aquí es donde declaras cuánto más (o menos) es la primera proporción de la segunda proporción.

    El valor crítico es un valor de la distribución normal. Dado que se encuentra un intervalo de confianza sumando y restando un margen de cantidad de error de la proporción de muestra, y el intervalo tiene una probabilidad de ser verdadero, entonces se puede pensar en esto como la afirmación\(P\left(\left(\hat{p}_{1}-\hat{p}_{2}\right)-E<p_{1}-p_{2}<\left(\hat{p}_{1}-\hat{p}_{2}\right)+E\right)=C\). Entonces puedes usar el comando InvNorm en la calculadora TI-83/84 o qnorm en R para encontrar el valor crítico. Estos son siempre el mismo valor, por lo que es más fácil simplemente mirar la tabla A.1 en el Apéndice.

    Ejemplo\(\PageIndex{1}\) hypothesis test for two population proportions

    ¿Los maridos engañan a sus esposas más de lo que las esposas engañan a sus maridos (“Statistics brain”, 2013)? Supongamos que tomas un grupo de 1000 maridos seleccionados al azar y descubres que 231 habían engañado a sus esposas. Supongamos que en un grupo de 1200 esposas seleccionadas al azar, 176 engañaron a sus maridos. ¿Los datos muestran que la proporción de esposos que engañan a sus esposas es mayor que la proporción de esposas que engañan a sus esposos? Prueba al nivel del 5%.

    1. Indicar las variables aleatorias y los parámetros en palabras.
    2. Indicar las hipótesis nulas y alternativas y el nivel de significación.
    3. Indicar y verificar los supuestos para una prueba de hipótesis.
    4. Encuentre los estadísticos de muestra, el estadístico de prueba y el valor p.
    5. Conclusión
    6. Interpretación

    Solución

    1. \(x_{1}\)= número de maridos que engañan a su esposa

    \(x_{2}\)= número de esposas que engañan a su marido

    \(p_{1}\)= proporción de maridos que engañan a su esposa

    \(p_{2}\)= proporción de esposas que engañan a su marido

    2. \(\begin{array}{ll}{H_{o} : p_{1}=p_{2}} & {\text { or } \quad H_{o} : p_{1}-p_{2}=0} \\ {H_{A} : p_{1}>p_{2}} &\quad\quad\: {H_{A} : p_{1}-p_{2}>0} \\ {a=0.05}\end{array}\)

    3.

    1. Se toma una simple muestra aleatoria de 1000 respuestas sobre trampas de maridos. Esto se planteó en el problema. Se toma una simple muestra aleatoria de 1200 respuestas sobre el engaño de las esposas. Esto se planteó en el problema.
    2. Las muestras son independientes. Esto es cierto ya que las muestras involucraron diferentes géneros.
    3. Las propiedades de la distribución binomial se satisfacen en ambas poblaciones. Esto es cierto ya que solo hay dos respuestas, hay un número fijo de ensayos, la probabilidad de éxito es la misma, y los ensayos son independientes.
    4. Las distribuciones de muestreo de\(\hat{p}_{1}\) y\(\hat{p}_{2}\) pueden aproximarse con una distribución normal.
      \(x_{1}=231, n_{1}-x_{1}=1000-231=769, x_{2}=176\), y todos
      \(n_{2}-x_{2}=1200-176=1024\) son mayores o iguales a 5. Así que ambas distribuciones de muestreo de\(\hat{p}_{1}\) y\(\hat{p}_{2}\) pueden aproximarse con una distribución normal.

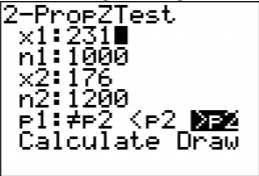
    4. Proporción de muestra:

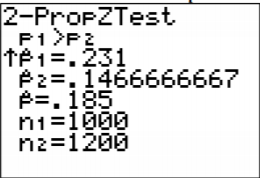
    \(\begin{array}{ll}{n_{1}=1000} & {n_{2}=1200} \\ {\hat{p}_{1}=\dfrac{231}{1000}=0.231} & {\hat{p}_{2}=\dfrac{176}{1200} \approx 0.1467} \\ {\hat{q}_{1}=1-\dfrac{231}{1000}=\dfrac{769}{1000}=0.769} & {\hat{q}_{2}=1-\dfrac{176}{1200}=\dfrac{1024}{1200} \approx 0.8533}\end{array}\)

    Proporción de muestra agrupada,\(\overline{p}\):

    \(\begin{array}{l}{\overline{p}=\dfrac{231+176}{1000+1200}=\dfrac{407}{2200}=0.185} \\ {\overline{q}=1-\dfrac{407}{2200}=\dfrac{1793}{2200}=0.815}\end{array}\)

    Estadística de prueba:

    \(z=\dfrac{(0.231-0.1467)-0}{\sqrt{\dfrac{0.185 * 0.815}{1000}+\dfrac{0.185 * 0.815}{1200}}}\)

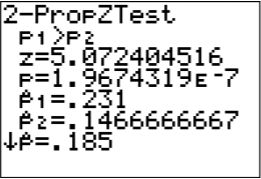
    \(=5.0704\)

    valor p:

    En TI-83/84: normalcdf\((5.0704,1 E 99,0,1)=1.988 \times 10^{-7}\)

    En R:\(1-\text { pnorm }(5.0704,0,1)=1.988 \times 10^{-7}\)

    Captura de pantalla (158) .png
    Figura\(\PageIndex{1}\): Configuración para 2-PROPZTest en la calculadora TI-83/84
    Captura de pantalla (159) .png
    Figura\(\PageIndex{2}\): Resultados para 2-PROPZTest en la calculadora TI-83/84
    Captura de pantalla (160) .png
    Figura\(\PageIndex{3}\): Resultados para 2-PROPZTest en TI-83/84: Calculadora

    En R: prop.test\(\left(c\left(x_{1}, x_{2}\right), c\left(n_{1}, n_{2}\right), \text { alternative }=\right.\) “menos” o “mayor”. Para este ejemplo, prop.test (c (231,176), c (1000, 1200), alternative="mayor”)

    Prueba de 2 muestras para igualdad de proporciones con corrección de continuidad

    datos: c (231, 176) de c (1000, 1200)

    X-cuadrado = 25.173, df = 1, valor p = 2.621e-07

    hipótesis alternativa: mayor

    Intervalo de confianza del 95 por ciento:

    0.05579805 1.00000000

    estimaciones de la muestra:

    prop 1 prop 2

    0.2310000 0.1466667

    Nota

    La respuesta de R es el valor p. Es diferente de la fórmula o la calculadora TI-83/84 debido a una corrección de continuidad que hace R.

    5. Conclusión

    Rechazar\(H_{o}\), ya que el valor p es menor al 5%.

    6. Interpretación Esta es evidencia suficiente para demostrar que la proporción de esposos que tienen asuntos es mayor que la proporción de esposas que tienen asuntos.

    Ejemplo\(\PageIndex{2}\) confidence interval for two population properties

    ¿Más maridos engañan más a sus esposas que las esposas engañan a los esposos (“Statistics brain”, 2013)? Supongamos que tomas un grupo de 1000 maridos seleccionados al azar y descubres que 231 habían engañado a sus esposas. Supongamos que en un grupo de 1200 esposas seleccionadas al azar, 176 engañaron a sus maridos. Estimar la diferencia en la proporción de esposos y esposas que engañan a sus cónyuges utilizando un nivel de confianza del 95%.

    1. Indicar las variables aleatorias y los parámetros en palabras.
    2. Indicar y verificar los supuestos para el intervalo de confianza.
    3. Encuentra las estadísticas de la muestra y el intervalo de confianza.
    4. Interpretación Estadística
    5. Interpretación del mundo real

    Solución

    1. Estos fueron declarados en Ejemplo\(\PageIndex{1}\), pero se reproducen aquí como referencia.

    \(x_{1}\)= número de maridos que engañan a su esposa

    \(x_{2}\)= número de esposas que engañan a su marido

    \(p_{1}\)= proporción de maridos que engañan a su esposa

    \(p_{2}\)= proporción de esposas que engañan a su marido

    2. Los supuestos fueron declarados y comprobados en Ejemplo\(\PageIndex{1}\).

    3. Proporción de muestra:

    \(\begin{array}{ll}{n_{1}=1000} & {n_{2}=1200} \\ {\hat{p}_{1}=\dfrac{231}{1000}=0.231} & {\hat{p}_{2}=\dfrac{176}{1200} \approx 0.1467} \\ {\hat{q}_{1}=1-\dfrac{231}{1000}=\dfrac{769}{1000}=0.769} & {\hat{q}_{2}=1-\dfrac{176}{1200}=\dfrac{1024}{1200} \approx 0.8533}\end{array}\)

    Intervalo de confianza:

    \(\begin{array}{l}{z_{c}=1.96} \\ {E=1.96 \sqrt{\dfrac{0.231 * 0.769}{1000}+\dfrac{0.1467 * 0.8533}{1200}}=0.033}\end{array}\)

    La estimación del intervalo de confianza de la diferencia\(p_{1}-p_{2}\) es

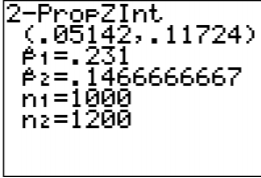
    \(\begin{array}{l}{\left(\hat{p}_{1}-\hat{p}_{2}\right)-E<p_{1}-p_{2}<\left(\hat{p}_{1}-\hat{p}_{2}\right)+E} \\ {(0.231-0.1467)-0.033<p_{1}-p_{2}<(0.231-0.1467)+0.033} \\ {0.0513<p_{1}-p_{2}<0.1173}\end{array}\)

    Captura de pantalla (161) .png
    Figura 9.1.4: Configuración para 2-PROPZint en la calculadora TI-83/84
    Captura de pantalla (162) .png
    Figura\(\PageIndex{5}\): Resultados para 2-PROPzint en la calculadora TI-83/84

    En R: prop.test\(\left(c\left(x_{1}, x_{2}\right), c\left(n_{1}, n_{2}\right), \text { conf.level }=\mathrm{C}\right)\), donde C está en forma decimal. Para este ejemplo, prop.test (c (231,176), c (1000, 1200), conf.level=0.95)

    Prueba de 2 muestras para igualdad de proporciones con corrección de continuidad

    datos: c (231, 176) de c (1000, 1200)

    X-cuadrado = 25.173, df = 1, valor p = 5.241e-07

    hipótesis alternativa: dos.sided

    Intervalo de confianza del 95 por ciento:

    0.05050705 0.11815962

    estimaciones de la muestra:

    prop 1 prop 2

    0.2310000 0.1466667

    Nota

    La respuesta de R es el intervalo de confianza. Es diferente de la fórmula o la calculadora TI-83/84 debido a una corrección de continuidad que hace R.

    4. Interpretación estadística: Existe un 95% de probabilidad que\(0.0505<p_{1}-p_{2}<0.1182\) contenga la verdadera diferencia de proporciones.

    5. Interpretación del Mundo Real: La proporción de maridos que engañan es entre 5.05% y 11.82% mayor que la proporción de esposas que engañan.

    Testo

    Ejercicio\(\PageIndex{1}\)

    En cada problema se muestran todos los pasos de la prueba de hipótesis o intervalo de confianza. Si no se cumplen algunos de los supuestos, tenga en cuenta que los resultados de la prueba o intervalo pueden no ser correctos y luego continuar el proceso de la prueba de hipótesis o intervalo de confianza.

    1. Muchos estudiantes de secundaria toman las pruebas AP en diferentes áreas temáticas. En 2007, de los 144 mil 796 alumnos que tomaron el examen de biología 84 mil 199 de ellos eran mujeres. En ese mismo año, de los 211 mil 693 alumnos que tomaron el examen AB de cálculo 102 mil 598 de ellos eran mujeres (“Puntuaciones del examen AP”, 2013). ¿Hay evidencia suficiente para demostrar que la proporción de alumnas que toman el examen de biología es mayor que la proporción de alumnas que toman el examen AB de cálculo? Prueba al nivel del 5%.
    2. Muchos estudiantes de secundaria toman las pruebas AP en diferentes áreas temáticas. En 2007, de los 144 mil 796 alumnos que tomaron el examen de biología 84 mil 199 de ellos eran mujeres. En ese mismo año, de los 211 mil 693 alumnos que tomaron el examen AB de cálculo 102 mil 598 de ellos eran mujeres (“Puntuaciones del examen AP”, 2013). Estimar la diferencia en la proporción de alumnas que toman el examen de biología y alumnas que toman el examen AB de cálculo utilizando un nivel de confianza del 90%.
    3. Muchos estudiantes de secundaria toman las pruebas AP en diferentes áreas temáticas. En 2007, de los 211 mil 693 alumnos que tomaron el examen AB de cálculo 102 mil 598 de ellos eran mujeres y 109 095 de ellos eran varones (“Puntuaciones del examen AP”, 2013). ¿Hay evidencia suficiente para demostrar que la proporción de alumnas que toman el examen AB de cálculo es diferente de la proporción de estudiantes varones que toman el examen AB de cálculo? Prueba al nivel del 5%.
    4. Muchos estudiantes de secundaria toman las pruebas AP en diferentes áreas temáticas. En 2007, de los 211 mil 693 alumnos que tomaron el examen AB de cálculo 102 mil 598 de ellos eran mujeres y 109 095 de ellos eran varones (“Puntuaciones del examen AP”, 2013). Estimar usando un nivel de 90% la diferencia en la proporción de alumnas que toman el examen AB de cálculo versus estudiantes varones que toman el examen AB de cálculo.
    5. ¿Hay más niños diagnosticados con Trastorno del Espectro Autista (TEA) en estados que tienen áreas urbanas más grandes sobre estados que en su mayoría son rurales? En el estado de Pensilvania, un estado bastante urbano, hay 245 niños de ocho años diagnosticados con TEA de 18,440 niños de ocho años evaluados. En el estado de Utah, un estado bastante rural, hay 45 niños de ocho años diagnosticados con TEA de los 2,123 niños de ocho años evaluados (“Autismo y desarrollo”, 2008). ¿Hay evidencia suficiente para demostrar que la proporción de niños diagnosticados con TEA en Pensilvania es mayor que la proporción en Utah? Prueba al nivel del 1%.
    6. ¿Hay más niños diagnosticados con Trastorno del Espectro Autista (TEA) en estados que tienen áreas urbanas más grandes sobre estados que en su mayoría son rurales? En el estado de Pensilvania, un estado bastante urbano, hay 245 niños de ocho años diagnosticados con TEA de 18,440 niños de ocho años evaluados. En el estado de Utah, un estado bastante rural, hay 45 niños de ocho años diagnosticados con TEA de los 2,123 niños de ocho años evaluados (“Autismo y desarrollo”, 2008). Estimar la diferencia en proporción de niños diagnosticados con TEA entre Pensilvania y Utah. Usa un nivel de confianza del 98%.
    7. Un niño que muere por una intoxicación accidental es un incidente terrible. ¿Es más probable que un niño varón se meta en veneno que una niña? Para averiguarlo, se recolectaron datos que mostraron que de 1830 niños de entre uno y cuatro años que pasan por envenenamiento, 1031 eran varones y 799 mujeres (Flanagan, Rooney & Griffiths, 2005). ¿Los datos muestran que hay más niños varones que mueren por envenenamiento que niñas? Prueba al nivel 1%.
    8. Un niño que muere por una intoxicación accidental es un incidente terrible. ¿Es más probable que un niño varón se meta en veneno que una niña? Para averiguarlo, se recolectaron datos que mostraron que de 1830 niños de entre uno y cuatro años que pasan por envenenamiento, 1031 eran varones y 799 mujeres (Flanagan, Rooney & Griffiths, 2005). Calcular un intervalo de confianza del 99% para la diferencia en proporciones de muertes por envenenamiento de niños y niñas de uno a cuatro años de edad.
    Contestar

    Para todas las pruebas de hipótesis, solo se da la conclusión. Para todos los intervalos de confianza, solo se da el intervalo usando la tecnología (Software R). Ver solución para toda la respuesta.

    1. Rechazar Ho
    2. \(0.0941<p_{1}-p_{2}<0.0996\)
    3. Rechazar Ho
    4. \(-0.0332<p_{1}-p_{2}<-0.0282\)
    5. No rechazar a Ho
    6. \(-0.01547<p_{1}-p_{2}<-0.0001\)
    7. Rechazar Ho
    8. \(0.0840<p_{1}-p_{2}<0.1696\)

    This page titled 9.1: Dos proporciones is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Kathryn Kozak via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.