9.2: Muestras emparejadas para dos medias
- Page ID
- 149705
¿Dos poblaciones son iguales? ¿La estatura promedio de los hombres es más alta que la estatura promedio de las mujeres? ¿El peso medio es menor después de una dieta que antes?
Se pueden comparar poblaciones comparando sus medias. Se toma una muestra de cada población y se comparan las estadísticas.
Cada vez que comparas dos poblaciones necesitas saber si las muestras son independientes o dependientes. Las fórmulas que utilice son diferentes para diferentes tipos de muestras.
Si la forma en que eliges una muestra no tiene ningún efecto en la forma en que eliges la otra, las dos muestras son independientes. La manera de pensarlo es que en muestras independientes, los individuos de una muestra son en general diferentes de los individuos de la otra muestra. Esto significará que la muestra uno no tiene ningún efecto sobre la muestra dos. Los valores de muestra de una muestra no están relacionados o emparejados con valores de la otra muestra.
Si elige las muestras para que una medición en una muestra se empareja con una medición de la otra muestra, las muestras son dependientes o emparejadas o emparejadas. (A menudo una situación de antes y después.) Desea asegurarse de que hay un significado para emparejar valores de datos de una muestra con un valor de datos específico de la otra muestra. Una forma de pensarlo es que en muestras dependientes, los individuos de una muestra son los mismos individuos de la otra muestra, aunque puede haber otras razones para emparejar valores. Esto hace que los valores de muestra de cada muestra se emparejen.
Ejemplo\(\PageIndex{1}\) independent or dependent samples
Determinar si las siguientes son muestras dependientes o independientes.
- Escoge al azar 5 hombres y 6 mujeres y compara sus alturas.
- Elige 10 hombres y pesalos. Dales un nuevo medicamento para la dieta Wonder y luego pesarlos nuevamente.
- Tomar 10 personas y medir la fuerza de su brazo dominante y su brazo no dominante.
Solución
- Independiente, ya que no hay razón para que un valor pertenezca a otro. Los individuos no son los mismos para ambas muestras. Los individuos son definitivamente diferentes. Una manera de pensar sobre esto es que el conocimiento de que un hombre es elegido en una muestra no da ninguna información sobre ninguna de las mujeres elegidas en la otra muestra.
- Dependiente, ya que el peso de antes de cada persona puede ser igualado con su peso posterior. Los individuos son los mismos para ambas muestras. Una forma de pensar sobre esto es que el conocimiento de que una persona pesa 400 libras al principio te dirá algo sobre su peso después del medicamento dietético.
- Dependiente, ya que puedes igualar las fortalezas de los dos brazos. Los individuos son los mismos para ambas muestras. Por lo que el conocimiento de la fuerza dominante del brazo de una persona te dirá algo sobre la fuerza de su brazo no dominante.
Para analizar los datos cuando hay muestras emparejadas o emparejadas, llamadas muestras dependientes, se realiza una prueba t pareada. Dado que las muestras son coincidentes, se puede encontrar la diferencia entre los valores de las dos variables aleatorias.
Prueba de hipótesis para prueba t pareada de dos muestras
- Indicar las variables aleatorias y los parámetros en palabras.
\(x_{1}\)= variable aleatoria 1
\(x_{2}\) = variable aleatoria 2
\(\mu_{1}\) = media de la variable aleatoria 1
\(\mu_{2}\) = media de la variable aleatoria 2 - Declarar las hipótesis nulas y alternativas y el nivel de significación Las hipótesis habituales serían
\(\begin{array}{ll}{H_{o} : \mu_{1}=\mu_{2} \text { or }} & {H_{o} : \mu_{1}-\mu_{2}=0} \\ {H_{A} : \mu_{1}<\mu_{2}} & {H_{A} : \mu_{1}-\mu_{2}<0} \\ {H_{A} : \mu_{1}>\mu_{2}} & {H_{A} : \mu_{1}-\mu_{2}>0} \\ {H_{A} : \mu_{1} \neq \mu_{2}} & {H_{A} : \mu_{1}-\mu_{2} \neq 0}\end{array}\)
Sin embargo, ya que estás encontrando las diferencias, entonces realmente puedes pensar en el valor medio\(\mu_{1}-\mu_{2}=\mu_{\sigma} \mu_{d}=\) poblacional de las diferencias,
Entonces el las hipótesis se convierten
\(\begin{array}{l}{H_{o} : \mu_{d}=0} \\ {H_{1} : \mu_{d}<0} \\ {H_{A} : \mu_{d}>0} \\ {H_{A} : \mu_{d} \neq 0}\end{array}\)
También, indique aquí su\(\alpha\) nivel. - Indicar y verificar los supuestos para la prueba de hipótesis
- Se toma una muestra aleatoria de n pares.
- La población de la diferencia entre variables aleatorias se distribuye normalmente. En este caso la población que te interesa tiene que ver con las diferencias que encuentres. No importa si cada variable aleatoria se distribuye normalmente. Solo es importante si las diferencias que encuentras están normalmente distribuidas. Al igual que antes, la prueba t es bastante robusta a la suposición de que el tamaño de la muestra es grande. Esto significa que si no se cumple esta suposición, pero el tamaño de su muestra es bastante grande (más de 30), entonces los resultados de la prueba t son válidos.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p Estadística de la
muestra:
Diferencia:\(d=x_{1}-x_{2}\) para cada par Media
muestral de las diferencias: Desviación\(\overline{d}=\dfrac{\sum d}{n}\)
estándar de las diferencias:\(s_{d}=\dfrac{\sum(d-\overline{d})^{2}}{n-1}\)
Número de pares: n Estadístico de
prueba:
\(t=\dfrac{\overline{d}-\mu_{d}}{\dfrac{s_{d}}{\sqrt{n}}}\)
con grados de libertad = df = n - 1valor p:Nota
\(\mu_{d}=0\)en la mayoría de los casos.
En TI-83/84: Usar tcdf (límite inferior, límite superior, df)En R: Usar pt (t, df)Nota
Si\(H_{A} : \mu_{d}<0\), entonces el límite inferior es\(-1 E 99\) y el límite superior es su estadística de prueba. Si\(H_{A} : \mu_{d}>0\), entonces el límite inferior es su estadística de prueba y el límite superior es\(1 E 99\). Si\(H_{A} : \mu_{d} \neq 0\), entonces encuentre el valor p para\(H_{A} : \mu_{d}<0\), y multiplique por 2.)
Nota
Si\(H_{A} : \mu_{d}<0\), use pt (t, df). Si\(H_{A} : \mu_{d}>0\), use 1 - pt (t, df). Si\(H_{A} : \mu_{d} \neq 0\), entonces encuentra el valor p para\(H_{A} : \mu_{d}<0\), y multiplica por 2
- Aquí es donde escribes rechazar\(H_{o}\) o no rechazas\(H_{o}\). La regla es: si el valor p <\(\alpha\), entonces rechazar\(H_{o}\). Si el valor p\(\geq \alpha\), entonces no puede rechazar\(H_{o}\).
- Aquí es donde interpretas en términos del mundo real la conclusión a la prueba. La conclusión para una prueba de hipótesis es que o bien tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad, o no tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad.
Intervalo de confianza para la diferencia en medias de muestras pareadas (intervalo T)
El intervalo de confianza para la diferencia en medias tiene las mismas variables y medias aleatorias y los mismos supuestos que la prueba de hipótesis para dos muestras pareadas. Si ya has completado la prueba de hipótesis, entonces no necesitas declararlas nuevamente. Si no ha completado la prueba de hipótesis, entonces indique las variables y medias aleatorias, y establezca y verifique las suposiciones antes de completar el paso del intervalo de confianza.
- Encuentra el estadístico muestral y el intervalo de confianza Estadística de
muestra:
Diferencia: d = Media\(x_{1}-x_{2}\)
muestral de las diferencias: Desviación\(\overline{d}=\dfrac{\sum{d}}{n}\)
estándar de las diferencias:\(s_{d}=\dfrac{\sum(d-\overline{d})^{2}}{n-1}\)
Número de pares: n
Intervalo de confianza:
La estimación del intervalo de confianza de la diferencia\(\mu_{d}=\mu_{1}-\mu_{2}\)
\(\begin{array}{l}{\overline{d}-E<\mu_{d}<\overline{d}+E} \\ {E=t_{c} \dfrac{s_{d}}{\sqrt{n}}}\end{array}\)
\(t_{c}\) es el valor crítico donde grados de libertad df = n - 1 - Interpretación estadística: En general esto parece, “existe una probabilidad de C% de que la afirmación\(\overline{d}-E<\mu_{d}<\overline{d}+E\) contenga la verdadera diferencia de medias”.
- Interpretación del Mundo Real: Aquí es donde declaras qué intervalo contiene la verdadera diferencia de medias.
El valor crítico es un valor de la distribución t de Student. Dado que se encuentra un intervalo de confianza sumando y restando un margen de cantidad de error de la media de la muestra, y el intervalo tiene una probabilidad de contener la verdadera diferencia de medias, entonces puede pensar en esto como la declaración\(P\left(\overline{d}-E<\mu_{d}<\overline{d}+E\right)=C\). Para encontrar el valor crítico, usa la tabla A.2 en el Apéndice.
Cómo verificar los supuestos de prueba t e intervalo de confianza:
Para que la prueba t o el intervalo de confianza sean válidos, se deben cumplir los supuestos de la prueba. Entonces, siempre que ejecutes una prueba t o un intervalo de confianza, debes asegurarte de que se cumplan las suposiciones. Por lo que hay que revisarlos. Así es como haces esto:
- Para el supuesto de que la muestra es una muestra aleatoria, describa cómo tomó las muestras. Asegúrese de que su técnica de muestreo sea aleatoria y que las muestras fueran dependientes.
- Para el supuesto de que la población de las diferencias es normal, recuerde el proceso de evaluación de la normalidad a partir del capítulo 6.
Ejemplo\(\PageIndex{2}\) hypothesis test for paired samples using the formula
Un investigador quiere ver si un programa de pérdida de peso es efectivo. Mide el peso de 6 mujeres seleccionadas al azar antes y después del programa de pérdida de peso (ver Ejemplo\(\PageIndex{1}\)). ¿Hay evidencia de que el programa de pérdida de peso es efectivo? Prueba al nivel del 5%.
| Persona | 1 | 2 | 3 | 4 | 5 | 6 |
| Peso antes | 165 | 172 | 181 | 185 | 168 | 175 |
| Peso después | 143 | 151 | 156 | 161 | 152 | 154 |
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar las hipótesis nulas y alternativas y el nivel de significación.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
- Conclusión
- Interpretación
Solución
1. \(x_{1}\)= peso de una mujer después del programa de pérdida de peso
\(x_{2}\)= peso de una mujer antes del programa de pérdida de peso
\(\mu_{1}\)= peso medio de una mujer después del programa de pérdida de peso
\(\mu_{2}\)= peso promedio de una mujer antes del programa de pérdida de peso
2. \(\begin{array}{l}{H_{o} : \mu_{d}=0} \\ {H_{A} : \mu_{d}<0} \\ {\alpha=0.05}\end{array}\)
3.
- Se tomó una muestra aleatoria de 6 pares de pesos antes y después. Esto se afirmó en el problema, ya que las mujeres fueron elegidas al azar.
- La población de la diferencia en los pesos después y antes se distribuye normalmente. Para ver si esto es cierto, mire el histograma, el número de valores atípicos y la gráfica de probabilidad normal. (Si lo desea, puede mirar primero la gráfica de probabilidad normal. Si no se ve lineal, entonces es posible que desee mirar el histograma y el número de valores atípicos en este punto).
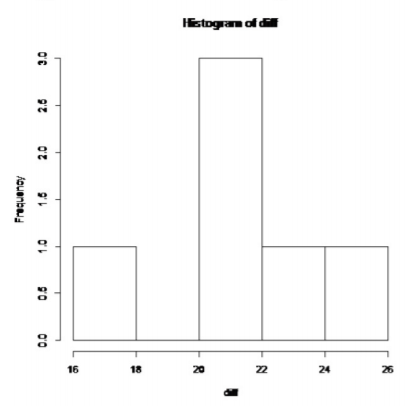.png)
Este histograma se ve algo en forma de campana.
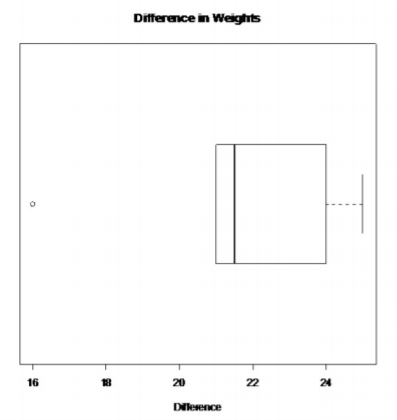.png)
Solo hay un valor atípico en el conjunto de datos de diferencia.
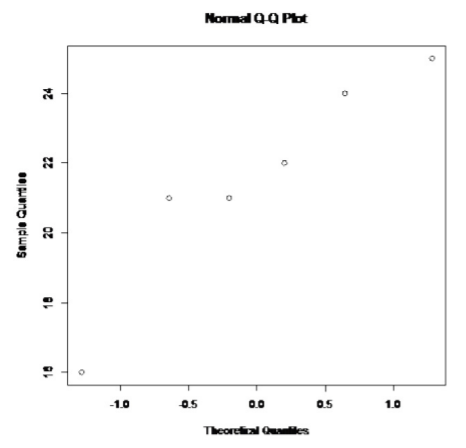.png)
La gráfica de probabilidad sobre las diferencias parece algo lineal. Por lo que se puede suponer que la distribución de la diferencia de pesos es normal.
4. Estadísticas de muestra:
| Persona | 1 | 2 | 3 | 4 | 5 | 6 |
| Peso después,\(x_{1}\) | 143 | 151 | 156 | 161 | 152 | 154 |
| Peso antes,\(x_{2}\) | 165 | 172 | 181 | 185 | 168 | 175 |
| d =\(x_{1}-x_{2}\) | -22 | -21 | -25 | -24 | -16 | -21 |
La media y la desviación estándar son
\(\begin{array}{l}{\overline{d}=-21.5} \\ {s_{d}=3.15}\end{array}\)
Estadística de prueba:
\(t=\dfrac{\overline{d}-\mu_{d}}{s_{d} / \sqrt{n}}=\dfrac{-21.5-0}{3.15 / \sqrt{6}}=-16.779\)
valor p:
Hay seis pares así que los grados de libertad son
df = n - 1 = 6 - 1 = 5
Desde\(H_{1} : \mu_{d}<0\), entonces el valor p
Usando TI-83/84: tcdf\((-1 E 99,-16.779,5) \approx 6.87 \times 10^{-6}\)
Usando R: pt\((-16.779,5) \approx 6.87 \times 10^{-6}\)
5. Desde el valor p < 0.05, rechazar\(H_{o}\).
6. Hay evidencia suficiente para demostrar que el programa de pérdida de peso es efectivo.
Nota
El hecho de que la prueba de hipótesis diga que el programa es efectivo no significa que debas salir y usarlo de inmediato. El programa tiene significancia estadística, pero eso no significa que tenga significación práctica. Necesitas ver cuánto peso pierde una persona, y debes mirar qué tan segura es, qué tan costosa, funciona a largo plazo y otras preguntas de tipo. Recuerda mirar el significado práctico en todas las situaciones. En este caso, la pérdida de peso promedio fue de 21.5 libras, lo que es muy prácticamente significativo. Recuerda mirar también la seguridad y el gasto del medicamento.
Ejemplo\(\PageIndex{3}\) hypothesis Test for Paired Samples Using Technology
La Fuerza Aérea de Nueva Zelanda compró un lote de cascos de vuelo. Después se enteraron de que los cascos no encajaban. Para asegurarse de que ordenan el tamaño correcto de los cascos, midieron el tamaño de cabeza de los reclutas. Para ahorrar dinero, querían usar pinzas de cartón, pero no estaban seguros de si serían lo suficientemente precisas. Por lo que tomaron 18 reclutas y midieron sus cabezas con las pinzas de cartón y también con pinzas metálicas. Los datos en centímetros (cm) están en Ejemplo\(\PageIndex{3}\) (“Talla casco NZ”, 2013). ¿Los datos proporcionan evidencia suficiente para demostrar que existe una diferencia en las mediciones entre las pinzas de cartón y metal? Utilizar un nivel de significancia del 5%.
| Cartón | Metal |
|---|---|
| 146 | 145 |
| 151 | 153 |
| 163 | 161 |
| 152 | 151 |
| 151 | 145 |
| 151 | 150 |
| 149 | 150 |
| 166 | 163 |
| 149 | 147 |
| 155 | 154 |
| 155 | 150 |
| 156 | 156 |
| 162 | 161 |
| 150 | 152 |
| 156 | 154 |
| 158 | 154 |
| 149 | 147 |
| 163 | 160 |
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar las hipótesis nulas y alternativas y el nivel de significación.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
- Conclusión
- Interpretación
Solución
1. \(x_{1}\)= medición de la cabeza del recluta usando un calibrador de cartón
\(x_{2}\)= medición de la cabeza de recluta usando pinza metálica
\(\mu_{1}\)= medición media de la cabeza del recluta usando un calibrador de cartón
\(\mu_{2}\)= medición media de la cabeza del recluta usando un calibrador de metal
2. \(\begin{array}{l}{H_{o} : \mu_{d}=0} \\ {H_{A} : \mu_{d} \neq 0} \\ {\alpha=0.05}\end{array}\)
3.
- Se tomó una muestra aleatoria de 18 pares de medidas de cabeza de reclutas con cartón y calibre metálico. Esto no fue declarado, pero probablemente podría asumirse con seguridad.
- La población de la diferencia en las medidas de cabeza entre las pinzas de cartón y metal se distribuye normalmente. Para ver si esto es cierto, mire el histograma, el número de valores atípicos y la gráfica de probabilidad normal. (Si lo desea, puede mirar primero la gráfica de probabilidad normal. Si no se ve lineal, entonces es posible que desee mirar el histograma y el número de valores atípicos en este punto).
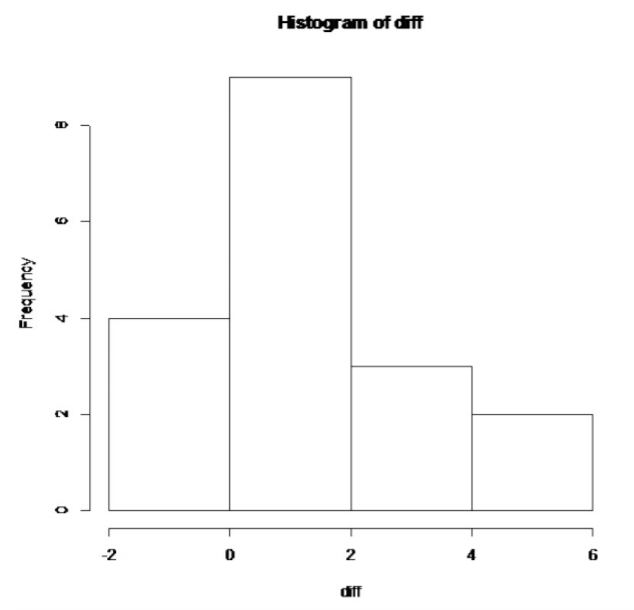.png)
Este histograma se ve en forma de campana.
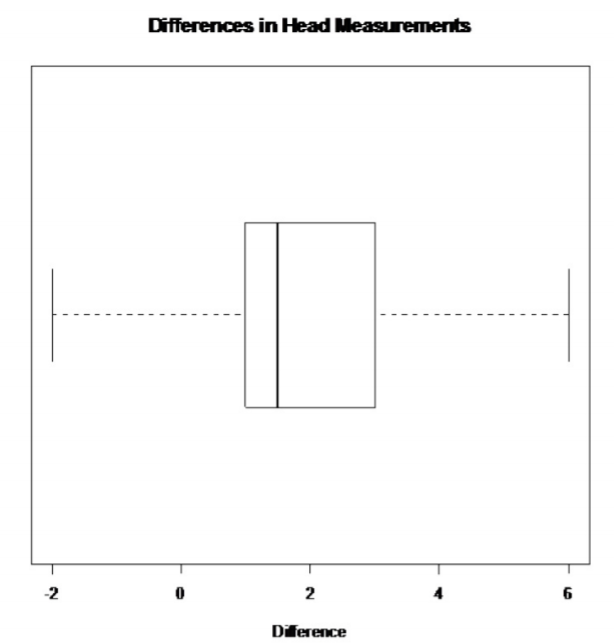.png)
No hay valores atípicos en el conjunto de datos de diferencia.
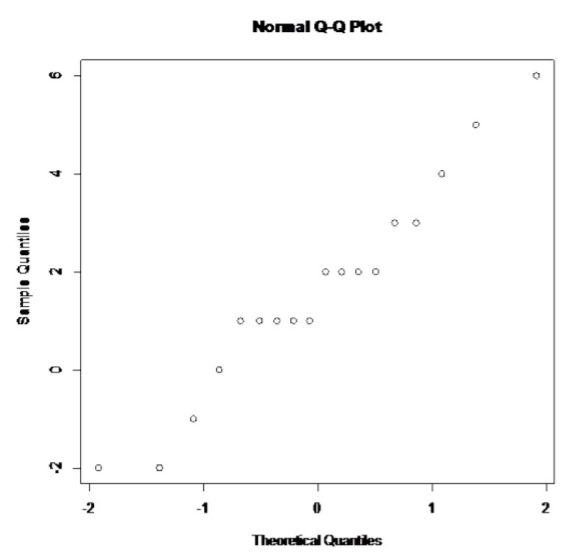.png)
La gráfica de probabilidad sobre las diferencias parece algo lineal.
Por lo que se puede suponer que la distribución de la diferencia de pesos es normal.
4. Usando el TI-83/84, poner\(x_{1}\) en L1 y\(x_{2}\) en L2. Después vaya al nombre L3, y escriba L 1- L 2. La calculadora calculará las diferencias por ti y las pondrá en L3. Ahora entra en STAT y pasa a PRUEBAS. Elija T-Test. La configuración de la calculadora está en la Figura\(\PageIndex{7}\).
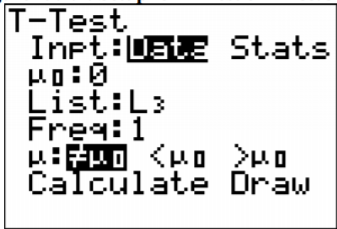.png)
Una vez que presione ENTRAR en Calcular verá el resultado que se muestra en la Figura\(\PageIndex{8}\).
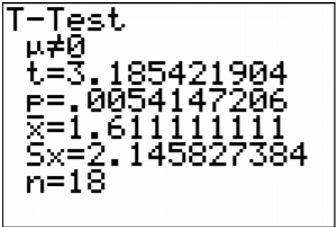.png)
Usando R: comando es t.test (variable1, variable2, pareado = VERDADERO, alternativa = “menos” o “mayor”). Para este ejemplo, el comando sería t.test (cartón, metal, pareado = VERDADERO)
Prueba t pareada
datos: cartón y metal
t = 3.1854, df = 17, valor p = 0.005415
hipótesis alternativa: la verdadera diferencia en medias no es igual a 0
Intervalo de confianza del 95 por ciento:
0.5440163 2.6782060
estimaciones de muestra:
media de las diferencias
1.611111
El t = 3.185 es el estadístico de prueba. El valor p es 0.0054147206.
5. Desde el valor p < 0.05, rechazar\(H_{o}\).
6. Hay suficiente evidencia para mostrar que las medidas medias de la cabeza usando las pinzas de cartón no son las mismas que cuando se usan las pinzas metálicas. Entonces parece que la Fuerza Aérea de Nueva Zelanda no debería usar las pinzas de cartón.
Ejemplo\(\PageIndex{4}\) confidence interval for paired samples using the formula
Un investigador quiere estimar la pérdida media de peso que experimentan las personas usando un nuevo programa. Mide el peso de 6 mujeres seleccionadas al azar antes y después del programa de pérdida de peso (ver Ejemplo\(\PageIndex{1}\)). Encuentra un intervalo de confianza del 90% para la media de la pérdida de peso usando el nuevo programa.
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar y verificar los supuestos para el intervalo de confianza.
- Encuentra el estadístico muestral y el intervalo de confianza.
- Interpretación Estadística
- Interpretación del mundo real
Solución
1. Estos fueron declarados en Ejemplo\(\PageIndex{2}\), pero se reproducen aquí como referencia.
\(x_{1}\)= peso de una mujer después del programa de pérdida de peso
\(x_{2}\)= peso de una mujer antes del programa de pérdida de peso
\(\mu_{1}\)= peso medio de una mujer después del programa de pérdida de peso
\(\mu_{2}\)= peso promedio de una mujer antes del programa de pérdida de peso
2. Los supuestos fueron declarados y comprobados en Ejemplo\(\PageIndex{2}\).
3. Estadísticas de muestra:
De Ejemplo\(\PageIndex{2}\)
\(\begin{array}{l}{\overline{d}=-21.5} \\ {s_{d}=3.15}\end{array}\)
El nivel de confianza es del 90%, por lo que
C= 90%
Hay seis pares, por lo que los grados de libertad son
df = n - 1 = 6 - 1 = 5
Ahora mira en la tabla A.2. Bajar la primera columna a 5, luego pasar a la columna encabezada con 90%.
\(t_{c}=2.015\)
\(E=t_{c} \dfrac{s_{d}}{\sqrt{n}}=2.015 \dfrac{3.15}{\sqrt{6}} \approx 2.6\)
\(\overline{d}-E<\mu_{d}<\overline{d}+E\)
\(-21.5-2.6<\mu_{d}<-21.5+2.6\)
\(-24.1 \text { pounds }<\mu_{d}<-18.9 \text { pounds }\)
4. Existe un 90% de probabilidad que\(-24.1 \text { pounds }<\mu_{d}<-18.9 \text { pounds }\) contenga la verdadera diferencia media en la pérdida de peso.
5. La pérdida media de peso está entre 18.9 y 24.1 libras.
Nota
Los signos negativos te dicen que la primera media es menor que la segunda media, y así una pérdida de peso en este caso.
Ejemplo\(\PageIndex{5}\) confidence interval for paired samples using technology
La Fuerza Aérea de Nueva Zelanda compró un lote de cascos de vuelo. Después se enteraron de que los cascos no encajaban. Para asegurarse de que ordenan el tamaño correcto de los cascos, midieron el tamaño de cabeza de los reclutas. Para ahorrar dinero, querían usar pinzas de cartón, pero no estaban seguros de si serían lo suficientemente precisas. Por lo que tomaron 18 reclutas y midieron sus cabezas con las pinzas de cartón y también con pinzas metálicas. Los datos en centímetros (cm) están en Ejemplo\(\PageIndex{3}\) (“Talla casco NZ”, 2013). Estimar la diferencia media en las mediciones entre las pinzas de cartón y metal utilizando un intervalo de confianza del 95%.
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentra el estadístico muestral y el intervalo de confianza.
- Interpretación Estadística
- Interpretación del mundo real
Solución
1. Estos fueron declarados en Ejemplo\(\PageIndex{3}\), pero se reproducen aquí como referencia.
\(x_{1}\)= medición de la cabeza del recluta usando un calibrador de cartón
\(x_{2}\)= medición de la cabeza de recluta usando pinza metálica
\(\mu_{1}\)= medición media de la cabeza del recluta usando un calibrador de cartón
\(\mu_{2}\)= medición media de la cabeza del recluta usando un calibrador de metal
2. Los supuestos fueron declarados y comprobados en Ejemplo\(\PageIndex{3}\).
3. Usando el TI-83/84, poner\(x_{1}\) en L1 y\(x_{2}\) en L2. Después vaya al nombre L3, y escriba L 1 - L 2. Ahora la calculadora calculará las diferencias por ti y las pondrá en L3. Ahora entra en STAT y pasa a PRUEBAS. Después escogió tInterval. La configuración de la calculadora está en la Figura\(\PageIndex{9}\).
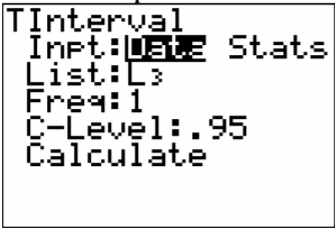.png)
Una vez que presione ENTRAR en Calcular verá el resultado que se muestra en la Figura\(\PageIndex{10}\).
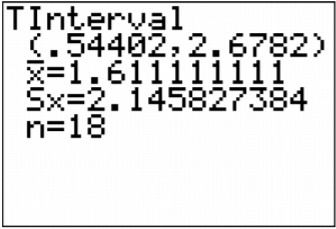.png)
Usando R: el comando es t.test (variable1, variable2, pareado = VERDADERO, conf.level = C), donde C está en forma decimal. Para este ejemplo el comando sería
t.test (cartón, metal, pareado = VERDADERO, conf.nivel=0.95)
Prueba t pareada
datos: cartón y metal
t = 3.1854, df = 17, valor p = 0.005415
hipótesis alternativa: la verdadera diferencia en medias no es igual a 0
Intervalo de confianza del 95 por ciento:
0.5440163 2.6782060
estimaciones de muestra:
media de las diferencias
1.611111
Entonces
\(0.54 \mathrm{cm}<\mu_{d}<2.68 \mathrm{cm}\)
4. Existe un 95% de probabilidad de que\(0.54 \mathrm{cm}<\mu_{d}<2.68 \mathrm{cm}\) contenga la verdadera diferencia media en las medidas de la cabeza entre los calibres de cartón y metal.
5. La diferencia media en las medidas de cabeza entre los calibres de cartón y metal está entre 0.54 y 2.68 cm. Esto significa que los calibres de cartón miden en promedio la cabeza de un recluta para estar entre 0.54 y 2.68 cm más de diámetro que los calibres metálicos. Eso hace parecer que los calibres de cartón no están midiendo lo mismo que los calibres metálicos. (Los valores positivos en el intervalo de confianza implican que la primera media es mayor que la segunda media.)
Los ejemplos 9.2.2 y 9.2.4 utilizan el mismo conjunto de datos, pero uno está realizando una prueba de hipótesis y el otro está realizando un intervalo de confianza. Observe que la conclusión de la prueba de hipótesis fue rechazar\(H_{o}\) y decir que hubo una diferencia en las medias, y el intervalo de confianza no contiene el número 0. Si el intervalo de confianza sí contenía el número 0, entonces eso significaría que las dos medias podrían ser las mismas. Dado que el intervalo no contenía 0, entonces se podría decir que las medias son diferentes al igual que en la prueba de hipótesis. Esto significa que la prueba de hipótesis y el intervalo de confianza pueden producir la misma interpretación. Sin embargo, tenga cuidado, puede ejecutar una prueba de hipótesis con un nivel de significancia particular y un intervalo de confianza con un nivel de confianza que no sea compatible con su nivel de significancia. Esto significará que la conclusión del intervalo de confianza no sería la misma que con una prueba de hipótesis. Entonces, si quieres estimar la diferencia media, entonces realiza un intervalo de confianza. Si quieres demostrar que los medios son diferentes, entonces realiza una prueba de hipótesis.
Testo
Ejercicio\(\PageIndex{1}\)
En cada problema se muestran todos los pasos de la prueba de hipótesis o intervalo de confianza. Si no se cumplen algunos de los supuestos, tenga en cuenta que los resultados de la prueba o intervalo pueden no ser correctos y luego continuar el proceso de la prueba de hipótesis o intervalo de confianza.
- El nivel de colesterol de los pacientes que presentaron ataques cardíacos se midió dos días después del ataque cardíaco y luego nuevamente cuatro días después del ataque cardíaco. Los investigadores quieren ver si el nivel de colesterol de los pacientes que tienen ataques cardíacos disminuye a medida que aumenta el tiempo transcurrido desde su ataque cardíaco. Los datos están en Ejemplo\(\PageIndex{4}\) (“Niveles de colesterol después”, 2013). ¿Los datos muestran que el nivel medio de colesterol de los pacientes que han tenido un ataque cardíaco se reduce a medida que aumenta el tiempo desde su ataque cardíaco? Prueba al nivel 1%.
Paciente Nivel de colesterol Día 2 Nivel de colesterol Día 4 1 270 218 2 236 234 3 210 214 4 142 116 5 280 200 6 272 276 7 160 146 8 220 182 9 225 238 10 242 288 11 186 190 12 266 236 13 206 244 14 318 258 15 294 240 16 282 294 17 234 220 18 224 200 19 276 220 20 282 186 21 360 352 22 310 202 23 280 218 24 278 248 25 288 278 26 288 248 27 244 270 28 236 242 Tabla\(\PageIndex{4}\): Niveles de colesterol en (mg/dL) de pacientes con ataque cardíaco - El nivel de colesterol de los pacientes que presentaron ataques cardíacos se midió dos días después del ataque cardíaco y luego nuevamente cuatro días después del ataque cardíaco. Los investigadores quieren ver si el nivel de colesterol de los pacientes que tienen ataques cardíacos disminuye a medida que aumenta el tiempo transcurrido desde su ataque cardíaco. Los datos están en Ejemplo\(\PageIndex{4}\) (“Niveles de colesterol después”, 2013). Calcular un intervalo de confianza del 98% para la diferencia media en los niveles de colesterol del día dos al día cuatro.
- All Fresh Seafood es una empresa de pescado mayorista con sede en la costa este de los Estados Unidos Catalina Offshore Products es una empresa de pescado mayorista con sede en la costa oeste de Estados Unidos El ejemplo\(\PageIndex{5}\) contiene precios de ambas compañías para tipos específicos de pescado (“Seafood online”, 2013) (“Buy sushi grade”, 2013). ¿Los datos proporcionan evidencia suficiente para mostrar que un mayorista de peces de la costa oeste es más caro que un mayorista de la costa este? Prueba al nivel del 5%.
Pescados Todos los precios de mariscos frescos Precios de los productos Catalina Offshore Bacalao 19.99 17.99 Tilapi 6.00 13.99 Salmón de cultivo 19.99 22.99 Salmón Ecológico 24.99 24.99 Filete de Mero 29.99 19.99 Atún 28.99 31.99 Pez espada 23.99 23.99 Lubina 32.99 23.99 Bajo Rayado 29.99 14.99 Tabla\(\PageIndex{5}\): Precios Mayoristas de Pescado en Dólares - All Fresh Seafood es una empresa de pescado mayorista con sede en la costa este de los Estados Unidos Catalina Offshore Products es una empresa de pescado mayorista con sede en la costa oeste de Estados Unidos El ejemplo\(\PageIndex{5}\) contiene precios de ambas compañías para tipos específicos de pescado (“Seafood online”, 2013) (“Buy sushi grade”, 2013). Encuentre un intervalo de confianza del 95% para la diferencia media en el precio al por mayor entre los proveedores de la costa este y la costa oeste.
- El Departamento de Transporte británico estudió para ver si la gente evita conducir el viernes 13. Hicieron un recuento de tráfico un viernes y luego nuevamente un viernes 13 en las mismas dos ubicaciones (“Viernes 13”, 2013). Los datos para cada ubicación en las dos fechas diferentes se encuentran en Ejemplo\(\PageIndex{6}\). ¿Los datos muestran que en promedio menos personas conducen el viernes 13? Prueba al nivel del 5%.
Fechas 6to 13º 1990, julio 139246 138548 1990, julio 134012 132909 1991, septiembre 137055 136018 1991, septiembre 133732 131843 1991, diciembre 123552 121641 1991, diciembre 121139 118723 1992, marzo 128293 125532 1992, marzo 124631 120249 1992, noviembre 124609 122770 1992, noviembre 117584 117263 Tabla\(\PageIndex{6}\): Recuento de tráfico - El Departamento de Transporte británico estudió para ver si la gente evita conducir el viernes 13. Hicieron un recuento de tráfico un viernes y luego nuevamente un viernes 13 en las mismas dos ubicaciones (“Viernes 13”, 2013). Los datos para cada ubicación en las dos fechas diferentes se encuentran en Ejemplo\(\PageIndex{6}\). Estimar la diferencia media en el conteo de tráfico entre el 6 y el 13 usando un nivel de 90%.
- Para determinar si el Reiki es un método efectivo para tratar el dolor, se realizó un estudio piloto donde un terapeuta de Reiki certificado de segundo grado brindó tratamiento a voluntarios. El dolor se midió mediante una escala visual analógica (EVA) inmediatamente antes y después del tratamiento de Reiki (Olson & Hanson, 1997). Los datos están en Ejemplo\(\PageIndex{7}\). ¿Los datos muestran que el tratamiento con Reiki reduce el dolor? Prueba al nivel del 5%.
VAS antes VAS después 6 3 2 1 2 0 9 1 3 0 3 2 4 1 5 2 2 2 3 0 5 1 2 2 3 0 5 1 1 0 6 4 6 1 4 4 4 1 7 6 2 1 4 3 8 8 Tabla\(\PageIndex{7}\): Medidas del dolor antes y después del tratamiento de Reiki - Para determinar si el Reiki es un método efectivo para tratar el dolor, se realizó un estudio piloto donde un terapeuta de Reiki certificado de segundo grado brindó tratamiento a voluntarios. El dolor se midió mediante una escala visual analógica (EVA) inmediatamente antes y después del tratamiento de Reiki (Olson & Hanson, 1997). Los datos están en Ejemplo\(\PageIndex{7}\). Calcular un nivel de confianza del 90% para la diferencia media en la puntuación VAS antes y después del tratamiento con Reiki.
- Las tasas de participación femenina en la fuerza laboral (FLFPR) de las mujeres en países seleccionados al azar en 1990 y los últimos años de la década de 1990 están en Ejemplo\(\PageIndex{8}\) (Lim, 2002). ¿Los datos muestran que la tasa media de participación femenina en la fuerza laboral en 1990 es diferente de la de los últimos años de la década de 1990 utilizando un nivel de significación del 5%?
Región y país FLFPR 25-54 1990 FLFPR 25-54 Últimos años de la década de 1990 Irán 22.6 12.5 Marruecos 41.4 34.5 Catar 42.3 46.5 República Árabe Siria 25.6 19.5 Emiratos Árabes Unidos 36.4 39.7 Cabo Verde 46.7 50.9 Ghana 89.8 90.0 Kenia 82.1 82.6 Lesoto 51.9 68.0 Sudáfrica 54.7 61.7 Bangladesh 73.5 60.6 Malasia 49.0 50.2 Mongolia 84.7 71.3 Myanmar 72.1 72.3 Argentina 36.8 54 Belice 28.8 42.5 Bolivia 27.3 69.8 Brasil 51.1 63.2 Colombia 57.4 72.7 Ecuador 33.5 64 Nicaragua 50.1 42.5 Uruguay 59.5 71.5 Albania 77.4 78.8 Uzbekistán 79.6 82.8 Tabla\(\PageIndex{8}\): Tasas de Participación Femenina en Fuerza Laboral - Las tasas de participación femenina en la fuerza laboral de las mujeres en países seleccionados al azar en 1990 y los últimos años de la década de 1990 están en Ejemplo\(\PageIndex{8}\) (Lim, 2002). Estimar la diferencia media en la tasa de participación de la fuerza laboral femenina en 1990 a los últimos años de la década de 1990 utilizando un nivel de confianza del 95%?
- Ejemplo\(\PageIndex{9}\) contiene las frecuencias de pulso recolectadas de machos, que son no fumadores pero sí beben alcohol (“Pulso antes”, 2013). La frecuencia del pulso anterior es antes de que ejercitaran, y la frecuencia del pulso posterior se tomó después de que el sujeto corriera en su lugar durante un minuto. ¿Los datos indican que la frecuencia del pulso antes del ejercicio es menor que después del ejercicio? Prueba al nivel 1%.
Pulso antes Pulso después 76 88 56 110 64 126 50 90 49 83 68 136 68 125 88 150 80 146 78 168 59 92 60 104 65 82 76 150 145 155 84 140 78 141 85 131 78 132 Tabla\(\PageIndex{9}\): Frecuencia de pulso en machos antes y después del ejercicio - Ejemplo\(\PageIndex{9}\) contiene las frecuencias de pulso recolectadas de machos, que son no fumadores pero sí beben alcohol (“Pulso antes”, 2013). La frecuencia del pulso anterior es antes de que ejercitaran, y la frecuencia del pulso posterior se tomó después de que el sujeto corriera en su lugar durante un minuto. Calcular un intervalo de confianza del 98% para la diferencia media en las frecuencias del pulso antes y después del ejercicio.
- Responder
-
Para todas las pruebas de hipótesis, solo se da la conclusión. Para todos los intervalos de confianza, solo se da el intervalo usando la tecnología. Ver solución para toda la respuesta.
1. Rechazar Ho
2. \(5.39857 \mathrm{mg} / \mathrm{dL}<\mu_{d}<41.1729 \mathrm{mg} / \mathrm{dL}\)
3. No rechazar a Ho
4. \(-\$ 3.24216<\mu_{d}<\$ 8.13327\)
5. Rechazar Ho
6. \(1154.09<\mu_{d}<2517.51\)
7. Rechazar Ho
8. \(1.499<\mu_{d}<3.001\)
9. No rechazar a Ho
10. \(-10.9096 \%<\mu_{d}<0.2596 \%\)
11. Rechazar Ho
12. \(-62.0438 \text { beats/min }<\mu_{d}<-37.1141 \text { beats/min }\)


