9.3: Muestras independientes para dos medias
- Page ID
- 149710
En esta sección se analizará cómo analizar cuándo se recolectan dos muestras que son independientes. Al igual que con todas las demás pruebas de hipótesis e intervalos de confianza, el proceso es el mismo aunque las fórmulas y suposiciones son diferentes. La única diferencia con la prueba t independiente, a diferencia de las otras pruebas que se han hecho, es que en realidad hay dos fórmulas diferentes para usar dependiendo de si se cumple o no una suposición particular.
Prueba de hipótesis para prueba T independiente (prueba T de 2 muestras)
- Indicar las variables aleatorias y los parámetros en palabras.
\(x_{1}\)= variable aleatoria 1
\(x_{2}\) = variable aleatoria 2
\(\mu_{1}\) = media de la variable aleatoria 1
\(\mu_{2}\) = media de la variable aleatoria 2 - Declarar las hipótesis nulas y alternativas y el nivel de significación Las hipótesis normales serían
\(\begin{array}{ll}{H_{o} : \mu_{1}=\mu_{2}} & {\text { or } \quad H_{o} : \mu_{1}-\mu_{2}=0} \\ {H_{A} : \mu_{1}<\mu_{2}} & \quad\quad\: {H_{A} : \mu_{1}-\mu_{2}<0} \\ {H_{A} : \mu_{1}>\mu_{2}} & \quad\quad\: {H_{A} : \mu_{1}-\mu_{2}>0} \\ {H_{A} : \mu_{1} \neq \mu_{2}} & \quad\quad\: {H_{A} : \mu_{1}-\mu_{2} \neq 0}\end{array}\)
También, declara tu\(\alpha\) nivel aquí. - Indicar y verificar los supuestos para la prueba de hipótesis
- Se toma una muestra aleatoria\(n_{1}\) de tamaño de la población 1. Se toma una muestra aleatoria\(n_{2}\) de tamaño de la población 2.
Nota
No es necesario que las muestras sean del mismo tamaño, pero la prueba es más robusta si lo son.
- Las dos muestras son independientes.
- La población 1 se distribuye normalmente. La población 2 se distribuye normalmente. Al igual que antes, la prueba t es bastante robusta a la suposición de que el tamaño de la muestra es grande. Esto significa que si no se cumple esta suposición, pero los tamaños de sus muestras son bastante grandes (mayores de 30), entonces los resultados de la prueba t son válidos.
- Se desconocen las varianzas poblacionales y no se supone que sean iguales. El antiguo supuesto es que las varianzas son iguales. Sin embargo, esta suposición ya no es una suposición que la mayoría de los estadísticos utilizan. Esto se debe a que no es realmente realista asumir que las varianzas son iguales. Entonces simplemente asumiremos que es cierto el supuesto de que las varianzas son desconocidas y no asumidas que son iguales, y no se comprobará.
- Se toma una muestra aleatoria\(n_{1}\) de tamaño de la población 1. Se toma una muestra aleatoria\(n_{2}\) de tamaño de la población 2.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p Estadística de
muestra:
Calcular estadística de\(\overline{x}_{1}, \overline{x}_{2}, s_{1}, s_{2}, n_{1}, n_{2}\)
prueba:
Dado que la suposición que\(\sigma_{1}^{2}=\sigma_{2}^{2}\) no se está satisfaciendo, entonces
\(t=\dfrac{\left(\overline{x}_{1}-\overline{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\stackrel{s_{1}^{2}}{n_{1}}+\stackrel{s_{2}^{2}}{n_{2}}}}\)
Usualmente \(\mu_{1}-\mu_{2}=0\), desde\(H_{o} : \mu_{1}-\mu_{2}=0\)
Grados de libertad: (la ecuación Welch—Satterthwaite)
\(d f=\dfrac{(A+B)^{2}}{\dfrac{A^{2}}{n_{1}-1}+\dfrac{B^{2}}{n_{2}-1}}\)
donde\(A=\dfrac{s_{1}^{2}}{n_{1}} \text { and } B=\dfrac{s_{2}^{2}}{n_{2}}\)
p-valor:
Usando el TI-83/84: tcdf (límite inferior, límite superior, df)Usando R: pt (t, df)Nota
Si\(H_{A} : \mu_{1}-\mu_{2}<0\), entonces el límite inferior es\(-1 E 99\) y el límite superior es su estadística de prueba. Si\(H_{A} : \mu_{1}-\mu_{2}>0\), entonces el límite inferior es su estadística de prueba y el límite superior es\(1 E 99\). Si\(H_{A} : \mu_{1}-\mu_{2} \neq 0\), entonces encuentra el valor p para\(H_{A} : \mu_{1}-\mu_{2}<0\), y multiplica por 2.
Nota
Si\(H_{A} : \mu_{1}-\mu_{2}<0\), entonces usa pt (t, df). Si\(H_{A} : \mu_{1}-\mu_{2}>0\), entonces usa 1 - pt (t, df). Si\(H_{A} : \mu_{1}-\mu_{2} \neq 0\), entonces encuentra el valor p para\(H_{A} : \mu_{1}-\mu_{2}<0\), y multiplica por 2.
- Conclusión
Aquí es donde escribes rechazar\(H_{o}\) o no rechazar\(H_{o}\). La regla es: si el valor p <\(\alpha\), entonces rechazar\(H_{o}\). Si el valor p\(\geq \alpha\), entonces no puede rechazar\(H_{o}\) - Interpretación Aquí es donde interpretas en términos del mundo real la conclusión a la prueba. La conclusión para una prueba de hipótesis es que o bien tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad, o no tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad.
Intervalo de confianza para la diferencia en medias de dos muestras independientes (2 Samp T-Int)
El intervalo de confianza para la diferencia en medias tiene las mismas variables y medias aleatorias y los mismos supuestos que la prueba de hipótesis para muestras independientes. Si ya has completado la prueba de hipótesis, entonces no necesitas declararlas nuevamente. Si no ha completado la prueba de hipótesis, entonces indique las variables y medias aleatorias y el estado y verifique los supuestos antes de completar el paso del intervalo de confianza.
- Encuentre el estadístico de muestra y el intervalo de confianza Estadística de
muestra:
Calcular Intervalo de Confianza:\(\overline{x}_{1}, \overline{x}_{2}, s_{1}, s_{2}, n_{1}, n_{2}\)
La estimación del intervalo de confianza de la diferencia es\(\mu_{1}-\mu_{2}\)
Dado que la suposición que\(\sigma_{1}^{2}=\sigma_{2}^{2}\) no se está satisfaciendo, entonces
\(\left(\overline{x}_{1}-\overline{x}_{2}\right)-E<\mu_{1}-\mu_{2}<\left(\overline{x}_{1}-\overline{x}_{2}\right)+E\)
\(E=t_{c} \sqrt{\dfrac{s_{1}^{2}}{n_{1}}+\dfrac{s_{2}^{2}}{n_{2}}}\)
dónde\(t_{c}\) está el valor crítico con grados de libertad:
Grados de libertad: (la ecuación Welch—Satterthwaite)
\(d f=\dfrac{(A+B)^{2}}{\dfrac{A^{2}}{n_{1}-1}+\dfrac{B^{2}}{n_{2}-1}}\)
donde\(A=\dfrac{s_{1}^{2}}{n_{1}} \text { and } B=\dfrac{s_{2}^{2}}{n_{2}}\) - Interpretación estadística: En general esto parece, “hay una probabilidad de C% que\(\left(\overline{x}_{1}-\overline{x}_{2}\right)-E<\mu_{1}-\mu_{2}<\left(\overline{x}_{1}-\overline{x}_{2}\right)+E\) contiene la verdadera diferencia de medias”.
- Interpretación del Mundo Real: Aquí es donde declaras qué intervalo contiene la verdadera diferencia de medias, aunque a menudo declaras cuánto más (o menos) es la primera media de la segunda media.
El valor crítico es un valor de la distribución t de Student. Dado que se encuentra un intervalo de confianza sumando y restando un margen de cantidad de error de la diferencia en las medias de la muestra, y el intervalo tiene una probabilidad de contener la verdadera diferencia en medias, entonces se puede pensar en esto como la declaración\(P\left(\left(\overline{x}_{1}-\overline{x}_{2}\right)-E<\mu_{1}-\mu_{2}<\left(\overline{x}_{1}-\overline{x}_{2}\right)+E\right)=C\). Para encontrar el valor crítico se utiliza la tabla A.2 en el Apéndice.
Cómo verificar los supuestos de la prueba t de dos muestras y el intervalo de confianza:
Para que la prueba t o el intervalo de confianza sean válidos, los supuestos de la prueba deben ser ciertos. Entonces, siempre que ejecutes una prueba t o un intervalo de confianza, debes asegurarte de que las suposiciones sean verdaderas. Por lo que hay que revisarlos. Así es como haces esto:
- Para la suposición de muestra aleatoria, describa cómo tomó las dos muestras. Asegúrese de que su técnica de muestreo sea aleatoria para ambas muestras.
- Para el supuesto independiente, describa cómo son muestras independientes.
- Para el supuesto de que cada población se distribuya normalmente, recuerde el proceso de evaluación de la normalidad del capítulo 6. Asegúrese de evaluar cada muestra por separado.
- No es necesario verificar la suposición de igual varianza ya que no se está asumiendo.
Ejemplo\(\PageIndex{1}\) hypothesis test for two means
El nivel de colesterol de los pacientes que presentaron ataques cardíacos se midió dos días después del ataque cardíaco. Los investigadores quieren ver si los pacientes que tienen ataques cardíacos tienen niveles de colesterol más altos que las personas sanas, por lo que también midieron el nivel de colesterol de adultos sanos que no muestran signos de enfermedad cardíaca. Los datos están en Tabla\(\PageIndex{1}\) (“Niveles de colesterol después”, 2013). ¿Los datos muestran que las personas que han tenido ataques cardíacos tienen niveles más altos de colesterol sobre los pacientes que no han tenido ataques cardíacos? Prueba al nivel 1%.
| Nivel de colesterol en pacientes con ataque cardíaco | Nivel de colesterol del individuo sano |
|---|---|
| 270 | 196 |
| 236 | 232 |
| 210 | 200 |
| 142 | 242 |
| 280 | 206 |
| 272 | 178 |
| 160 | 184 |
| 220 | 198 |
| 226 | 160 |
| 242 | 182 |
| 186 | 182 |
| 266 | 198 |
| 206 | 182 |
| 318 | 238 |
| 294 | 198 |
| 282 | 188 |
| 234 | 166 |
| 224 | 204 |
| 276 | 182 |
| 282 | 178 |
| 360 | 212 |
| 310 | 164 |
| 280 | 230 |
| 278 | 186 |
| 288 | 162 |
| 288 | 182 |
| 244 | 218 |
| 236 | 170 |
| 200 | |
| 176 |
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar las hipótesis nulas y alternativas y el nivel de significación.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
- Conclusión
- Interpretación
Solución
1. \(x_{1}\)= Nivel de colesterol en pacientes que tuvieron un ataque al corazón
\(x_{2}\)= Nivel de colesterol en individuos sanos
\(\mu_{1}\)= nivel medio de colesterol de los pacientes que tuvieron un ataque al corazón
\(\mu_{2}\)= nivel medio de colesterol de individuos sanos
2. Las hipótesis normales serían
\(\begin{array}{ll}{H_{o} : \mu_{1}=\mu_{2}} & {\text { or } \quad H_{o} : \mu_{1}-\mu_{2}=0} \\ {H_{A} : \mu_{1}>\mu_{2}} & \quad\quad\:{H_{A} : \mu_{1}-\mu_{2}>0} \\ {\alpha=0.01}\end{array}\)
3.
- Se toma una muestra aleatoria de 28 niveles de colesterol de pacientes que tuvieron un ataque cardíaco. Se toma una muestra aleatoria de 30 niveles de colesterol de individuos sanos. El problema no indica si alguna de las muestras fue seleccionada aleatoriamente. Por lo que esta suposición puede no ser válida.
- Las dos muestras son independientes. Esto se debe a que o estaban tratando con pacientes que presentaban ataques cardíacos o individuos sanos.
- La población de todos los niveles de colesterol de los pacientes que tuvieron un ataque cardíaco se distribuye normalmente. La población de todos los niveles de colesterol de individuos sanos se distribuye normalmente.
Pacientes que tuvieron ataques cardíacos:
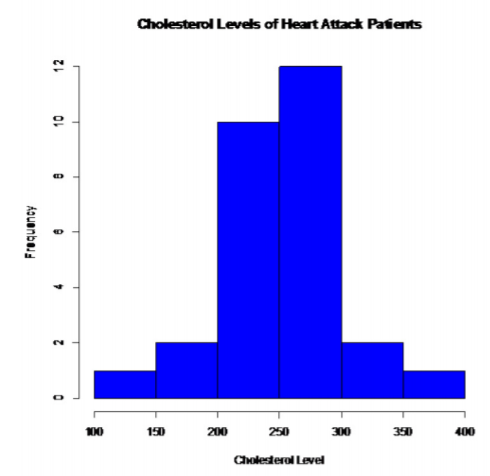.png)
Esto se ve algo en forma de campana.
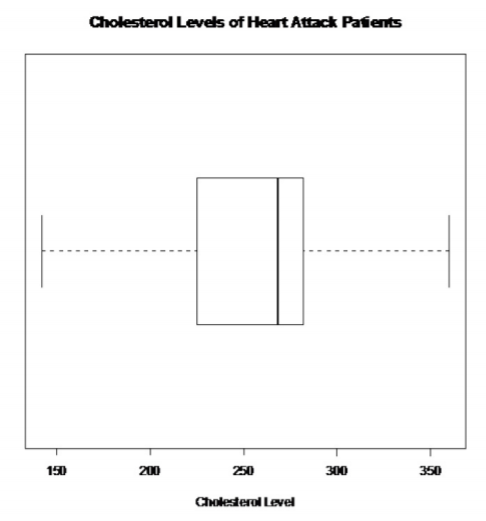.png)
No hay valores atípicos
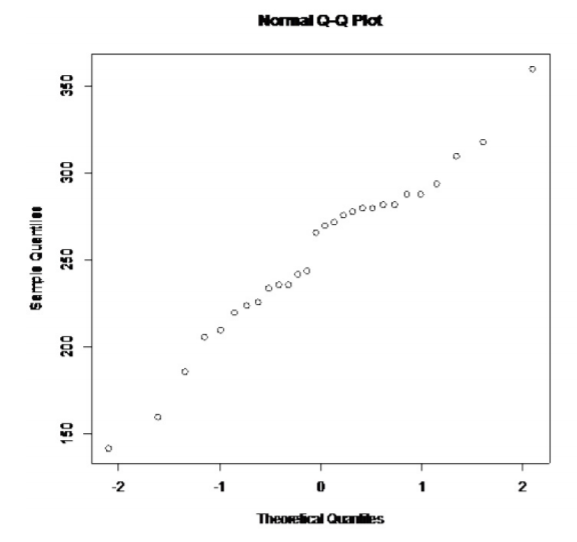.png)
Esto se ve algo lineal.
Entonces, la población de todos los niveles de colesterol de los pacientes que tuvieron ataques cardíacos probablemente esté algo distribuida normalmente.
Individuos sanos:
.png)
Esto no parece en forma de campana.
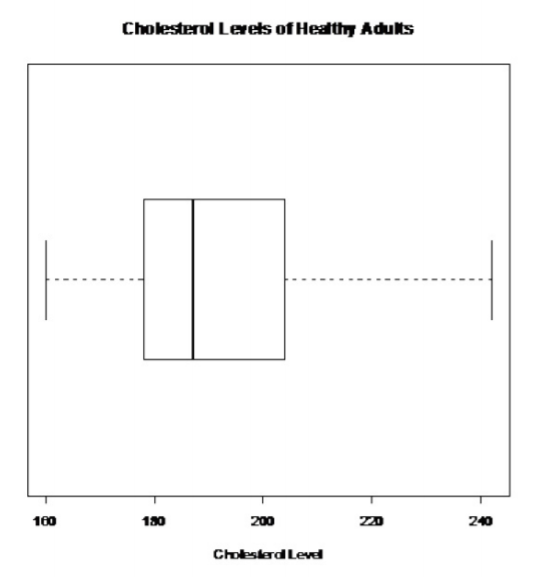.png)
No hay valores atípicos.
.png)
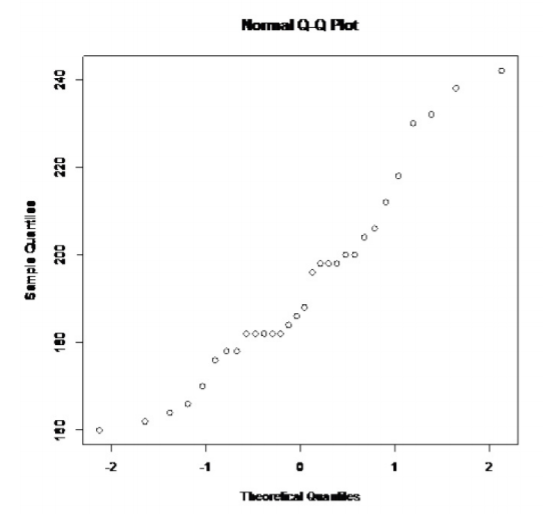
Esto no parece lineal.
Entonces, la población de todos los niveles de colesterol de individuos sanos probablemente no se distribuya normalmente.
Esta suposición no es válida para la segunda muestra. Dado que la muestra es bastante grande y la prueba t es robusta, puede que no sea un problema. No obstante, solo hay que darse cuenta de que las conclusiones de la prueba pueden no ser válidas.
4. Estadística de muestra:
\(\overline{x}_{1} \approx 252.32, \overline{x}_{2} \approx 193.13, s_{1} \approx 47.0642, s_{2} \approx 22.3000, n_{1}=28, n_{2}=30\)
Estadística de prueba:
\(t=\dfrac{\left(\overline{x}_{1}-\overline{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\dfrac{s_{1}^{2}}{n_{1}}+\dfrac{s_{2}^{2}}{n_{2}}}}\)
\(=\dfrac{(252.32-193.13)-0}{\sqrt{\dfrac{47.0642^{2}}{28}+\dfrac{22.3000^{2}}{30}}}\)
\(\approx 6.051\)
Grados de libertad: (la ecuación Welch-Satterthwaite)
\(A=\dfrac{s_{1}^{2}}{n_{1}}=\dfrac{47.0642^{2}}{28} \approx 79.1085\)
\(B=\dfrac{s_{2}^{2}}{n_{2}}=\dfrac{22.3000^{2}}{30} \approx 16.5763\)
\(d f=\dfrac{(A+B)^{2}}{\dfrac{A^{2}}{n_{1}-1}+\dfrac{B^{2}}{n_{2}-1}}=\dfrac{(79.1085+16.5763)^{2}}{\dfrac{79.1085^{2}}{28-1}+\dfrac{16.5763^{2}}{30-1}} \approx 37.9493\)
valor p:
Usando TI-83/84:\(\operatorname{tcdf}(6.051,1 E 99,37.9493) \approx 2.44 \times 10^{-7}\)
Usando R:\(1-\mathrm{pt}(6.051,37.9493) \approx 2.44 \times 10^{-7}\)
Uso de la Tecnología: Usando el TI-83/84:
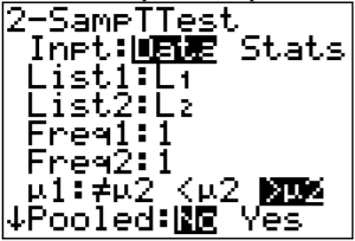.png)
Nota
La pregunta agrupada en la calculadora es para saber si estás asumiendo que las varianzas son iguales. Como no se está haciendo esta suposición, entonces la respuesta a esta pregunta es no. En conjunto significa que usted asume que las varianzas son iguales y puede agrupar las varianzas de la muestra juntas.
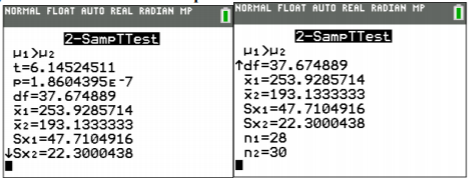.png)
Usando R: comando en general: t.test (variable1, variable2, alternativa = “menos” o “mayor”)
Para este ejemplo, el comando R es:
t.test (ataque al corazón, saludable, alternative="mayor”)
Prueba t de dos muestras de Welch
datos: ataque al corazón y saludable
t = 6.1452, df = 37.675, valor p = 1.86e-07
hipótesis alternativa: la verdadera diferencia en medias es mayor que 0
Intervalo de confianza del 95 por ciento:
44.1124 Inf
estimaciones de la muestra:
media de x media de y
253.9286 193.1333
El estadístico de prueba es t = 6.1452. El valor p es\(1.86 \times 10^{-7}\)
5. Rechazar\(H_{o}\) desde el valor p <\(\alpha\).
6. Esto es evidencia suficiente para mostrar que los pacientes que han tenido ataques cardíacos tienen un nivel de colesterol más alto en promedio de individuos sanos. (Aunque se den cuenta de que algunos de los supuestos no son válidos, por lo que esta interpretación puede ser inválida.)
Ejemplo\(\PageIndex{2}\) confidence interval for \(\mu_{1}-\mu_{2}\)
El nivel de colesterol de los pacientes que presentaron ataques cardíacos se midió dos días después del ataque cardíaco. Los investigadores quieren ver si los pacientes que tienen ataques cardíacos tienen niveles de colesterol más altos que las personas sanas, por lo que también midieron el nivel de colesterol de adultos sanos que no muestran signos de enfermedad cardíaca. Los datos están en Ejemplo\(\PageIndex{1}\) (“Niveles de colesterol después”, 2013). Encuentre un intervalo de confianza del 99% para la diferencia media en los niveles de colesterol entre pacientes con ataque cardíaco e individuos sanos.
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentra el estadístico muestral y el intervalo de confianza.
- Interpretación Estadística
- Interpretación del mundo real
Solución
1. Estos fueron declarados en Ejemplo\(\PageIndex{1}\), pero se reproducen aquí como referencia.
\(x_{1}\)= Nivel de colesterol en pacientes que tuvieron un ataque al corazón
\(x_{2}\)= Nivel de colesterol en individuos sanos
\(\mu_{1}\)= nivel medio de colesterol de los pacientes que tuvieron un ataque al corazón
\(\mu_{2}\)= nivel medio de colesterol de individuos sanos
2. Los supuestos fueron declarados y comprobados en Ejemplo\(\PageIndex{1}\).
3. Estadística de muestra:
\(\overline{x}_{1} \approx 252.32, \overline{x_{2}} \approx 193.13, s_{1} \approx 47.0642, s_{2} \approx 22.3000, n_{1}=28, n_{2}=30\)
Estadística de prueba:
Grados de libertad: (la ecuación Welch—Satterthwaite)
\(A=\dfrac{s_{1}^{2}}{n_{1}}=\dfrac{47.0642^{2}}{28} \approx 79.1085\)
\(B=\dfrac{s_{2}^{2}}{n_{2}}=\dfrac{22.3000^{2}}{30} \approx 16.5763\)
\(d f=\dfrac{(A+B)^{2}}{\dfrac{A^{2}}{n_{1}-1}+\dfrac{B^{2}}{n_{2}-1}}=\dfrac{(79.1085+16.5763)^{2}}{\dfrac{79.1085^{2}}{28-1}+\dfrac{16.5763^{2}}{30-1}} \approx 37.9493\)
Ya que este df no está en la mesa, redondo al número entero más cercano.
\(t_{c}=2.712\)
\(E=t_{c} \sqrt{\dfrac{s_{1}^{2}}{n_{1}}+\dfrac{s_{2}^{2}}{n_{2}}}=2.712 \sqrt{\dfrac{47.0642^{2}}{28}+\dfrac{22.3000^{2}}{30}} \approx 26.53\)
\(\left(\overline{x}_{1}-\overline{x}_{2}\right)-E<\mu_{1}-\mu_{2}<\left(\overline{x}_{1}-\overline{x}_{2}\right)+E\)
\((252.32-193.13)-26.53<\mu_{1}-\mu_{2}<(252.32-193.13)+26.53\)
\(32.66 \mathrm{mg} / \mathrm{dL}<\mu_{1}-\mu_{2}<85.72 \mathrm{mg} / \mathrm{dL}\)
Uso de la Tecnología:
Usando TI-83/84:
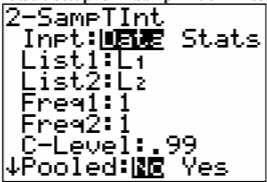.png)
Nota
La pregunta agrupada en la calculadora es para saber si estás asumiendo que las varianzas son iguales. Como no se está haciendo esta suposición, entonces la respuesta a esta pregunta es no. En conjunto significa que usted asume que las varianzas son iguales y puede agrupar las varianzas de la muestra juntas.
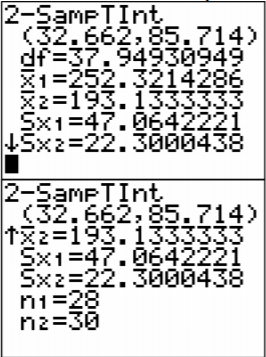.png)
Usando R: los comandos son t.test (variable1, variable2, conf.level=C), donde C está en forma decimal.
Para este ejemplo, el comando es
t.test (infarto, saludable, conf.level=.99)
Salida:
Prueba t de dos muestras de Welch
datos: ataque al corazón y saludable
t = 6.1452, df = 37.675, valor p = 3.721e-07
hipótesis alternativa: la verdadera diferencia en medias no es igual a 0
Intervalo de confianza del 99 por ciento:
33.95750 87.63298
estimaciones de la muestra:
media de x media de y
253.9286 193.1333
El intervalo de confianza es\(33.96<\mu_{1}-\mu_{2}<87.63\)
4. Hay un 99% de probabilidad que\(33.96<\mu_{1}-\mu_{2}<87.63\) contenga la verdadera diferencia de medias.
5. El nivel medio de colesterol para los pacientes que tuvieron ataques cardíacos es de 32.66 mg/dL a 85,72 mg/dL más que el nivel medio de colesterol para pacientes sanos. (Aunque se den cuenta de que muchos de los supuestos no son válidos, por lo que esta interpretación puede ser inválida.)
Si asumes que las varianzas son iguales, es decir\(\sigma_{1}^{2}=\sigma_{2}^{2}\), entonces el estadístico de prueba es:
\(t=\dfrac{\left(\overline{x}_{1}-\overline{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{s_{p} \sqrt{\dfrac{1}{n_{1}}+\dfrac{1}{n_{2}}}}\)
donde\(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{\left(n_{1}-1\right)+\left(n_{2}-1\right)}}\)
\(s_{p}\)= desviación estándar agrupada
Los Grados de Libertad es: df =\(n_{1}+n_{2}-2\)
El intervalo de confianza si asumes que se\(\sigma_{1}^{2}=\sigma_{2}^{2}\) ha cumplido, es
\(\left(\overline{x}_{1}-\overline{x}_{2}\right)-E<\mu_{1}-\mu_{2}<\left(\overline{x}_{1}-\overline{x}_{2}\right)+E\)
donde\(E=t_{c} s_{p} \sqrt{\dfrac{1}{n_{1}}+\dfrac{1}{n_{2}}}\)
y\(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{\left(n_{1}-1\right)+\left(n_{2}-1\right)}}\)
Grados de Libertad: df =\(n_{1}+n_{2}-2\)
\(t_{c}\)es el valor crítico donde C = 1 -\(\alpha\)
Para demostrar que las varianzas son iguales, solo demuestre que la relación de las varianzas de su muestra no es inusual (la probabilidad es mayor a 0.05). En otras palabras, asegúrate de que lo siguiente sea cierto.
\(P\left(F>s_{1}^{2} / s_{2}^{2}\right) \geq 0.05\left(\text { or } P\left(F>s_{2}^{2} / s_{1}^{2}\right) \geq 0.05\right.\)para que la varianza mayor esté en el numerador). Esta probabilidad es de una distribución F. Para encontrar la probabilidad en el uso de la calculadora TI-83/84\(\operatorname{Fcdf}\left(s_{1}^{2} / s_{2}^{2}, 1 E 99, n_{1}-1, n_{2}-1\right)\). Para encontrar la probabilidad sobre R, use\(1-\operatorname{pf}\left(s_{1}^{2} / s_{2}^{2}, n_{1}-1, n_{2}-1\right)\).
Nota
La distribución F es muy sensible a la distribución normal. Una mejor prueba para varianzas iguales es la prueba de Levene, aunque es más complicada. Lo mejor es hacer la prueba de Levene cuando se usa software estadístico (como SPSS o Minitab) para realizar la prueba t independiente de dos muestras.
Ejemplo\(\PageIndex{3}\) hypothesis test for two means
Se midió la cantidad de sodio en los hotdogs de carne. Además, también se midió la cantidad de sodio en perritos de aves de corral (“SOCR 012708 id”, 2013). Los datos están en Ejemplo\(\PageIndex{2}\). ¿Hay pruebas suficientes para demostrar que la carne de res tiene menos sodio en promedio que los perritos de aves de corral? Utilizar un nivel de significancia del 5%.
| Sodio en Perritos Calientes de Carne | Sodio en Perros Calientes Avícolas |
|---|---|
| 495 | 430 |
| 477 | 375 |
| 425 | 396 |
| 322 | 383 |
| 482 | 387 |
| 587 | 542 |
| 370 | 359 |
| 322 | 357 |
| 479 | 528 |
| 375 | 513 |
| 330 | 426 |
| 300 | 513 |
| 386 | 358 |
| 401 | 581 |
| 645 | 588 |
| 440 | 522 |
| 317 | 545 |
| 319 | 430 |
| 298 | 375 |
| 253 | 396 |
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar las hipótesis nulas y alternativas y el nivel de significación.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentre el estadístico de muestra, el estadístico de prueba y el valor p.
- Conclusión
- Interpretación
Solución
1. \(x_{1}\)= nivel de sodio en perritos de carne
\(x_{2}\)= nivel de sodio en perritos de aves
\(\mu_{1}\)= nivel medio de sodio en perritos de carne
\(\mu_{2}\)= nivel medio de sodio en perritos de aves
2. Las hipótesis normales serían
\(\begin{array}{ll}{H_{o} : \mu_{1}=\mu_{2}} & {\text { or } \quad H_{o} : \mu_{1}-\mu_{2}=0} \\ {H_{A} : \mu_{1}<\mu_{2}} & \quad\quad\: {H_{A} : \mu_{1}-\mu_{2}<0} \\ {\alpha=0.05}\end{array}\)
3.
- Se toma una muestra aleatoria de 20 niveles de sodio en hotdogs de carne. Una muestra aleatoria de 20 niveles de sodio en perritos de aves de corral. El problema no indica si alguna de las muestras fue seleccionada aleatoriamente. Por lo que esta suposición puede no ser válida.
- Las dos muestras son independientes ya que se trata de diferentes tipos de hotdogs.
- La población de todos los niveles de sodio en los hotdogs de carne se distribuye normalmente. La población de todos los niveles de sodio en perritos de aves de corral se distribuye normalmente. Perritos Calientes de Carne:
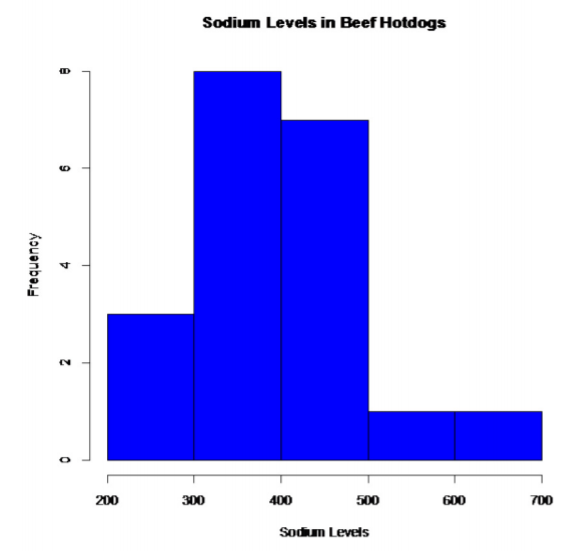.png)
Esto se ve algo en forma de campana.
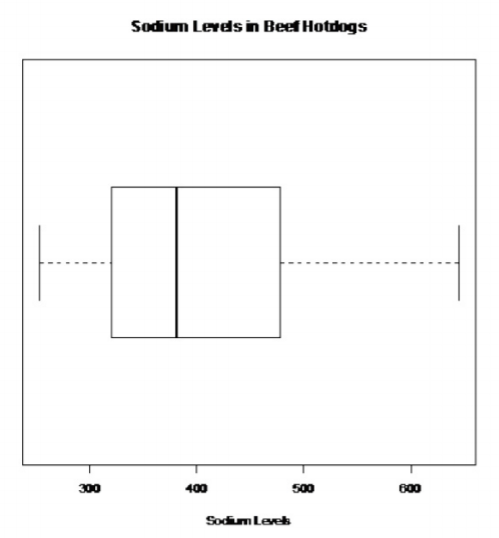.png)
No hay valores atípicos.
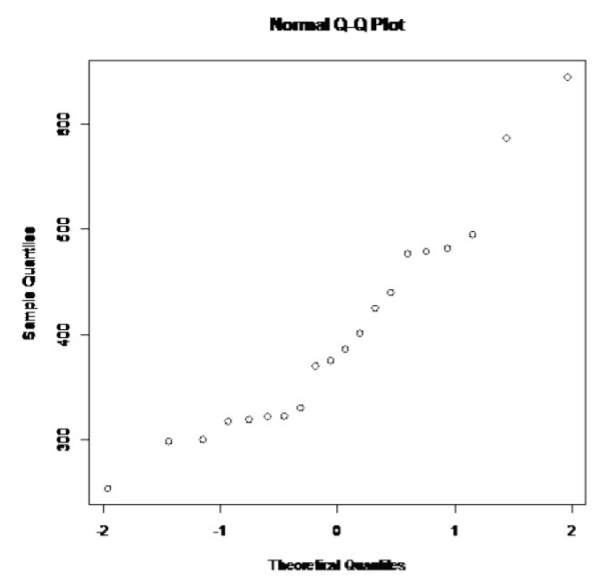.png)
Esto se ve algo lineal.
Entonces, la población de todos los niveles de sodio en los hotdogs de carne puede distribuirse normalmente.
Perros Calientes Avícolas:
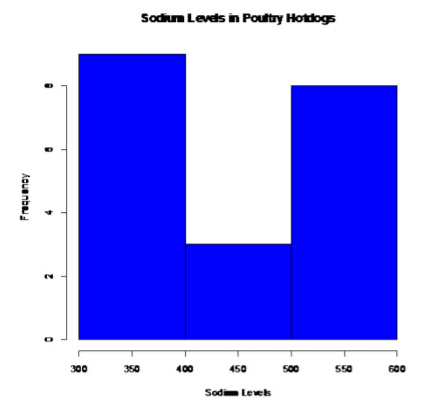.png)
Esto no parece en forma de campana.
.png)
No hay valores atípicos.
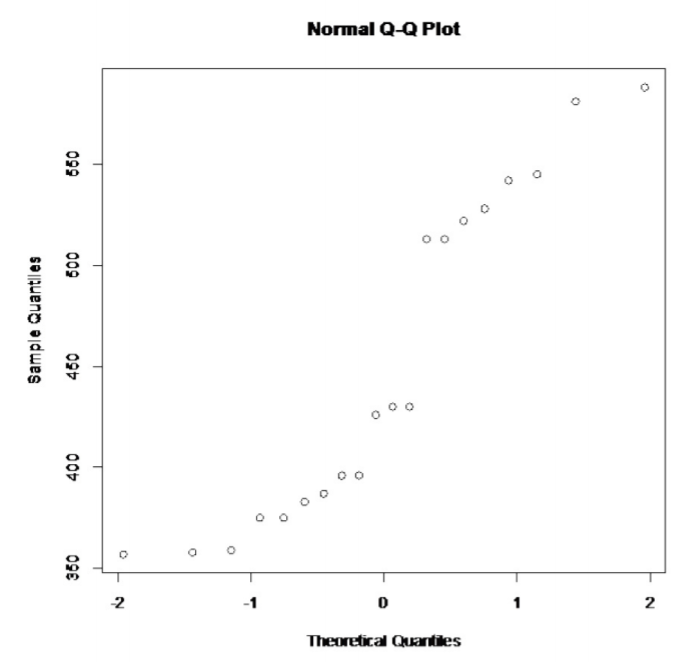.png)
Esto no parece lineal.
Entonces, la población de todos los niveles de sodio en los perritos de aves de corral probablemente no se distribuya normalmente.
Esta suposición no es válida. Dado que las muestras son bastante grandes y la prueba t es robusta, puede que no sea un problema grande. No obstante, solo hay que darse cuenta de que las conclusiones de la prueba pueden no ser válidas.
d. Las varianzas poblacionales son iguales, es decir\(\sigma_{1}^{2}=\sigma_{2}^{2}\).
\(\begin{array}{l}{s_{1} \approx 102.4347} \\ {s_{2} \approx 81.1786} \\ {\dfrac{s_{1}^{2}}{s_{2}^{2}}=\dfrac{102.4347^{2}}{81.1786^{2}} \approx 1.592}\end{array}\)
Usando TI-83/84: Fcdf\((1.592,1 E 99,19,19) \approx 0.1597 \geq 0.05\)
Usando R: 1 - pf\((1.592,19,19) \approx 0.1597 \geq 0.05\)
Entonces se puede decir que estas varianzas son iguales.
4. Encuentre el estadístico de muestra, el estadístico de prueba y el valor p
Estadística de muestra:
\(\overline{x}_{1}=401.15, \overline{x}_{2}=450.2, s_{1} \approx 102.4347, s_{2} \approx 81.1786, n_{1}=20, n_{2}=20\)
Estadística de prueba:
Se\(\sigma_{1}^{2}=\sigma_{2}^{2}\) ha cumplido la suposición, por lo que
\(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{\left(n_{1}-1\right)+\left(n_{2}-1\right)}}\)
\(=\sqrt{\dfrac{102.4347^{2} * 19+81.1786^{2} * 19}{(20-1)+(20-1)}}\)
\(\approx 92.4198\)
Aunque deberías intentar hacer los cálculos en el problema para no crear un error de redondeo.
\(t=\dfrac{\left(\overline{x}_{1}-\overline{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{s_{P} \sqrt{\dfrac{1}{n_{1}}+\dfrac{1}{n_{2}}}}\)
\(=\dfrac{(401.15-450.2)-0}{92.4198 \sqrt{\dfrac{1}{20}+\dfrac{1}{20}}}\)
\(\approx-1.678\)
df = 20 + 20 - 2 = 38
valor p:
Usando TI-83/84: tcdf\((-1 E 99,-1.678,38) \approx 0.0508\)
Usando R: pt\((-1.678,38) \approx 0.0508\)
Usando la tecnología para encontrar el valor t y p:
Usando TI-83/84:
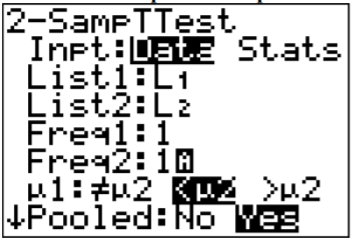.png)
Nota
La pregunta agrupada en la calculadora es para saber si está utilizando la desviación estándar agrupada o no. En este ejemplo, se utilizó la desviación estándar agrupada ya que está asumiendo que las varianzas son iguales. Por eso la respuesta a la pregunta es Sí.
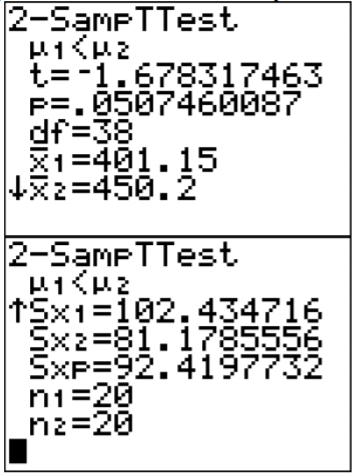.png)
Usando R: el comando es t.test (variable1, variable2, alternative="less” o “mayor”)
Para este ejemplo, el comando es
t.test (carne de res, aves de corral, alternativa="less”, equalvar=true)
Prueba t de dos muestras de Welch
datos: carne de res y aves
t = -1.6783, df = 36.115, valor p = 0.05096
hipótesis alternativa: la verdadera diferencia en las medias es menor que 0
Intervalo de confianza del 95 por ciento:
-Inf 0.2875363
estimaciones de la muestra:
media de x media de y
401.15 450.20
El t = -1.6783 y el valor p = 0.05096.
5. No se puede rechazar\(H_{o}\) ya que el valor p >\(\alpha\).
6. Esto no es evidencia suficiente para demostrar que los hotdogs de carne tienen menos sodio que los perritos de aves de corral. (Aunque se den cuenta de que muchos de los supuestos no son válidos, por lo que esta interpretación puede ser inválida.)
Ejemplo\(\PageIndex{4}\) confidence interval for \(\mu_{1}-\mu_{2}\)
Se midió la cantidad de sodio en los hotdogs de carne. Además, también se midió la cantidad de sodio en perritos de aves de corral (“SOCR 012708 id”, 2013). Los datos están en Ejemplo\(\PageIndex{2}\). Encuentre un intervalo de confianza del 95% para la diferencia media en los niveles de sodio entre los perritos de carne y aves de corral.
- Indicar las variables aleatorias y los parámetros en palabras.
- Indicar y verificar los supuestos para la prueba de hipótesis.
- Encuentra el estadístico muestral y el intervalo de confianza.
- Interpretación Estadística
- Interpretación del mundo real
Solución
1. Estos fueron declarados en Ejemplo\(\PageIndex{1}\), pero se reproducen aquí como referencia.
\(x_{1}\)= nivel de sodio en perritos de carne
\(x_{2}\)= nivel de sodio en perritos de aves
\(\mu_{1}\)= nivel medio de sodio en perritos de carne
\(\mu_{2}\)= nivel medio de sodio en perritos de aves
2. Los supuestos fueron declarados y comprobados en Ejemplo\(\PageIndex{3}\).
3. Estadística de muestra:
\(\overline{x}_{1}=401.15, \overline{x}_{2}=450.2, s_{1} \approx 102.4347, s_{2} \approx 81.1786, n_{1}=20, n_{2}=20\)
Intervalo de confianza:
La estimación del intervalo de confianza de la diferencia\(\mu_{1}-\mu_{2}\) es
Se\(\sigma_{1}^{2}=\sigma_{2}^{2}\) ha cumplido la suposición, por lo que
\(s_{p}=\sqrt{\dfrac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{\left(n_{1}-1\right)+\left(n_{2}-1\right)}}\)
\(=\sqrt{\dfrac{102.4347^{2} * 19+81.1786^{2} * 19}{(20-1)+(20-1)}}\)
\(\approx 92.4198\)
Aunque deberías intentar hacer los cálculos en la fórmula para E para no crear un error de redondeo.
df =\(=n_{1}+n_{2}-2=20+20-2=38\)
\(t_{c} = 2.024\)
\(E=t_{c} s_{p} \sqrt{\dfrac{1}{n_{1}}+\dfrac{1}{n_{2}}}\)
\(=2.024(92.4198) \sqrt{\dfrac{1}{20}+\dfrac{1}{20}}\)
\(\approx 59.15\)
\(\left(\overline{x}_{1}-\overline{x}_{2}\right)-E<\mu_{1}-\mu_{2}<\left(\overline{x}_{1}-\overline{x}_{2}\right)+E\)
\((401.15-450.2)-59.15<\mu_{1}-\mu_{2}<(401.15-450.2)+59.15\)
\(-108.20 \mathrm{g}<\mu_{1}-\mu_{2}<10.10 \mathrm{g}\)
Uso de la tecnología:
Usando el TI-83/84:
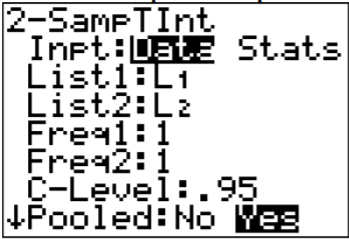.png)
Nota
La pregunta agrupada en la calculadora es para saber si está utilizando la desviación estándar agrupada o no. En este ejemplo, se utilizó la desviación estándar agrupada ya que está asumiendo que las varianzas son iguales. Por eso la respuesta a la pregunta es Sí.
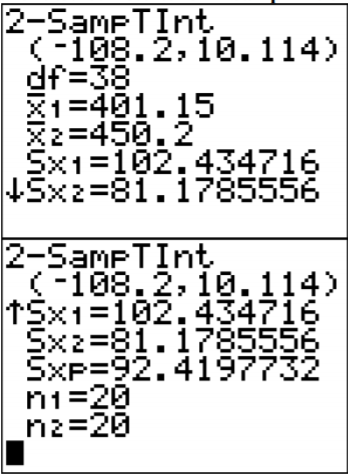.png)
Usando R: el comando es t.test (variable1, variable2, equalvar=true, conf.level=C), donde C está en forma decimal.
Para este ejemplo, el comando es
t.test (carne de res, aves de corral, conf.level=.95, EqualVar=true)
Prueba t de dos muestras de Welch
datos: carne de res y aves
t = -1.6783, df = 36.115, valor p = 0.1019
hipótesis alternativa: la verdadera diferencia en medias no es igual a 0
Intervalo de confianza del 95 por ciento:
-108.31592 10.21592
estimaciones de la muestra:
media de x media de y
401.15 450.20
El intervalo de confianza es\(-108.32<\mu_{1}-\mu_{2}<10.22\).
4. Hay un 95% de probabilidad que\(-108.20 \mathrm{g}<\mu_{1}-\mu_{2}<10.10 \mathrm{g}\) contenga la verdadera diferencia de medias.
5. El nivel medio de sodio de los hotdogs de carne es de 108.20 g menos que el nivel medio de sodio de los hotdogs de aves de corral a 10.10 g más. (El signo negativo en el límite inferior implica que la primera media es menor que la segunda media. El signo positivo en el límite superior implica que la primera media es mayor que la segunda media).
Darse cuenta que muchos de los supuestos no son válidos en este ejemplo, por lo que la interpretación puede ser inválida.
Tareas
Ejercicio\(\PageIndex{1}\)
En cada problema se muestran todos los pasos de la prueba de hipótesis o intervalo de confianza. Si no se cumplen algunos de los supuestos, tenga en cuenta que los resultados de la prueba o intervalo pueden no ser correctos y luego continuar el proceso de la prueba de hipótesis o intervalo de confianza. A menos que lo indique su instructor, no asuma que las varianzas son iguales (excepto en los problemas del 11 al 16).
- Los ingresos de los varones en cada estado de Estados Unidos, incluyendo el Distrito de Columbia y Puerto Rico, se dan en Ejemplo\(\PageIndex{3}\), y los ingresos de las mujeres se dan en la tabla #9 .3.4 (“Ingresos medios de,” 2013). ¿Hay pruebas suficientes para demostrar que el ingreso medio de los hombres es mayor que el de las mujeres? Prueba al nivel 1%.
42,951 52,379 $42,544 37,488 49,281 50,987 60,705 50,411 66,760 $40,951 $43,902 45,494 41,528 50,746 $45,183 $43,624 $43,993 41,612 46,313 $43,944 56,708 60,264 50,053 50,580 $40,202 $43,146 41,635 $42,182 $41,803 53,033 60,568 41,037 50,388 $41,950 $44,660 46,176 41,420 45,976 $47,956 22,529 48,842 $41,464 $40,285 41,309 $43,160 47,573 $44,057 52,805 53,046 $42,125 46,214 51,630 Tabla\(\PageIndex{3}\): Datos de Ingresos para Varones $31,862 $40,550 36,048 30,752 41,817 $40,236 47,476 $40,500 $60,332 $33,823 $35,438 37,242 $31,238 $39,150 34,023 $33,745 $33,269 $32,684 $31,844 34,599 48,748 46,185 $36,931 $40,416 29,548 $33,865 $31,067 $33,424 35,484 41,021 $47,155 $32,316 $42,113 $33,459 $32,462 35,746 $31,274 36,027 37,089 $22,117 41,412 $31,330 $31,329 33,184 35,301 $32,843 $38,177 $40,969 $40,993 29,688 35,890 34,381 Tabla\(\PageIndex{4}\): Datos de Ingresos para Mujeres - Los ingresos de los varones en cada estado de Estados Unidos, incluyendo el Distrito de Columbia y Puerto Rico, se dan en Ejemplo\(\PageIndex{3}\), y el ingreso de las mujeres se da en Ejemplo\(\PageIndex{4}\) (“Ingresos medios de,” 2013). Calcular un intervalo de confianza del 99% para la diferencia de ingresos entre hombres y mujeres en Estados Unidos.
- Se realizó un estudio que midió el volumen cerebral total (TBV) (in\(m m^{3}\)) de pacientes que tenían esquizofrenia y pacientes que se consideran normales. Ejemplo\(\PageIndex{5}\) contiene el TBV de los pacientes normales y Ejemplo\(\PageIndex{6}\) contiene el TBV de pacientes con esquizofrenia (“datos SOCR oct2009,” 2013). ¿Existe evidencia suficiente para demostrar que los pacientes con esquizofrenia tienen menos TBV en promedio que un paciente que se considera normal? Prueba al nivel del 10%.
1663407 1583940 1299470 1535137 1431890 1578698 1453510 1650348 1288971 1366346 1326402 1503005 1474790 1317156 1441045 1463498 1650207 1523045 1441636 1432033 1420416 1480171 1360810 1410213 1574808 1502702 1203344 1319737 1688990 1292641 1512571 1635918 Cuadro\(\PageIndex{5}\): Volumen Cerebral Total (in\(\mathrm{mm}^{3}\)) de Pacientes Normales 1331777 1487886 1066075 1297327 1499983 1861991 1368378 1476891 1443775 1337827 1658258 1588132 1690182 1569413 1177002 1387893 1483763 1688950 1563593 1317885 1420249 1363859 1238979 1286638 1325525 1588573 1476254 1648209 1354054 1354649 1636119 Tabla\(\PageIndex{6}\): Volumen cerebral total (in\(\mathrm{mm}^{3}\)) de pacientes con esquizofrenia - Se realizó un estudio que midió el volumen cerebral total (TBV) (in\(m m^{3}\)) de pacientes que tenían esquizofrenia y pacientes que se consideran normales. Ejemplo\(\PageIndex{5}\) contiene el TBV de los pacientes normales y Ejemplo\(\PageIndex{6}\) contiene el TBV de pacientes con esquizofrenia (“datos SOCR oct2009,” 2013). Calcular un intervalo de confianza del 90% para la diferencia en TBV de pacientes normales y pacientes con Esquizofrenia.
- La longitud de los ríos de Nueva Zelanda (NZ) que viajan al Océano Pacífico se dan en Ejemplo\(\PageIndex{7}\) y las longitudes de los ríos de Nueva Zelanda que viajan al Mar de Tasmania se dan en Ejemplo\(\PageIndex{8}\) (“Longitud de NZ,” 2013). ¿Los datos proporcionan evidencia suficiente para mostrar en promedio que los ríos que viajan al Océano Pacífico son más largos que los ríos que viajan al Mar de Tasmania? Utilizar un nivel de significancia del 5%.
209 48 169 138 64 97 161 95 145 90 121 80 56 64 209 64 72 288 322 Tabla\(\PageIndex{7}\): Longitudes (en km) de ríos NZ que desembocan en el Océano Pacífico 76 64 68 64 37 32 32 51 56 40 64 56 80 121 177 56 80 35 72 72 108 48 Tabla\(\PageIndex{8}\): Longitudes (en km) de ríos NZ que desembocan en el mar de Tasmania - La longitud de los ríos de Nueva Zelanda (NZ) que viajan al Océano Pacífico se dan en Ejemplo\(\PageIndex{7}\) y las longitudes de los ríos de Nueva Zelanda que viajan al Mar de Tasmania se dan en Ejemplo\(\PageIndex{8}\) (“Longitud de NZ,” 2013). Estimar la diferencia en la longitud media de los ríos entre los ríos en NZ que viajan al Océano Pacífico y los que viajan al Mar de Tasmania. Usa un nivel de confianza del 95%.
- El número de celulares por cada 100 residentes en países de Europa se da en Ejemplo\(\PageIndex{9}\) para el año 2010. El número de celulares por cada 100 residentes en países de las Américas se da en Ejemplo\(\PageIndex{10}\) también para el año 2010 (“Oficina de referencia de población”, 2013). ¿Hay pruebas suficientes para demostrar que el número medio de celulares en los países de Europa es mayor que en los países de las Américas? Prueba al nivel 1%.
100 76 100 130 75 84 112 84 138 133 118 134 126 188 129 93 64 128 124 122 109 121 127 152 96 63 99 95 151 147 123 95 67 67 118 125 110 115 140 115 141 77 98 102 102 112 118 118 54 23 121 126 47 Tabla\(\PageIndex{9}\): Número de teléfonos celulares por cada 100 residentes en Europa 158 117 106 159 53 50 78 66 88 92 42 3 150 72 86 113 50 58 70 109 37 32 85 101 75 69 55 115 95 73 86 157 100 119 81 113 87 105 96 Tabla\(\PageIndex{10}\): Número de teléfonos celulares por cada 100 residentes en América - El número de celulares por cada 100 residentes en países de Europa se da en Ejemplo\(\PageIndex{9}\) para el año 2010. El número de celulares por cada 100 residentes en países de las Américas se da en Ejemplo\(\PageIndex{10}\) también para el año 2010 (“Oficina de referencia de población”, 2013). Encuentre el intervalo de confianza del 98% para la diferencia en el número medio de celulares por cada 100 residentes en Europa y América.
- Una vacuna de vitamina K se administra a los bebés poco después del nacimiento. Las enfermeras de Northbay Healthcare participaron en un estudio para ver si la forma en que manejan a los bebés podría reducir el dolor que sienten los bebés (“SOCR data nips”, 2013). Una de las medidas tomadas fue cuánto tiempo, en segundos, lloró el infante tras recibir la vacuna. Se tomó una muestra aleatoria del grupo al que se le dio la toma mediante métodos convencionales (Ejemplo\(\PageIndex{11}\)), y se tomó una muestra aleatoria del grupo al que se le dio la toma donde la madre sujetó al lactante antes y durante la toma (Ejemplo\(\PageIndex{12}\)). ¿Hay evidencia suficiente para demostrar que los infantes lloraron menos en promedio cuando son retenidos por sus madres que si se los mantiene usando métodos convencionales? Prueba al nivel del 5%.
63 0 2 46 33 33 29 23 11 12 48 15 33 14 51 37 24 70 63 0 73 39 54 52 39 34 30 55 58 18 Tabla\(\PageIndex{11}\): Tiempo de llanto de los bebés a los que se les administró inyecciones 0 32 20 23 14 19 60 59 64 64 72 50 44 14 10 58 19 41 17 5 36 73 19 46 9 43 73 27 25 18 Tabla\(\PageIndex{12}\): Tiempo de llanto de los lactantes a los que se les administró inyecciones - Una vacuna de vitamina K se administra a los bebés poco después del nacimiento. Las enfermeras de Northbay Healthcare participaron en un estudio para ver si la forma en que manejan a los bebés podría reducir el dolor que sienten los bebés (“SOCR data nips”, 2013). Una de las medidas tomadas fue cuánto tiempo, en segundos, lloró el infante tras recibir la vacuna. Se tomó una muestra aleatoria del grupo al que se le dio la toma mediante métodos convencionales (Ejemplo\(\PageIndex{11}\)), y se tomó una muestra aleatoria del grupo al que se le dio la toma donde la madre sujetó al lactante antes y durante la toma (Ejemplo\(\PageIndex{12}\)). Calcular un intervalo de confianza de 95% para la diferencia media en el tiempo medio de llanto después de recibir una dosis de vitamina K entre los bebés mantenidos por métodos convencionales y los lactantes mantenidos por sus madres.
- Rehacer el problema 1 probando para el supuesto de varianzas iguales y luego usar la fórmula que utiliza la suposición de varianzas iguales (siga el procedimiento en Ejemplo\(\PageIndex{3}\)).
- Rehacer problema 2 probando para el supuesto de varianzas iguales y luego usar la fórmula que utiliza la suposición de varianzas iguales (siga el procedimiento en Ejemplo\(\PageIndex{3}\)).
- Rehacer problema 7 probando para el supuesto de varianzas iguales y luego usar la fórmula que utiliza la suposición de varianzas iguales (siga el procedimiento en Ejemplo\(\PageIndex{3}\)).
- Rehacer problema 8 probando para el supuesto de varianzas iguales y luego usar la fórmula que utiliza la suposición de varianzas iguales (siga el procedimiento en Ejemplo\(\PageIndex{3}\)).
- Rehacer problema 9 probando para el supuesto de varianzas iguales y luego usar la fórmula que utiliza la suposición de varianzas iguales (siga el procedimiento en Ejemplo\(\PageIndex{3}\)).
- Rehacer problema 10 probando para el supuesto de varianzas iguales y luego usar la fórmula que utiliza la suposición de varianzas iguales (siga el procedimiento en Ejemplo\(\PageIndex{3}\)).
- Contestar
-
Para todas las pruebas de hipótesis, solo se da la conclusión. Para todos los intervalos de confianza, solo se da el intervalo usando la tecnología. Ver solución para toda la respuesta.
- Rechazar Ho
- \(\$ 65443.80<\mu_{1}-\mu_{2}<\$ 13340.80\)
- No rechazar a Ho
- \(-51564.6 \mathrm{mm}^{3}<\mu_{1}-\mu_{2}<75656.6 \mathrm{mm}^{3}\)
- Rechazar Ho
- \(23.2818 \mathrm{km}<\mu_{1}-\mu_{2}<103.67 \mathrm{km}\)
- Rechazar Ho
- \(4.3641<\mu_{1}-\mu_{2}<37.5276\)
- No rechazar a Ho
- \(-10.9726 \mathrm{s}<\mu_{1}-\mu_{2}<11.3059 \mathrm{s}\)
- Rechazar Ho
- \(\$ 6544.98<\mu_{1}-\mu_{2}<\$ 13339.60\)
- Rechazar Ho
- \(4.8267<\mu_{1}-\mu_{2}<37.0649\)
- No rechazar a Ho
- \(-10.9713 \mathrm{s}<\mu_{1}-\mu_{2}<11.3047 \mathrm{s}\)


