10.1: Regresión
- Page ID
- 149841
Al comparar dos variables diferentes, me vienen a la mente dos preguntas: “¿Existe una relación entre dos variables?” y “¿Qué tan fuerte es esa relación?” Estas preguntas pueden ser respondidas mediante regresión y correlación. La regresión responde si existe una relación (nuevamente este libro explorará solo lineal) y la correlación responde qué tan fuerte es la relación lineal. Para introducir ambos conceptos, es más fácil mirar un conjunto de datos.
Ejemplo\(\PageIndex{1}\) if there is a relationship
¿Existe una relación entre el contenido de alcohol y la cantidad de calorías en la cerveza de 12 onzas? Para determinar si hay una se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza (“Calorías en la cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{1}\).
| Marca | Cervecería | Contenido de Alcohol | Calorías en 12 oz |
|---|---|---|---|
| Big Sky Scape Cabra Pale Ale | Elaboración de cerveza Big Sky | 4.70% | 163 |
| Sierra Nevada Cosecha Ale | Sierra Nevada | 6.70% | 215 |
| Reserva de Acero | MillerCoors | 8.10% | 222 |
| O'Doul's | Anheuser Busch | 0.40% | 70 |
| Luz de Coors | MillerCoors | 4.15% | 104 |
| Genesee Crema Ale | Elaboración de High Falls | 5.10% | 162 |
| Cerveza Sierra Nevada Summerfest | Sierra Nevada | 5.00% | 158 |
| Cerveza Michelob | Anheuser Busch | 5.00% | 155 |
| Perro Volador Estilo Perrito | Cervecería Flying Dog | 4.70% | 158 |
| Big Sky I.P.A. | Elaboración de cerveza Big Sky | 6.20% | 195 |
Solución
Para ayudar a determinar si hay una relación, ayuda a dibujar un diagrama de dispersión de los datos. Es útil establecer las variables aleatorias, y dado que en una clase de álgebra las variables se representan como x e y, esas etiquetas se usarán aquí. Ayuda a indicar qué variable es x y cuál es y.
Estado de variables aleatorias
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas
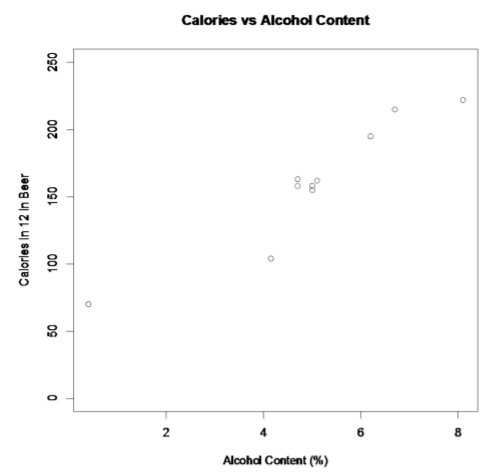.png)
Esta gráfica de dispersión se ve bastante lineal. No obstante, observe que hay una cerveza en la lista que en realidad se considera una cerveza sin alcohol. Ese valor es probablemente un valor atípico ya que es una cerveza sin alcohol. El resto del análisis no incluirá O'Doul's No se puede simplemente eliminar puntos de datos, sino que en este caso tiene más sentido, ya que todas las demás cervezas tienen un contenido de alcohol bastante grande.
Para encontrar la ecuación para la relación lineal, se utiliza el proceso de regresión para encontrar la línea que mejor se ajuste a los datos (a veces llamada la línea de mejor ajuste). El proceso consiste en trazar la línea a través de los datos y luego encontrar las distancias de un punto a la línea, que se denominan los residuos. La línea de regresión es la línea que hace que el cuadrado de los residuos sea lo más pequeño posible, por lo que a la línea de regresión también se le llama a veces la línea de mínimos cuadrados. La línea de regresión y los residuos se muestran en la Figura\(\PageIndex{2}\).
.png)
Para encontrar la ecuación de regresión (también conocida como línea de mejor ajuste o línea de mínimos cuadrados)
Dada una colección de datos de muestra pareados, la ecuación de regresión es
\(\hat{y}=a+b x\)
donde la pendiente =\(b=\dfrac{S S_{\mathrm{xy}}}{S S_{x}}\) e y -intercept =\(a=\overline{y}-b \overline{x}\)
Definición\(\PageIndex{1}\)
Los residuales son la diferencia entre los valores reales y los valores estimados.
residual\(=y-\hat{y}\)
Definición\(\PageIndex{2}\)
SS significa suma de cuadrados. Entonces estás resumiendo cuadrados. Con el subíndice xy, en realidad no estás sumando cuadrados, pero puedes pensarlo de esa manera en un sentido extraño.
\(\begin{array}{l}{S S_{x y}=\sum(x-\overline{x})(y-\overline{y})} \\ {S S_{x}=\sum(x-\overline{x})^{2}} \\ {S S_{y}=\sum(y-\overline{y})^{2}}\end{array}\)
Nota
La forma más fácil de encontrar la ecuación de regresión es usar la tecnología.
La variable independiente, también llamada variable explicativa o variable predictora, es el valor x en la ecuación. La variable independiente es la que se utiliza para predecir cuál es la otra variable. La variable dependiente depende del valor independiente que elija. También responde a la variable explicativa y a veces se le llama la variable respuesta. En el ejemplo de contenido de alcohol y calorías, tiene un poco más de sentido decir que usarías el contenido de alcohol en una cerveza para predecir el número de calorías en la cerveza.
Definición\(\PageIndex{3}\)
La ecuación poblacional se ve así:
\(\begin{array}{l}{y=\beta_{o}+\beta_{1} x} \\ {\beta_{o}=\text { slope }} \\ {\beta_{1}=y \text { -intercept }}\end{array}\)
\(\hat{y}\)se utiliza para predecir y.
Supuestos de la línea de regresión:
- El conjunto\((x, y)\) de pares ordenados es una muestra aleatoria de la población de todos estos\((x, y)\) pares posibles.
- Por cada valor fijo de x, los valores y tienen una distribución normal. Todas las distribuciones y tienen la misma varianza, y para un valor x dado, la distribución de valores y tiene una media que se encuentra en la línea de mínimos cuadrados. También asumes que para una y fija, cada x tiene su propia distribución normal. Esto es difícil de entender, por lo que puedes usar lo siguiente para determinar si tienes una distribución normal.
- Mire para ver si la gráfica de dispersión tiene un patrón lineal.
- Examine los residuos para ver si hay aleatoriedad en los residuales. Si hay un patrón a los residuales, entonces hay un problema en los datos.
Ejemplo\(\PageIndex{2}\) find the equation of the regression line
- ¿Existe una relación positiva entre el contenido de alcohol y el número de calorías en la cerveza de 12 onzas? Para determinar si existe una relación lineal positiva, se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza para varias cervezas diferentes (“Calorías en la cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{2}\).
- Usa la ecuación de regresión para encontrar el número de calorías cuando el contenido de alcohol es de 6.50%.
- Usa la ecuación de regresión para encontrar el número de calorías cuando el contenido de alcohol es de 2.00%.
- Encuentre los residuos y luego grafique los residuos frente a los valores x.
| Marca | Cervecería | Contenido de Alcohol | Calorías en 12 oz |
|---|---|---|---|
| Big Sky Scape Cabra Pale Ale | Elaboración de cerveza Big Sky | 4.70% | 163 |
| Sierra Nevada Cosecha Ale | Sierra Nevada | 6.70% | 215 |
| Reserva de Acero | MillerCoors | 8.10% | 222 |
| O'Doul's | Anheuser Busch | 0.40% | 70 |
| Luz de Coors | MillerCoors | 4.15% | 104 |
| Genesee Crema Ale | Elaboración de High Falls | 5.10% | 162 |
| Cerveza Sierra Nevada Summerfest | Sierra Nevada | 5.00% | 158 |
| Cerveza Michelob | Anheuser Busch | 5.00% | 155 |
| Perro Volador Estilo Perrito | Cervecería Flying Dog | 4.70% | 158 |
| Big Sky I.P.A. | Elaboración de cerveza Big Sky | 6.20% | 195 |
Solución
a. Estado de variables aleatorias
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas
Comprobación de suposiciones:
- Se tomó una muestra aleatoria como se indica en el problema.
- La distribución para cada valor calórico se distribuye normalmente por cada valor del contenido de alcohol en la cerveza.
- De Ejemplo\(\PageIndex{1}\), la gráfica de dispersión se ve bastante lineal.
- La gráfica residual versus la gráfica de valores x parece bastante aleatoria. (Ver Figura\(\PageIndex{5}\).)
Parece que la distribución de calorías es una distribución normal.
Para encontrar la ecuación de regresión en la calculadora TI-83/84, ponga las x en L1 y las y en L2. Después vaya a STAT, a PRUEBAS, y elija LineGTEST. La configuración está en la Figura\(\PageIndex{3}\). La razón por la que se eligió >0 es porque se hizo la pregunta si hubo una relación positiva. Si te preguntan si hay una relación negativa, entonces elige <0. Si solo te preguntan si hay una relación, entonces elige\(\neq 0\). En este momento la elección no hará otra cosa, pero será importante más adelante.
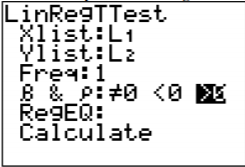.png)
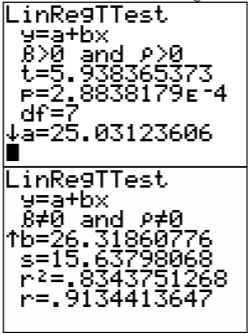.png)
De esto se puede ver que
\(\hat{y}=25.0+26.3 x\)
Para encontrar la ecuación de regresión usando R, el comando es lm (variable dependiente ~ variable independiente), donde ~ es el símbolo de tilde ubicado en la parte superior izquierda de la mayoría de los teclados. Entonces para este ejemplo, el comando sería lm (calorías ~ alcohol), y la salida sería
Llamar:
lm (fórmula = calorías ~ alcohol)
Coeficientes:
(Interceptar) alcohol
25.03 26.32
De esto se puede ver que la intersección y es 25.03 y la pendiente es 26.32. Entonces la ecuación de regresión es\(\hat{y}=25.0+26.3 x\).
Recuerde, esta es una estimación para la regresión verdadera. Una muestra aleatoria diferente produciría una estimación diferente.
b.\(\begin{array}{l}{x_{o}=6.50} \\ {\hat{y}=25.0+26.3(6.50)=196 \text { calories }}\end{array}\)
Si estás tomando una cerveza que tiene un 6.50% de contenido alcohólico, entonces probablemente esté cerca de 196 calorías. Observe, el número medio de calorías es de 170 calorías. Este valor de 196 parece una mejor estimación que la media al mirar los datos originales. La ecuación de regresión es una mejor estimación que solo la media.
c.\(\begin{array}{l}{x_{o}=2.00} \\ {\hat{y}=25.0+26.3(2.00)=78 \text { calories }}\end{array}\)
Si estás tomando una cerveza que tiene un 2.00% de contenido alcohólico, entonces probablemente tenga cerca de 78 calorías. Esto no parece una muy buena estimación. Esta estimación es lo que se denomina extrapolación. No es buena idea predecir valores que están muy fuera del rango de los datos originales. Esto se debe a que nunca se puede estar seguro de que la ecuación de regresión es válida para datos fuera de los datos originales.
d. Para encontrar los residuos, busque\(\hat{y}\) por cada valor x. Luego resta cada uno\(\hat{y}\) del valor y dado para encontrar los residuales. Darse cuenta de que estos son residuos de muestra ya que se calculan a partir de valores de muestra. Lo mejor es hacerlo en una hoja de cálculo.
| x | y | \(\hat{y}=25.0+26.3 x\) | \(y-\hat{y}\) |
| 4.70 | 163 | 148.61 | 14.390 |
| 6.70 | 215 | 201.21 | 13.790 |
| 8.10 | 222 | 238.03 | -16.030 |
| 4.15 | 104 | 134.145 | -30.145 |
| 5.10 | 162 | 159.13 | 2.870 |
| 5.00 | 158 | 156.5 | 1.500 |
| 5.00 | 155 | 156.5 | -1.500 |
| 4.70 | 158 | 148.61 | 9.390 |
| 6.20 | 195 | 188.06 | 6.940 |
Observe que los residuos se suman hasta cerca de 0. No suman exactamente 0 en este ejemplo debido al error de redondeo. Normalmente los residuos suman 0.
Puedes usar R para obtener los residuos. El comando es
lm.out = lm (variable dependiente ~ variable independiente) — esto define el modelo lineal con un nombre para que pueda usarlo más adelante.
Luego residual (lm.out) — produce los residuales.
Para este ejemplo, el comando sería
lm (calorías~alcohol)
Llamar:
lm (fórmula = calorías ~ alcohol)
Coeficientes:
(Interceptar) alcohol
25.03 26.32
> residuos (lm.out)
\(\begin{array}{ccccc}{1} & {2} & {3} & {4} & {5} & {6} & {7} & {8} & {9} \\ {14.271307} & {13.634092} & {-16.211959} & {-30.253458} & {2.743864} & {1.375725} & {-1.624275} & {9.271307} & {6.793396}\end{array}\)
Entonces el primer residual es 14.271307 y pertenece al primer valor x. El residual 13.634092 pertenece al segundo valor x, y así sucesivamente.
A continuación, puede graficar los residuos frente a la variable independiente usando el comando plot. Para este ejemplo, el comando sería plot (alcohol, residuales (lm.out), main="residuales para calorías de cerveza versus contenido de alcohol”, xlab="Contenido de alcohol”, ylab="residuos”). A veces es útil ver el eje x en la gráfica, así que después de crear la gráfica, escriba el comando abline (0,0).
La gráfica de los residuos frente a los valores x se encuentra en la Figura\(\PageIndex{5}\). Parecen ser algo aleatorias.
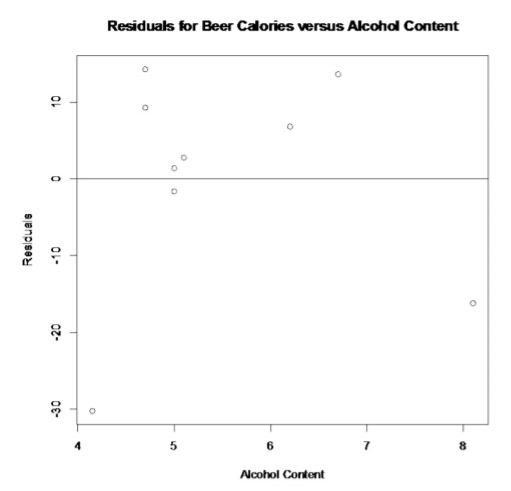.png)
Observe, que el valor de 6.50% cae dentro del rango de los valores x originales. Los procesos de predicción de valores usando una x dentro del rango de valores x originales se llama interpolación. El valor de 2.00% está fuera del rango de valores x originales. El uso de un valor x que está fuera del rango de los valores x originales se llama extrapolación. Al predecir valores usando interpolación, normalmente puedes sentirte bastante seguro de que ese valor estará cerca del valor verdadero. Cuando extrapolas, no estás realmente seguro de que el valor predicho esté cerca del valor verdadero. Esto es porque cuando interpolas, conoces la ecuación que predice, pero cuando extrapolas, no estás realmente seguro de que tu relación siga siendo válida. De hecho, la relación podría cambiar para diferentes valores x.
Un ejemplo de esto es cuando usas regresión para llegar a una ecuación para predecir el crecimiento de una ciudad, como Flagstaff, AZ. Con base en el análisis se determinó que la población de Flagstaff estaría muy por encima de 50 mil para 1995. No obstante, cuando se realizó un censo en 1995, la población era inferior a 50 mil. Esto se debe a que extrapolaron y el factor de crecimiento que estaban usando obviamente había cambiado desde principios de la década de 1990. Los factores de crecimiento pueden cambiar por muchas razones, como el crecimiento del empleo, el estancamiento del empleo, la enfermedad, los artículos que dicen un gran lugar para vivir, etc. date cuenta de que cuando extrapolas, tu predicho el valor puede no estar cerca del valor real que observa.
¿Qué significa la pendiente en el contexto de este problema?
\(m=\dfrac{\Delta y}{\Delta x}=\dfrac{\Delta \text { calories }}{\Delta \text { alcohol content }}=\dfrac{26.3 \text { calories }}{1 \%}\)
Las calorías aumentan 26.3 calorías por cada incremento de 1% en el contenido de alcohol.
La intercepción y en muchos casos carece de sentido. En este caso, significa que si una bebida tiene 0 contenido de alcohol, entonces tendría 25.0 calorías. Esto puede ser razonable, pero recuerde que este valor es una extrapolación por lo que puede estar equivocado.
Consideremos de nuevo los residuos. Según los datos, una cerveza con 6.7% de alcohol tiene 215 calorías. El valor previsto es de 201 calorías.
Residual = real - predicho
=215 - 201
=14
Esta desviación significa que el valor real estaba 14 por encima del valor predicho. Eso no está tan lejos. Algunos de los valores reales difieren en gran medida del valor predicho. Esto se debe a la variabilidad en la variable dependiente. Cuanto mayores sean los residuos, menos el modelo explica la variabilidad en la variable dependiente. Se necesita una manera de calcular qué tan bien explica el modelo la variabilidad en la variable dependiente. Esto se explorará en la siguiente sección.
El siguiente ejemplo demuestra el proceso a seguir al usar las fórmulas para encontrar la ecuación de regresión, aunque es mejor usar la tecnología. Esto se debe a que si el modelo lineal no se ajusta bien a los datos, entonces podrías probar algunos de los otros modelos que están disponibles a través de la tecnología.
Ejemplo\(\PageIndex{3}\) calculating the regression equation with the formula
¿Existe una relación entre el contenido de alcohol y la cantidad de calorías en la cerveza de 12 onzas? Para determinar si hay una se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza (“Calorías en la cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{2}\). Encuentra la ecuación de regresión a partir de la fórmula.
Solución
Estado de variables aleatorias
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas
| Contenido de Alcohol | Calorías | \(x-\overline{x}\) | \(y-\overline{y}\) | \((x-\overline{x})^{2}\) | \((y-\overline{y})^{2}\) | \((x-\overline{x})(y-\overline{y})\) |
|---|---|---|---|---|---|---|
| 4.70 | 163 | \ (x-\ overline {x}\) ">-0.8167 | \ (y-\ overline {y}\) ">-7.2222 | \ ((x-\ overline {x}) ^ {2}\) ">0.6669 | \ ((y-\ overline {y}) ^ {2}\) ">52.1065 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">5.8981 |
| 6.70 | 215 | \ (x-\ overline {x}\) ">1.1833 | \ (y-\ overline {y}\) ">44.7778 | \ ((x-\ overline {x}) ^ {2}\) ">1.4003 | \ ((y-\ overline {y}) ^ {2}\) ">2005.0494 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">52.9870 |
| 8.10 | 222 | \ (x-\ overline {x}\) ">2.5833 | \ (y-\ overline {y}\) ">51.7778 | \ ((x-\ overline {x}) ^ {2}\) ">6.6736 | \ ((y-\ overline {y}) ^ {2}\) ">2680.9383 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">133.7595 |
| 4.15 | 104 | \ (x-\ overline {x}\) ">-1.3667 | \ (y-\ overline {y}\) ">-66.2222 | \ ((x-\ overline {x}) ^ {2}\) ">1.8678 | \ ((y-\ overline {y}) ^ {2}\) ">4385.3827 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">90.5037 |
| 5.10 | 162 | \ (x-\ overline {x}\) ">-0.4167 | \ (y-\ overline {y}\) ">-8.2222 | \ ((x-\ overline {x}) ^ {2}\) ">0.1736 | \ ((y-\ overline {y}) ^ {2}\) ">67.6049 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">3.4259 |
| 5.00 | 158 | \ (x-\ overline {x}\) ">-0.5167 | \ (y-\ overline {y}\) ">-12.2222 | \ ((x-\ overline {x}) ^ {2}\) ">0.2669 | \ ((y-\ overline {y}) ^ {2}\) ">149.3827 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">6.3148 |
| 5.00 | 155 | \ (x-\ overline {x}\) ">-0.5167 | \ (y-\ overline {y}\) ">-15.2222 | \ ((x-\ overline {x}) ^ {2}\) ">0.2669 | \ ((y-\ overline {y}) ^ {2}\) ">231.7160 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">7.8648 |
| 4.70 | 158 | \ (x-\ overline {x}\) ">-0.8167 | \ (y-\ overline {y}\) ">-12.2222 | \ ((x-\ overline {x}) ^ {2}\) ">0.6669 | \ ((y-\ overline {y}) ^ {2}\) ">149.3827 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">9.9815 |
| 6.20 | 195 | \ (x-\ overline {x}\) ">0.6833 | \ (y-\ overline {y}\) ">24.7778 | \ ((x-\ overline {x}) ^ {2}\) ">0.4669 | \ ((y-\ overline {y}) ^ {2}\) ">613.9383 | \ ((x-\ overline {x}) (y-\ overline {y})\) ">16.9315 |
| 5.516667 =\(\overline{x}\) | 170.2222 =\(\overline{y}\) | \ (x-\ overline {x}\) "> | \ (y-\ overline {y}\) "> | \ ((x-\ overline {x}) ^ {2}\) ">12.45 =\(S S_{x}\) | \ ((y-\ overline {y}) ^ {2}\) ">10335.5556 =\(S S_{y}\) | \ ((x-\ overline {x}) (y-\ overline {y})\) ">327.6667 =\(S S_{xy}\) |
pendiente:\(b=\dfrac{S S_{x y}}{S S_{x}}=\dfrac{327.6667}{12.45} \approx 26.3\)
y -interceptar:\(a=\overline{y}-b \overline{x}=170.222-26.3(5.516667) \approx 25.0\)
Ecuación de regresión:\(\hat{y}=25.0+26.3 x\)
Tarea
Ejercicio\(\PageIndex{1}\)
Para cada problema, indique las variables aleatorias. Además, mira para ver si hay algún valor atípico que necesite ser eliminado. Hacer el análisis de regresión con y sin los puntos atípicos sospechosos para determinar si su eliminación afecta la regresión. Los conjuntos de datos de esta sección se utilizan en la tarea para las secciones 10.2 y 10.3 también.
- Cuando un antropólogo encuentra restos esqueléticos, necesita averiguar la altura de la persona. Se recolectaron la altura de una persona (en cm) y la longitud de su hueso metacarpiano 1 (en cm) y se encuentran en Ejemplo\(\PageIndex{5}\) (“Predicción de altura”, 2013). Crear un diagrama de dispersión y encontrar una ecuación de regresión entre la altura de una persona y la longitud de su metacarpiano. Luego usa la ecuación de regresión para encontrar la altura de una persona para una longitud metacarpiana de 44 cm y para una longitud metacarpiana de 55 cm. ¿Qué altura que calculaste crees que está más cerca de la verdadera altura de la persona? ¿Por qué?
Largo del Metacarpiano (cm) Altura de la persona (cm) 45 171 51 178 39 157 41 163 48 172 49 183 46 173 43 175 47 173 Tabla\(\PageIndex{5}\): Datos de Metacarpiano versus Altura - Ejemplo\(\PageIndex{6}\) contiene el valor de la casa y la cantidad de ingresos por alquiler en un año que la casa aporta (“Capital y renta”, 2013). Cree un diagrama de dispersión y encuentre una ecuación de regresión entre el valor de la casa y los ingresos por alquiler. Luego usa la ecuación de regresión para encontrar los ingresos de renta de una casa por valor de 230,000 dólares y para una casa por un valor de $400,000. ¿Qué ingresos por alquiler que calculaste crees que está más cerca de los verdaderos ingresos por alquiler? ¿Por qué?
Valor Renta Valor Renta Valor Renta Valor Renta 81000 6656 77000 4576 75000 7280 67500 6864 95000 7904 94000 8736 90000 6240 85000 7072 121000 12064 115000 7904 110000 7072 104000 7904 135000 8320 130000 9776 126000 6240 125000 7904 145000 8320 140000 9568 140000 9152 135000 7488 165000 13312 165000 8528 155000 7488 148000 8320 178000 11856 174000 10400 170000 9568 170000 12688 200000 12272 200000 10608 194000 11232 190000 8320 214000 8528 208000 10400 200000 10400 200000 8320 240000 10192 240000 12064 240000 11648 225000 12480 289000 11648 270000 12896 262000 10192 244500 11232 325000 12480 310000 12480 303000 12272 300000 12480 Tabla\(\PageIndex{6}\): Datos del Valor de la Casa versus Renta - El Banco Mundial recopila información sobre la esperanza de vida de una persona en cada país (“Esperanza de vida en,” 2013) y la tasa de fecundidad por mujer en el país (“Tasa de fertilidad”, 2013). Los datos de 24 países seleccionados al azar para el año 2011 se encuentran en Ejemplo\(\PageIndex{7}\). Crear un diagrama de dispersión de los datos y encontrar una ecuación de regresión lineal entre la tasa de fertilidad y la esperanza de vida. A continuación, utilice la ecuación de regresión para encontrar la esperanza de vida para un país que tenga una tasa de fecundidad de 2.7 y para un país con tasa de fecundidad de 8.1. ¿Cuál esperanza de vida que calculaste crees que está más cerca de la verdadera esperanza de vida? ¿Por qué?
Tasa de Fertilidad Esperanza de vida 1.7 77.2 5.8 55.4 2.2 69.9 2.1 76.4 1.8 75.0 2.0 78.2 2.6 73.0 2.8 70.8 1.4 82.6 2.6 68.9 1.5 81.0 6.9 54.2 2.4 67.1 1.5 73.3 2.5 74.2 1.4 80.7 2.9 72.1 2.1 78.3 4.7 62.9 6.8 54.4 5.2 55.9 4.2 66.0 1.5 76.0 3.9 72.3 Tabla\(\PageIndex{7}\): Datos de tasas de fecundidad versus esperanza de vida - El Banco Mundial recopiló datos sobre el porcentaje del PIB que un país gasta en gastos de salud (“Gasto de salud”, 2013) y también el porcentaje de mujeres que reciben atención prenatal (“Mujer embarazada que recibe”, 2013). Los datos de los países donde se dispone de esta información para el año 2011 se encuentran en Ejemplo\(\PageIndex{8}\). Crear un diagrama de dispersión de los datos y encontrar una ecuación de regresión entre el porcentaje gastado en el gasto en salud y el porcentaje de mujeres que reciben atención prenatal. Entonces usa la ecuación de regresión para encontrar el porcentaje de mujeres que reciben atención prenatal para un país que gasta 5.0% del PIB en gastos de salud y para un país que gasta 12.0% del PIB. ¿Qué porcentaje de atención prenatal que calculaste crees que está más cerca del porcentaje verdadero? ¿Por qué?
Gasto en Salud (% del PIB) Atención Prenatal (%) 9.6 47.9 3.7 54.6 5.2 93.7 5.2 84.7 10.0 100.0 4.7 42.5 4.8 96.4 6.0 77.1 5.4 58.3 4.8 95.4 4.1 78.0 6.0 93.3 9.5 93.3 6.8 93.7 6.1 89.8 Tabla\(\PageIndex{8}\): Datos de Gasto en Salud versus Atención Prenatal - La altura y el peso de los beisbolistas están en Ejemplo\(\PageIndex{9}\) (“MLB heightsweights,” 2013). Crear un diagrama de dispersión y encontrar una ecuación de regresión entre la altura y el peso de los jugadores de béisbol. Entonces usa la ecuación de regresión para encontrar el peso de un beisbolista que mide 75 pulgadas de alto y para un beisbolista que mide 68 pulgadas de alto. ¿Qué peso que calculaste crees que está más cerca del peso verdadero? ¿Por qué?
Altura (pulgadas) Peso (libras) 76 212 76 224 72 180 74 210 75 215 71 200 77 235 78 235 77 194 76 185 72 180 72 170 75 220 74 228 73 210 72 180 70 185 73 190 71 186 74 200 74 200 75 210 79 240 72 208 75 180 Tabla\(\PageIndex{9}\): Alturas y Pesos de Beisbolistas - Diferentes especies tienen diferentes pesos corporales y pesos cerebrales están en Ejemplo\(\PageIndex{10}\). (“Brain2BodyWeight”, 2013). Cree una gráfica de dispersión y encuentre una ecuación de regresión entre los pesos corporales y los pesos cerebrales. Luego usa la ecuación de regresión para encontrar el peso cerebral para una especie que tiene un peso corporal de 62 kg y para una especie que tiene un peso corporal de 180,000 kg. ¿Qué peso cerebral que calculaste crees que está más cerca del verdadero peso cerebral? ¿Por qué?
Especies Peso Corporal (kg) Peso Cerebral (kg) Humano Recién Nacido 3.20 0.37 Humano Adulto 73.00 1.35 Pithecanthropus Hombre 70.00 0.93 Ardilla 0.80 0.01 Hámster 0.15 0.00 Chimpancé 50.00 0.42 Conejo 1.40 0.01 Perro (Beagle) 10.00 0.07 Cat 4.50 0.03 Rata 0.40 0.00 Delfín de nariz de botella 400.00 1.50 Castor 24.00 0.04 Gorila 320.00 0.50 Tiger 170.00 0.26 Búho 1.50 0.00 Camel 550.00 0.76 Elefante 4600.00 6.00 León 187.00 0.24 Ovejas 120.00 0.14 Morsa 800.00 0.93 Caballo 450.00 0.50 Vaca 700.00 0.44 Jirafa 950.00 0.53 Lagarto Verde 0.20 0.00 Cachalote 35000.00 7.80 Tortuga 3.00 0.00 Cocodrilo 270.00 0.01 Tabla\(\PageIndex{10}\): Pesos corporales y pesos cerebrales de especies - Se tomó una muestra aleatoria de hotdogs de carne y se midió la cantidad de sodio (en mg) y calorías. (“Data hotdogs”, 2013) Los datos están en Ejemplo\(\PageIndex{11}\). Cree una gráfica de dispersión y encuentre una ecuación de regresión entre la cantidad de calorías y la cantidad de sodio. Luego usa la ecuación de regresión para encontrar la cantidad de sodio que tiene un hotdog de res si es de 170 calorías y si es de 120 calorías. ¿Qué nivel de sodio que calculaste crees que está más cerca del verdadero nivel de sodio? ¿Por qué?
Calorías Sodio 186 495 181 477 176 425 149 322 184 482 190 587 158 370 139 322 175 479 148 375 152 330 111 300 141 386 153 401 190 645 157 440 131 317 149 319 135 298 132 253 Tabla\(\PageIndex{11}\): Calorías y Niveles de Sodio en Hotdogs de Carne - El ingreso per cápita en 1960 dólares para los países europeos y el porcentaje de la fuerza laboral que trabaja en la agricultura en 1960 están en Ejemplo\(\PageIndex{12}\) (“Desarrollo económico de la OCDE”, 2013). Crear un diagrama de dispersión y encontrar una ecuación de regresión entre el porcentaje de la fuerza laboral en la agricultura y el ingreso per cápita. Entonces usa la ecuación de regresión para encontrar el ingreso per cápita en un país que tiene 21 por ciento de mano de obra en la agricultura y en un país que tiene 2 por ciento de mano de obra en la agricultura. ¿Cuál ingreso per cápita que calculaste crees que está más cerca del ingreso verdadero? ¿Por qué?
País Porcentaje en Agricultura Ingreso per cápita Suecia 14 1644 Suiza 11 1361 Luxemburgo 15 1242 U. Reino 4 1105 Dinamarca 18 1049 W. Alemania 15 1035 Francia 20 1013 Bélgica 6 1005 Noruega 20 977 Islandia 25 839 Países Bajos 11 810 Austria 23 681 Irlanda 36 529 Italia 27 504 Grecia 56 324 España 42 290 Portugal 44 238 Turquía 79 177 Tabla\(\PageIndex{12}\): Porcentaje de mano de obra en agricultura e ingreso per cápita para países europeos - El tabaquismo y el cáncer se han relacionado. El número de muertes por cien mil por cáncer de vejiga y el número de cigarrillos vendidos per cápita en 1960 se encuentran en Ejemplo\(\PageIndex{13}\) (“Fumar y cáncer”, 2013). Crear un diagrama de dispersión y encontrar una ecuación de regresión entre el tabaquismo y las muertes por cáncer de vejiga. Luego usa la ecuación de regresión para encontrar el número de muertes por cáncer de vejiga cuando las ventas de cigarrillos fueron de 20 per cápita y cuando las ventas de cigarrillos fueron de 6 per cápita. ¿Qué número de muertes que calculaste crees que está más cerca del número verdadero? ¿Por qué?
Venta de Cigarrillos (per cápita) Muertes por cáncer de vejiga (por cada 100 mil) Venta de Cigarrillos (per cápita) Muertes por cáncer de vejiga (por cada 100 mil) 18.20 2.90 42.40 6.54 25.82 3.52 28.64 5.98 18.24 2.99 21.16 2.90 28.60 4.46 29.14 5.30 31.10 5.11 19.96 2.89 33.60 4.78 26.38 4.47 40.46 5.60 23.44 2.93 28.27 4.46 23.78 4.89 20.10 3.08 29.18 4.99 27.91 4.75 18.06 3.25 26.18 4.09 20.94 3.64 22.12 4.23 20.08 2.94 21.84 2.91 22.57 3.21 23.44 2.86 14.00 3.31 21.58 4.65 25.89 4.63 28.92 4.79 21.17 4.04 25.91 5.21 21.25 5.14 26.92 4.69 22.86 4.78 24.96 5.27 28.04 3.20 22.06 3.72 30.34 3.46 16.08 3.06 23.75 3.95 27.56 4.04 23.32 3.72 Tabla\(\PageIndex{13}\): Número de cigarrillos y número de muertes por cáncer de vejiga en 1960 - El peso de un automóvil puede influir en el kilometraje que pueda obtener el automóvil. Se recolectó una muestra aleatoria de pesos y kilometraje de los autos y se encuentran en Ejemplo\(\PageIndex{14}\) (“Kilometraje de autos de pasajeros”, 2013). Crea un diagrama de dispersión y encuentra una ecuación de regresión entre el peso de los autos y el kilometraje. Después usa la ecuación de regresión para encontrar el kilometraje en un auto que pesa 3800 libras y en un auto que pesa 2000 libras. ¿Qué kilometraje que calculaste crees que está más cerca del kilometraje verdadero? ¿Por qué?
Peso (100 libras) Kilometraje (mpg) 22.5 53.3 22.5 41.1 22.5 38.9 25.0 40.9 27.5 46.9 27.5 36.3 30.0 32.2 30.0 32.2 30.0 31.5 30.0 31.4 30.0 31.4 35.0 32.6 35.0 31.3 35.0 31.3 35.0 28.0 35.0 28.0 35.0 28.0 40.0 23.6 40.0 23.6 40.0 23.4 40.0 23.1 45.0 19.5 45.0 17.2 45.0 17.0 55.0 13.2 Tabla\(\PageIndex{14}\): Pesos y Kilometraje de Autos
- Contestar
-
Para la regresión, sólo se da la ecuación. Ver soluciones para toda la respuesta.
1. \(\hat{y}=1.719 x+93.709\)
3. \(\hat{y}=-4.706 x+84.873\)
5. \(\hat{y}=5.859 x-230.942\)
7. \(\hat{y}=4.0133 x-228.3313\)
9. \(\hat{y}=0.12182 x+1.08608\)


