10.2: Correlación

Existe una correlación entre dos variables cuando los valores de una variable están asociados de alguna manera con los valores de la otra variable.

Cuando ves un patrón en los datos dices que hay una correlación en los datos. Aunque este libro solo trata de patrones lineales, los patrones pueden ser exponenciales, logarítmicos o periódicos. Para ver este patrón, se puede dibujar una gráfica de dispersión de los datos.

Recuerda leer gráficas de izquierda a derecha, igual que lees palabras. Si la gráfica sube la correlación es positiva y si la gráfica baja la correlación es negativa.

Se utilizan las palabras “débil”, “moderado” y “fuerte” para describir la fuerza de la relación entre las dos variables.

Cifras

El coeficiente de correlación lineal es un número que describe la fuerza de la relación lineal entre las dos variables. También se le llama el coeficiente de correlación de Pearson después de Karl Pearson quien lo desarrolló. El símbolo para el coeficiente de correlación lineal muestral es r. El símbolo para el coeficiente de correlación poblacional es\(\rho\) (letra griega rho).

La fórmula para r es

\(r=\dfrac{S S_{x y}}{\sqrt{S S_{x} S S_{y}}}\)

Dónde

\(\begin{array}{l}{S S_{x}=\sum(x-\overline{x})^{2}} \\ {S S_{y}=\sum(y-\overline{y})^{2}} \\ {S S_{x y}=\sum(x-\overline{x})(y-\overline{y})}\end{array}\)

Los supuestos de correlación lineal son los mismos que los supuestos para la línea de regresión:

1. El conjunto (x, y) de pares ordenados es una muestra aleatoria de la población de todos esos pares posibles (x, y).
2. Por cada valor fijo de x, los valores y tienen una distribución normal. Todas las distribuciones y tienen la misma varianza, y para un valor x dado, la distribución de valores y tiene una media que se encuentra en la línea de mínimos cuadrados. También asumes que para una y fija, cada x tiene su propia distribución normal. Esto es difícil de entender, por lo que puedes usar lo siguiente para determinar si tienes una distribución normal.
   1. Mire para ver si la gráfica de dispersión tiene un patrón lineal.
   2. Examine los residuos para ver si hay aleatoriedad en los residuales. Si hay un patrón a los residuales, entonces hay un problema en los datos.

Nota

Interpretación del coeficiente de correlación

r siempre está entre -1 y 1. r = -1 significa que hay una correlación lineal negativa perfecta y r = 1 significa que hay una correlación positiva perfecta. Cuanto más cerca está r a 1 o -1, más fuerte es la correlación. Cuanto más cerca r está a 0, más débil es la correlación.

CUIDADO: r = 0 no significa que no haya correlación. Simplemente significa que no hay correlación lineal. Podría haber un patrón curvo muy fuerte.

r

¿Qué tan fuerte es la relación positiva entre el contenido de alcohol y el número de calorías en la cerveza de 12 onzas? Para determinar si existe una correlación lineal positiva, se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza para varias cervezas diferentes (“Calorías en cerveza”, 2011), y los datos están en la Tabla\(\PageIndex{1}\). Encuentra el coeficiente de correlación e interpreta ese valor.

Tabla\(\PageIndex{1}\): Contenido Alcohólico y Calórico en Cerveza sin Valores Aatípicos

Marca	Cervecería	Contenido de Alcohol	Calorías en 12 oz
Big Sky Scape Cabra Pale Ale	Elaboración de cerveza Big Sky	4.70%	163
Sierra Nevada Cosecha Ale	Sierra Nevada	6.70%	215
Reserva de Acero	MillerCoors	8.10%	222
Luz de Coors	MillerCoors	4.15%	104
Genesee Crema Ale	Elaboración de High Falls	5.10%	162
Cerveza Sierra Nevada Summerfest	Sierra Nevada	5.00%	158
Cerveza Michelob	Anheuser Busch	5.00%	155
Perro Volador Estilo Perrito	Cervecería Flying Dog	4.70%	158
Big Sky I.P.A.	Elaboración de cerveza Big Sky	6.20%	195

Solución

Estado de variables aleatorias

x = contenido de alcohol en la cerveza

y = calorías en cerveza de 12 onzas

Comprobación de suposiciones:

De Ejemplo\(\PageIndex{2}\), se han cumplido los supuestos.

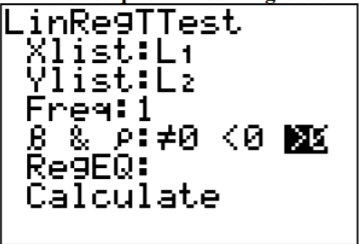
Para calcular el coeficiente de correlación usando la calculadora TI-83/84, utilice el LineRTEST en el menú STAT. La configuración está en la Figura\(\PageIndex{2}\). La razón por la que se eligió >0 es porque se hizo la pregunta si hubo una correlación positiva. Si se le pregunta si hay una correlación negativa, elija <0. Si solo te preguntan si hay una correlación, entonces elige\(\neq 0\). En este momento la elección no hará otra cosa, pero será importante más adelante.

Figura\(\PageIndex{2}\): Configuración para la Prueba de Regresión Lineal en TI-83/84

Figura\(\PageIndex{3}\): Resultados para la Prueba de Regresión Lineal en TI-83/84

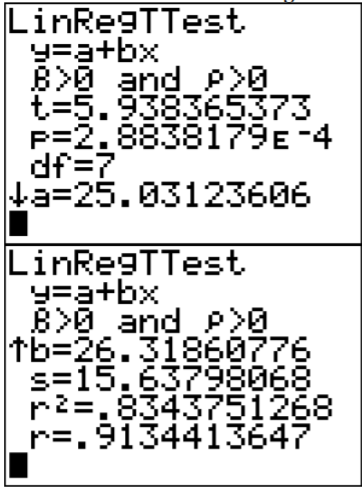
Para calcular el coeficiente de correlación en R, el comando es cor (variable independiente, variable dependiente). Entonces para este ejemplo el comando sería cor (alcohol, calorías). La salida es

[1] 0.9134414

El coeficiente de correlación es r = 0.913. Esto está cerca de 1, por lo que parece que hay una correlación fuerte y positiva.

Causalidad

Un error común que cometen las personas es asumir que debido a que existe una correlación, entonces una variable causa la otra. Por lo general, este no es el caso. Eso sería como decir que la cantidad de alcohol en la cerveza hace que tenga cierto número de calorías. Sin embargo, la fermentación de azúcares es lo que provoca el contenido de alcohol. Cuantos más azúcares tengas, más alcohol se puede hacer, y cuanto más azúcar, mayores son las calorías. En realidad es la cantidad de azúcar la que causa ambos. No confundir la idea de correlación con el concepto de causalidad. El hecho de que dos variables estén correlacionadas no significa que una haga que la otra suceda.

Ejemplo\(\PageIndex{2}\) correlation versus Causation

1. Un estudio mostró una fuerte correlación lineal entre el consumo per cápita de cerveza y los salarios de los maestros. ¿Dar un aumento a un maestro hace que la gente compre más cerveza? ¿Comprar más cerveza hace que los maestros obtengan un aumento?
2. Un estudio muestra que existe una correlación entre las personas que han tenido un conducto radicular y las que tienen cáncer. ¿Eso significa que tener un conducto radicular causa cáncer?

Solución

a. Probablemente haya algún otro factor que haga que ambos aumenten al mismo tiempo. Piensa en esto: En un pueblo donde la gente tiene poco dinero extra, no van a tener dinero para la cerveza y no van a dar subidas a los maestros. En otro pueblo donde la gente tiene más dinero extra para gastar les será más fácil comprar más cerveza y estarían más dispuestos a dar a los maestros plantea.

b. El hecho de que haya correlación positiva no significa que una causó la otra. Resulta que existe una correlación positiva entre comer zanahorias y cáncer, pero eso no significa que comer zanahorias cause cáncer. En otras palabras, hay muchas relaciones que puedes encontrar entre dos variables, pero eso no significa que una causó la otra.

Recuerde que una correlación solo significa que existe un patrón. No significa que una variable haga que la otra variable cambie.

Variación Explicada

Como se indicó anteriormente, existe cierta variabilidad en los valores de las variables dependientes, como las calorías. Parte de la variación en calorías se debe al contenido de alcohol y otras se deben a otros factores. ¿Qué tanto de la variación en las calorías se debe al contenido de alcohol?

Al considerar esta pregunta, se quiere ver qué tanto de la variación en calorías se explica por el contenido de alcohol y cuánto se explica por otras variables. Date cuenta de que algunos de los cambios en calorías tienen que ver con otros ingredientes. Se pueden tomar dos cervezas con el mismo contenido de alcohol, pero la cerveza una tiene mayores calorías debido a los demás ingredientes. Alguna variabilidad se explica por el modelo y alguna variabilidad no se explica. Juntos, ambos dan la variabilidad total. Esto es

\(\begin{array}{ccccc} {\text{(total variation)}}&{=}&{\text{(explained variation)}}&{+}&{\text{(unexplained variation)}}\\ {\sum(y-\overline{y})^{2}}&{=}& {\sum(\hat{y}-\overline{y})^{2}}&{+}&{\sum(y-\hat{y})^{2}} \end{array}\)

Nota

La proporción de la variación que se explica por el modelo es

\(r^{2}=\dfrac{\text { explained variation }}{\text { total variation }}\)

Esto se conoce como el coeficiente de determinación.

Para encontrar el coeficiente de determinación, se cuadra el coeficiente de correlación. Además, forma parte\(r^{2}\) de los resultados de la calculadora.

Ejemplo\(\PageIndex{3}\) finding the coefficient of determination

Encuentra el coeficiente de variación en calorías que se explica por la relación lineal entre el contenido de alcohol y las calorías e interpreta el valor.

Solución

De los resultados de la calculadora,

\(r^{2} = 0.8344\)

Usando R, puede hacer (cor (variable independiente, variable dependiente)) ^2. Entonces eso sería (cor (alcohol, calorías)) ^2, y la salida sería

[1] 0.8343751

O simplemente puedes usar una calculadora y cuadrar el valor de correlación.

Así, 83.44% de la variación en calorías se explica a la relación lineal entre el contenido de alcohol y las calorías. El otro 16.56% de la variación se debe a otros factores. Un coeficiente de determinación realmente bueno tiene una parte muy pequeña, inexplicable.

y\(r^{2}\)

¿Qué tan fuerte es la relación entre el contenido de alcohol y la cantidad de calorías en la cerveza de 12 onzas? Para determinar si existe una correlación lineal positiva, se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza para varias cervezas diferentes (“Calorías en cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{1}\). Encuentra el coeficiente de correlación y el coeficiente de determinación usando la fórmula.

Solución

A partir del Ejemplo\(\PageIndex{2}\),\(S S_{x}=12.45, S S_{y}=10335.5556, S S_{x y}=327.6667\)

Coeficiente de correlación:

\(r=\dfrac{S S_{x y}}{\sqrt{S S_{x} S S_{y}}}=\dfrac{327.6667}{\sqrt{12.45 * 10335.5556}} \approx 0.913\)

Coeficiente de determinación:

\(r^{2}=(r)^{2}=(0.913)^{2} \approx 0.834\)

Ahora que tienes un coeficiente de correlación, ¿cómo puedes saber si es significativo o no? Esto se responderá en la siguiente sección.

Testo

Ejercicio\(\PageIndex{1}\)

Para cada problema, indicar las variables aleatorias. Además, mira para ver si hay algún valor atípico que necesite ser eliminado. Hacer el análisis de correlación con y sin los puntos atípicos sospechosos para determinar si su eliminación afecta la correlación. Los conjuntos de datos de esta sección se encuentran en la sección 10.1 y se utilizarán en la sección 10.3.

1. Cuando un antropólogo encuentra restos esqueléticos, necesita averiguar la altura de la persona. Se recolectaron la altura de una persona (en cm) y la longitud de su hueso metacarpiano 1 (en cm) y se encuentran en Ejemplo\(\PageIndex{5}\) (“Predicción de altura”, 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
2. Ejemplo\(\PageIndex{6}\) contiene el valor de la casa y la cantidad de ingresos por alquiler en un año que la casa aporta (“Capital y renta”, 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
3. El Banco Mundial recopila información sobre la esperanza de vida de una persona en cada país (“Esperanza de vida en,” 2013) y la tasa de fecundidad por mujer en el país (“Tasa de fertilidad”, 2013). Los datos de 24 países seleccionados al azar para el año 2011 se encuentran en Ejemplo\(\PageIndex{7}\). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
4. El Banco Mundial recopiló datos sobre el porcentaje del PIB que un país gasta en gastos de salud (“Gasto de salud”, 2013) y también el porcentaje de mujeres que reciben atención prenatal (“Mujer embarazada que recibe”, 2013). Los datos de los países donde esta información está disponible para el año 2011 se encuentran en Ejemplo\(\PageIndex{8}\). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
5. La altura y el peso de los beisbolistas están en Ejemplo\(\PageIndex{9}\) (“MLB heightsweights,” 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
6. Diferentes especies tienen diferentes pesos corporales y pesos cerebrales están en Ejemplo\(\PageIndex{10}\). (“Brain2BodyWeight”, 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
7. Se tomó una muestra aleatoria de hotdogs de carne y se midió la cantidad de sodio (en mg) y calorías. (“Data hotdogs”, 2013) Los datos están en Ejemplo\(\PageIndex{11}\). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
8. El ingreso per cápita en 1960 dólares para los países europeos y el porcentaje de la fuerza laboral que trabaja en la agricultura en 1960 están en Ejemplo\(\PageIndex{12}\) (“Desarrollo económico de la OCDE”, 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
9. El tabaquismo y el cáncer se han relacionado. El número de muertes por cien mil por cáncer de vejiga y el número de cigarrillos vendidos per cápita en 1960 se encuentran en Ejemplo\(\PageIndex{13}\) (“Fumar y cáncer”, 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
10. El peso de un automóvil puede influir en el kilometraje que pueda obtener el automóvil. Se recolectó una muestra aleatoria de pesos y kilometraje de los autos y se encuentran en Ejemplo\(\PageIndex{14}\) (“Kilometraje de autos de pasajeros”, 2013). Encontrar el coeficiente de correlación y el coeficiente de determinación y luego interpretar ambos.
11. Existe una correlación negativa entre el gasto policial y la tasa delictiva. ¿Significa esto que gastar más dinero en policías hace que disminuya la tasa delictiva? Explica tu respuesta.
12. Existe una correlación positiva entre la venta de tabaco y la venta de alcohol. ¿Significa eso que consumir tabaco hace que una persona también beba alcohol? Explica tu respuesta.
13. Existe una correlación positiva entre la temperatura promedio en un lugar y la tasa de moralidad por cáncer de mama. ¿Significa eso que temperaturas más altas hacen que más mujeres mueran por cáncer de mama? Explica tu respuesta.
14. Existe una correlación positiva entre el tiempo que una empresa de vajillas pule un plato y el precio del plato. ¿Significa eso que el tiempo que se pule un plato determina el precio del plato? Explica tu respuesta.

Contestar

Sólo se dan el coeficiente de correlación y el coeficiente de determinación. Ver soluciones para toda la respuesta.

1. r = 0.9578,\(r^{2}\) = 0.7357

3. r = -0.9313,\(r^{2}\) = 0.8674

5. r = 0.6605,\(r^{2}\) = 0.4362

7. r = 0.8871,\(r^{2}\) = 0.7869

9. r = 0.7036,\(r^{2}\) = 0.4951

11. No, vea soluciones.

13. No, vea soluciones.