10.3: Inferencia para Regresión y Correlación
- Page ID
- 149833
¿Cómo se dice realmente que tiene una correlación? ¿Se puede probar para ver si realmente hay una correlación? Por supuesto, la respuesta es sí. La prueba de hipótesis para la correlación es la siguiente:
Prueba de Hipótesis para Correlación:
- Declarar las variables aleatorias en palabras.
x = variable independiente
y = variable dependiente - Indique las hipótesis nulas y alternativas y el nivel de significación
\(\begin{array}{l}{H_{o} : \rho=0 \text { (There is no correlation) }} \\ {H_{A} : \rho \neq 0 \text { (There is a correlation) }} \\ {\text { or }} \\ {H_{A} : \rho<0 \text { (There is a negative correlation) }} \\ {\text { or }} \\ {H_{A} : \rho>0 \text { (There is a postive correlation) }}\end{array}\)
También, indique aquí su\(\alpha\) nivel. - Indicar y verificar los supuestos para la prueba de hipótesis
Los supuestos para la prueba de hipótesis son los mismos supuestos para regresión y correlación. - Encuentra el estadístico de prueba y el valor p
\(t=\dfrac{r}{\sqrt{\dfrac{1-r^{2}}{n-2}}}\)
con grados de libertad = df = n - 2
p-valor: Usando el TI-83/84: tcdf (límite inferior, límite superior, df)Nota
Si\(H_{A} : \rho<0\), entonces el límite inferior es -1E99 y el límite superior es su estadística de prueba. Si\(H_{A} : \rho>0\), entonces el límite inferior es su estadística de prueba y el límite superior es 1E99. Si\(H_{A} : \rho \neq 0\), entonces encuentra el valor p para\(H_{A} : \rho<0\), y multiplica por 2.
Usando R: pt (t, df)
Nota
Si\(H_{A} : \rho<0\), entonces usa pt (t, df), Si\(H_{A} : \rho>0\), luego usa\(1-\mathrm{pt}(t, d f)\). Si\(H_{A} : \rho \neq 0\), entonces encuentra el valor p para\(H_{A} : \rho<0\), y multiplica por 2.
- Conclusión
Aquí es donde escribes rechazar\(H_{o}\) o no rechazar\(H_{o}\). La regla es: si el valor p <\(\alpha\), entonces rechazar\(H_{o}\). Si el valor p\(\geq \alpha\), entonces no puede rechazar\(H_{o}\). - Interpretación
Aquí es donde interpretas en términos del mundo real la conclusión a la prueba. La conclusión para una prueba de hipótesis es que o bien tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad, o no tienes suficiente evidencia para demostrar que\(H_{A}\) es verdad.
Nota
Los resultados de la calculadora TI-83/84 te dan el estadístico de prueba y el valor p. En R, el comando para obtener el estadístico de prueba y el valor p es cor.test (variable independiente, variable dependiente, alternativa = “menor” o “mayor”). Usar menos para\(H_{A} : \rho<0\), usar mayor para\(H_{A} : \rho>0\), y dejar fuera este comando para\(H_{A} : \rho \neq 0\).
Ejemplo\(\PageIndex{1}\) Testing the claim of a linear correlation
¿Existe una correlación positiva entre el contenido de alcohol de la cerveza y las calorías? Para determinar si existe una correlación lineal positiva, se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza para varias cervezas diferentes (“Calorías en la cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{1}\). Prueba al nivel del 5%.
Solución
- Declarar las variables aleatorias en palabras.
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas - Indicar las hipótesis nulas y alternativas y el nivel de significación.
Ya que se le pregunta si hay una correlación positiva,\(\rho> 0\).
\(\begin{array}{l}{H_{o} : \rho=0} \\ {H_{A} : \rho>0} \\ {\alpha=0.05}\end{array}\) - Indicar y verificar los supuestos para la prueba de hipótesis.
Los supuestos para la prueba de hipótesis ya se verificaron en Ejemplo\(\PageIndex{2}\). - Encuentra el estadístico de prueba y el valor p.
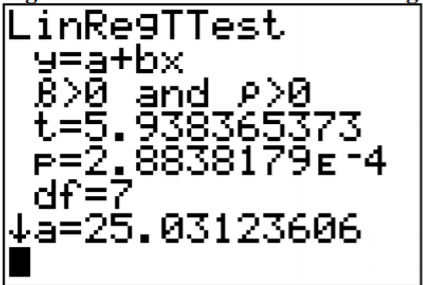
Los resultados de la calculadora TI-83/84 están en la Figura\(\PageIndex{1}\).
.png)
Figura\(\PageIndex{1}\): Resultados para la Prueba de Regresión Lineal en TI-83/84 Estadística de
prueba: t\(\approx\) 5.938 y valor p:\(p \approx 2.884 \times 10^{-4}\)
Los resultados de R son
cor.test (alcohol, calorías, alternativa = “mayor”)
Datos de correlación producto-momento de
Pearson: alcohol y calorías
t = 5.9384, df = 7, valor p = 0.0002884 hipótesis
alternativa: la correlación verdadera es mayor que 0
Intervalo de confianza del 95 por ciento:
0.7046161 1.0000000 Estimaciones
muestrales:
cor
0.9134414 Estadística de
prueba: t\(\approx\) 5.9384 y valor p:\(p \approx 0.0002884\) - Conclusión
Rechazar\(H_{o}\) ya que el valor p es menor a 0.05. - Interpretación
Existe evidencia suficiente para demostrar que existe una correlación positiva entre el contenido de alcohol y el número de calorías en una botella de cerveza de 12 onzas.
Intervalo de predicción
Usando la ecuación de regresión puedes predecir el número de calorías a partir del contenido de alcohol. Sin embargo, solo encuentras un valor. El problema es que las cervezas varían un poco en calorías aunque tengan el mismo contenido de alcohol. Sería bueno tener un rango en lugar de un solo valor. El rango se denomina intervalo de predicción. Para encontrar esto, es necesario averiguar cuánto error hay en la estimación a partir de la ecuación de regresión. Esto se conoce como el error estándar de la estimación.
Definición
Error estándar de la estimación
Esta es la suma de cuadrados de los residuos
\(s_{e}=\sqrt{\dfrac{\sum(y-\hat{y})^{2}}{n-2}}\)
Es difícil trabajar con esta fórmula, por lo que hay una fórmula más fácil. También se puede encontrar el valor de la tecnología, como la calculadora.
\(s_{e}=\sqrt{\dfrac{S S_{y}-b^{*} S S_{x y}}{n-2}}\)
Ejemplo\(\PageIndex{2}\) finding the standard error of the estimate
Encuentra el error estándar de la estimación para los datos de cerveza. Para determinar si existe una correlación lineal positiva, se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza para varias cervezas diferentes (“Calorías en cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{1}\).
Solución
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas
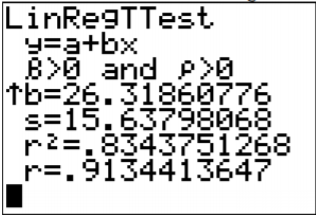
Usando el TI-83/84, los resultados están en la Figura\(\PageIndex{2}\).
.png)
El s en los resultados es el error estándar de la estimación. Entonces\(s_{e} \approx 15.64\).
Para encontrar el error estándar de la estimación en R, los comandos son
lm.out = lm (variable dependiente ~ variable independiente) — esto define el modelo lineal con un nombre para que pueda usarlo más adelante. Luego
resumen (lm.out) — esto producirá la mayor parte de la información que necesita para un análisis de regresión y correlación. De hecho, lo único que R no produce con este comando es el coeficiente de correlación. De lo contrario, puede usar el comando para encontrar la ecuación de regresión, el coeficiente de determinación, el estadístico de prueba, el valor p para una prueba de dos colas y el error estándar de la estimación.
Los resultados de R son
lm.out=lm (calories~alcohol)
resumen (lm.out)
Llamar:
lm (fórmula = calorías ~ alcohol)
Residuales:
\(\begin{array} {ccccc} {\text{Min}} & {\text{1Q}} & {\text{Median}} & {\text{3Q}} & {\text{Max}} \\{-30.253}&{-1.624}&{2.744}&{9.271}&{14.271} \end{array}\)
Coeficientes:
\(\begin{array}{ccccc} {}&{\text{Estimate Std.}}&{\text{Error}}&{\text{t value}}&{\text{Pr(>|t|)}} \\ {\text{(Intercept)}}&{25.031}&{24.999}&{1.001}&{0.350038}\\{\text{alcohol}}&{26.319}&{4.432}&{5.938}&{0.000577}\end{array}\)
—
Signif. códigos: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1
Error estándar residual: 15.64 en 7 grados de libertad
Múltiples R cuadrados: 0.8344, R al cuadrado ajustado: 0.8107
Estadístico F: 35.26 en 1 y 7 DF, valor p: 0.0005768
De esta salida, se puede encontrar la intercepción y es 25.031, la pendiente es 26.319, el estadístico de prueba es t = 5.938, el valor p para la prueba de dos colas es 0.000577. Si desea el valor p para una prueba de una cola, divida este número por 2. El error estándar de la estimación es el error estándar residual y es 15.64. Hay alguna información en esta salida que no necesitas.
Si quieres saber cómo calcular el error estándar de la estimación a partir de la fórmula, consulta Ejemplo\(\PageIndex{3}\).
Ejemplo\(\PageIndex{3}\) finding the standard error of the estimate from the formula
Encuentra el error estándar de la estimación para los datos de cerveza usando la fórmula. Para determinar si existe una correlación lineal positiva, se tomó una muestra aleatoria del contenido de alcohol y calorías de la cerveza para varias cervezas diferentes (“Calorías en cerveza”, 2011), y los datos están en Ejemplo\(\PageIndex{1}\).
Solución
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas
De Ejemplo\(\PageIndex{3}\):
\(\begin{array}{l}{S S_{y}=\sum(y-\overline{y})^{2}=10335.56} \\ {S S_{x y}=\sum(x-\overline{x})(y-\overline{y})=327.6666} \\ {n=9} \\ {b=26.3}\end{array}\)
El error estándar de la estimación es
\(\begin{aligned} s_{e} &=\sqrt{\dfrac{S S_{y}-b^{*} S S_{x y}}{n-2}} \\ &=\sqrt{\dfrac{10335.56-26.3(327.6666)}{9-2}} \\ &=15.67 \end{aligned}\)
Intervalo de predicción para un individuo y
Dado el valor fijo\(x_{0}\), el intervalo de predicción para una y individual es
\(\hat{y}-E<y<\hat{y}+E\)
donde
\(\begin{array}{l}{\hat{y}=a+b x} \\ {E=t_{c} s_{e} \sqrt{1+\dfrac{1}{n}+\dfrac{\left(x_{o}-\overline{x}\right)^{2}}{S S_{x}}}} \\ {d f=n-2}\end{array}\)
Nota
Para\(S S_{x}=\sum(x-\overline{x})^{2}\) recordar, la fórmula de derivación estándar del capítulo 3\(s_{x}=\sqrt{\dfrac{\sum(x-\overline{x})^{2}}{n-1}}\)
Entonces,\(s_{x}=\sqrt{\dfrac{S S_{x}}{n-1}}\)
Ahora soluciona para\(S S_{x}\)
\(S S_{x}=s_{x}^{2}(n-1)\)
Puede obtener la desviación estándar de la tecnología.
R producirá el intervalo de predicción para usted. Los comandos son (Tenga en cuenta que probablemente ya hizo el comando lm.out. No es necesario que vuelva a hacerlo.)
lm.out = lm (variable dependiente ~ variable independiente) — calcula el modelo lineal
predict (lm.out, newdata=list (variable independiente = valor), interval="predicción”, level=C) — calculará un intervalo de predicción para la variable independiente establecida en un valor particular (poner eso valor en lugar de la palabra valor), en un nivel C particular (dado como decimal)
Ejemplo\(\PageIndex{4}\) find the prediction interval
Encuentre un intervalo de predicción del 95% para el número de calorías cuando el contenido de alcohol sea de 6.5% usando una muestra aleatoria tomada del contenido de alcohol y calorías de la cerveza (“Calorías en la cerveza”, 2011). Los datos están en Ejemplo\(\PageIndex{1}\).
Solución
x = contenido de alcohol en la cerveza
y = calorías en cerveza de 12 onzas
Calcular el intervalo de predicción usando la calculadora TI-83/84:
De Ejemplo\(\PageIndex{2}\)
\(\begin{array}{l}{\hat{y}=25.0+26.3 x} \\ {x_{o}=6.50} \\ {\hat{y}=25.0+26.3(6.50)=196 \text { calories }}\end{array}\)
Del Ejemplo #10 .3.2
\(s_{e} \approx 15.64\)
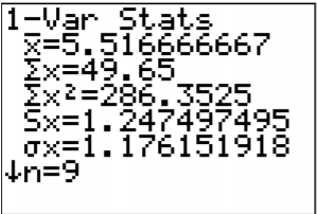.png)
\(\begin{array}{l}{\overline{x}=5.517} \\ {s_{x}=1.247497495} \\ {n=9}\end{array}\)
Ahora puedes encontrar
\(\begin{aligned} S S_{x} &=s_{x}^{2}(n-1) \\ &=(1.247497495)^{2}(9-1) \\ &=12.45 \\ d f &=n-2=9-2=7 \end{aligned}\)
Ahora mira en la tabla A.2. Bajar la primera columna a 7, luego pasar a la columna encabezada con 95%.
\(t_{c}=2.365\)
\(\begin{aligned} E &=t_{c} s_{e} \sqrt{1+\dfrac{1}{n}+\dfrac{\left(x_{o}-\overline{x}\right)^{2}}{S S_{x}}} \\ &=2.365(15.64) \sqrt{1+\dfrac{1}{9}+\dfrac{(6.50-5.517)^{2}}{12.45}} \\ &=40.3 \end{aligned}\)
El intervalo de predicción es
\(\begin{array}{l}{\hat{y}-E<y<\hat{y}+E} \\ {196-40.3<y<196+40.3} \\ {155.7<y<236.3}\end{array}\)
Calcular el intervalo de predicción usando R:
predict (lm.out, newdata=list (alcohol=6.5), interval = “predicción”, level=0.95)
\(\begin{array}{ccc}{}&{\text { fit }} & {\text { lwr }} & {\text { upr }} \\ {1} & {196.1022} & {155.7847}&{236 .4196}\end{array}\)
fit =\(\hat{\mathcal{Y}}\) cuando x = 6.5%. lwr = límite inferior del intervalo de predicción. upr = límite superior del intervalo de predicción. Entonces el intervalo de predicción es\(155.8<y<236.4\).
Interpretación estadística: Existe un 95% de probabilidad de que el intervalo\(155.8<y<236.4\) contenga el valor verdadero de las calorías cuando el contenido de alcohol sea de 6.5%.
Interpretación del mundo real: Si una cerveza tiene un contenido de alcohol de 6.50% entonces tiene entre 156 y 236 calorías.
Ejemplo\(\PageIndex{5}\) Doing a correlation and regression analysis using the ti-83/84
Ejemplo\(\PageIndex{1}\) contiene altas temperaturas seleccionadas al azar en varias ciudades en un solo día y la elevación de la ciudad.
| Elevación (en pies) | 7000 | 4000 | 6000 | 3000 | 7000 | 4500 | 5000 |
|---|---|---|---|---|---|---|---|
| Temperatura (°F) | 50 | 60 | 48 | 70 | 55 | 55 | 60 |
- Declarar las variables aleatorias.
- Encuentre una ecuación de regresión para elevación y temperatura alta en un día determinado.
- Encuentra los residuos y crea una parcela residual.
- Utilice la ecuación de regresión para estimar la temperatura alta en ese día a una elevación de 5500 pies.
- Utilice la ecuación de regresión para estimar la temperatura alta en ese día a una elevación de 8000 pies.
- Entre las respuestas a las partes d y e, ¿cuál estimación es probablemente más precisa y por qué?
- Encuentra el coeficiente de correlación y el coeficiente de determinación e interpreta ambos.
- ¿Hay evidencia suficiente para mostrar una correlación negativa entre elevación y alta temperatura? Prueba al nivel del 5%.
- Encuentra el error estándar de la estimación.
- Usando un intervalo de predicción del 95%, encuentre un rango para alta temperatura para una elevación de 6500 pies.
Solución
a. x = elevación
y = alta temperatura
b.
- Se tomó una muestra aleatoria como se indica en el problema.
- La distribución para cada valor de alta temperatura se distribuye normalmente para cada valor de elevación.
- Observe el diagrama de dispersión de alta temperatura versus elevación.
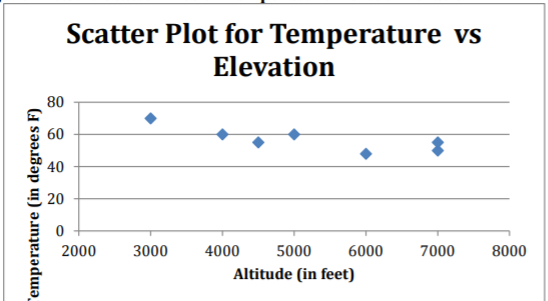.png)
Figura\(\PageIndex{4}\): Gráfica de dispersión de temperatura versus elevación
La gráfica de dispersión se ve bastante lineal. - No hay puntos que parezcan ser valores atípicos.
- La gráfica residual para temperatura versus elevación parece ser bastante aleatoria. (Ver Figura\(\PageIndex{7}\).)
Parece que la alta temperatura se distribuye normalmente.
- Observe el diagrama de dispersión de alta temperatura versus elevación.
Todos los cálculos se computaron utilizando la calculadora TI-83/84.
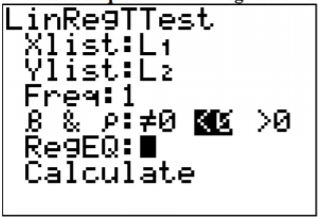.png)
.png)
\(\hat{y}=77.4-0.0039 x\)
c.
| x | y | \(\hat{\mathcal{Y}}\) | \(y-\hat{y}\) |
|---|---|---|---|
| 7000 | 50 | \ (\ hat {\ mathcal {Y}}\) ">50.1 | \ (y-\ hat {y}\) ">-0.1 |
| 4000 | 60 | \ (\ hat {\ mathcal {Y}}\) ">61.8 | \ (y-\ hat {y}\) ">-1.8 |
| 6000 | 48 | \ (\ hat {\ mathcal {Y}}\) ">54.0 | \ (y-\ hat {y}\) ">-6.0 |
| 3000 | 70 | \ (\ hat {\ mathcal {Y}}\) ">65.7 | \ (y-\ hat {y}\) ">4.3 |
| 7000 | 55 | \ (\ hat {\ mathcal {Y}}\) ">50.1 | \ (y-\ hat {y}\) ">4.9 |
| 4500 | 55 | \ (\ hat {\ mathcal {Y}}\) ">59.85 | \ (y-\ hat {y}\) ">-4.85 |
| 5000 | 60 | \ (\ hat {\ mathcal {Y}}\) ">57.9 | \ (y-\ hat {y}\) ">2.1 |
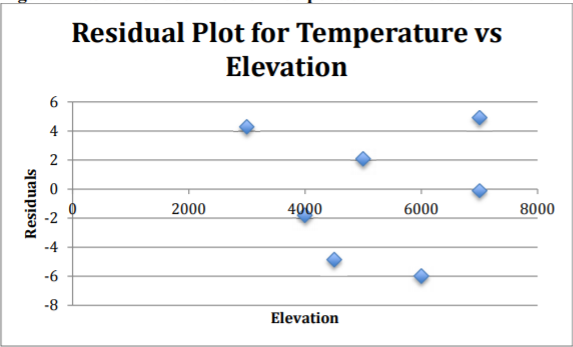.png)
Los residuos parecen ser bastante aleatorios.
d.
\(\begin{array}{l}{x_{o}=5500} \\ {\hat{y}=77.4-0.0039(5500)=55.95^{\circ} F}\end{array}\)
e.
\(\begin{array}{l}{x_{o}=8000} \\ {\hat{y}=77.4-0.0039(8000)=46.2^{\circ} F}\end{array}\)
f. La parte d es más precisa, ya que es interpolación y la parte e es extrapolación.
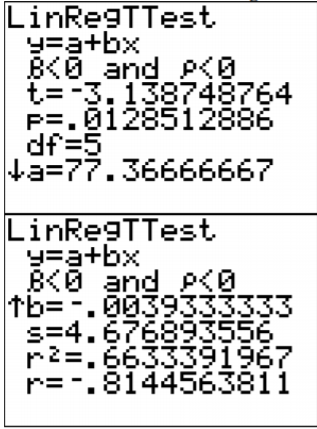
g. De la Figura\(\PageIndex{6}\), el coeficiente de correlación es r\(\approx\) -0.814, que es moderada a fuerte correlación negativa.
De la Figura\(\PageIndex{6}\), el coeficiente de determinación es\(r^{2} \approx 0.663\), lo que significa que 66.3% de la variabilidad en alta temperatura se explica por el modelo lineal. El otro 33.7% se explica por otras variables como las condiciones climáticas locales.
h.
- Declarar las variables aleatorias en palabras.
x = elevación
y = temperatura alta - Indicar las hipótesis nulas y alternativas y el nivel de significación
\(\begin{array}{l}{H_{o} : \rho=0} \\ {H_{A} : \rho<0} \\ {\alpha=0.05}\end{array}\) - Indicar y verificar los supuestos para la prueba de hipótesis Los supuestos para la prueba de hipótesis ya se verificaron parte b.
- Encuentre el estadístico de prueba y el valor p
De la Figura\(\PageIndex{6}\), Estadística de
prueba:
\(t \approx-3.139\)
valor p:
\(p \approx 0.0129\) - Conclusión
Rechazar\(H_{o}\) ya que el valor p es menor a 0.05. - Interpretación
Existe evidencia suficiente para mostrar que existe una correlación negativa entre la elevación y las altas temperaturas.
i. De la Figura\(\PageIndex{6}\),
\(s_{e} \approx 4.677\)
j.\(\hat{y}=77.4-0.0039(6500) \approx 52.1^{\circ} F\)
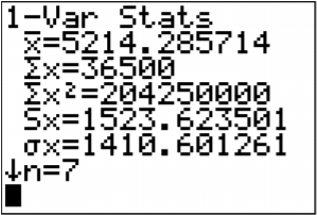.png)
\(\begin{array}{l}{\overline{x}=5214.29} \\ {s_{x}=1523.624} \\ {n=7}\end{array}\)
Ahora puedes encontrar
\(\begin{aligned} S S_{x} &=s_{x}^{2}(n-1) \\ &=(1523.623501)^{2}(7-1) \\ &=13928571.43 \\ d f &=n-2=7-2=5 \end{aligned}\)
Ahora mira en la tabla A.2. Bajar la primera columna a 5, luego pasar a la columna encabezada con 95%.
\(t_{c}=2.571\)
Entonces
\(\begin{aligned} E &=t_{c} s_{e} \sqrt{1+\dfrac{1}{n}+\dfrac{\left(x_{o}-\overline{x}\right)^{2}}{S S_{x}}} \\ &=2.571(4.677) \sqrt{1+\dfrac{1}{7}+\dfrac{(6500-5214.29)^{2}}{13928571.43}} \\ &=13.5 \end{aligned}\)
El intervalo de predicción es
\(\begin{array}{l}{\hat{y}-E<y<\hat{y}+E} \\ {52.1-13.5<y<52.1+13.5} \\ {38.6<y<65.6}\end{array}\)
Interpretación estadística: Existe un 95% de probabilidad de que el intervalo\(38.6<y<65.6\) contenga el valor verdadero para la temperatura a una elevación de 6500 pies.
Interpretación del mundo real: Una ciudad de 6500 pies tendrá una temperatura alta entre 38.6°F y 65.6°F Aunque este intervalo es bastante amplio, al menos el intervalo te dice que la temperatura no es tan cálida.
Ejemplo\(\PageIndex{6}\) doing a correlation and regression analysis using r
Ejemplo\(\PageIndex{1}\) contiene altas temperaturas seleccionadas al azar en varias ciudades en un solo día y la elevación de la ciudad.
- Declarar las variables aleatorias.
- Encuentre una ecuación de regresión para elevación y temperatura alta en un día determinado.
- Encuentra los residuos y crea una parcela residual.
- Utilice la ecuación de regresión para estimar la temperatura alta en ese día a una elevación de 5500 pies.
- Utilice la ecuación de regresión para estimar la temperatura alta en ese día a una elevación de 8000 pies.
- Entre las respuestas a las partes d y e, ¿cuál estimación es probablemente más precisa y por qué?
- Encuentra el coeficiente de correlación y el coeficiente de determinación e interpreta ambos.
- ¿Hay evidencia suficiente para mostrar una correlación negativa entre elevación y alta temperatura? Prueba al nivel del 5%.
- Encuentra el error estándar de la estimación.
- Usando un intervalo de predicción del 95%, encuentre un rango para alta temperatura para una elevación de 6500 pies.
Solución
a. x = elevación
y = alta temperatura
b.
- Se tomó una muestra aleatoria como se indica en el problema.
- La distribución para cada valor de alta temperatura se distribuye normalmente para cada valor de elevación.
- Observe el diagrama de dispersión de alta temperatura versus elevación.
comando R: plot (elevation, temperature, main="Diagrama de dispersión para Temperatura vs Elevación”, xLab="Elevación (pies)”, YLab="Temperatura (grados F)”, ylim=c (0,80))
.png)
Figura\(\PageIndex{9}\): Gráfica de dispersión de Temperatura Versus Elevación
El gráfico de dispersión se ve bastante lineal. - La gráfica residual para temperatura versus elevación parece ser bastante aleatoria. (Ver Figura 10.3.10.)
Parece que la alta temperatura se distribuye normalmente.
- Observe el diagrama de dispersión de alta temperatura versus elevación.
Uso de R:
Comandos:
lm.out=lm (temperatura ~ elevación)
resumen (lm.out)
Salida:
Llamada:
lm (fórmula = temperatura ~ elevación)
Residuales:
\(\begin{array} {ccccccc} {1}&{2}&{3}&{4}&{5}&{6}&{7}\\{ 0.1667}&{-1.6333}&{-5.7667}&{4 .4333}&{5 .1667}&{-4.6667}&{ 2.3000} \end{array}\)
Coeficientes:
\(\begin{array}{ccccc} {}&{\text{Estimate Std.}}&{\text{Error}}&{\text{t value}}&{\text{Pr(>|t|)}} \\ {\text{(Intercept)}}&{77.36667}&{6.769182}&{11.429}&{8.98e-05 ***}\\{\text{elevation}}&{-0.003933}&{0.001253}&{-3.139}&{0.0257*}\end{array}\)
— Códigos medios: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 '' 1 Error estándar
residual: 4.677 en 5 grados de libertad R
múltiple al cuadrado: 0.6633, R al cuadrado ajustado: 0.596
Estadístico F: 9.852 sobre 1 y 5 DF, valor p: 0.0257
De la salida se puede ver la pendiente = -0.0039 y la intercepción y = 77.4. Entonces la ecuación de regresión es:
\(\hat{y}=77.4-0.0039 x\)
c. comando R: (observe que estos también están en la salida summary (lm.out), pero si tiene demasiados puntos de datos, entonces R solo da un resumen numérico de los residuos.)
residuos (lm.out)
\(\begin{array} {CCCCCCC} {1}&{2}&{3}&{4}&{5}&{6}&{7} \\ {0.1666667}&{-1.63333333}&{-5.766667}&{4 .43333333}&{5 .1666667}&{-4.66666667}&{2.3000000} \end{array}\)
Entonces para la primera x de 7000, el residual es aproximadamente 0.1667. Esto significa que si encuentras el\(\hat{y}\) for cuando x es 7000 y luego restas esta respuesta del valor y de 50 que se midió, obtendrías 0.1667. Proceso similar se calcula para los otros valores residuales.
Para trazar los residuos, el comando R es
plot (elevación, residuales (lm.out), principal="Parcela residual para Temperautre vs Elevation”, xlab="Elevación (pies)”, ylab="Residuales”)
abline (0,0)
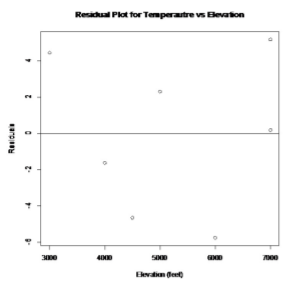.png)
Los residuos parecen ser bastante aleatorios.
d.\(\begin{array}{l}{x_{o}=5500} \\ {\hat{y}=77.4-0.0039(5500)=55.95^{\circ} F}\end{array}\)
e.\(\begin{array}{l}{x_{o}=8000} \\ {\hat{y}=77.4-0.0039(8000)=46.2^{\circ} F}\end{array}\)
f. La parte d es más precisa, ya que es interpolación y la parte e es extrapolación.
g. El comando R para el coeficiente de correlación es
cor (elevación, temperatura)
[1] -0.8144564
Entonces,\(r \approx-0.814\), que es moderada a fuerte correlación negativa.
A partir del resumen (lm.out), el coeficiente de determinación es el Múltiple R-cuadrado.
Entonces\(r^{2} \approx 0.663\), lo que significa que 66.3% de la variabilidad en altas temperaturas se explica por el modelo lineal. El otro 33.7% se explica por otras variables como las condiciones climáticas locales.
h.
- Declarar las variables aleatorias en palabras.
x = elevación
y = temperatura alta - . Indicar las hipótesis nulas y alternativas y el nivel de significación
\(\begin{array}{l}{H_{o} : \rho=0} \\ {H_{A} : \rho<0} \\ {\alpha=0.05}\end{array}\) - Indicar y verificar los supuestos para la prueba de hipótesis.
Los supuestos para la prueba de hipótesis ya se verificaron parte b. - Encuentra el estadístico de prueba y
el valor p El comando R es cor.test (elevación, temperatura, alternativa = “menos”)
Datos de correlación producto-momento de
Pearson: elevación y temperatura
t = -3.1387, df = 5, valor p = 0.01285
hipótesis alternativa: correlación verdadera es menor de 0
95 por ciento intervalo de confianza:
-1.0000000 -0.3074247 estimaciones de
muestra:
cor
-0.8144564 Estadística de
prueba:\(t \approx-3.1387\) y valor p:\(p \approx 0.01285\) - Conclusión
Rechazar\(H_{o}\) ya que el valor p es menor a 0.05. - Interpretación
Existe evidencia suficiente para mostrar que existe una correlación negativa entre la elevación y las altas temperaturas.
i. Del resumen (lm.out), Error estándar residual: 4.677.
Entonces,\(s_{e} \approx 4.677\)
j. R comando es predecir (lm.out, newdata=list (elevación = 6500), intervalo = “predicción”, nivel=0.95)
\(\begin{array}{cccc}{}&{\text { fit }}&{ \text { lwr} } &{ \text { upr }} \\ {1}&{51.8}&{38 .29672}&{65 .30328}\end{array}\)
Entonces cuando x = 6500 pies,\(\hat{y}=51.8^{\circ} F \text { and } 38.29672<y<65.30328\).
Interpretación estadística: Existe un 95% de probabilidad de que el intervalo\(38.3<y<65.3\) contenga el valor verdadero para la temperatura a una elevación de 6500 pies.
Interpretación del mundo real: Una ciudad de 6500 pies tendrá una temperatura alta entre 38.3°F y 65.3°F Aunque este intervalo es bastante amplio, al menos el intervalo te dice que la temperatura no es tan cálida.
Testo
Ejercicio\(\PageIndex{1}\)
Para cada problema, indique las variables aleatorias. Los conjuntos de datos de esta sección están en la tarea para la sección 10.1 y también se utilizaron en la sección 10.2. Si eliminaste algún punto de datos como valores atípicos en las otras secciones, elimínalos también en esta sección tarea.
- Cuando un antropólogo encuentra restos esqueléticos, necesita averiguar la altura de la persona. Se recolectaron la altura de una persona (en cm) y la longitud de su hueso metacarpiano uno (en cm) y se encuentran en Ejemplo\(\PageIndex{5}\) (“Predicción de altura”, 2013).
- Prueba al nivel del 1% para una correlación positiva entre la longitud del hueso metacarpiano uno y la altura de una persona.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 99% para la altura de una persona con una longitud metacarpiano de 44 cm.
- Ejemplo\(\PageIndex{6}\) contiene el valor de la casa y la cantidad de ingresos por alquiler en un año que la casa aporta (“Capital y renta”, 2013).
- Prueba al nivel del 5% para una correlación positiva entre el valor de la casa y el monto del alquiler.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 95% para los ingresos por alquiler de una casa con un valor de $230,000.
- El Banco Mundial recopila información sobre la esperanza de vida de una persona en cada país (“Esperanza de vida en,” 2013) y la tasa de fecundidad por mujer en el país (“Tasa de fertilidad”, 2013). Los datos de 24 países seleccionados al azar para el año 2011 se encuentran en Ejemplo\(\PageIndex{7}\).
- Prueba al nivel del 1% para una correlación negativa entre la tasa de fertilidad y la esperanza de vida.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 99% para la esperanza de vida para un país que tenga una tasa de fecundidad de 2.7.
- El Banco Mundial recopiló datos sobre el porcentaje del PIB que un país gasta en gastos de salud (“Gasto de salud”, 2013) y también el porcentaje de mujeres que reciben atención prenatal (“Mujer embarazada que recibe”, 2013). Los datos de los países donde esta información está disponible para el año 2011 se encuentran en Ejemplo\(\PageIndex{8}\).
- Prueba al nivel del 5% para una correlación entre el porcentaje gastado en el gasto en salud y el porcentaje de mujeres que reciben atención prenatal.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción de 95% para el porcentaje de mujeres que reciben atención prenatal para un país que gasta 5.0% del PIB en gastos de salud.
- La altura y el peso de los beisbolistas están en Ejemplo\(\PageIndex{9}\) (“MLB heightsweights,” 2013).
- Prueba al nivel del 5% para una correlación positiva entre la estatura y el peso de los beisbolistas.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 95% para el peso de un beisbolista que mide 75 pulgadas de alto.
- Diferentes especies tienen diferentes pesos corporales y pesos cerebrales están en Ejemplo\(\PageIndex{10}\). (“Brain2BodyWeight”, 2013).
- Prueba al nivel de 1% para una correlación positiva entre pesos corporales y pesos cerebrales.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 99% para el peso cerebral para una especie que tenga un peso corporal de 62 kg.
- Se tomó una muestra aleatoria de perritos calientes de carne y se midió la cantidad de sodio (en mg) y calorías. (“Data hotdogs”, 2013) Los datos están en Ejemplo\(\PageIndex{11}\).
- Prueba al nivel del 5% para una correlación entre cantidad de calorías y cantidad de sodio.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 95% para la cantidad de sodio que tiene un hotdog de res si es de 170 calorías.
- El ingreso per cápita en 1960 dólares para los países europeos y el porcentaje de la fuerza laboral que trabaja en la agricultura en 1960 están en Ejemplo\(\PageIndex{12}\) (“Desarrollo económico de la OCDE”, 2013).
- Prueba al nivel del 5% para una correlación negativa entre el porcentaje de la fuerza laboral en la agricultura y el ingreso per cápita.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 90% para el ingreso per cápita en un país que tiene 21 por ciento de mano de obra en la agricultura.
- El tabaquismo y el cáncer se han relacionado. El número de muertes por cien mil por cáncer de vejiga y el número de cigarrillos vendidos per cápita en 1960 están en Ejemplo\(\PageIndex{13}\) (“Fumar y cáncer”, 2013).
- Prueba al nivel del 1% para una correlación positiva entre el tabaquismo y las muertes por cáncer de vejiga.
- Encuentra el error estándar de la estimación.
- Calcular un intervalo de predicción del 99% para el número de muertes por cáncer de vejiga cuando las ventas de cigarrillos fueron de 20 per cápita.
- El peso de un automóvil puede influir en el kilometraje que pueda obtener el automóvil. Se recolectó una muestra aleatoria de pesos y kilometraje de los autos y se encuentran en Ejemplo\(\PageIndex{14}\) (“Kilometraje de autos de pasajeros”, 2013).
- Prueba al nivel del 5% para una correlación negativa entre el peso de los autos y el kilometraje.
- Encuentra el error estándar de la estimación.
- Calcule un intervalo de predicción del 95% para el kilometraje en un automóvil que pese 3800 libras.
- Contestar
-
Para la prueba de hipótesis solo se da la conclusión. Ver soluciones para obtener una respuesta completa.
1. a. Rechazar Ho, b.\(s_{e} \approx 4.559\), c.\(151.3161 \mathrm{cm}<y<187.3859 \mathrm{cm}\)
3. a. Rechazar Ho, b.\(s_{e} \approx 3.204\), c.\(62.945 \text { years }<y<81.391 \text{years}\)
5. a. Rechazar Ho, b.\(s_{e} \approx 15.33\), c.\(176.02 \text { inches }<y<240.92 \text{inches}\)
7. a. Rechazar Ho, b.\(s_{e} \approx 48.58\), c.\(348.46 \mathrm{mg}<y<559.38 \mathrm{mg}\)
9. a. Rechazar Ho, b.\(s_{e} \approx 0.6838\), c.\(1.613 \text { hundred thousand }<y<5.432 \text{ hundred thousand}\)
Fuente de datos:
Brain2BodyWeight. (2013, 16 de noviembre). Recuperado a partir de http://wiki.stat.ucla.edu/socr/index...ain2BodyWeight
Calorías en cerveza, alcohol de cerveza, carbohidratos de cerveza. (2011, 25 de octubre). Recuperado a partir de www.beer100.com/beercalories.htm
Valores de capital y renta de propiedades de Auckland. (2013, 26 de septiembre). Recuperado a partir de http://www.statsci.org/data/oz/rentcap.html
Data hotdogs. (2013, 16 de noviembre). Recuperado a partir de http://wiki.stat.ucla.edu/socr/index...D_Data_HotDogs
Tasa de fecundidad. (2013, 14 de octubre). Recuperado a partir de http://data.worldbank.org/indicator/SP.DYN.TFRT.IN
Gasto en salud. (2013, 14 de octubre). Recuperado a partir de http://data.worldbank.org/indicator/SH.XPD.TOTL.ZS
Esperanza de vida al nacer. (2013, 14 de octubre). Recuperado a partir de http://data.worldbank.org/indicator/SP.DYN.LE00.IN
MLB heightsweights. (2013, 16 de noviembre). Recuperado a partir de http://wiki.stat.ucla.edu/socr/index...HeightsWeights
Desarrollo económico de la OCDE. (2013, 04 de diciembre). Recuperado de lib.stat.cmu.edu/dasl/datafiles/oecdat.html
Kilometraje de turismos. (2013, 04 de diciembre). Recuperado de lib.stat.cmu.edu/dasl/datafiles/carmpgdat.html
Predicción de la altura a partir de la longitud del hueso metacarpiano. (2013, 26 de septiembre). Recuperado a partir de http://www.statsci.org/data/general/stature.html
Mujer embarazada que recibe atención prenatal. (2013, 14 de octubre). Recuperado a partir de http://data.worldbank.org/indicator/SH.STA.ANVC.ZS
Tabaquismo y cáncer. (2013, 04 de diciembre). Recuperado de lib.stat.cmu.edu/dasl/datafil... cancerdat.html


