1: Razonamiento Estadístico
- Page ID
- 150383
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tómate un momento para visualizar a la humanidad en su totalidad, desde los primeros humanos hasta el presente. ¿Cómo caracterizarías el bienestar de la humanidad? Piensa más allá de las últimas historias en las noticias. Para ayudar a aclarar, pensar en el tratamiento médico, la vivienda, el transporte, la educación y nuestro conocimiento. Si bien no se puede negar que tenemos algunos problemas que no existían en generaciones anteriores, también tenemos considerablemente más conocimiento.
El progreso que ha logrado la humanidad en el aprendizaje de nosotros mismos, nuestro mundo y nuestro universo ha sido alimentado por el deseo de las personas de resolver problemas u obtener una comprensión. Se ha financiado a través de fondos tanto públicos como privados. Se ha logrado a través de un proceso continuo de personas que proponen teorías y otras que intentan refutar las teorías utilizando la evidencia. Teorías que no son refutadas pasan a formar parte de nuestro conocimiento colectivo. Ninguna persona lo ha logrado, ha sido un esfuerzo colectivo de la humanidad.
Por mucho que sepamos y hayamos logrado, hay mucho que no conocemos y aún no hemos logrado. Hay muchas organizaciones e instituciones diferentes que contribuyen a las ganancias de conocimiento de la humanidad, sin embargo una organización destaca por desafiar a la humanidad para lograr aún más. Esta organización es xPrize.1 En su página web explican que son un motor de innovación. Un facilitador del cambio exponencial. Un catalizador en beneficio de la humanidad”. Esta organización desafía a la humanidad a resolver problemas audaces organizando competiciones y otorgando un premio monetario al equipo ganador. Ejemplos de algunas de sus competencias incluyen:
- 2004: Ansari xPrize (10 millones de dólares) —Private Space Travel— construye una nave espacial confiable, reutilizable, financiada privada y tripulada capaz de transportar a tres personas a 100 kilómetros sobre la superficie de la Tierra dos veces en dos semanas.
- Vigente: The Barbara Bush Foundation Adult Literacy xPrize ($7 millones) - “desafiando a los equipos a desarrollar aplicaciones móviles para dispositivos inteligentes existentes que resulten en el mayor aumento de habilidades de alfabetización entre los alumnos adultos participantes en tan solo 12 meses”.
Se estima que hay 36 millones de adultos estadounidenses con un nivel de lectura por debajo del nivel de tercer grado. Tienen dificultades para leer cuentos antes de acostarse, leer recetas y completar solicitudes de empleo, entre otras cosas. Desarrollar una buena app podría tener enormes beneficios para mucha gente, lo que también proporcionaría beneficios para el país.
La siguiente historia ficticia te presentará la forma en que se utilizan los datos y las estadísticas para probar teorías y tomar decisiones. El objetivo es que veas que los procesos de pensamiento no son algebraicos y que es necesario desarrollar nuevas formas de pensar para que podamos validar nuestras teorías o tomar decisiones basadas en evidencia.
Historia Premio Alfabetización de Adultos
Imagina formar parte de un equipo compitiendo por el Xprize de Alfabetización de Adultos. Durante las primeras etapas de desarrollo, un objetivo de tu equipo es crear una app que sea atractiva para el usuario para que la use frecuentemente. Probaron su primera versión (Versión 1) de la aplicación en algunos adultos que carecían de alfabetización básica y encontraron que se utilizó un promedio de 6 horas durante el primer mes. Tu equipo decidió que esto no era muy impresionante y que podrías hacerlo mejor, así que desarrollaste una versión completamente nueva del software designado como Versión 2. Cuando llegó el momento de probar el software, los 10 miembros de tu equipo cada uno se lo dieron a 8 personas diferentes con bajas habilidades de alfabetización. Este grupo de 80 individuos que recibieron el software es un pequeño subconjunto, o muestra, de todos aquellos que tienen bajas habilidades de alfabetización. El objetivo fue determinar si la Versión 2 se usa más de un promedio de 6 horas mensuales.
Si bien los datos finalmente se agruparán, tus compañeros de equipo deciden competir entre sí para determinar a quién grupo de 8 le va mejor. Los resultados se muestran en la siguiente tabla. La columna de la derecha es la media (promedio) de los datos en la fila. La media se encuentra sumando los números en la fila y dividiendo esa suma por 8.
| Miembro del equipo | Versión 2 Datos (horas de uso en 1 mes) | Media | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Tú, el lector | 4.4 | 3.8 | 4.4 | 6.7 | 1.1 | 5.7 | 0.8 | 2.5 | 3.675 |
| Betty | 11 | 8.4 | 8.4 | 2.7 | 4.4 | 8.4 | 5.7 | 4.4 | 6.675 |
| Alegría | 1.6 | 2.2 | 12.5 | 5.7 | 2.2 | 6.6 | 0.8 | 0.3 | 3.9875 |
| Kerissa | 16.1 | 11.1 | 8.7 | 9.1 | 1.4 | 9.1 | 1.2 | 14.4 | 8.8875 |
| Cristal | 0 | 2.1 | 0 | 3.2 | 0.2 | 1.8 | 9.1 | 3.3 | 2.4625 |
| Marcin | 2.2 | 6.3 | 1.3 | 8.8 | 0.8 | 2.7 | 0.9 | 0.8 | 2.975 |
| Tisa | 8.8 | 5.8 | 9.7 | 2.8 | 3.2 | 0.9 | 0.1 | 16.1 | 5.925 |
| Tyler | 11 | 0.9 | 11.3 | 6.6 | 0.3 | 5.9 | 1.7 | 1.9 | 4.95 |
| Patrick | 0.9 | 1.8 | 6.3 | 3.1 | 6.1 | 6.3 | 3.2 | 6.7 | 4.3 |
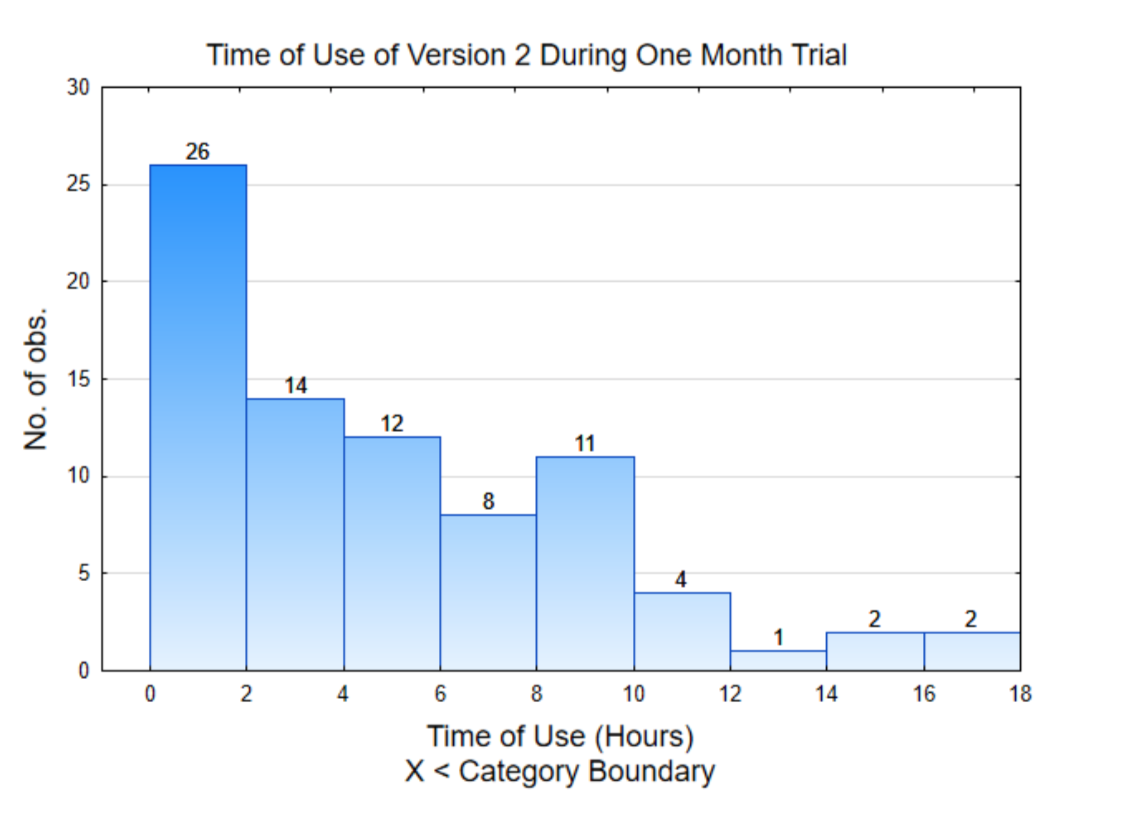
Una forma de darle sentido a los datos es graficarlos. El gráfico de la derecha se llama histograma. Se muestra la distribución de la cantidad de tiempo que el software fue utilizado por cada participante. Para interpretar esta gráfica, observe que la escala en el eje horizontal (x) cuenta por 2. Estos números representan horas de uso. La altura de cada barra muestra cuántos tiempos de uso caen entre los valores x. Por ejemplo, 26 personas usaron la aplicación entre 0 y 2 horas mientras que 2 personas usaron la aplicación entre 16 y 18 horas.
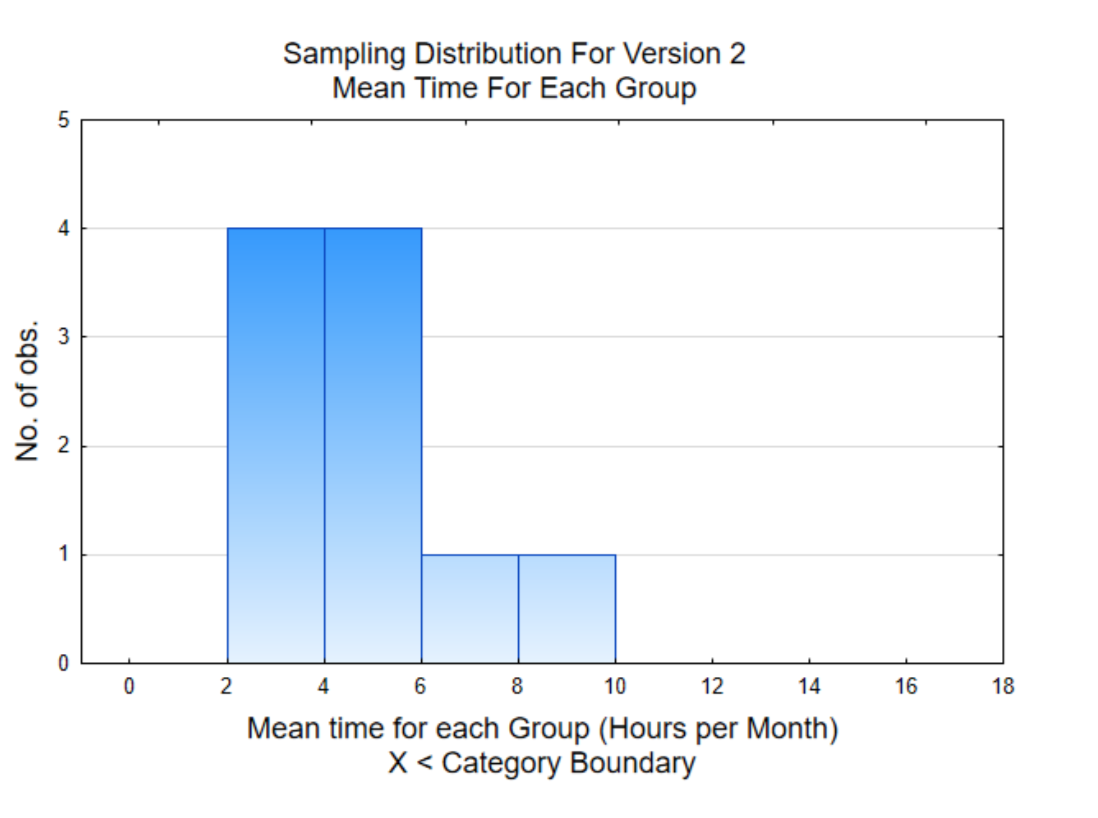
La segunda gráfica es un histograma de la media (promedio) para cada uno de los 10 grupos. Esta es una gráfica de la columna en la tabla que está sombreada. Un histograma de medias se llama distribución de muestreo. La distribución a la derecha muestra que 4 de las medias están entre 2 y 4 horas mientras que solo una media estuvo entre 8 y 10 horas. Observe cómo las medias se agrupan más juntas que los datos originales.
La media general para los 80 valores de datos es de 4.88 horas. Nuestra tarea es utilizar los gráficos y la media general para decidir si se usa la Versión 2 más de lo que se utilizó la Versión 1 (6 horas al mes). ¿Cuál es tu conclusión? Responda a esta pregunta antes de continuar con su lectura.
Sí La versión 2 es mejor que la versión 1 No, la versión 2 no es mejor que la versión 1
¿Cuál de las siguientes tuvo la mayor influencia en tu decisión?
______ 54 de los 80 valores de datos estuvieron por debajo de 6
______ La media de los datos es 4.88, que está por debajo de 6
______ 8 de las 10 medias muestrales están por debajo de 6.
Versión 3
La versión 3 fue un rediseño total del software. Se empleó una estrategia de prueba similar a la de la versión anterior. Cuando recibiste los datos de los 8 usuarios a los que diste el software, encontraste que la duración promedio de uso era de 10.25 horas. En base a tus resultados, ¿sientes que esta versión es mejor que la versión 1?
| Miembro del equipo | Versión 3 Datos (horas de uso en 1 mes) | Media | |||||||
| Tú, el lector | 14 | 13 | 8 | 4 | 8 | 21 | 3 | 11 | 10.25 |
Sí La versión 3 es mejor que la versión 1 No, la versión 3 no es mejor que la versión 1
Su compañera Keer miró sus datos, los cuales se muestran en la siguiente tabla. ¿A qué conclusión llegaría Keer, en base a sus datos?
| Miembro del equipo | Versión 3 Datos (horas de uso en 1 mes) | Media | |||||||
| Keer | 0 | 3 | 2 | 3 | 5 | 4 | 8 | 11 | 4. |
Sí La versión 3 es mejor que la versión 1 No, la versión 3 no es mejor que la versión 1
Si tu interpretación de tus datos y los de Keer son típicos, entonces habrías concluido que la Versión 3 era mejor que la Versión 1 en base a tus datos y la Versión 3 no era mejor basada en los datos de Keer. Esto ilustra cómo diferentes muestras pueden conducir a diferentes conclusiones. Claramente, la conclusión basada en tus datos y la conclusión basada en los datos de Keer no pueden ser ambas correctas. Para ayudar a apreciar quién podría estar en error, veamos todos los datos de las 80 personas que probaron la Versión 3 del software.
| Miembro del equipo | Versión 3 Datos (horas de uso en 1 mes) | Media | |||||||
| Tú, el lector | 14 | 13 | 8 | 4 | 8 | 21 | 3 | 11 | 10.25 |
| Keer | 0 | 3 | 2 | 3 | 5 | 4 | 8 | 11 | 4.5 |
| Betty | 8 | 5 | 5 | 4 | 5 | 0 | 1 | 16 | 5.5 |
| Alegría | 7 | 5 | 8 | 4 | 7 | 13 | 7 | 6 | 7.125 |
| Kerissa | 8 | 6 | 14 | 3 | 11 | 2 | 5 | 8 | 7.125 |
| Cristal | 6 | 7 | 4 | 7 | 6 | 3 | 7 | 5 | 5.625 |
| Marcin | 7 | 7 | 6 | 1 | 2 | 7 | 5 | 5 | 5 |
| Tisa | 3 | 3 | 5 | 4 | 14 | 13 | 3 | 2 | 5.875 |
| Tyler | 0 | 7 | 2 | 7 | 4 | 2 | 5 | 2 | 3.625 |
| Patrick | 8 | 3 | 1 | 14 | 2 | 6 | 7 | 2 | 5.375 |
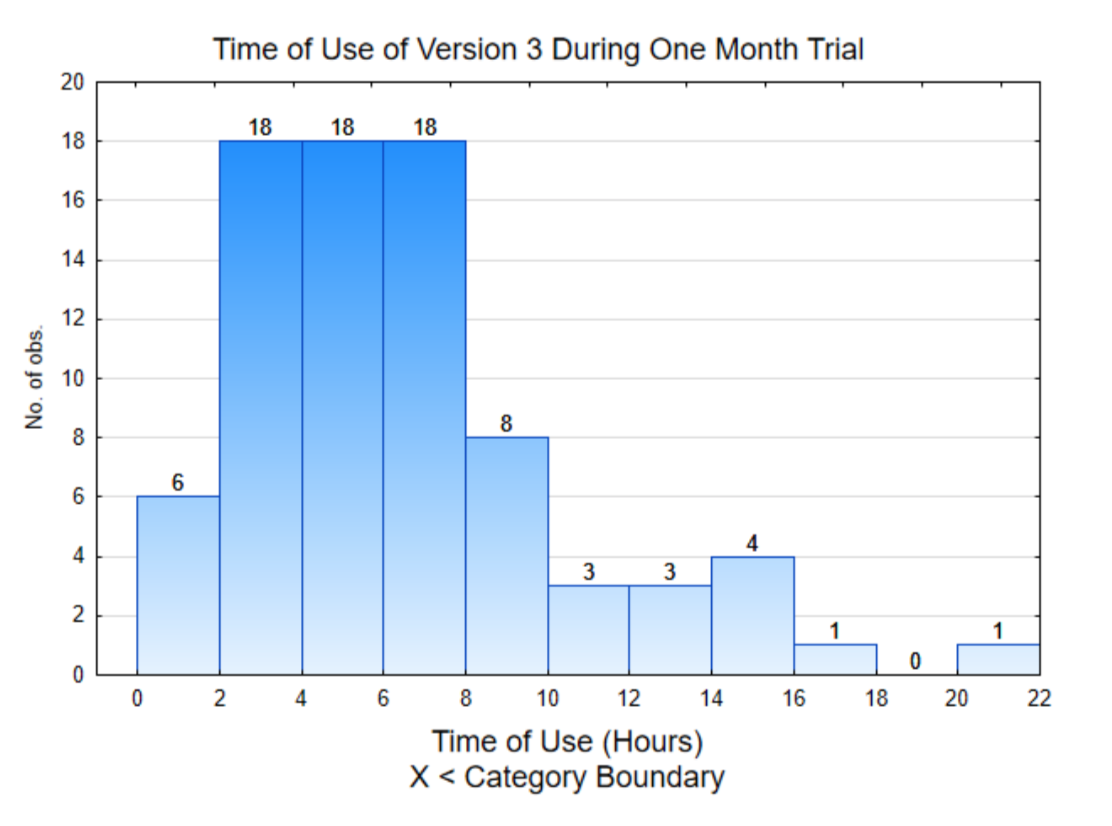
El histograma de la derecha es de los datos de los usuarios individuales. Esto demuestra que aproximadamente la mitad de los datos (42 de 80) están por debajo de 6 y el resto están por encima de 6.
El histograma de la derecha es de la media de los 8 usuarios por cada miembro del equipo. Esta distribución muestral muestra que 7 de las 10 medias muestrales están por debajo de 6.
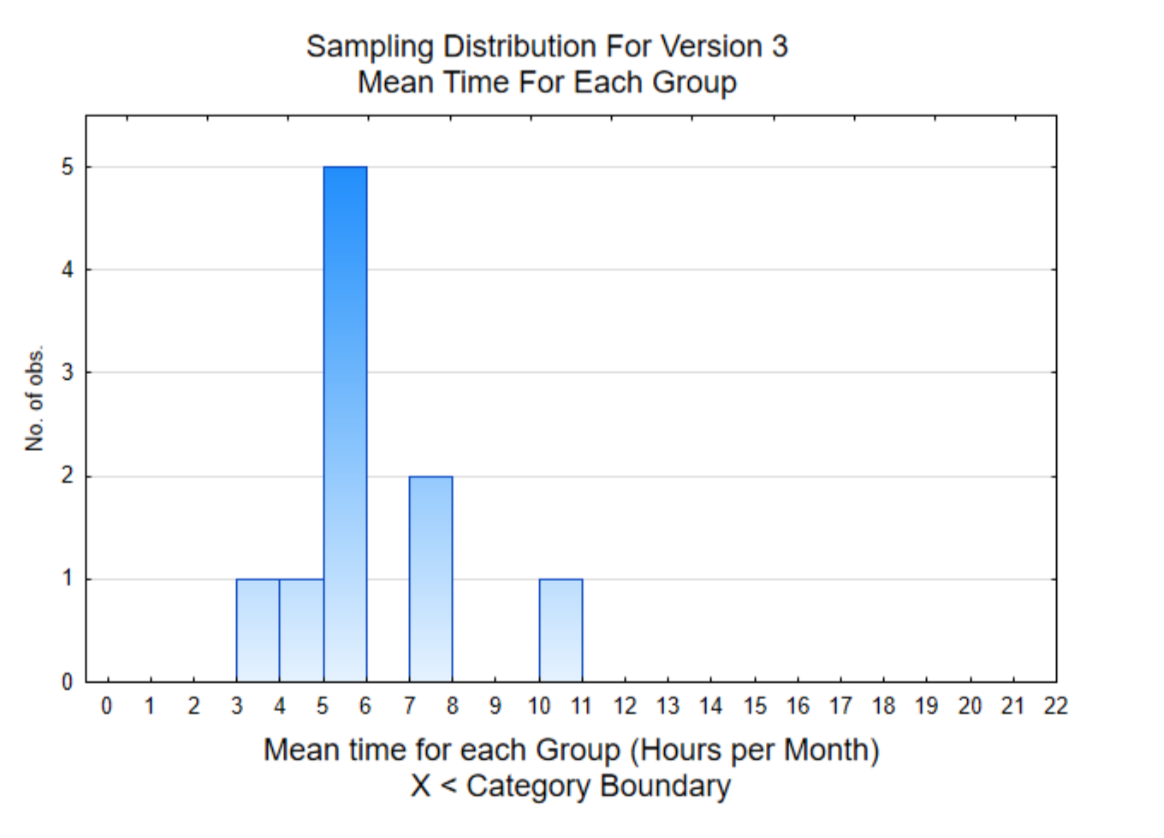
La media de todos los valores de datos individuales es 6.0. En consecuencia, si llegaste a la conclusión de que la Versión 3 era mejor que la Versión 1 porque la media de tus 8 usuarios era de 10.25 horas, habrías llegado a una conclusión equivocada. Habrías sido engañado por datos que fueron seleccionados por pura casualidad.
Ninguna de las primeras 3 versiones tuvo un éxito particular pero su equipo no se desalienta. Ya tienen nuevas ideas y están armando otra versión de su programa de alfabetización.
Versión 4.
Cuando se completa la Versión 4, cada miembro del equipo selecciona aleatoriamente a 8 personas con bajos niveles de alfabetización, tal como se hizo para las versiones anteriores. Los datos que se registran son la cantidad de tiempo que se usa la aplicación durante el mes. Sus datos se muestran a continuación.
| Miembro del equipo | Versión 4 Datos (horas de uso en 1 mes) | Media | ||||||
| Tú, el lector | 60 | 44 | 37 | 62 | 32 | 88 | 32 | 48.375 |
En base a tus resultados, ¿sientes que esta versión es mejor que la versión 1?
Sí La versión 4 es mejor que la versión 1 No, la versión 4 no es mejor que la versión 1
Los resultados de los 80 participantes se muestran en la siguiente tabla.
| Miembro del equipo | Versión 4 Datos (horas de uso en 1 mes) | Media | |||||||
| Tú, el lector | 60 | 44 | 37 | 32 | 62 | 32 | 88 | 32 | 48.375 |
| Keer | 48 | 37 | 24 | 20 | 82 | 76 | 67 | 67 | 52.625 |
| Betty | 88 | 39 | 67 | 24 | 71 | 85 | 81 | 24 | 59.875 |
| Alegría | 23 | 58 | 21 | 88 | 81 | 75 | 84 | 81 | 63.875 |
| Kerissa | 88 | 24 | 58 | 53 | 81 | 57 | 88 | 24 | 59.125 |
| Cristal | 47 | 85 | 767 | 24 | 39 | 67 | 40 | 77 | 56.875 |
| Marcin | 61 | 45 | 75 | 58 | 87 | 51 | 37 | 73 | 60.875 |
| Tisa | 76 | 77 | 58 | 84 | 20 | 55 | 81 | 82 | 66.625 |
| Tyler | 82 | 47 | 48 | 60 | 88 | 21 | 50 | 24 | 52.5 |
| Patrick | 20 | 40 | 52 | 24 | 55 | 33 | 33 | 84 | 42.625 |
El histograma de la derecha es de los datos de los usuarios individuales. Observe que todos estos valores son superiores a 20. 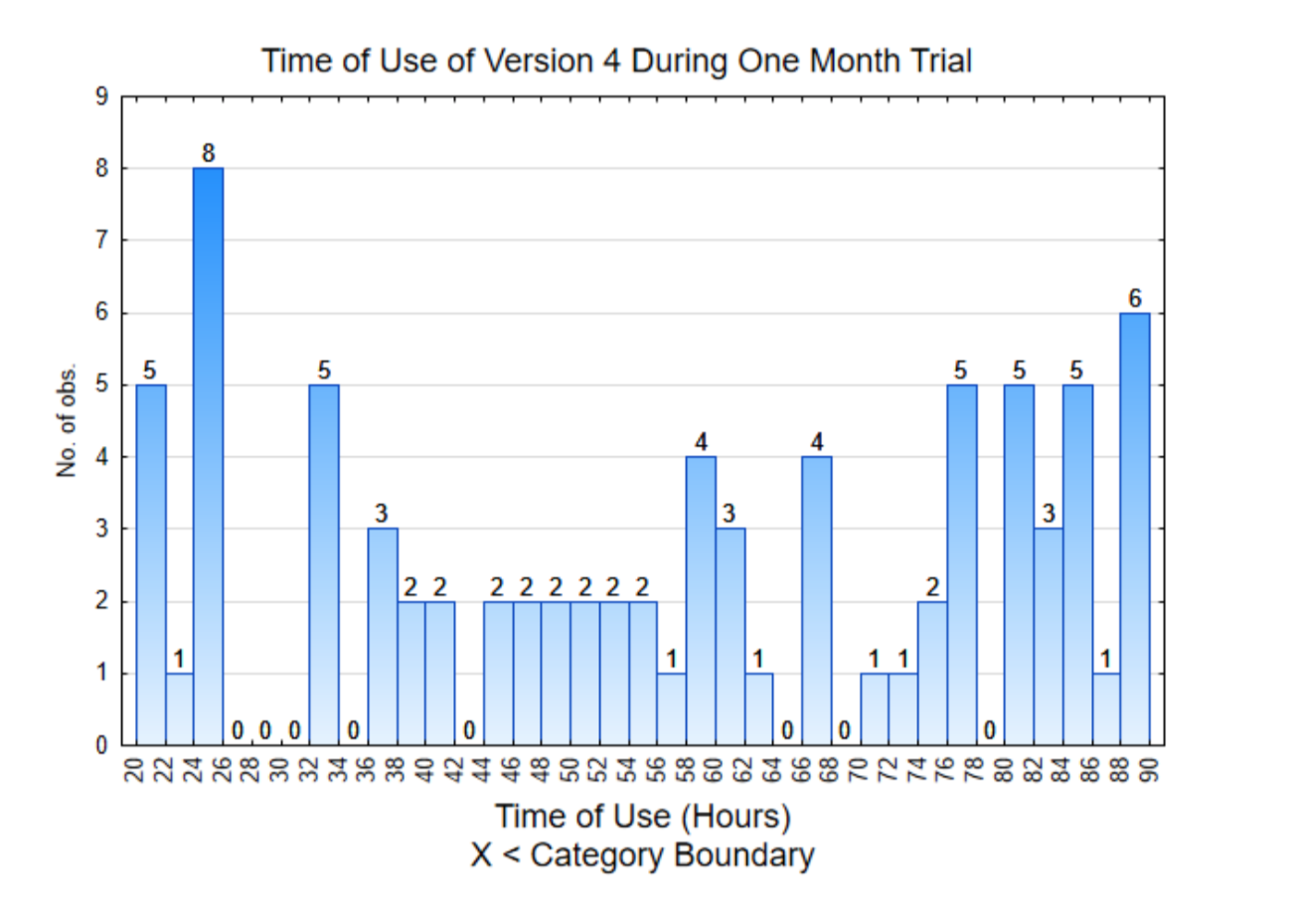
El histograma de la derecha es de la media de los 8 usuarios por cada miembro del equipo. Observe que todas las medias de la muestra son significativamente mayores a 6.
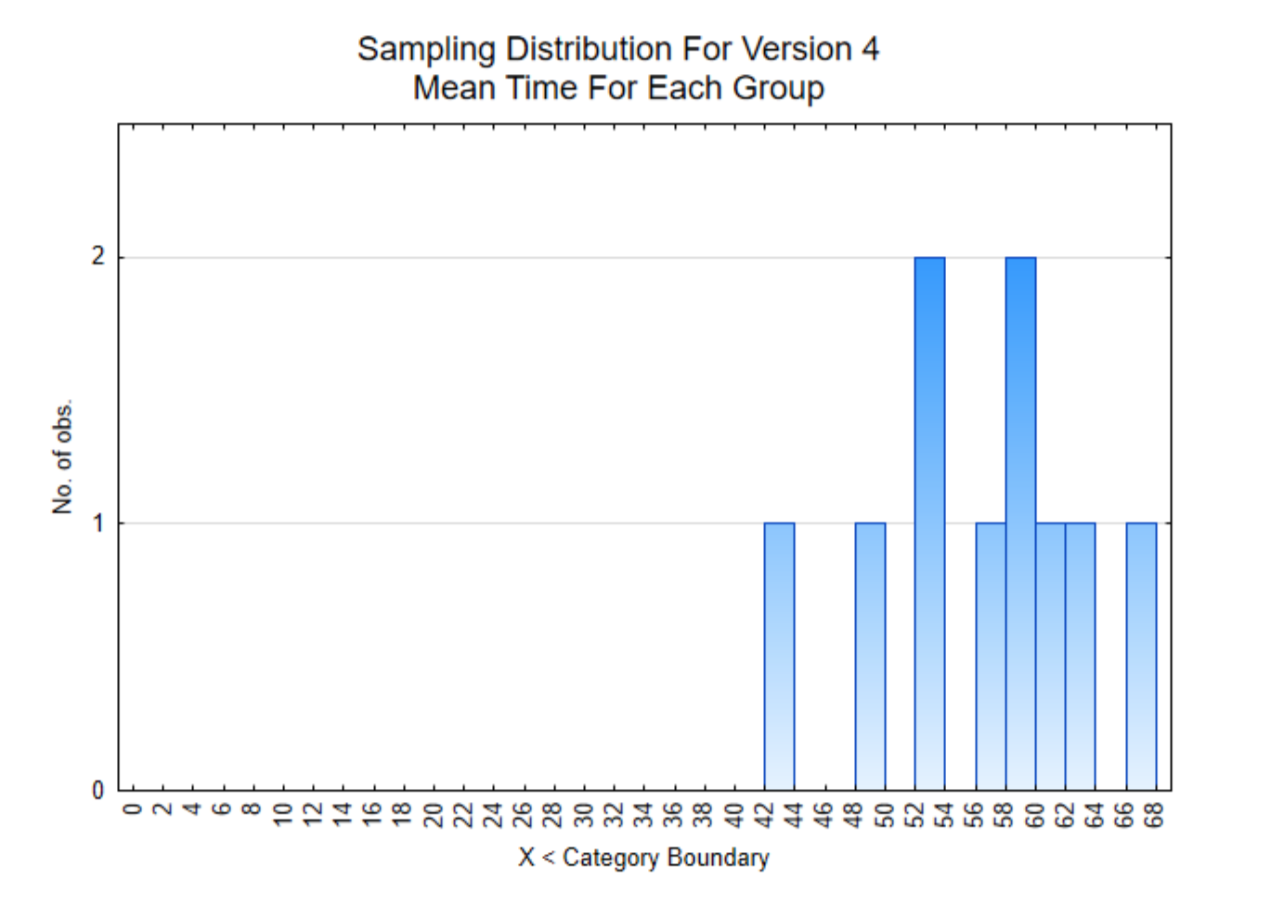
Con base en los resultados de la Versión 4, todos los datos son muy superiores a las 6 horas mensuales. El promedio es de 56.3 horas mensuales que es de casi 2 horas diarias. Esto es significativamente más uso de la aplicación que las primeras versiones y en consecuencia será la aplicación que se utilice en la competencia xPrize.
Tomar decisiones usando estadísticas
Había varios objetivos de la historia que acabas de leer.
- Para darle una apreciación de la variación que puede existir en los datos de muestra.
- Para presentarte un tipo de gráfico de datos llamado histograma, que es una buena manera de observar la distribución de los datos.
- Introducir el concepto de una distribución de muestreo, que es una distribución de medios de una muestra, más que de los datos originales.
- Ilustrar los diversos resultados que pueden ocurrir cuando tratamos de responder preguntas utilizando datos. Estos resultados se resumen a continuación en respuesta a la pregunta de si la nueva versión es mejor que la primera versión.
a. Versión 2: Esto no fue mejor. De hecho, parecía ser peor.
b. Versión 3: Al principio se veía mejor, pero en última instancia era lo mismo.
c. Versión 4: Esto fue mucho mejor.
Debido a que los datos a veces proporcionan claridad sobre una decisión que se debe tomar (Versiones 2 y 4), pero otras veces no es clara (Versión 3), en este capítulo se explicará un proceso de razonamiento estadístico más formal con los detalles que se desarrollarán a lo largo del resto del libro.
Antes de comenzar con este proceso, es necesario tener claro el papel de la estadística para ayudarnos a entender nuestro mundo. Hay dos formas primarias en las que establecemos confianza en nuestro conocimiento del mundo, aportando evidencia analítica o evidencia empírica.
La evidencia analítica hace uso de definiciones o reglas matemáticas. Una prueba matemática es un método analítico para usar hechos establecidos para probar algo nuevo. La evidencia analítica es útil para probar cosas que son deterministas. Determinístico significa que se logrará el mismo resultado cada vez (si no se cometen errores). Álgebra y Cálculo son ejemplos de matemática determinista y pueden ser utilizados para proporcionar evidencia analítica.
En contraste, la evidencia empírica se basa en observaciones. Más específicamente, alguien propondrá una teoría y luego se podrán realizar investigaciones para determinar la validez de esa teoría. La mayoría de las ideas que creemos con confianza han resultado por el rechazo de teorías que anteriormente teníamos y nuestro conocimiento actual consiste en aquellas ideas que no hemos podido rechazar con evidencia empírica. La evidencia empírica se obtiene a través de investigaciones rigurosas. Esto contrasta con la evidencia anecdótica, que también se obtiene a través de la observación, pero no de manera rigurosa. La evidencia anecdótica puede ser engañosa.
El papel de la estadística es evaluar objetivamente la evidencia para que se pueda tomar una decisión sobre si rechazar, o no rechazar una teoría. Es particularmente útil para aquellas situaciones en las que la evidencia es el resultado de una muestra tomada de una población mucho mayor. En contraste con las relaciones deterministas, las poblaciones estocásticas son aquellas en las que hay aleatoriedad, mientras que la evidencia se obtiene mediante muestreo aleatorio, lo que significa que la evidencia que vemos es el resultado del azar.
El método científico que se utiliza en toda la comunidad investigadora para aumentar nuestra comprensión del mundo se basa en proponer y luego probar teorías utilizando métodos empíricos. La estadística juega un papel vital para ayudar a los investigadores a comprender los datos que producen. El método científico contiene los siguientes componentes.
- Haz una pregunta
- Proponer una hipótesis sobre la respuesta a la pregunta
- Investigación de diseño (Capítulo 2)
- Recopilar datos (Capítulo 2)
- Desarrollar una comprensión de los datos mediante gráficos y estadísticas (Capítulo 3)
- Utilizar los datos para determinar si apoyan o contradicen la hipótesis (Capítulos 5,7,8)
- Saque una conclusión.
Antes de explorar las herramientas estadísticas utilizadas en el método científico, es útil comprender los desafíos que enfrentamos con las poblaciones estocásticas y el proceso de razonamiento estadístico que utilizamos para sacar conclusiones.
- Cuando se propone una teoría sobre una población, se basa en cada persona o elemento de la población. Una población es todo el conjunto de personas o cosas de interés.
- Debido a que la población contiene demasiadas personas o elementos de los que obtener información, hacemos una hipótesis sobre cuál sería la información, si pudiéramos obtenerla toda.
- La evidencia se recolecta tomando una muestra de la población.
- La evidencia se utiliza para determinar si la hipótesis debe ser rechazada o no rechazada.
Estos cuatro componentes del proceso de razonamiento estadístico se desarrollarán ahora de manera más completa. El reto es determinar si existe suficiente soporte para la hipótesis, con base en evidencia parcial, cuando se sabe que la evidencia parcial varía, dependiendo de la muestra que se seleccionó. Por analogía, es como tratar de encontrar a la persona adecuada para casarse, obteniendo pruebas parciales de citas o encontrar a la persona adecuada para contratar, obteniendo pruebas parciales de entrevistas.
1. Teorías sobre poblaciones.
Cuando alguien tiene una teoría, esa teoría se aplica a una población que debe definirse claramente. Por ejemplo, una población podría ser todos en el país, o todos los ancianos, o todos en un partido político, o todos los que son atléticos, o todos los que son bilingües, etc. Las poblaciones también pueden ser cualquier parte del mundo natural incluyendo animales, plantas, químicos, agua, etc. Teorías que podrían ser válidas para una población no necesariamente son válidos para otra. Ejemplos de teorías que se aplican a una población incluyen los siguientes.
- El equipo que trabaja en la aplicación de alfabetización teoriza que una versión de su aplicación será utilizada regularmente por toda la población de adultos con bajas habilidades de alfabetización que tengan acceso a ella.
- Una maestra teoriza que su pedagogía docente conducirá al mayor nivel de éxito para toda la población de todos los alumnos que impartirá.
- Una compañía farmacéutica teoriza que un nuevo medicamento será efectivo en el tratamiento de toda la población de personas que padecen una enfermedad que usan el medicamento.
- Un científico de recursos hídricos teoriza que el nivel de contaminación en toda una masa de agua está en un nivel inseguro.
1.5 Datos, Parámetros y Estadísticas
Antes de discutir hipótesis, es necesario hablar de datos, parámetros y estadísticas.
En el nivel más grande, existen dos tipos de datos, categóricos y cuantitativos. Los datos categóricos son datos que se pueden poner en categorías. Los ejemplos incluyen respuestas de sí/no, o categorías como color, religión, nacionalidad, aprobar/fallar, ganar/perder, etc. Los datos cuantitativos son datos que consisten en números resultantes de recuentos o mediciones. Los ejemplos incluyen, estatura, peso, tiempo, cantidad de dinero, número de delitos, frecuencia cardíaca, etc.
Las formas en que entendemos los datos, gráficos y estadísticas, dependen del tipo de datos. Las estadísticas son números utilizados para resumir los datos. Por el momento, hay dos estadísticas que serán importantes, proporciones y medios. Posteriormente en el libro, se introducirán otras estadísticas.
Una proporción es la parte dividida por el conjunto. Es similar al porcentaje, pero no se multiplica por 100. La parte es el número de valores de datos en una categoría. El conjunto es el número de valores de datos que se recolectaron. Así, si se les preguntaba a 800 personas si alguna vez habían visitado un país extranjero y 200 dijeron que sí, entonces la proporción de personas que habían visitado un país extranjero sería:
\(\dfrac{\text{part}}{\text{whole}} = \dfrac{x}{n} = \dfrac{200}{800} = 0.25\)
La parte está representada por la variable x y el todo por la variable n.
Una media, a menudo conocida como promedio, es la suma de los datos cuantitativos dividida por el número de valores de datos. Si nos referimos de nuevo a la aplicación de alfabetización, versión 3, los datos de Marcin fueron:
| Marcin | 7 | 7 | 6 | 1 | 2 | 7 | 5 | 5 | 5 |
La media es\(\dfrac{7+ 7 + 6 + 1 + 2 + 7 + 5 +}{8} = \dfrac{40}{8} = 5\)
Si bien las estadísticas son números que se utilizan para resumir datos de muestra, los parámetros son números que se utilizan para resumir todos los datos de la población. Para encontrar un parámetro, sin embargo, se requiere obtener datos de cada persona o elemento de la población. A esto se le llama censo. Generalmente, es demasiado caro, lleva demasiado tiempo, o simplemente es imposible realizar un censo. Sin embargo, debido a que nuestra teoría es sobre la población, entonces tenemos que distinguir entre parámetros y estadísticas. Para ello, utilizamos diferentes variables.
| Tipo de datos | Resumen | Población | Muestra |
| Categórico | Proporción | p | \(\hat{p}\)(p-sombrero) |
| Cuantitativo | Media | \(\mu\) | \(bar{x}\)(X-bar) |
Para elaborar, cuando los datos son categóricos, la proporción de toda la población se representa con la variable p, mientras que la proporción de la muestra se representa con la variable\(\hat{p}\). Cuando los datos son cuantitativos, la media de toda la población se representa con la letra griega\(\mu\), mientras que la media de la muestra se representa con la variable\(bar{x}\).
En una situación típica, no sabremos ni p ni\(\mu\) y así haríamos una hipótesis sobre ellos. A partir de los datos que recogemos encontraremos\(\hat{p}\) o\(bar{x}\) y los usaremos para determinar si debemos rechazar nuestra hipótesis.
2. Hipótesis
Se escriben hipótesis sobre los parámetros antes de que se recojan los datos (a priori). Las hipótesis se escriben en pares que contienen una hipótesis nula (\(H_0\)) y una hipótesis alternativa (\(H_1\)).
Supongamos que alguien tuviera una teoría de que la proporción de personas que han asistido a un evento deportivo en vivo en el último año fue mayor a 0.2. En tal caso, escribirían sus hipótesis como:
\(H_0\):\(p = 0.2\)
\(H_1\):\(p > 0.2\)
Si alguien tuviera una teoría de que las horas medias de ver eventos deportivos en la televisión eran menos de 15 horas semanales, entonces escribirían sus hipótesis como:
\(H_0\):\(\mu\) = 15
\(H_1\):\(\mu\) < 15
Las reglas que se utilizan para escribir hipótesis son:
- Siempre hay dos hipótesis, la nula y la alternativa.
- Ambas hipótesis son aproximadamente el mismo parámetro.
- La hipótesis nula siempre contiene el signo igual (=).
- La alternativa contiene un signo de desigualdad (<, >, ≠).
- El número será el mismo para ambas hipótesis.
Cuando se utilizan hipótesis para la toma de decisiones, deben seleccionarse de tal manera que si la evidencia sustenta la hipótesis nula, se debe tomar una decisión, mientras que la evidencia que sustente la hipótesis alternativa conduzca a una decisión diferente.
La hipótesis que los investigadores desean es a menudo la hipótesis alternativa. La hipótesis que se pondrá a prueba es la hipótesis nula. Si la hipótesis nula es rechazada por la evidencia, entonces se acepta la hipótesis alternativa. Si la evidencia no conduce a un rechazo de la hipótesis nula, no podemos concluir que el nulo es cierto, solo que no fue rechazado. Utilizaremos el término “apoyado” en este texto. Así, o bien la hipótesis nula es apoyada por los datos o la hipótesis alternativa es apoyada. Estar apoyados por los datos no significa que la hipótesis sea cierta, sino que la decisión que tomemos debe basarse en la hipótesis que se sustenta.
Dos de las situaciones que encontrarás en este texto son cuando hay una teoría sobre la proporción o media para una población o cuando hay una teoría sobre cómo la proporción o media se compara entre dos poblaciones. Estos se resumen en la siguiente tabla.
|
Hipótesis sobre una población |
Notación |
Hipótesis sobre 2 poblaciones |
Notación |
|
La proporción es mayor a 0.2 |
\(H_0\):\(p = 0.2\) |
La proporción de la población A es mayor que la proporción de la población B |
\(H_0\):\(p_A = p_B\) |
|
La proporción es inferior a 0.2 |
\(H_0\):\(p = 0.2\) |
La proporción de la población A es menor que la proporción de la población B |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A < p_B\) |
|
La proporción no es igual a 0.2 |
\(H_0\):\(p = 0.2\) |
La proporción de población A es diferente a la proporción de población B |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A \ne p_B\) |
|
La media es mayor que 15 |
\(H_0\):\(\mu = 15\) |
La media de la población A es mayor que la media de la población B |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A > \mu_B\) |
|
La media es inferior a 15 |
\(H_0\):\(\mu = 15\) \(H_1\):\(\mu < 15\) |
La media de la población A es menor que la media de la población B |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A < \mu_B\) |
|
La media no es igual a 15 |
\(H_0\):\(\mu = 15\) \(H_1\):\(\mu \ne 15\) |
La media de la población A es diferente a la media de la población B |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A \ne \mu_B\) |
3. Usar evidencia para determinar qué hipótesis es más probable que sea correcta.
De la historia de Literacy App, deberías haber visto que a veces la evidencia apoya claramente una conclusión (por ejemplo, la versión 2 es peor que la versión 1), a veces apoya claramente la otra conclusión (la versión 4 es mejor que la versión 1), y a veces es demasiado difícil de decir (versión 3). Antes de discutir una forma más formal de probar hipótesis, desarrollemos cierta intuición sobre las hipótesis y la evidencia.
Supongamos que las hipótesis son
\(H_0\): p = 0.4
\(H_0\): p < 0.4
Si la evidencia de la muestra es\(\hat{p} = 0.45\), ¿apoyaría esta evidencia la nula o alternativa? Decidir antes de continuar.
Las hipótesis contienen un signo igual y un signo menor que pero no un signo mayor que, así que cuando la evidencia es mayor que, ¿qué conclusión se debe sacar? Dado que la proporción muestral no soporta la hipótesis alternativa porque no es inferior a 0.4, entonces concluiremos que 0.45 apoya la hipótesis nula.
Si la evidencia de la muestra es\(\hat{p}\) = 0.12, ¿apoyaría esta evidencia la nula o alternativa? Decidir antes de continuar.
En este caso, 0.12 es considerablemente menor que 0.4, por lo tanto apoya la alternativa.
Si la evidencia de la muestra es\(\hat{p}\) = 0.38, ¿esta evidencia apoyaría la nula o alternativa? Decidir antes de continuar.
Esta es una situación que es más difícil de determinar. Si bien podrías haber decidido que 0.38 es menor que 0.4 y por lo tanto apoya la alternativa, es más probable que apoye la hipótesis nula.
¿Cómo puede ser eso?
En aritmética, 0.38 es siempre menor que 0.4. No obstante, en la estadística, no es necesariamente así. La razón es que la hipótesis se trata de un parámetro, se trata de toda la población. Por otro lado, la evidencia es de la muestra. Diferentes muestras arrojan resultados diferentes. No es apropiada una comparación directa del estadístico (0.38) con el parámetro hipotético (0.4). Más bien, necesitamos una forma diferente de tomar esa determinación. Antes de elaborar el camino diferente, probemos con otro.
Supongamos que las hipótesis son
\(H_0\):\(\mu = 30\)
\(H_1\):\(\mu > 30\)
Si la evidencia de la muestra es\(\bar{x}\) = 80, ¿qué hipótesis se sustenta? Alternativa Null
Si la evidencia de la muestra es\(\bar{x}\) = 26, ¿qué hipótesis se sustenta? Alternativa Null
Si la evidencia de la muestra es\(\bar{x}\) = 32, ¿qué hipótesis se sustenta? Alternativa Null
Si la evidencia es\(\bar{x}\) = 80, se apoyaría la alternativa. Si la evidencia es\(\bar{x}\) = 26, se apoyaría el nulo. Si la evidencia es\(\bar{x}\) = 32, a primera vista, parece apoyar la alternativa, pero está cerca de la hipótesis, por lo que concluiremos que no estamos seguros de cuál apoya.
Puede ser desconcertante para usted no poder sacar una conclusión clara de las pruebas. Después de todo, ¿cómo puede la gente tomar una decisión? Lo que sigue es una explicación de la estrategia de razonamiento estadístico que se utiliza.
Proceso de razonamiento estadístico
El proceso de razonamiento para decidir qué hipótesis sustentan los datos es el mismo para cualquier parámetro (p o μ).
- Supongamos que la hipótesis nula es verdadera.
- Recopilar datos y calcular la estadística.
- Determinar la probabilidad de seleccionar los datos que produjeron la estadística o podrían producir una estadística más extrema, asumiendo que la hipótesis nula es verdadera.
- Si los datos son probables, apoyan la hipótesis nula. Sin embargo, si son poco probables, apoyan la hipótesis alternativa.
Para ilustrar esto, usaremos una pregunta de investigación diferente: “¿Qué proporción de adultos estadounidenses cree que debemos hacer la transición a una sociedad que ya no usa combustibles fósiles (carbón, petróleo, gas natural)? Supongamos que un investigador tiene una teoría de que la proporción de adultos estadounidenses que creen que debemos hacer esta transición es mayor a 0.6. Las hipótesis que se utilizarían para ello son:
\(H_0\): p = 0.6
\(H_1\): p > 0.6
Podríamos visualizar esta situación si usáramos una bolsa de canicas. Dado que el primer paso en el proceso de razonamiento estadístico es asumir que la hipótesis nula es cierta, entonces nuestra bolsa de canicas podría contener 6 canicas verdes que representan a los adultos que quieren dejar de usar combustibles fósiles, y 4 mármoles blancos para representar a quienes quieren seguir usando combustibles fósiles. El muestreo se realizará con reemplazo, lo que significa que después de recoger una canica, se registra el color y la canica se vuelve a colocar en la bolsa.
Si se seleccionan 100 canicas de la bolsa (con reemplazo), ¿espera que exactamente 60 de ellas (60%) sean verdes? ¿Esto sucedería cada vez?
A continuación se muestran los resultados de una simulación por computadora de este proceso de muestreo. La simulación es de 100 canicas seleccionadas, repitiéndose el proceso 20 veces.
| 0.62 | 0.57 | 0.58 | 0.64 | 0.64 | 0.53 | 0.73 | 0.55 | 0.58 | 0.55 |
| 0.61 | 0.66 | 0.6 | 0.54 | 0.54 | 0.5 | 0.62 | 0.55 | 0.61 | 0.61 |
Observe que algunas de las veces, la proporción muestral es mayor que 0.6, algunas de las veces es menor que 0.6 y solo hay una vez en la que realmente igualó 0.6. De esto podemos inferir que aunque la hipótesis nula realmente era cierta, existen proporciones muestrales que podrían hacernos pensar que la alternativa es verdadera (lo que podría llevarnos a cometer un error).
Hay tres ítems en el proceso de razonamiento estadístico que necesitan ser aclarados. El primero es determinar qué valores son probables o improbables que ocurran mientras que el segundo es determinar el punto de división entre probable e improbable. El tercer punto de aclaración es la dirección del extremo.
Valores probables e improbables
Cuando la evidencia se recolecta tomando una muestra aleatoria de la población, la muestra aleatoria que realmente se selecciona es solo una de muchas, muchas, muchas muestras posibles que podrían haberse tomado en su lugar. Cada muestra aleatoria produciría diferentes estadísticas. Si pudieras ver todas las estadísticas, podrías determinar si la muestra que tomaste era probable o improbable. Una gráfica de estadísticas, como proporciones muestrales o medias muestrales, se denomina distribución muestral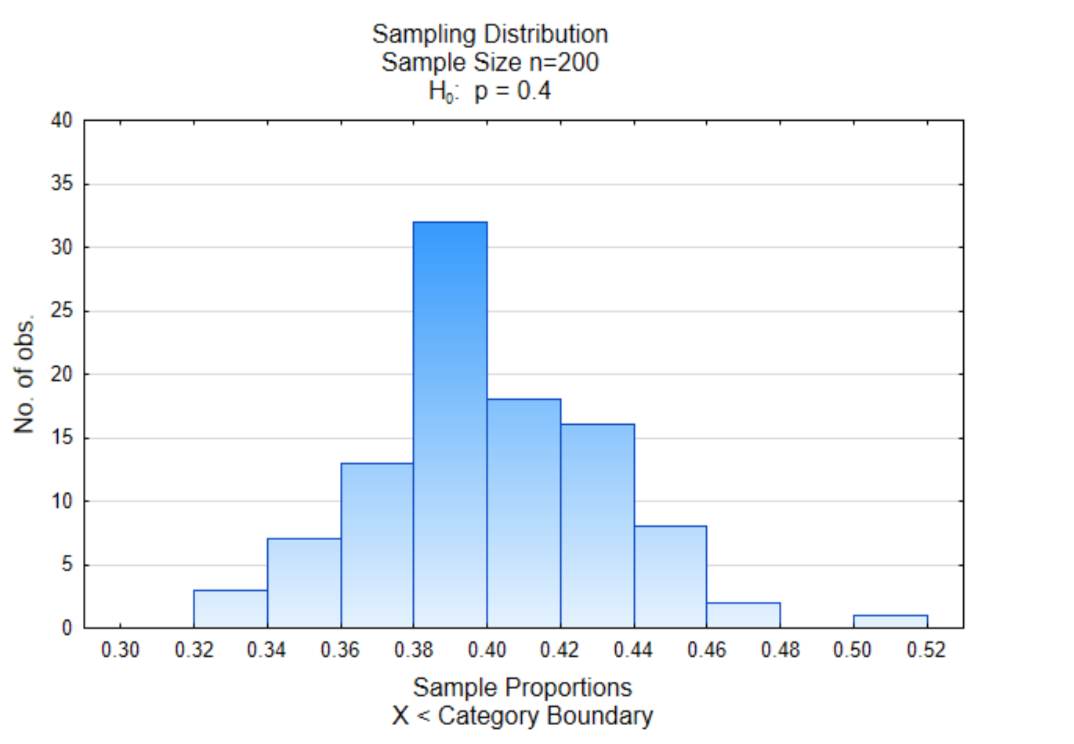 .
.
Si bien no tiene sentido tomar muchas muestras diferentes para encontrar todas las estadísticas posibles, algunas demostraciones de lo que sucede si alguien hace eso pueden darte cierta confianza de que resultados similares también ocurrirían en otras situaciones. Los datos utilizados en las siguientes gráficas se realizaron mediante simulaciones por computadora.
El histograma de la derecha es una distribución muestral de proporciones muestrales. Se seleccionaron 100 muestras diferentes que contenían 200 valores de datos de una población en la que 40% favoreció la sustitución de combustibles fósiles (mármoles verdes). Se encontró la proporción a favor del reemplazo de combustibles fósiles (mármoles verdes) para cada muestra y se graficó. Hay dos cosas que debes notar en la gráfica. La primera es que la mayoría de las proporciones de la muestra se agrupan en el medio y lo segundo es que el medio es aproximadamente 0.40 lo que equivale a la proporción de mármoles verdes en el contenedor.
Eso puede, por supuesto, haber sido una coincidencia. Entonces veamos una muestra diferente. En esta, la población original era 60% de mármoles verdes que representaban a los que estaban a favor de sustituir a los combustibles fósiles. El tamaño de la muestra fue de 500 y el proceso se repitió 100 veces. 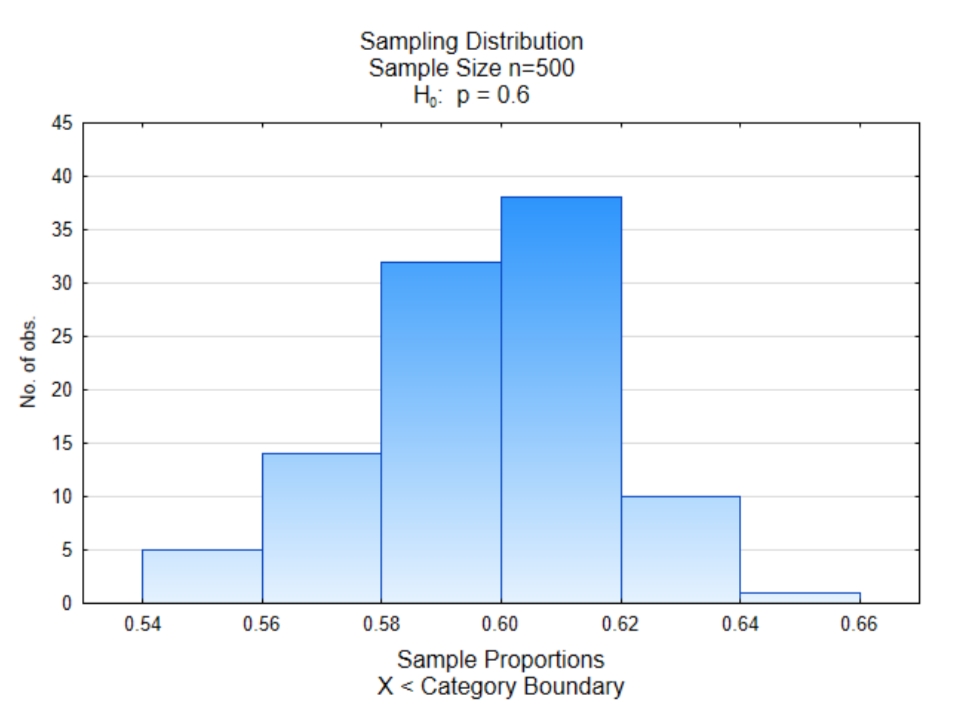
Una vez más vemos la mayoría de las proporciones muestrales agrupadas en el medio y el medio está alrededor del valor de 0.60, que es la proporción de mármoles verdes en la población original.
Veremos un ejemplo más. En este ejemplo, la proporción a favor de la sustitución de combustibles fósiles es de 0.80 mientras que la proporción de los opuestos es de 0.20. El tamaño de la muestra será de 1000 y habrá 100 muestras de ese tamaño. ¿Dónde espera que caiga el centro de esta distribución? 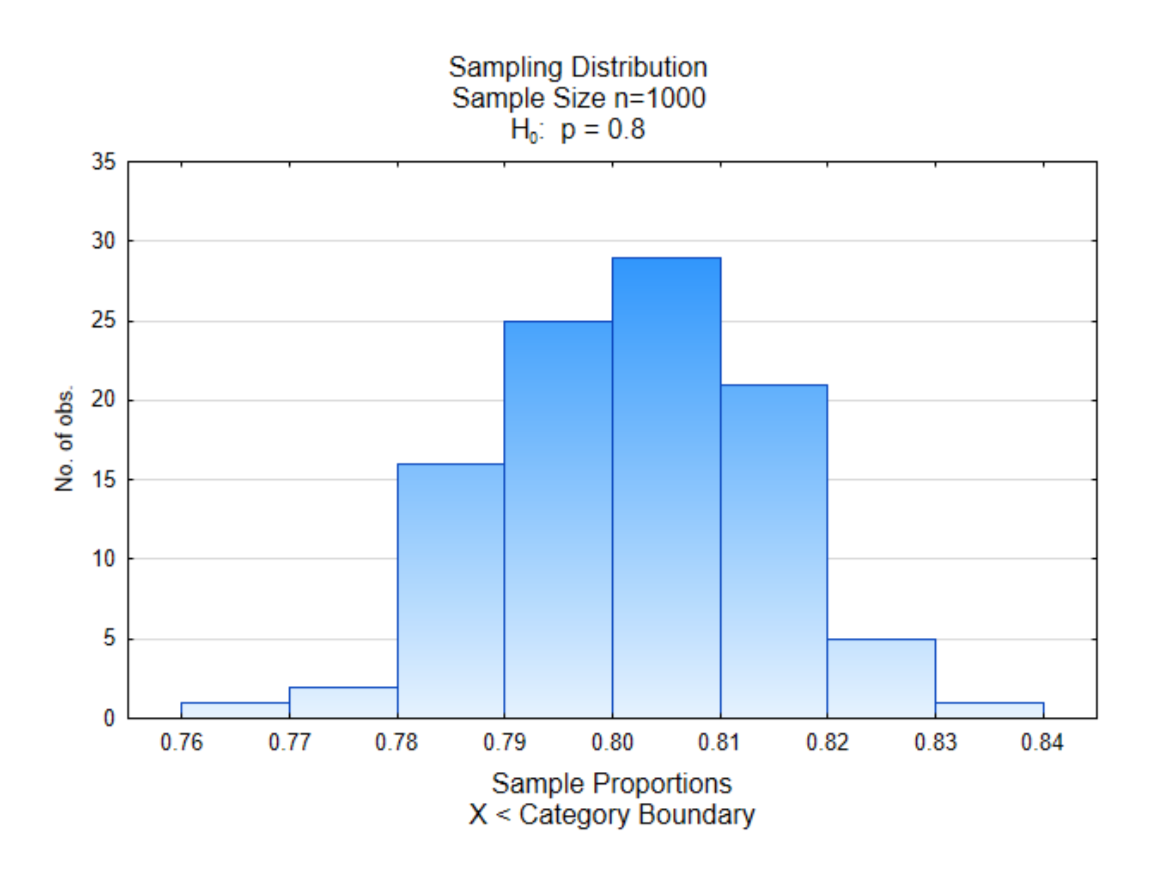
Como puede ver, el centro de esta distribución está cerca de 0.80 con más valores cerca del medio que en los bordes.
Un tema que no se ha abordado es el efecto del tamaño de la muestra. Los tamaños de muestra se representan con la variable n. Estas tres gráficas tenían diferentes tamaños de muestra. La primera muestra tuvo n=200, la segunda tuvo n=500 y la tercera tuvo n=1000. Para ver el efecto de estos diferentes tamaños de muestra, los tres conjuntos de proporciones de muestra se han graficado en el mismo histograma. 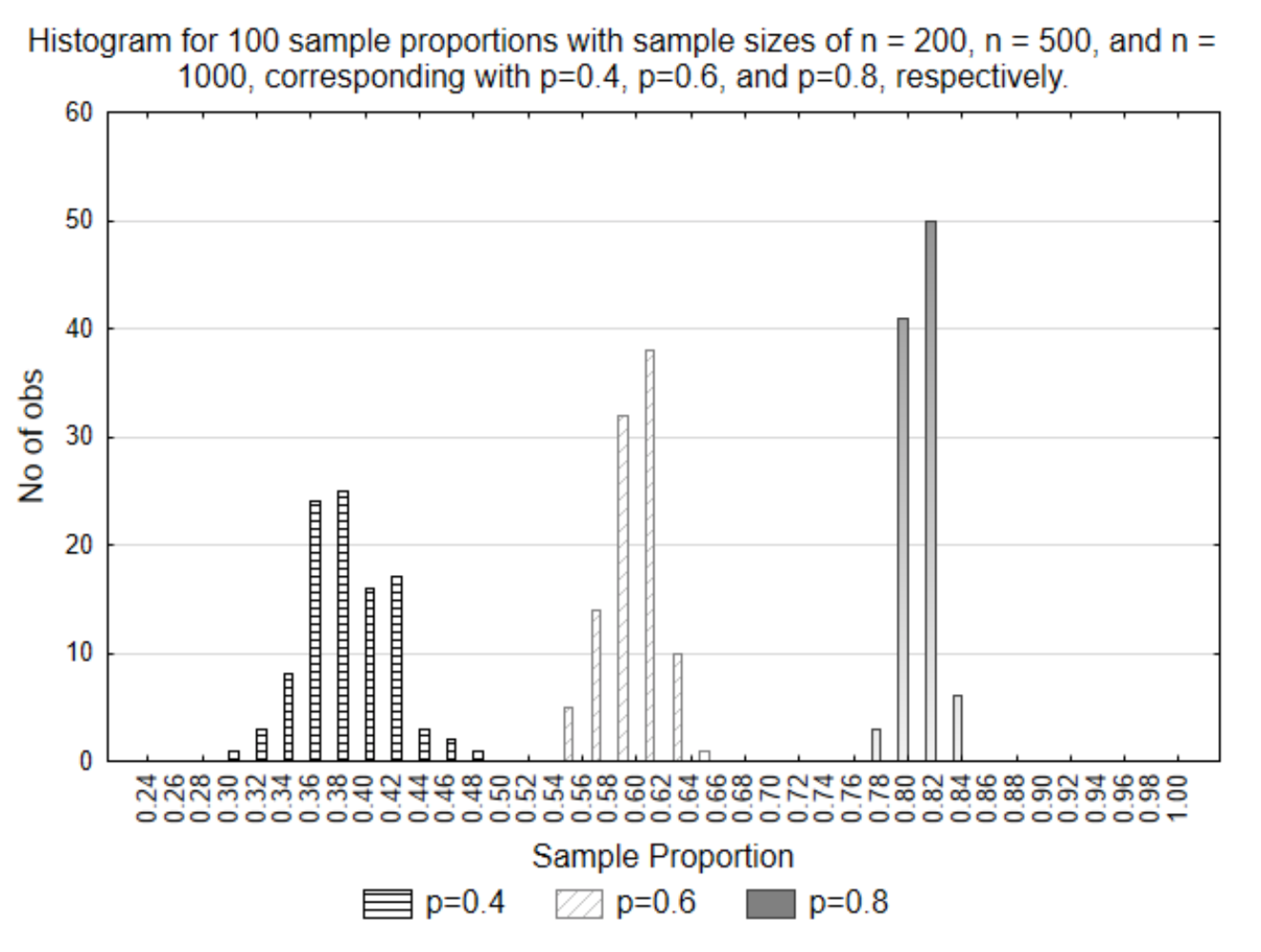
Lo que esta gráfica ilustra es que cuanto menor es el tamaño de la muestra, mayor es la variación que existe en las proporciones de la muestra. Esto es evidente porque están más dispersos. Por el contrario, cuanto mayor es el tamaño de la muestra, menor es la variación que existe. Lo que esto significa es que cuanto mayor sea el tamaño de la muestra, más cerca estará el resultado de la muestra del parámetro. ¿Esto parece razonable? Si hubiera 10 mil personas en una población y obtuviste la opinión de 9,999 de ellas, ¿crees que todas tus posibles proporciones de muestra estarían más cerca del parámetro (proporción poblacional) que si solo preguntaras a 20 personas?
Volveremos a las distribuciones de muestreo en poco tiempo, pero primero necesitamos aprender sobre direcciones de extremos y probabilidad.
Dirección de Extreme
La dirección del extremo es la dirección (izquierda o derecha) en una recta numérica que te haría pensar que la hipótesis alternativa es cierta. Mayor que los símbolos tienen una dirección de extremo a la derecha, menos que los símbolos indican que la dirección es hacia la izquierda y los signos no iguales indican una dirección de dos lados de extremo.
| Notación | Notación | Dirección de Extremo |
| \(H_0\):\(p = 0.2\) \(H_1\):\(p > 0.2\) |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A > p_B\) |
Derecha |
| Izquierda | \(H_0\):\(p_A = p_B\) \(H_1\):\(p_A < p_B\) |
Izquierda |
| \(H_0\):\(p = 0.2\) \(H_1\):\(p \ne 0.2\) |
\(H_0\):\(p_A = p_B\) \(H_1\):\(p_A \ne p_B\) |
Dos caras |
| \(H_0\):\(\mu = 15\) \(H_1\):\(\mu > 15\) |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A > \mu_B\) |
Derecha |
| \(H_0\):\(\mu = 15\) \(H_1\):\(\mu < 15\) |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A < \mu_B\) |
Izquierda |
| \(H_0\):\(\mu = 15\) \(H_1\):\(\mu \ne 15\) |
\(H_0\):\(\mu_A = \mu_B\) \(H_1\):\(\mu_A \ne \mu_B\) |
Dos caras |
Probabilidad
En este momento es necesario tener una breve discusión sobre la probabilidad. Una discusión más detallada ocurrirá en el Capítulo 4. Cuando las teorías se prueban empíricamente mediante muestreo de una población estocástica, entonces la muestra que se obtiene se basa en el azar. Cuando se selecciona una muestra a través de un proceso aleatorio y se calcula la estadística, es posible determinar la probabilidad de obtener esa estadística o estadísticas más extremas si conocemos la distribución muestral.
Por definición, la probabilidad es el número de resultados favorables dividido por el número de resultados posibles.
\[P(A) = \dfrac{Number\ of\ Favorable\ Outcomes}{Number\ of\ Possible\ Outcomes}\]
Esta fórmula supone que todos los resultados son igualmente probables como es teóricamente el caso en un proceso de selección aleatoria. Refleja la proporción de veces que se obtendría un resultado si se realizara un experimento un número muy grande de veces. Debido a que no se puede tener un número negativo de resultados o resultados más exitosos que los posibles, la probabilidad es siempre una fracción o un decimal entre 0 y 1. Esto se muestra genéricamente como\(0 \le P(A) \le 1\) donde P (A) representa la probabilidad del evento A.
Uso de distribuciones de muestreo para probar hipótesis
Recuerde nuestra pregunta de investigación, “¿Qué proporción de adultos estadounidenses cree que debemos hacer la transición a una sociedad que ya no usa combustibles fósiles (carbón, petróleo, gas natural)? La teoría de los investigadores es que la proporción de adultos estadounidenses que creen que debemos hacer esta transición es mayor a 0.6. Las hipótesis que se utilizarían para ello son:
\(H_0 : p = 0.6\)
\(H_1 : p > 0.6\)
Para probar esta hipótesis, necesitamos dos cosas. En primer lugar, necesitamos la distribución muestral para la hipótesis nula, ya que asumiremos que eso es cierto, como se afirma primero en la lista para el proceso de razonamiento utilizado para probar una hipótesis. Lo segundo que necesitamos son los datos. Debido a que esto es instructivo, en este punto, se proporcionarán varias proporciones de muestra para que puedas comparar y contrastar los resultados.
Se ha realizado un pequeño cambio en la distribución muestral que se mostró previamente. En la parte superior de cada barra hay una proporción. En el eje x también hay proporciones. La diferencia entre estas proporciones es que las del eje x indican las proporciones de muestra mientras que las proporciones en la parte superior de las barras indican la proporción de proporciones de muestra que estaban entre los dos valores límite. Así, de 100 proporciones de muestra, 0.38 (o 38%) de ellas estuvieron entre 0.60 y 0.62. Las proporciones en la parte superior de las barras también se pueden interpretar como probabilidades.
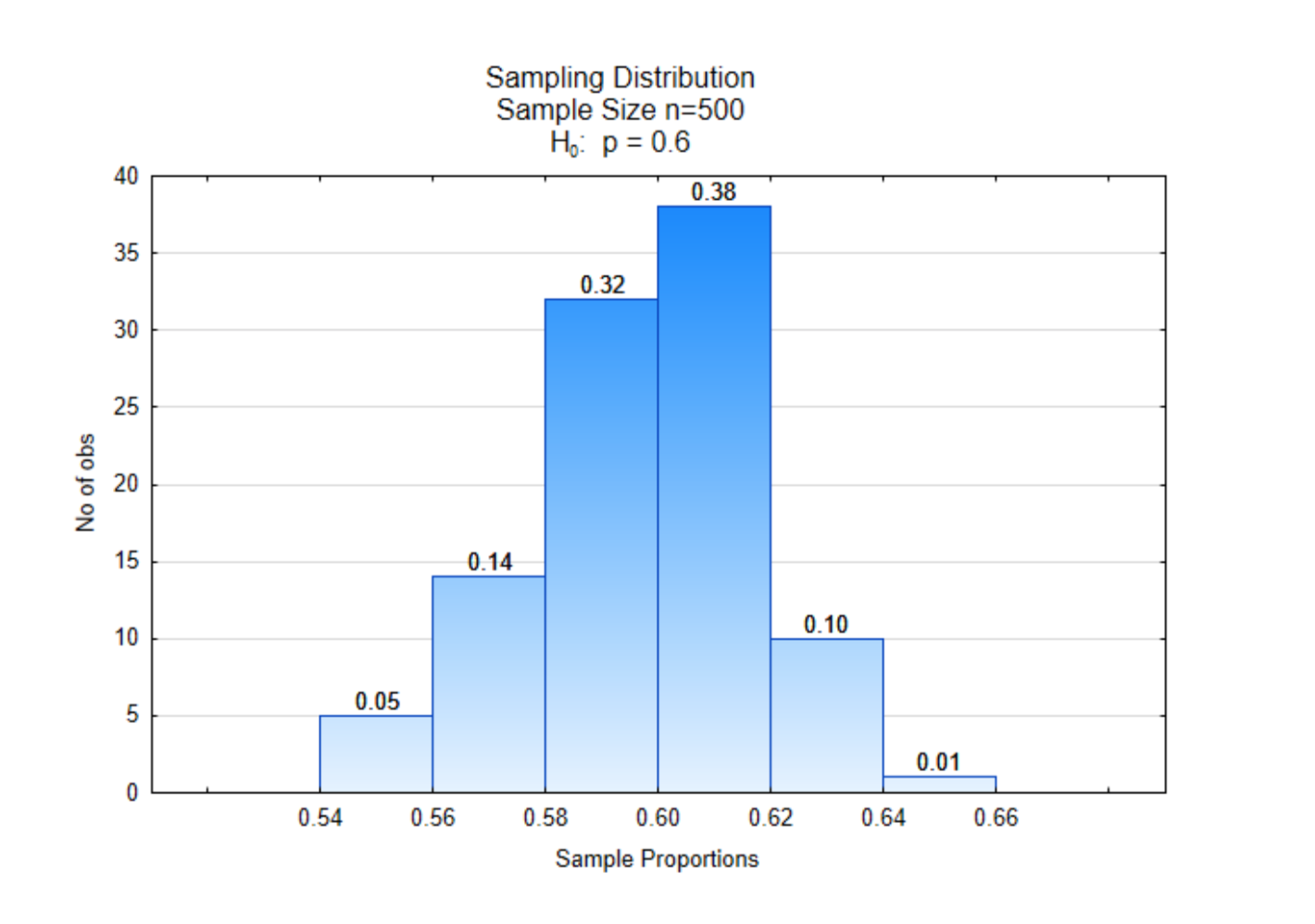
Es con esta distribución de muestreo a partir de las hipótesis nulas que podemos encontrar la probabilidad, o probabilidad de obtener nuestros datos, o datos más extremos. Llamaremos a esta probabilidad un valor p.
Como recordatorio, para la hipótesis que estamos probando, la dirección del extremo es hacia la derecha.
Supongamos que la proporción muestral que obtuvimos para nuestros datos fue\(\hat{p}\) = 0.64. ¿Cuál es la probabilidad de que hubiéramos obtenido esa proporción muestral o más extrema de esta distribución? Esa probabilidad es 0.01, consecuentemente el valor p es 0.01. Este número se encuentra en la parte superior de la barra situada más a la derecha.
Supongamos que la proporción muestral que obtuvimos de nuestros datos fue\(\hat{p}\) = 0.62. ¿Cuál es la probabilidad de que hubiéramos obtenido esa proporción muestral de esta distribución? Esa probabilidad es de 0.11. Esto se calculó sumando las proporciones en la parte superior de las dos barras más a la derecha. El valor p es 0.11.
Lo intentas. Supongamos que la proporción muestral que obtuvimos de nuestros datos fue\(\hat{p}\) = 0.60. ¿Cuál es la probabilidad de que hubiéramos obtenido esa proporción muestral de esta distribución?
Ahora, supongamos que la proporción muestral que obtuvimos de nuestros datos fue\(\hat{p}\) = 0.68. ¿Cuál es la probabilidad de que hubiéramos obtenido esa proporción muestral de esta distribución? En este caso, no hay evidencia de ninguna proporción muestral igual a 0.68 o superior, por lo que consecuentemente la probabilidad, o valor p sería 0.
Probando la hipótesis
Ahora intentaremos determinar qué hipótesis se sustenta en los datos. Utilizaremos la distribución p=0.8 para representar la hipótesis alternativa. Tanto las distribuciones nulas como las alternativas se muestran en la misma gráfica.
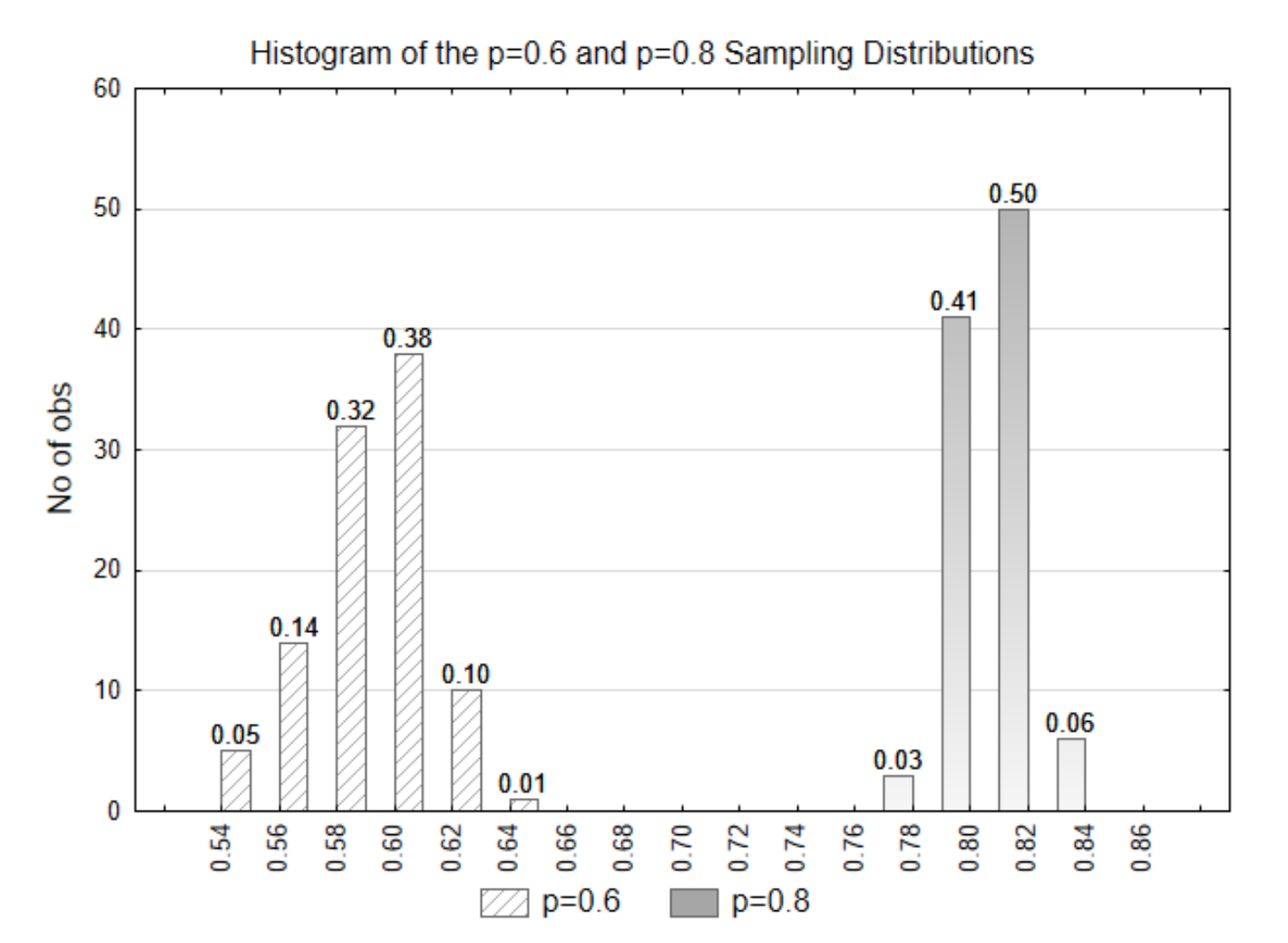
Si los datos que se seleccionan tenían una estadística de\(\hat{p}\) = 0.58, ¿cuál es el valor p? ¿De cuál de las dos distribuciones crees que provienen los datos? ¿Qué hipótesis se apoya?
El valor p es 0.81 (0.32+0.38+0.10+0.01). Estos datos provienen de la distribución nula (p=0.6). Esta evidencia apoya la hipótesis nula.
Si los datos que se seleccionaron fueron\(\hat{p}\) = 0.78, ¿cuál es el valor p? ¿De cuál de las dos distribuciones crees que provienen los datos? ¿Qué hipótesis se apoya?
El valor p es 0 porque no hay valores en la distribución p=0.6 que sean 0.78 o superiores. Los datos provienen de la distribución alternativa (p=0.8). Se sustenta la hipótesis alternativa.
En los ejemplos anteriores, existe una clara distinción entre las distribuciones nulas y alternativas. En el siguiente ejemplo, la distinción no es tan clara. La distribución alternativa se representará con una proporción de 0.65
. 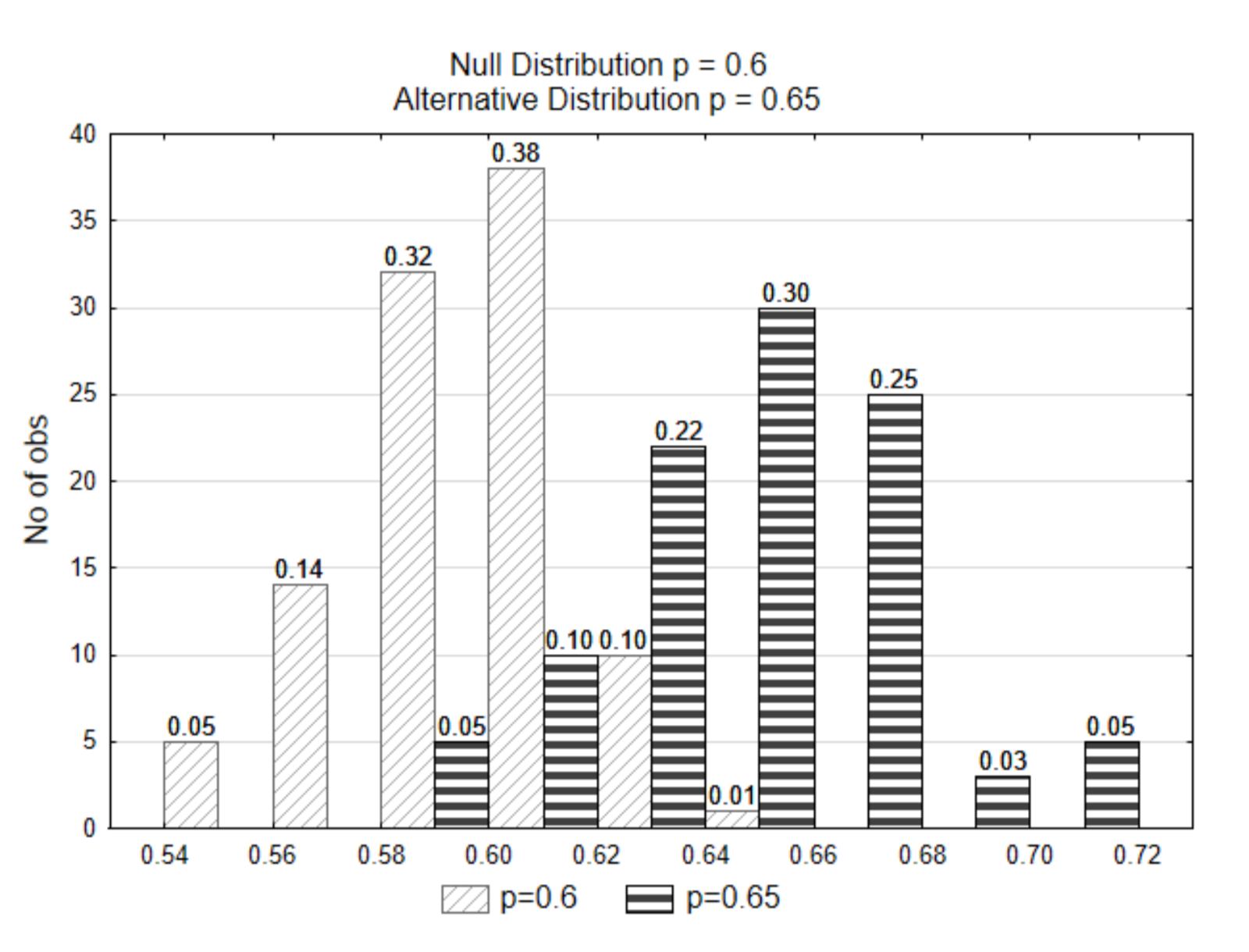
Si los datos que se seleccionan fueron\(\hat{p}\) = 0.62, ¿de cuál de las dos distribuciones cree que provienen los datos? ¿Qué hipótesis se apoya?
Observe que en este caso, debido a que las distribuciones se superponen, una proporción muestral de 0.62 o más extrema podría haber provenido de cualquiera de las dos distribuciones. No está claro de cuál vino. Debido a esta falta de claridad, posiblemente podríamos cometer un error. Podríamos pensar que vino de la distribución nula mientras que realmente vino de la distribución alternativa. O tal vez pensamos que provenía de la distribución alternativa, pero realmente vino de la distribución nula. ¿Cómo decidimos???
Antes de explicar la forma en que decidimos, necesitamos discutir los errores, ya que son parte del proceso de toma de decisiones.
Hay dos tipos de errores que podemos cometer como resultado del proceso de muestreo. Se les conoce como errores de muestreo. Estos errores se denominan errores Tipo I y Tipo II. Un error tipo I ocurre cuando pensamos que los datos apoyan la hipótesis alternativa pero en realidad, la hipótesis nula es correcta. Un error tipo II ocurre cuando pensamos que los datos apoyan la hipótesis nula, pero en realidad la hipótesis alternativa es correcta. En todos los casos de hipótesis de prueba, existe la posibilidad de hacer un error tipo I o tipo II.
La probabilidad de cometer errores de Tipo I o Tipo II es importante en el proceso de toma de decisiones. Representamos la probabilidad de cometer un error Tipo I con la letra griega alfa, \(\alpha\). También se le llama el nivel de significación. La probabilidad de cometer un error Tipo II se representa con la letra griega Beta,\(\beta\). La probabilidad de que los datos respalden la hipótesis alternativa, cuando la alternativa es verdadera, se llama poder. El poder no es un error. Los errores se resumen en la siguiente tabla.
| La verdadera hipótesis | |||
| \(H_0\)Es Cierto | \(H_1\)Es Cierto | ||
| Las pruebas en las que se basa la decisión | Los soportes de datos\(H_0\) | Sin error | Probabilidad de error tipo II:\(\beta\) |
| Los soportes de datos\(H_1\) | Probabilidad de error tipo I:\(\alpha\) | Probabilidad sin error: Potencia | |
Aquí se reproduce el proceso de razonamiento para decidir qué hipótesis sustentan los datos.
- Supongamos que la hipótesis nula es verdadera.
- Recopilar datos y calcular la estadística.
- Determinar la probabilidad de seleccionar los datos que produjeron la estadística o podrían producir una estadística más extrema, asumiendo que la hipótesis nula es verdadera. Esto se llama el valor p.
- Si los datos son probables, apoyan la hipótesis nula. Sin embargo, si son poco probables, apoyan la hipótesis alternativa.
La determinación de si los datos son probables o no se basa en una comparación entre el valor p- y α. Tanto los valores alfa como los valores p son probabilidades. Siempre deben ser valores entre 0 y 1, inclusive. Si el valor p- es menor o igual a α, los datos apoyan la hipótesis alternativa . Si el valor p es mayor que α, los datos soportan la hipótesis nula. Cuando los datos apoyan la hipótesis alternativa, se dice que los datos son significativos. Cuando los datos apoyan la hipótesis nula, los datos no son significativos. Vuelva a leer este párrafo al menos 3 veces ya que define la regla de toma de decisiones utilizada a lo largo de las estadísticas y es fundamental entenderlo.
Debido a que algunos valores apoyan claramente la hipótesis nula, otros apoyan claramente la hipótesis alternativa pero algunos tampoco lo apoyan claramente, entonces se tiene que tomar una decisión, antes de que se recojan datos (a priori), en cuanto a la probabilidad de cometer un error tipo I que sea aceptable al investigador. Los valores más comunes para α son 0.05, 0.01 y 0.10. No hay una razón específica para estas elecciones pero hay una considerable precedencia histórica para ellas y serán utilizadas rutinariamente en este libro. La elección de un nivel de significancia debe basarse en varios factores.
- Si la potencia de la prueba es baja debido a tamaños de muestra pequeños o diseño experimental débil, se debe usar un mayor nivel de significancia.
- Tenga en cuenta el objetivo último de la investigación — “entender qué hipótesis sobre el universo son correctas. En última instancia estas son decisiones de sí y no”. (Scheiner, Samuel M., y Jessica Gurevitch. Diseño y Análisis de Experimentos Ecológicos. Oxford [etc.: Oxford UP, 2001. Imprimir.) Las pruebas estadísticas deben conducir a uno de los tres resultados. Un resultado es que la hipótesis es casi con certeza correcta. El segundo resultado es que la hipótesis es casi con certeza incorrecta. El tercer resultado es que se justifica una mayor investigación. Los valores P- dentro del intervalo (0.01,0.10) pueden garantizar una investigación continuada, aunque estos valores son tan arbitrarios como los niveles de significación comúnmente utilizados.
- Si estamos intentando construir una teoría, deberíamos usar valores más liberales (superiores) de α, mientras que si estamos intentando validar una teoría, deberíamos usar valores más conservadores (inferiores) de\(\alpha\).
Demostración de una prueba de hipótesis elemental
Ahora, tienes todas las partes para decidir qué hipótesis se sustenta en la evidencia (los datos). El problema será replanteado aquí.
\(H_0 : p = 0.6\)
\(H_1 : p > 0.6\)
\(\alpha = 0.01\)
Se dibujó una línea vertical en la gráfica de manera que una proporción de sólo 0.01 estaba a la derecha de la línea en la distribución nula. A esto se le llama línea de decisión porque es la línea la que determina cómo decidiremos si la estadística soporta la hipótesis nula o alternativa. El número en la parte inferior de la línea de decisión se llama el valor crítico.
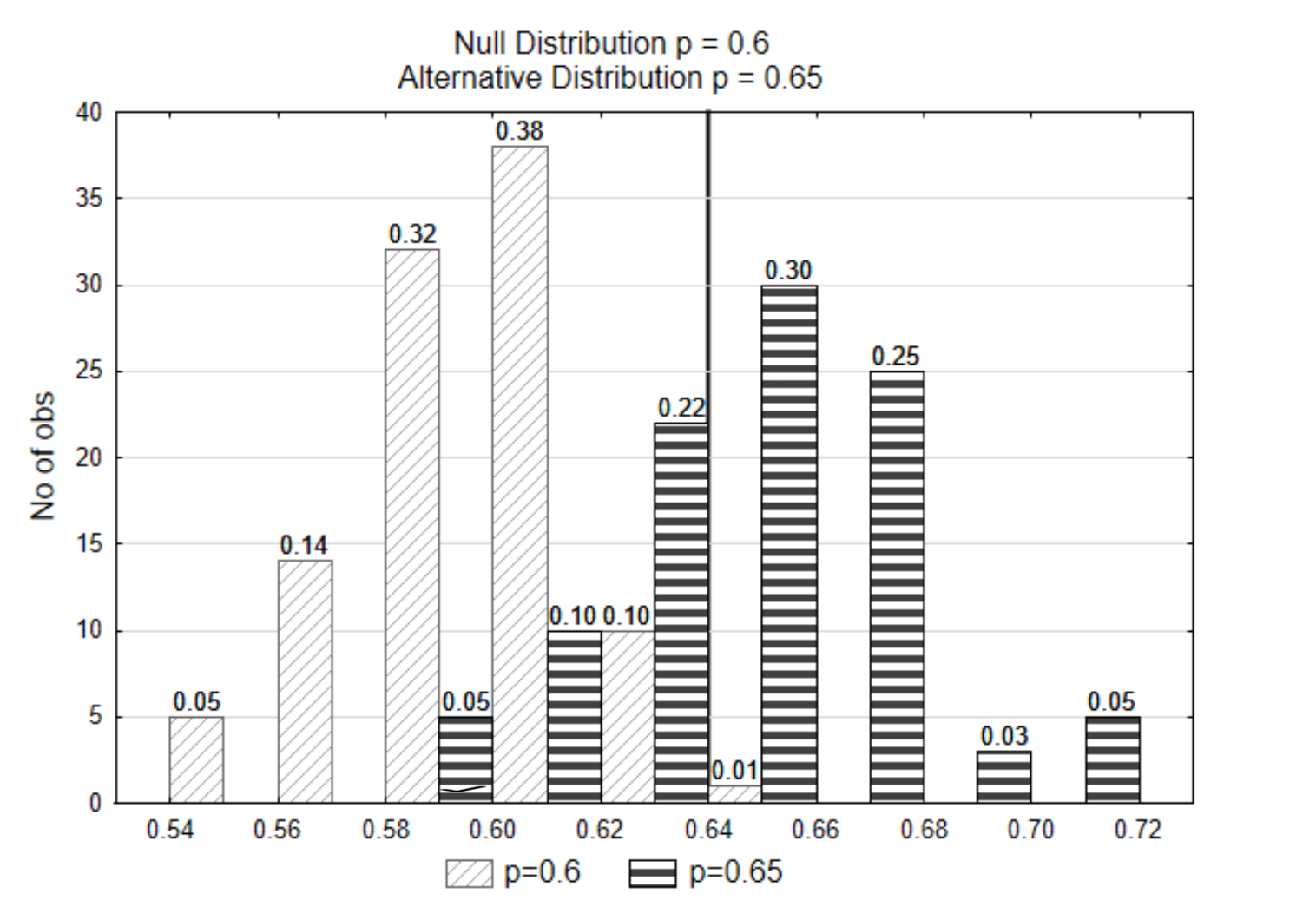
Si los datos que se seleccionan fueron\(\hat{p}\) = 0.62, ¿de cuál de las dos distribuciones cree que provienen los datos? ¿Qué hipótesis se apoya?
Para responder a estas preguntas, primero encuentra el valor p. El valor p es 0.11 (0.10 + 0.01).
A continuación, compare el valor p con\(\alpha\). Desde 0.11 > 0.01, esta evidencia apoya la hipótesis nula.
Debido a que mostrar ambas distribuciones en una misma gráfica puede hacer que la gráfica sea un poco difícil de leer, esta gráfica se dividirá en dos gráficas. La línea de decisión se muestra con el mismo valor crítico en ambas gráficas (0.64). El nivel de significancia, α, se muestra en la distribución nula. Señala en la dirección del extremo. β y la potencia se muestran en la distribución alternativa. La potencia está en el mismo lado de la distribución que la dirección del extremo mientras que β está en el lado opuesto. El valor p también se muestra en la distribución nula, apuntando en la dirección del extremo.
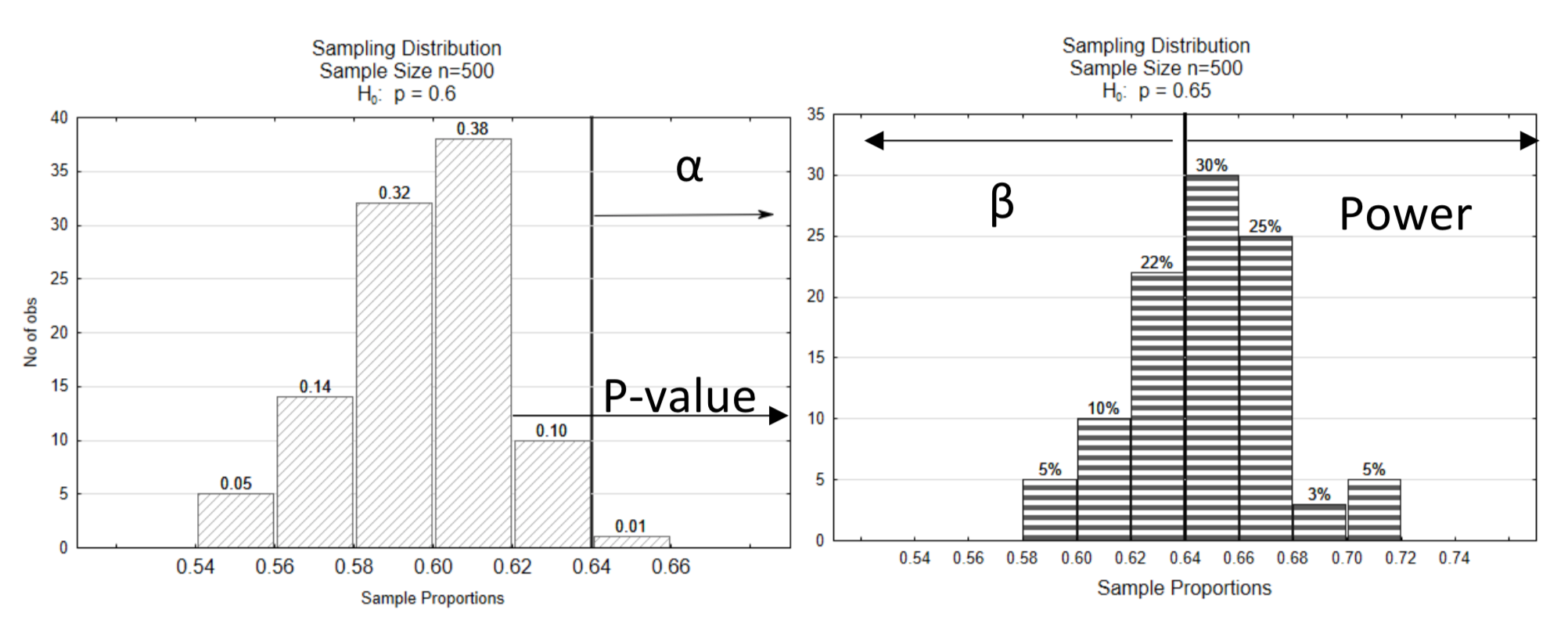
Otro ejemplo se demostrará a continuación.
Pregunta: ¿Cuál es la proporción de personas que han visitado un país diferente?
Teoría: La proporción es menor a 0.40
Hipótesis:\(H_0: p = 0.40\)
\(H_1: p < 0.40\)
\(\alpha = 0.04\)
La distribución de la izquierda es la distribución nula, es decir, es la distribución que se obtuvo por muestreo de una población en la que la proporción de personas que han visitado un país diferente es realmente 0.40. La distribución a la derecha representa la hipótesis alternativa.
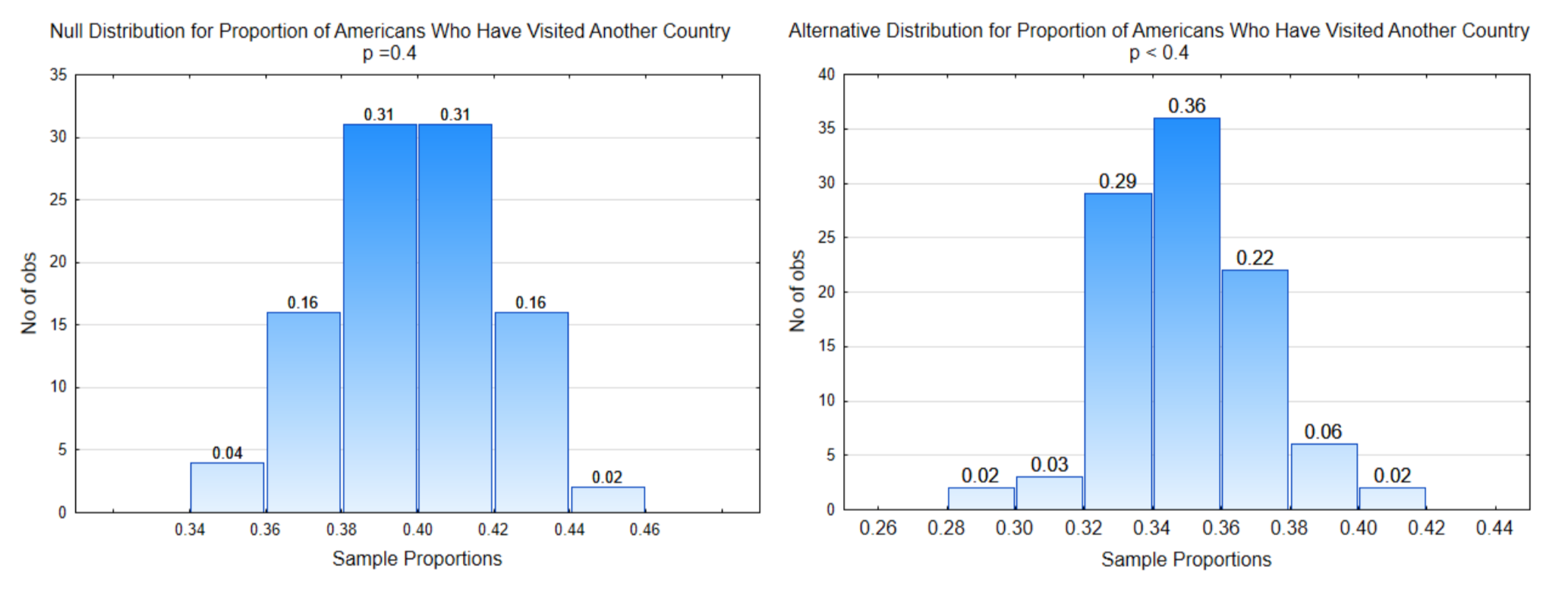
El objetivo es identificar la porción de cada gráfica asociada a α, β y potencia. Una vez proporcionados los datos, también podrás mostrar la parte de la gráfica que indica el valor p.
El proceso de razonamiento para etiquetar las distribuciones es el siguiente.
1. Determinar la dirección del extremo. Esto se hace observando el signo de desigualdad en la hipótesis alternativa. Si el signo es <, entonces la dirección del extremo es hacia la izquierda. Si el signo es >, entonces la dirección del extremo es hacia la derecha. Si el signo es\(\ne\), entonces la dirección del extremo es hacia la izquierda y la derecha, lo que se llama bilateral. Observe que el signo de desigualdad apunta hacia la dirección del extremo. Para que estos conceptos sean un poco más fáciles a medida que los estés aprendiendo, no haremos hipótesis alternativas bilaterales hasta más adelante en el texto.
En este problema la dirección del extremo es hacia la izquierda porque proporciones muestrales más pequeñas apoyan la hipótesis alternativa.
2. Dibuja la línea de Decisión. La dirección del extremo junto con α se utilizan para determinar la ubicación de la línea de decisión. Alfa es la probabilidad de cometer un error Tipo I. Un error Tipo I solo puede ocurrir si la hipótesis nula es verdadera, por lo tanto, siempre colocamos alfa en la distribución nula. Comenzando por el lado de la dirección de extremo, sumar las proporciones en la parte superior de las barras hasta que sean iguales a alfa. Dibuja la línea de decisión entre barras separando aquellas que podrían llevar a un error Tipo I del resto de la distribución.
Observe el valor del eje x en la parte inferior de la línea de decisión. Este valor se llama el valor crítico. Identificar el valor crítico en la distribución alternativa y colocar otra línea de decisión allí.
En este problema, la dirección del extremo es hacia la izquierda y\(\alpha\) = 4% (0.04) por lo que la línea de decisión se coloca de manera que la proporción de proporciones muestrales a la izquierda sea de 0.04. El valor crítico es 0.36 por lo que la otra línea de decisión se coloca en 0.36 en la distribución alternativa.
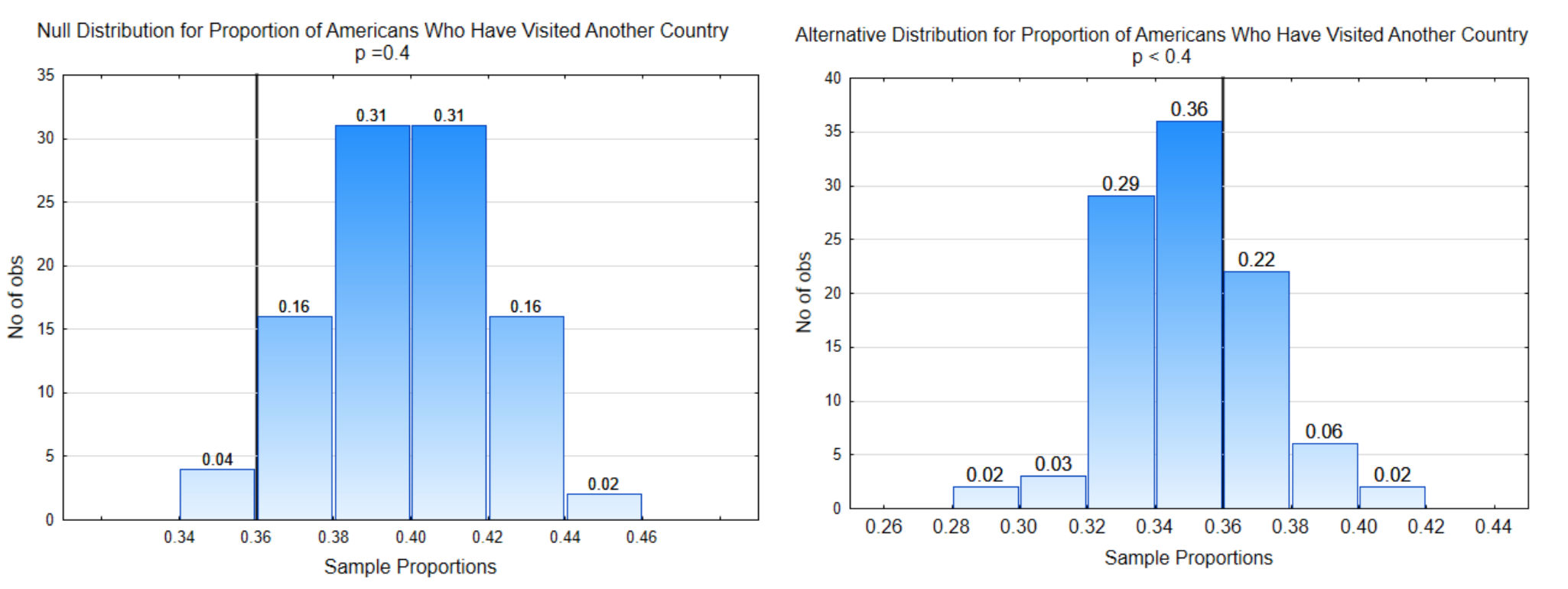
3. Etiquetado\(\alpha\),\(\beta\), y potencia. \(\alpha\)siempre se coloca en la distribución nula en el lado de la línea de decisión que está en la dirección de extremo. \(\beta\)siempre se coloca en la distribución alternativa en el lado de la línea de decisión que es opuesto a la dirección de extremo. El poder siempre se coloca en la distribución alternativa en el lado de la línea de decisión que está en la dirección de extremo.
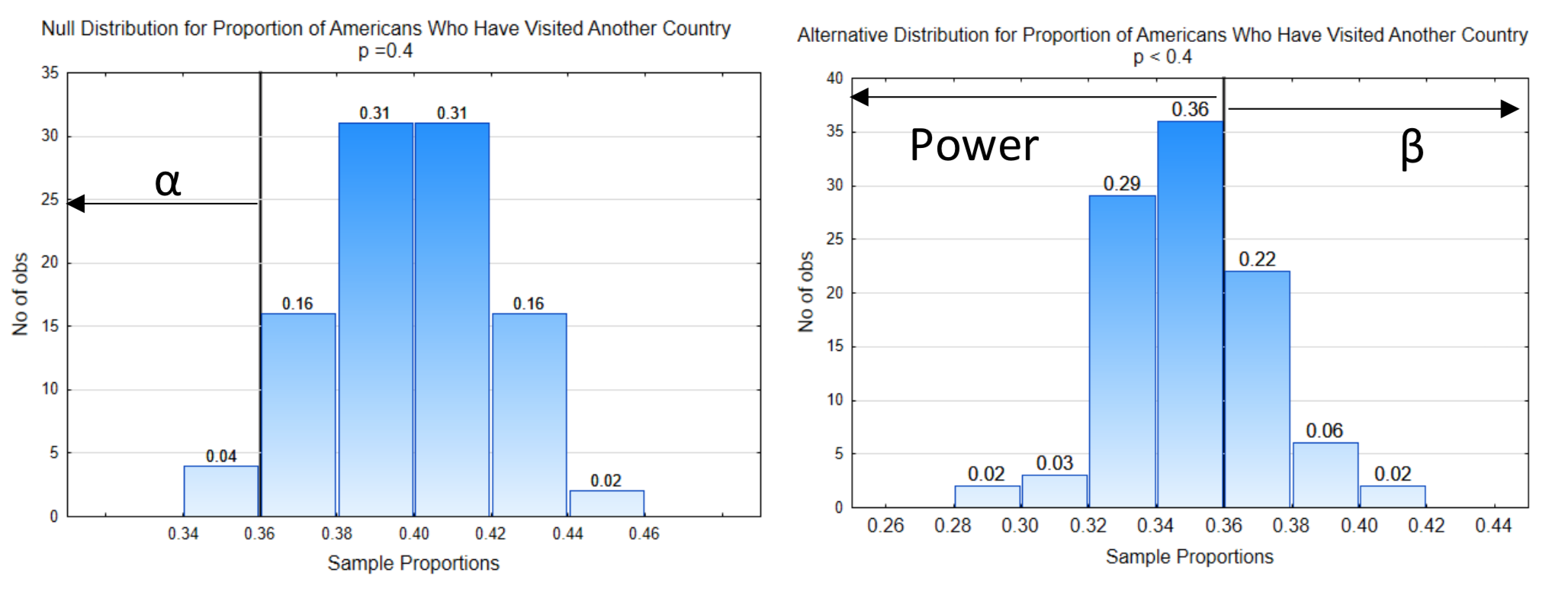
4. Identificar las probabilidades de\(\alpha\),\(\beta\), y el poder. Esto se hace añadiendo las proporciones en la parte superior de las barras.
En este ejemplo, la probabilidad para\(\alpha\) es 0.04. La probabilidad para\(\beta\) es de 0.30 (0.02 + 0.06 + 0.22). La probabilidad de poder es de 0.70 (0.02 + 0.03 + 0.29 + 0.36).
5. Encuentra el valor p. Se necesitan datos para probar la hipótesis, así que aquí están los datos: En una muestra de 200 personas, 72 han visitado otro país. La proporción muestral es\(\hat{p} = \dfrac{72}{200} = 0.36\). El valor p, que es la probabilidad de obtener los datos, o valores más extremos, asumiendo que la hipótesis nula es verdadera, siempre se coloca en la distribución nula y siempre apunta en la dirección del extremo.
En este ejemplo, el valor p se ha indicado en la distribución nula.
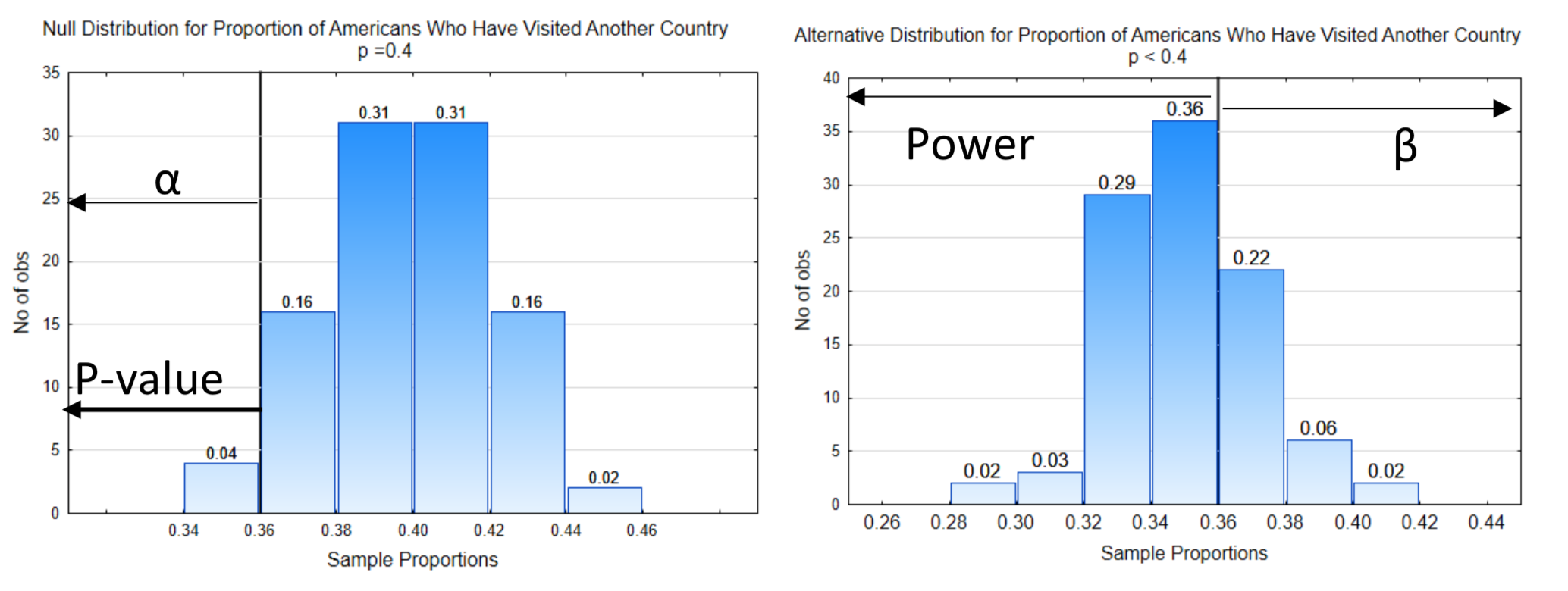
6. Tomar una decisión. La probabilidad para el valor p es 0.04. Para determinar qué hipótesis se sustenta en los datos, comparamos el valor p con alfa. Si el valor p es menor o igual a alfa, la evidencia apoya la hipótesis alternativa. En este caso, el valor p de 0.04 es igual a alfa que también es 0.04, por lo que esta evidencia apoya la hipótesis alternativa que lleva a concluir que la proporción de personas que han visitado otro país es menor al 40%.
7. Los errores y su consecuencia. Si bien este problema no es lo suficientemente grave como para tener consecuencias que importan, vamos a explorar, no obstante, las consecuencias de los diversos errores que se podrían cometer.
Debido a que la evidencia sustentaba la hipótesis alternativa, tenemos la posibilidad de cometer un error tipo I. Si hiciéramos un error tipo I significaría que pensamos que menos del 40% de los estadounidenses han visitado otro país, cuando en realidad el 40% lo ha hecho.
En contraste con esto, si nuestros datos hubieran sido 0.38 para que nuestro valor p fuera 0.20, entonces nuestros resultados habrían apoyado la hipótesis nula y podríamos estar cometiendo un error Tipo II. Este error significa que pensaríamos que el 40% de los estadounidenses había visitado otro país cuando, de hecho, la verdadera proporción sería menor que eso.
8. Reportando resultados. Los resultados estadísticos se reportan en una oración que indica si los datos son significativos, la hipótesis alternativa y la evidencia de apoyo, entre paréntesis, que en este punto incluyen el valor p y el tamaño de la muestra (n).
Para el ejemplo en el que\(\hat{p}\) = 0.36 escribiríamos, la proporción de estadounidenses que han visitado otros países es significativamente menor a 0.40 (p = 0.04, n = 200).
Para el ejemplo en el que\(\hat{p}\) = 0.38 escribiríamos, la proporción de estadounidenses que han visitado otros países no es significativamente menor a 0.40 (p= 0.20, n = 200).
En este punto, se necesita una breve explicación sobre la letra p. En el estudio de la estadística hay varias palabras que comienzan con la letra p y usan p como variable. La lista de palabras incluye parámetros, población, proporción, proporción muestral, probabilidad y valor p. Las palabras parámetro y población nunca se representan con una p. La probabilidad se representa con notación que es similar a la notación de función que aprendiste en álgebra, f (x), que se lee f de x. Para probabilidad, escribimos P (A) que se lee la probabilidad de evento A. Para distinguir entre el uso de p para proporción y p para valor p, prestar atención a la ubicación de la p. cuando se usa p en hipótesis, como\(H_0: p = 0.6\),\(H_1: p > 0.6\), significa la proporción de la población. Cuando se usa p en la conclusión, tal como la proporción es significativamente mayor a 0.6 (p = 0.01, n = 200), entonces la p en p = 0.01 se interpreta como un valor p. Si se da la proporción muestral, se representa como\(\hat{p}\) = 0.64.
Concluiremos este capítulo con una reflexión final sobre por qué somos formales en la prueba de hipótesis. Según Colquhoun (1971), “La mayoría de las personas necesitan toda la ayuda que puedan obtener para evitar que se hagan el ridículo al afirmar que su teoría favorita está corroborada por observaciones que no hacen nada por el estilo. Y la función principal de esa sección de estadística que trata de pruebas de significación es evitar que la gente se haga el tonto de sí misma”. (Verde, 1979).
Capítulo 1 Tareas
- Identificar cada uno de los siguientes como parámetro o estadística.
A. p es un
B.\(\bar{x}\) es un
C.\(\hat{p}\) es un
D.\(\mu\) es un - ¿Se escriben hipótesis sobre parámetros o estadísticas? _________________
- Una distribución de muestreo es un histograma de cuál de las siguientes?
______datos originales
______posibles estadísticas que podrían obtenerse al tomar muestras de una población - Escriba las hipótesis utilizando la notación apropiada para cada una de las siguientes hipótesis. Usar subíndices significativos al comparar dos parámetros poblacionales. Por ejemplo, al comparar hombres con mujeres, podrías usar guiones de m y w, por ejemplo\(p_m = p_w\).
4a. La media es mayor a 20. \(H_0\):\(H_1\):
4b. La proporción es menor a 0.75. \(H_0\):\(H_1\):
4c. La media para los estadounidenses es diferente a la media para los canadienses. \(H_0\):\(H_1\):
4d. La proporción para los mexicanos es mayor que la proporción para los estadounidenses. \(H_0\):\(H_1\):
4e. La proporción es diferente a 0.45. 4f. La media es inferior a 3000. \(H_0\):\(H_1\): - Si el valor p es menor que\(\alpha\),
5a. ¿qué hipótesis se soporta?
5b. son los datos significativos?
5c. qué tipo de error se podría hacer? - Por cada fila de la tabla se le da un valor p y un nivel de significancia (α). Determinar qué hipótesis se soporta, si los datos son significativos y qué tipo de error podría hacerse. Si un valor p dado no es un valor p válido (porque es mayor que 1), ponga una x en cada cuadro de la fila.
valor p \(\alpha\) Hipótesis\(H_0\) o\(H_1\) Significativo o No Significativo Error
Tipo I o Tipo II0.043 0.05 0.32 0.05 0.043 0.01 0.0035 0.01 0.043 0.10 0.15 0.10 5.6\(\times 10^{-6}\) 0.05 7.3256 0.01 - Por cada conjunto de información que se proporcione, escriba la frase final en la forma utilizada por los investigadores.
7a. \(H_1: p > 0.5, n = 350\), p - valor = 0.022,\(\alpha = 0.05\)
7b. \(H_1: p < 0.25, n = 1400\), p - valor = 0.048,\(\alpha = 0.01\)
7c. \(H_1: \mu > 20, n = 32\), p - valor =\(5.6 \times 10^{-5}\),\(\alpha = 0.05\)
7d. \(H_1: \mu \ne 20, n = 32\), p - valor =\(5.6 \times 10^{-5}\),\(\alpha = 0.05\) - Pruebe las hipótesis:
\(H_0: p = 0.5\)
\(H_1: p < 0.5\)
Utilizar un nivel de significancia del 2%.
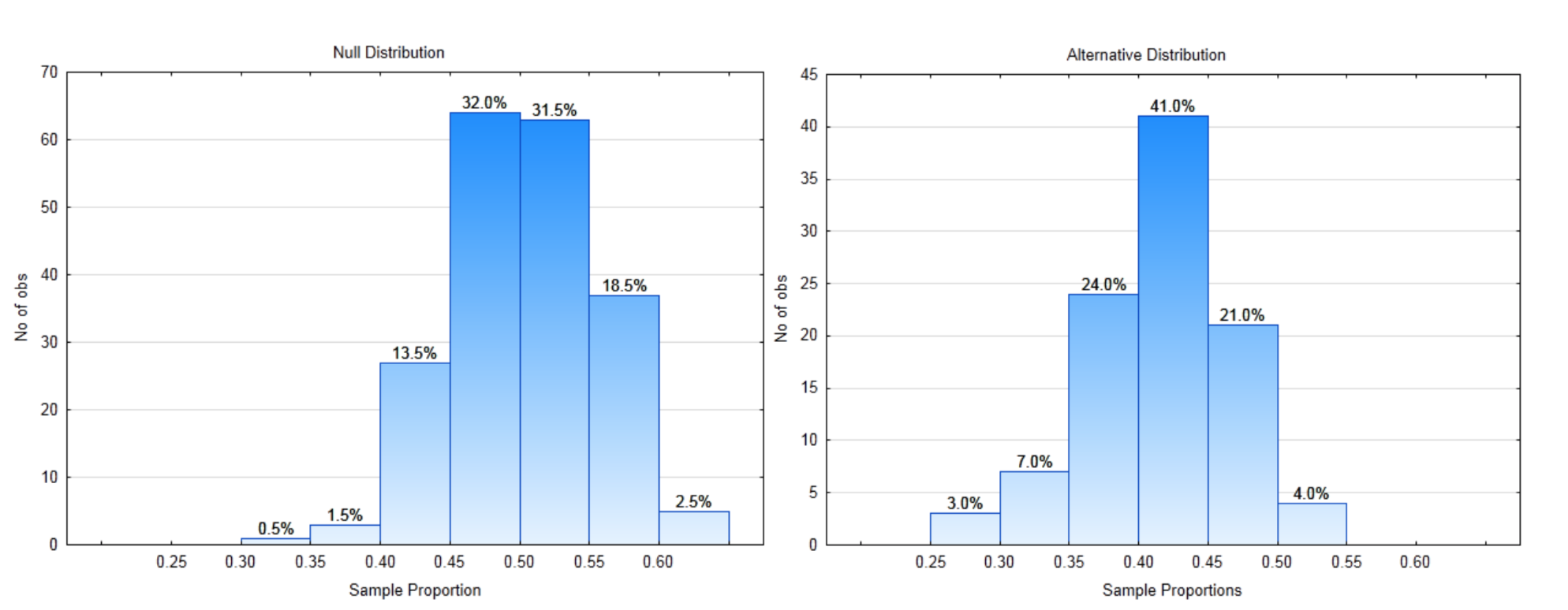
8a. ¿Cuál es la dirección del extremo?
8b. Etiquete cada distribución con una línea de regla de decisión. Identificar\(\alpha\) y encender la distribución adecuada.\(\beta\)
8c. ¿Cuál es el valor crítico?
8d. ¿Cuál es el valor de\(\alpha\)?
8e. ¿Cuál es el valor de\(\beta\)?
8f. ¿Cuál es el valor del Poder?
Los Datos: El tamaño de la muestra es 80. La proporción muestral es 0.45.
8g. Mostrar el valor p en la distribución apropiada.
8h. ¿Cuál es el valor del valor p?
8i. ¿Qué hipótesis se sustenta en los datos?
8j. ¿Los datos son significativos?
8k. ¿Qué tipo de error se pudo haber cometido?
8l. Escribe la frase de conclusión. - Pruebe las hipótesis:
\(H_0: \mu = 300\)
\(H_0: \mu > 300\)
Utilizar un nivel de significancia de 3.5%.
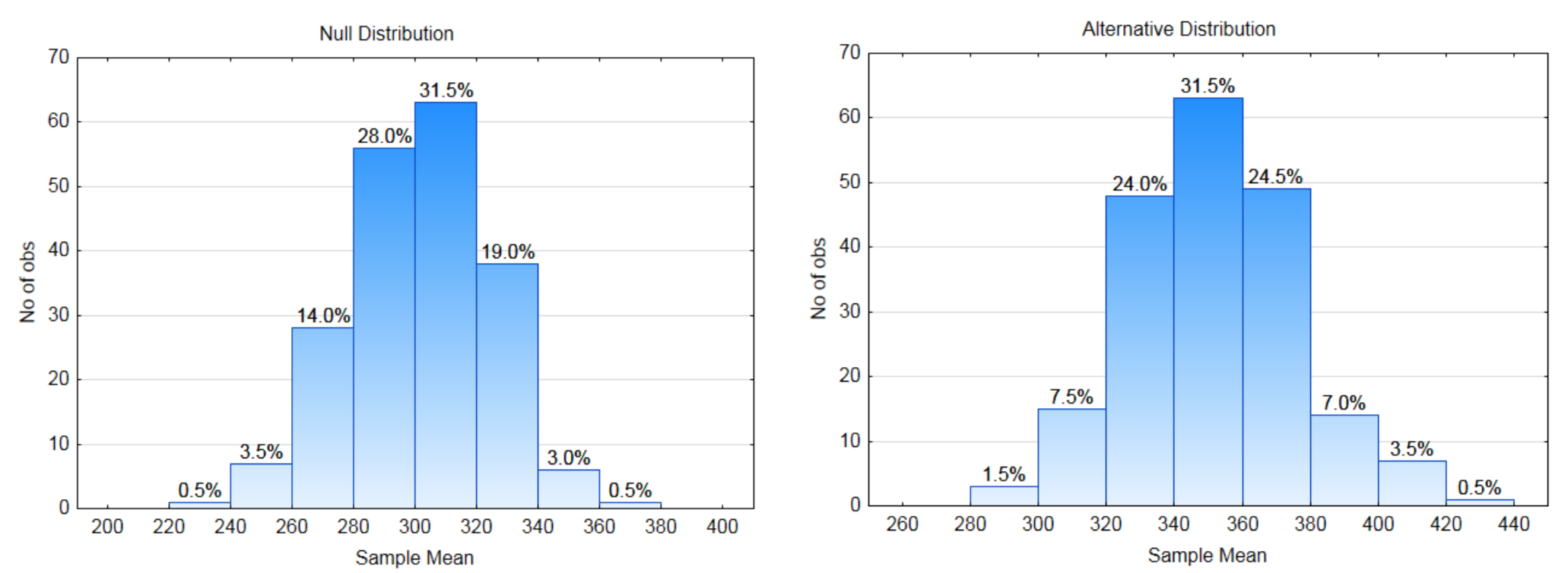
8a. ¿Cuál es la dirección del extremo?
8b. Etiquete cada distribución con una línea de regla de decisión. Identificar\(\alpha\) y encender la distribución adecuada.\(\beta\)
8c. ¿Cuál es el valor crítico?
8d. ¿Cuál es el valor de\(\alpha\)?
8e. ¿Cuál es el valor de\(\beta\)?
8f. ¿Cuál es el valor del Poder?
Los Datos: El tamaño de la muestra es 10. La media muestral es 360.
8g. Mostrar el valor p en la distribución apropiada.
8h. ¿Cuál es el valor del valor p?
8i. ¿Qué hipótesis se sustenta en los datos?
8j. ¿Los datos son significativos?
8k. ¿Qué tipo de error se pudo haber cometido?
8l. Escribe la frase de conclusión. - Pregunta: ¿Está mejorando la tasa de supervivencia al cáncer a cinco años para todas las razas?
.
Tasa de Supervivencia al Cáncer a 5 años. Según la American Cancer Society, en 1974-1976 la tasa de supervivencia a cinco años para todas las razas fue del 50%. Esto significa que el 50% de las personas a las que se les diagnosticó cáncer seguían vivas 5 años después. Estas personas aún podrían estar en tratamiento, podrían estar en remisión o podrían estar libres de enfermedades. (www.cancer.org/acs/groups/con... securedpdf.pdf Visto 5-29-13)
Diseño del estudio: Para determinar si las tasas de supervivencia están mejorando, se recopilarán datos de personas que hayan sido diagnosticadas con cáncer al menos 5 años antes del inicio de este estudio. El dato que se recogerá es si la gente sigue viva 5 años después de su diagnóstico. Los datos serán categóricos, es decir, la gente se pondrá en una de dos categorías, sobrevivirá o no sobrevivió. Supongamos que se examinan las historias clínicas de 100 personas diagnosticadas con cáncer. Utilizar un nivel de significancia de 0.02.
10a. Escriba las hipótesis que se utilizarían para demostrar que la proporción de personas que sobreviven al cáncer durante al menos cinco años después del diagnóstico es mayor a 0.5. Utilice el parámetro apropiado.
\(H_0:\)
\(H_1:\)
10b. ¿Cuál es la dirección del extremo?
10c. Etiquete las distribuciones de muestreo nulas y alternas a continuación con la línea de regla de decisión\(\alpha\),\(\beta\),, power.
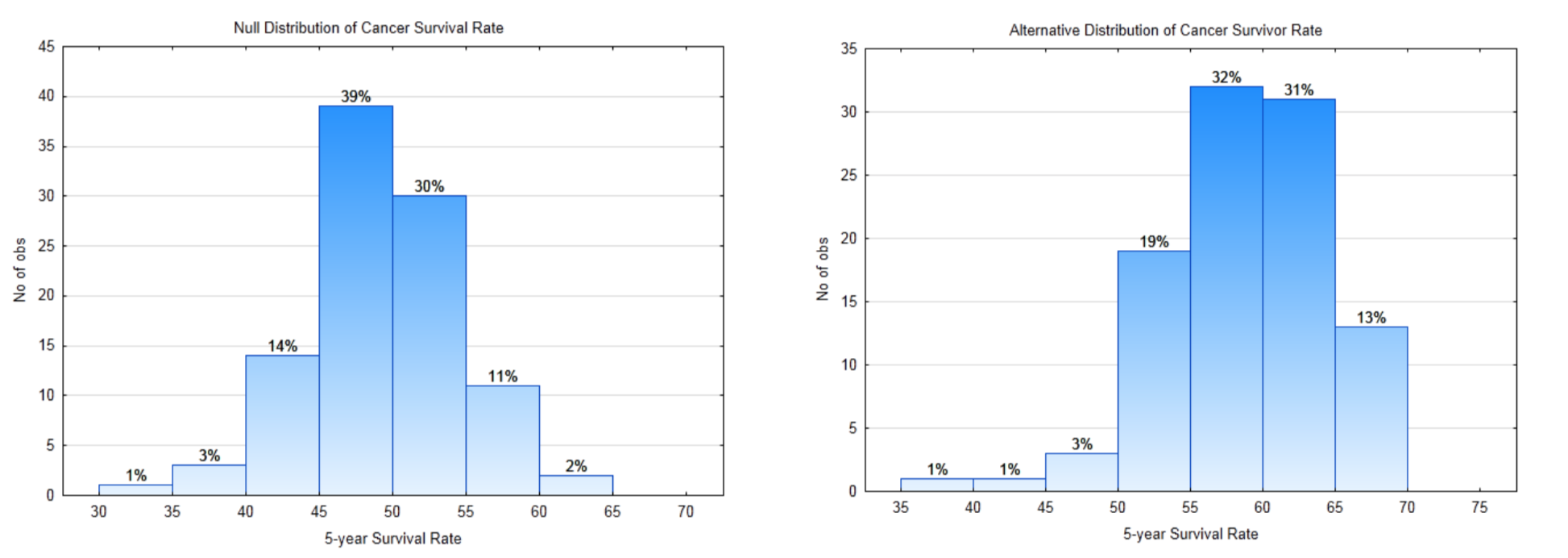
10d. ¿Cuál es el valor crítico?
10e. ¿Cuál es el valor de\(\alpha\)?
10f. ¿Cuál es el valor de\(\beta\)?
10g. ¿Cuál es el valor del Poder?Los datos: La tasa de supervivencia a 5 años es de 65%.
10h. ¿Cuál es el valor p para los datos?
10i. Escribe tu conclusión en el formato apropiado.
10j. ¿Qué tipo de error es posible?
10k. En inglés, explique la conclusión que se puede sacar sobre la pregunta. - Por qué el razonamiento estadístico es importante para un estudiante de negocios y un profesional
Desarrollado en Colaboración con Tom Phelps, Profesor de Economía, Matemáticas y Estadística Este tema se discute en ECON 201, Micro Economía.
Reunión Informativa 1.2
En términos generales, a medida que aumenta el precio de un artículo, hay menos unidades del artículo comprado. En términos económicos, hay menos “cantidad demandada”. La relación entre el cambio porcentual en la cantidad demandada y el cambio porcentual en el precio se denomina elasticidad de precio de la demanda. La fórmula es\(e_d = \dfrac{\%\Delta Q_d}{\%\Delta P}\). Por ejemplo, si un incremento del precio del 1% resultó en una disminución de 1.5% en la cantidad demandada, la elasticidad del precio es\(e_d = \dfrac{-1.5\%}{1\%}\) = −1.5. Es común que los economistas utilicen el valor absoluto de\(e_d\) ya que casi todos los\(e_d\) valores son negativos. La elasticidad es un número sin unidades llamado coeficiente de elasticidad.
La comida es un artículo que es esencial, por lo que la demanda siempre existirá, sin embargo comer fuera, que es más caro que comer en, no es tan esencial. El precio promedio de elasticidad de la demanda de alimentos para el hogar es de 0.51. Esto significa que un incremento de precio de 1% da como resultado una disminución de 0.51% en la cantidad demandada. Debido a que comer en casa es menos costoso que comer en restaurantes, no sería irrazonable suponer que a medida que aumentan los precios, la gente comería fuera con menos frecuencia. Si este es el caso, esperaríamos que la elasticidad de precio de la demanda por salir a comer fuera sea mayor que la de comer en casa. Pruebe la hipótesis de que la elasticidad media para los alimentos fuera de casa es mayor que para los alimentos en casa, lo que significa que el cambio de precios tiene un mayor impacto en comer fuera de casa. (www.ncbi.nlm.nih.gov/pmc/articles/PMC2804646/) (www.ncbi.nlm.nih.gov/pmc/arti... 46/table/tbl1/)
11a. Escriba las hipótesis que se utilizarían para demostrar que la elasticidad media para los alimentos fuera de casa es mayor a 0.51. Utilizar un nivel de significancia del 7%.
\(H_0:\)
\(H_1:\)
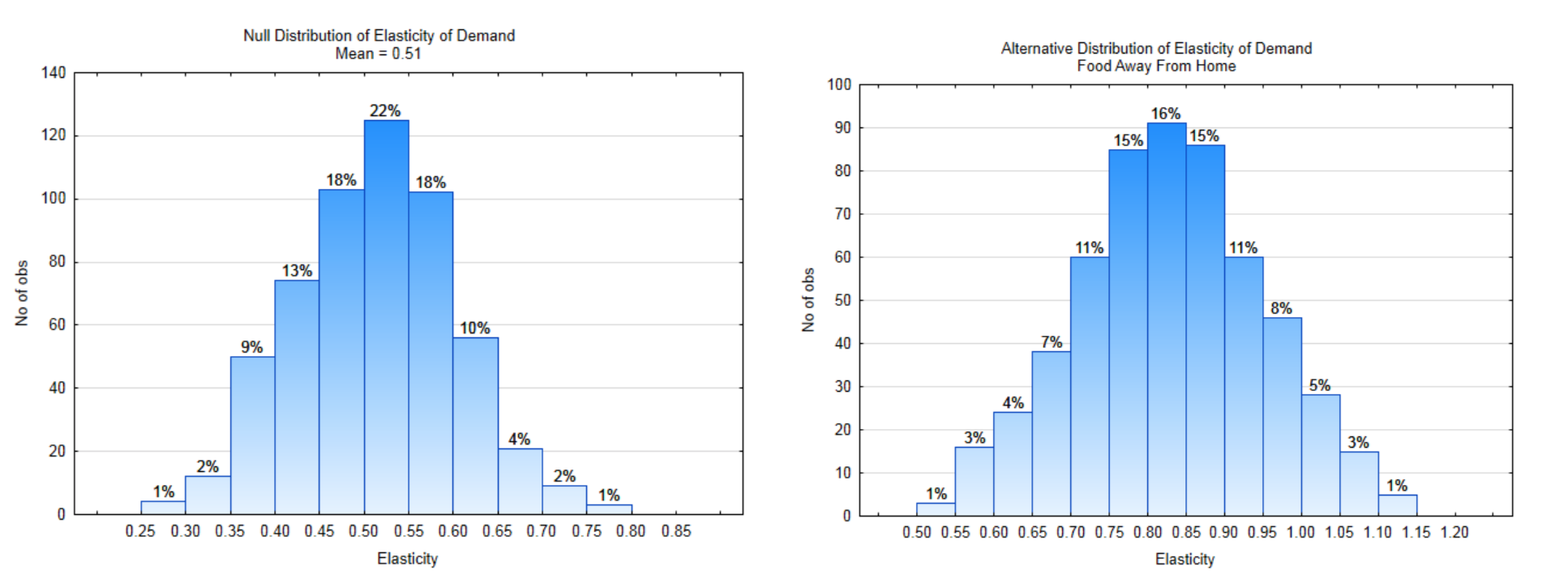
11b. Etiquete cada distribución con la línea de regla de decisión. Identificar\(\alpha\) y encender la distribución adecuada.\(\beta\)
11c. ¿Cuál es la dirección del extremo?
11d. ¿Cuál es el valor de\(\alpha\)?
11e. ¿Cuál es el valor de\(\beta\)?
11f. ¿Cuál es el valor del Poder?Los Datos: Una muestra de 13 restaurantes tuvo una elasticidad media de 0.80.
11g. Mostrar el valor p en la distribución apropiada.
11h. ¿Cuál es el valor del valor p?
11i. ¿Qué hipótesis se sustenta en los datos?
11j. ¿Los datos son significativos?
11k. ¿Qué tipo de error se pudo haber cometido?
11l. Escribe la frase de conclusión.


