9: Actividades en clase
- Page ID
- 150393
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capítulo 1 Datos y Estadísticas
- Una pregunta de encuesta preguntaba si estabas esperando el momento en que la mayoría de los autos en la carretera eran autos autónomos (autónomos), y la elección de las respuestas era sí o no.
a. ¿Los datos de las respuestas a esta pregunta son categóricos o cuantitativos?
b. ¿Es la estadística apropiada\(\hat{p}\) o\(\bar{x}\)?
c. En el cuadro que figura a continuación se dan las respuestas a 20 preguntas. Calcular el valor de la estadística apropiada utilizada para la respuesta sí.no si si si no no si no no si si no si no si no si si si no - En la cafetería de la escuela, un empleado contó el número de personas sentadas en cada mesa.
a. ¿Los datos de las respuestas a esta pregunta son categóricos o cuantitativos?
b. ¿Es la estadística apropiada\(\hat{p}\) o\(\bar{x}\)?
c. La siguiente tabla da el número en 10 tablas diferentes. Calcular el valor de la estadística apropiada.
5 6 8 7 4 1 7 8 3 1
Capítulo 1 Escritura de hipótesis
Nombre___________________________ Esfuerzo _____/4 Asistencia ____/1 Total ____/5
- El signo igual debe ir siempre en la hipótesis nula (\(H_0\))
- El signo igual puede no aparecer nunca en la hipótesis alternativa (\(H_1\))
- La hipótesis alternativa utiliza una de las siguientes: <, >,\(\ne\)
- Ambas hipótesis deben ser aproximadamente el mismo parámetro (media (μ) o proporción (p)). Si la hipótesis es sobre una proporción entonces usa un\(H_0: p = a\) número entre 0 y 1. Si la hipótesis es sobre una media, use el\(H_0: \mu = a\) número.
- El número en la hipótesis nula y alternativa debe ser el mismo.
Ejemplo: ¿Qué proporción de alumnos desayunaron hoy?
\(H_0: p = 0.60\)
\(H_1: p < 0.60\)
Ejemplo: ¿Cuál es el promedio de calorías que consumen hoy en día los estudiantes para el desayuno?
\(H_0: \mu = 200\)
\(H_1: \mu > 200\)
Escribe tus hipótesis para cada pregunta. Utilizar cada una de las tres desigualdades al menos una vez.
- ¿Cuál es la frecuencia cardíaca promedio de los estudiantes universitarios?
\(H_0: \)
\(H_1: \)
- Dada la elección entre la humanidad crear un futuro fantástico con tecnología o sufrir un colapso de la sociedad debido al agotamiento de los recursos y otros problemas ambientales, ¿qué proporción de estudiantes universitarios hipotetiza cree que el futuro será fantástico?
\(H_0: \)
\(H_1: \)
- ¿Cuál es el tiempo promedio, en minutos, que tardan los alumnos en llegar a la escuela por la mañana?
\(H_0: \)
\(H_1: \)
- ¿Qué proporción de estudiantes comen masa cruda para galletas?
\(H_0: \)
\(H_1: \)
Capítulo 1 Distribuciones de muestreo
1. En la distribución a la derecha: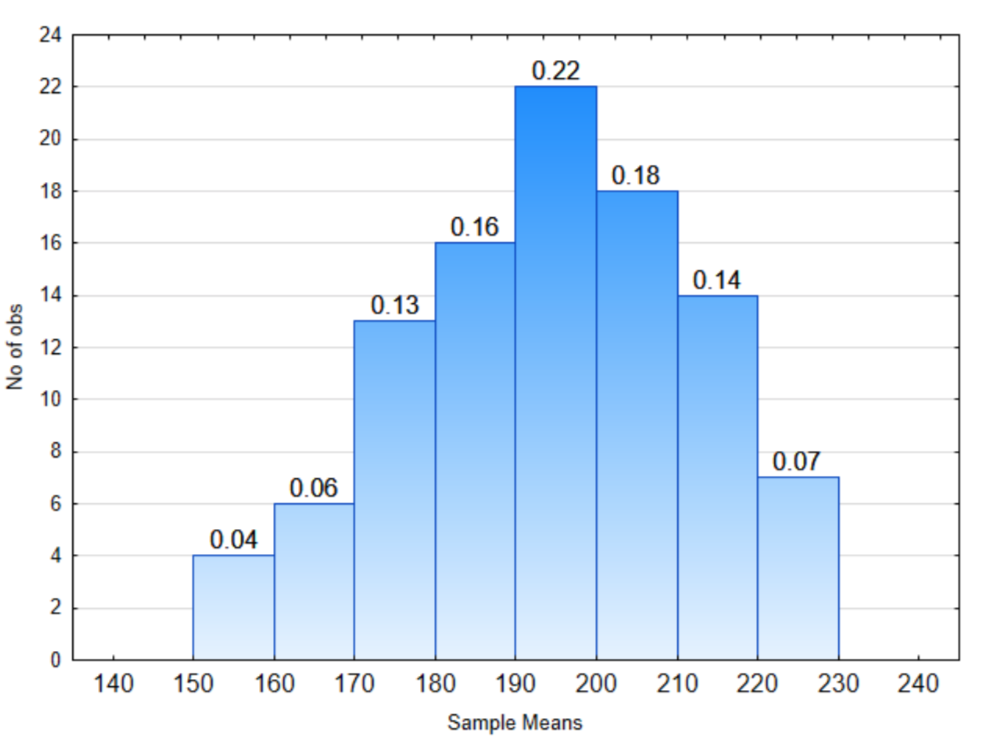
¿Qué proporción de medias muestrales estará entre 150 y 170?
¿Qué proporción de medias muestrales estará entre 200 y 230?
¿Qué proporción de medias muestrales estará entre 150 y 230?
2. En la distribución a la derecha: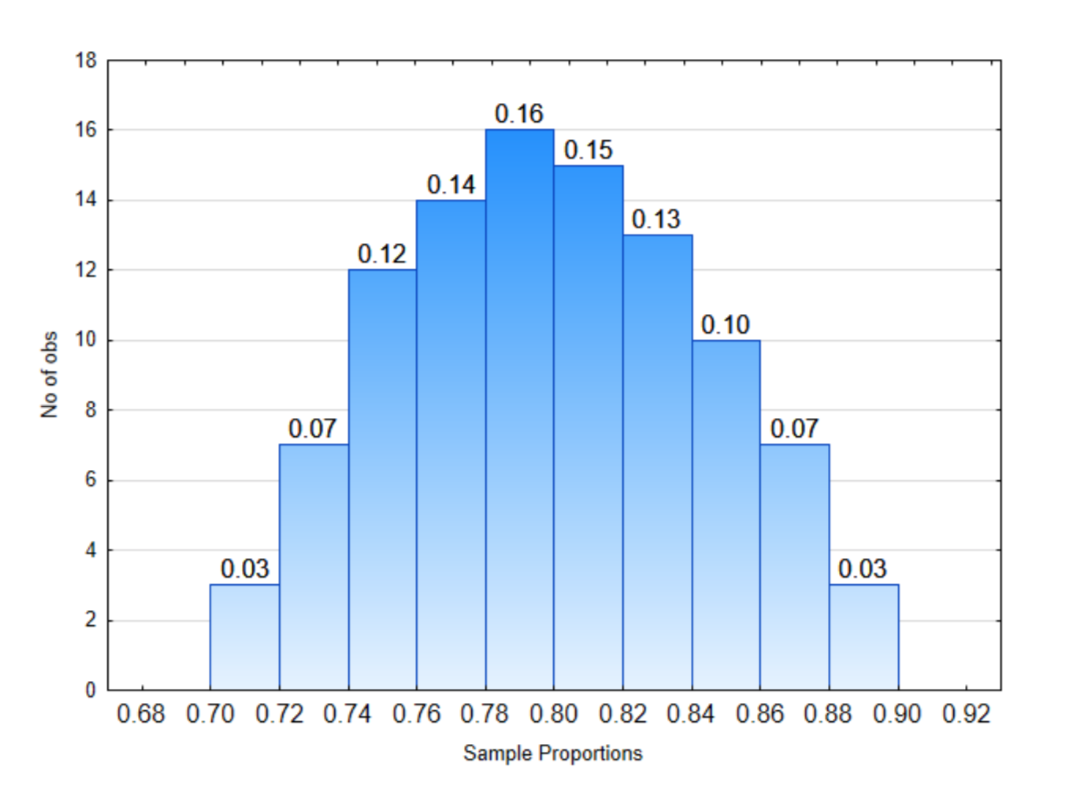
¿Qué proporción de proporciones muestrales estará entre 0.70 y 0.74?
¿Qué proporción de proporciones muestrales estará entre 0.84 y 0.90?
¿Qué proporción de proporciones de muestra será menor a 0.70?
Capítulo 2 valores p y niveles de significancia
- Por cada fila de la tabla se le da un valor p y un nivel de significancia (\(\alpha\)). Determinar qué hipótesis se soporta, si los datos son significativos y qué tipo de error podría hacerse. Si un valor p dado no es un valor p válido, ponga una x en cada cuadro de la fila.
p - valor \(\alpha\) Hipótesis\(H_0\) o\(H_1\) Significativo o No Significativo Error
Tipo I o Tipo II0.48 0.05 0.023 0.10 6.7E-6 0.01 Identificar cada uno como verdadero o falso si los datos no son significativos
_____ La hipótesis nula es definitivamente cierta
_____ La hipótesis alternativa es definitivamente cierta
_____ La hipótesis alternativa es rechazada
_____ La hipótesis nula no fue rechazada
_____El valor p es mayor que\(\alpha\)
- Por cada fila de la tabla se le da un valor p y un nivel de significancia (\(\alpha\)). Determinar qué hipótesis se soporta, si los datos son significativos y qué tipo de error podría hacerse. Si un valor p dado no es un valor p válido, ponga una x en cada cuadro de la fila.
p - valor \(\alpha\) Hipótesis\(H_0\) o\(H_1\) Significativo o No Significativo Error
Tipo I o Tipo II0.048 0.05 0.0023 0.10 6.70 0.01
Identificar cada uno como verdadero o falso si los datos no son significativos
_____ La hipótesis nula es definitivamente cierta
_____ La hipótesis alternativa es definitivamente cierta
_____ La hipótesis alternativa es rechazada
_____ La hipótesis nula no fue rechazada
_____El valor p es mayor que\(\alpha\)
Prueba de hipótesis elemental, Ejemplo 1 Arsénico
Briefing: El arsénico es un elemento natural y también un elemento producido por humanos (por ejemplo, fracking, combustión de carbón) que se puede encontrar en las aguas subterráneas. Causa una variedad de problemas de salud y puede llevar a la muerte. El límite de EPA es de 10 ppb, lo que significa que 10 ppb o más no es seguro. Problema: El fracking se inició en tu comunidad. Un año después, la enfermedad en la comunidad lleva a los funcionarios del departamento de salud a analizar su agua para determinar si está contaminada con arsénico. El funcionario tomará 5 muestras de agua durante los próximos 2 meses y decidirá si se tiene agua segura o insegura en base al promedio de estas muestras. Las hipótesis a probar son:\(H_0: \mu = 10\) (No seguro)\(H_1: \mu < 10\) (Seguro). El nivel de significación es:\(\alpha = 0.12\).
Supongamos que estas son las dos distribuciones posibles que existen.
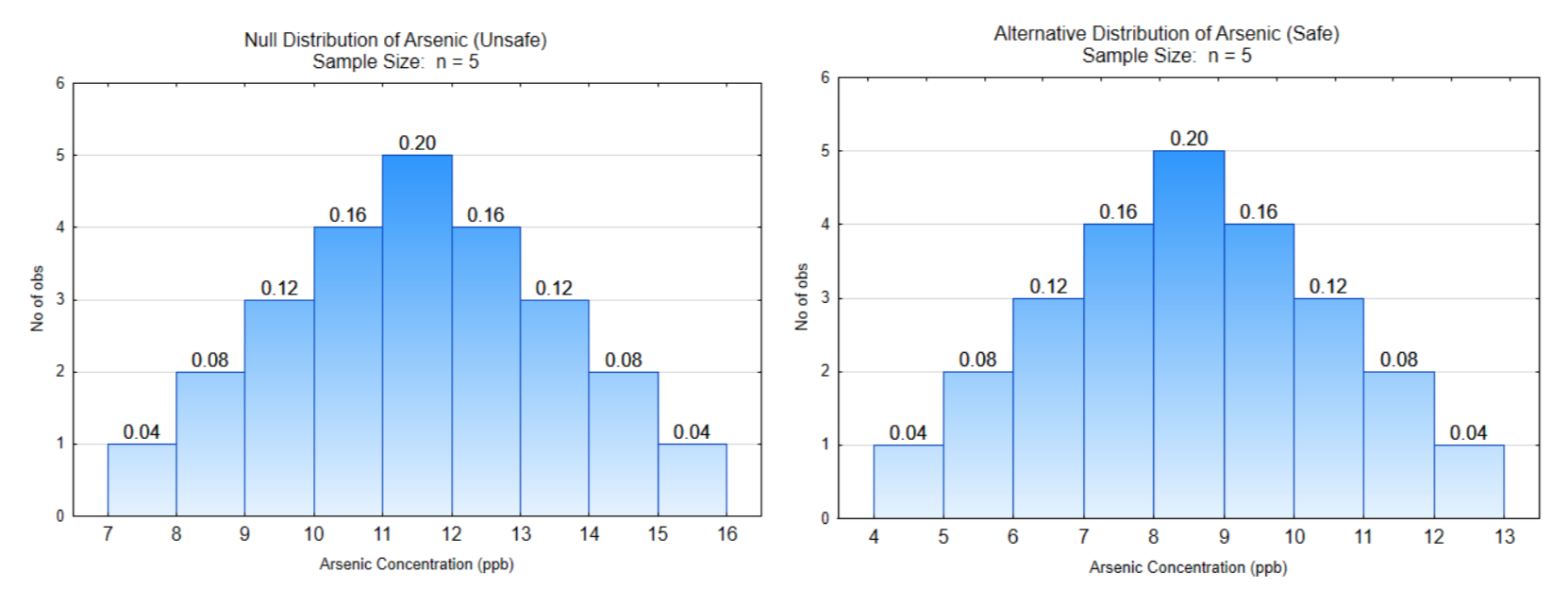
¿Cuál es la dirección del extremo?
Mostrar la línea de decisión en ambas distribuciones.
¿Cuál es el valor crítico?
Etiqueta\(\alpha\),\(\beta\), y poder
¿Cuál es la probabilidad de\(\alpha\)?
¿Cuál es la probabilidad de\(\beta\)?
¿Cuál es el poder?
¿Cuál es la consecuencia de un error de Tipo I?
¿Cuál es la consecuencia de un error Tipo II?
Datos: Lo que se selecciona del contenedor que se pasó alrededor del aula
Escribe una oración conclusiva:
¿Qué decisión tomas sobre tu casa y el suministro de agua?
Prueba de hipótesis elemental, Ejemplo 2: ¿La mayoría de la gente en EU cree que es hora de un nuevo sistema de votación?
Briefing: El sistema de votación por pluralidad se ha utilizado en este, y en otros países, desde que se formaron las democracias. No obstante, este sistema ha llevado a la dominación de dos partidos que no necesariamente reflejan las opiniones de los ciudadanos. Algunos países, como Nueva Zelanda, y algunos estados y comunidades de Estados Unidos han adoptado otros sistemas de votación que permiten una mejor representación. Imagínese una encuesta en la que se le preguntara a la gente si piensa que es momento de cambiar el sistema de votación como solución al partidismo decisivo que existe actualmente en EU. El objetivo es determinar si la mayoría de los electores están listos para explorar sistemas alternativos de votación. Las hipótesis son:\(H_0: p = 0.50\),\(H_1: p > 0.50\),\(\alpha = 0.07\).
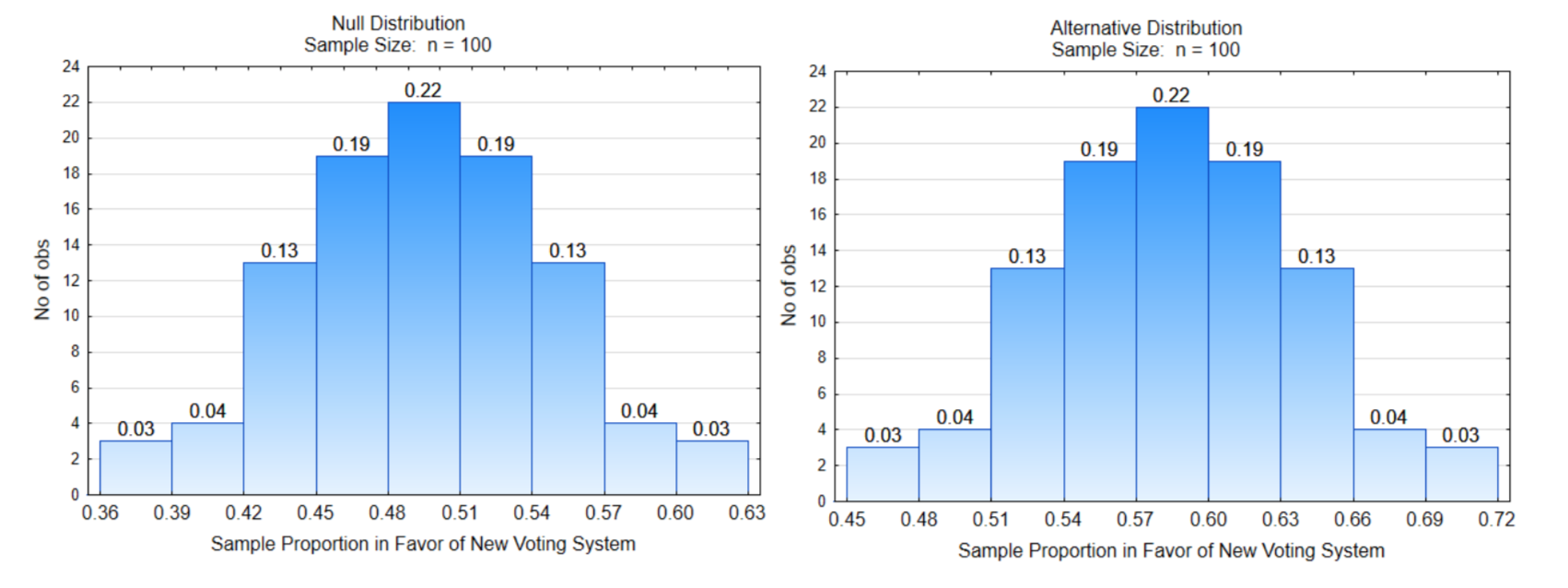
¿Cuál es la dirección del extremo?
Mostrar la línea de decisión en ambas distribuciones.
¿Cuál es el valor crítico?
Etiqueta\(\alpha\),\(\beta\), y poder
¿Cuál es la probabilidad de\(\alpha\)?
¿Cuál es la probabilidad de\(\beta\)?
¿Cuál es el poder?
¿Cuál es la consecuencia de un error de Tipo I?
¿Cuál es la consecuencia de un error Tipo II?
Datos: 54 de cada 100 votantes querían explorar sistemas alternativos de votación.
¿Cuál es la proporción muestral?
Escribe una oración conclusiva:
Capítulo 2 Mesas de diseño
- En un esfuerzo por determinar qué estrategia es más efectiva para perder peso, un investigador asigna aleatoriamente sujetos a uno de cuatro grupos. Un grupo (ejercicio) se involucrará en un programa de ejercicio regular, un segundo grupo será alimentado con una dieta balanceada (alimento) pero con porciones de tamaño apropiado, un tercer grupo (ejercicio y comida) utilizará tanto el programa de ejercicios como la dieta balanceada, mientras que el cuarto grupo (sin cambios) no cambiará su dieta o ejercicio.
Mesa de diseño de investigación Pregunta de investigación: Tipo de Investigación Estudio Observacional Experimento
Observacional Experimento
Manipulativo¿Cuál es la variable respuesta? ¿Cuál es el parámetro que se calculará? Proporción media Enumerar posibles variables de confusión. Variables de agrupamiento/explicativas 1 (si están presentes) Niveles: - La gente se emociona cuando un joven atleta logra un gran éxito pero siempre existe la cuestión de si los mejores atletas universitarios estaban en realidad entre los mejores atletas jóvenes. Si se hicieran entrevistas a atletas del equipo universitario titular de escuelas de la División 1 y se les preguntara si se les consideraba atletas superiores cuando tenían 10 años en su deporte, ¿la proporción que tuvieron éxito de niño pequeño sería diferente para hombres y mujeres?
Mesa de diseño de investigación Pregunta de investigación: Tipo de Investigación Estudio Observacional Experimento
Observacional Experimento
Manipulativo¿Cuál es la variable respuesta? ¿Cuál es el parámetro que se calculará? Proporción media Enumerar posibles variables de confusión. Variables de agrupamiento/explicativas 1 (si están presentes) Niveles:
Capítulo 2 Números aleatorios
1. Se realizará una encuesta en nuestro colegio. La administración espera diferentes respuestas de estudiantes de inicio corriendo, estudiantes tradicionales, estudiantes que regresan y veteranos. Se realizarán muestreos de cada uno de estos grupos.
¿Qué método de muestreo se está utilizando?
Si hay 1320 veteranos (1-1320), ¿cuáles son los números de los 3 primeros veteranos seleccionados al azar si se usa un valor semilla de 3?
2. Los datos de series de tiempo se seleccionarán con 5 años de diferencia para que los datos sean independientes. ¿Cuáles son los números de los primeros 3 años de datos seleccionados aleatoriamente si el primer año de datos es 1960? Utilice un valor semilla de 4.
Capítulo 2 Comparar y Contraste Métodos de Muestreo
Nombre___________________________ Esfuerzo_____/5 Asistencia ____/1 Total ___/6
Un debate actual en Washington es si construir terminales de exportación de carbón para que el carbón extraído en Montana y Wyoming pueda enviarse en tren a la costa de Washington, Oregón o Columbia Británica y luego exportarse a Asia. Algunas preocupaciones incluyen trenes largos que serán una interrupción constante del tráfico, el polvo de carbón de los trenes contaminará el aire cerca de las líneas ferroviarias, contaminación del agua que destruirá la industria pesquera y pesquera, y la preocupación de que el carbón contribuya al cambio climático. Supongamos que un grupo de trabajo de 100 personas de Idaho, Washington, Oregón y Columbia Británica se reúnen para determinar una política regional para esta situación. El grupo de trabajo está integrado por funcionarios gubernamentales (G) y ciudadanos públicos (C). A todos ellos se les ha asignado un número del 1 al 100. Todos los muestreos se realizarán con reemplazo. Eso significa que puede usar el mismo número dos veces dentro de un método de muestreo. Esta actividad está pensada para permitirle comparar y contrastar los 4 métodos de muestreo.
| Grupo 1 Idaho |
Grupo 2 Washington |
Grupo 3 Oregón |
Grupo 4 Columbia Británica |
||||
| 1 -C | Sin Carbón | 23 -G | Sin Carbón | 49 -G | Terminales | 71 -C | Terminales |
| 2 -C | Terminales | 24 -C | Terminales | 50 -G | Sin Carbón | 72 -G | Terminales |
| 3 -C | Terminales | 25 -G | Sin Carbón | 51 -G | Sin Carbón | 73 -C | Sin Carbón |
| 4 -C | Terminales | 26 -G | Sin Carbón | 52 -G | Sin Carbón | 74 -G | Terminales |
| 5 -C | Sin Carbón | 27 -C | Terminales | 53 -C | Sin Carbón | 75 -C | Terminales |
| 6 -C | Terminales | 28 -G | Sin Carbón | 54 -C | Terminales | 76 -C | Terminales |
| 7 -C | Terminales | 29 -G | Sin Carbón | 55 -G | Sin Carbón | 77 -C | Terminales |
| 8 -G | Sin Carbón | 30 -G | Sin Carbón | 56 -C | Sin Carbón | 78 -G | Terminales |
| 9 -G | Terminales | 31 -C | Sin Carbón | 57 -G | Sin Carbón | 79 -G | Terminales |
| 10 -G | Sin Carbón | 32 -C | Terminales | 58 -G | Sin Carbón | 80 -C | Terminales |
| 11 -C | Terminales | 33 -G | Terminales | 59 -G | Sin Carbón | 81 -C | Sin Carbón |
| 12 -G | Sin Carbón | 34 -G | Terminales | 60 -C | Sin Carbón | 82 -G | Terminales |
| 13 -G | Terminales | 35 -G | Terminales | 61 -C | Terminales | 83 -G | Terminales |
| 14 -G | Sin Carbón | 36 -G | Terminales | 62 -G | Sin Carbón | 84 -C | Sin Carbón |
| 15 -G | Terminales | 37 -C | Terminales | 63 -C | Sin Carbón | 85 -C | Sin Carbón |
| 16 -G | Sin Carbón | 38 -G | Terminales | 64 -C | Terminales | 86 -G | Terminales |
| 17 -C | Terminales | 39 -C | Terminales | 65 -C | Terminales | 87 -C | Sin Carbón |
| 18 -G | Sin Carbón | 40 -G | Sin Carbón | 66 -G | Sin Carbón | 88 -C | Terminales |
| 19 -G | Terminales | 41 -G | Sin Carbón | 67 -G | Terminales | 89 -G | Sin Carbón |
| 20 -G | Terminales | 42 -G | Terminales | 68 -G | Sin Carbón | 90 -G | Sin Carbón |
| 19 -C | Terminales | 43 -G | Sin Carbón | 69 -C | Terminales | 91 -G | Sin Carbón |
| 22 -G | Sin Carbón | 44 -C | Sin Carbón | 70 -C | Terminales | 92 -C | Terminales |
| 45 -C | Sin Carbón | 93 -G | Sin Carbón | ||||
| 46 -C | Sin Carbón | 94 -C | Sin Carbón | ||||
| 47 -G | Sin Carbón | 95 -G | Sin Carbón | ||||
| 48 -G | Sin Carbón | 96 -G | Terminales | ||||
| 97 -G | Terminales | ||||||
| 98 -C | Terminales | ||||||
| 99 -C | Terminales | ||||||
| 100 -G | Terminales | ||||||
1. Muestra aleatoria simple
Usa tu calculadora con una semilla de 23 para seleccionar aleatoriamente una muestra de tamaño 10. El número más bajo es 1 y el más alto es 100. Enumere los números seleccionados y luego determine la proporción de la muestra que está frente a las terminales de carbón (Sin Carbón).
Número: _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,
N o T _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,
Proporción que es contra las terminales de carbón:\(\hat{p} =\) _____
2. Muestra aleatoria estratificada
Usa tu calculadora con una semilla de 13. El mínimo es 1 y el máximo es 100. Poner los números aleatorios en los estratos apropiados. Cuando se llena un estrato, ignora otros números que pertenecen a él.
Ciudadanos: Número _____, _____, _____, _____, _____,
N o T _____, _____, _____, _____, _____,
Gobierno: Número _____, _____, _____, _____, _____,
N o T _____, _____, _____, _____, _____,
Proporción (uso de ciudadanos y funcionarios de gobierno combinados) que está en contra de terminales de carbón: \(\hat{p} =\)_____
3. Muestra aleatoria sistemática
Utilice un método de muestreo de 1 en K, con k = 10 para seleccionar aleatoriamente una muestra de tamaño 10. Para determinar el primer número seleccionado, usa tu calculadora con una semilla de 18, un mínimo de 1 y un máximo de 10. Determinar la proporción de la muestra que está frente a las terminales de carbón.
Número: _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,
N o T _____, _____, _____, _____, _____, _____, _____, _____, _____, _____,
Proporción que es contra terminales de carbón:\(\hat{p} =\) _____
4. Muestreo en raci
Usa tu calculadora con un valor semilla de 33 para seleccionar aleatoriamente uno de los grupos (1-4). ¿Qué grupo se selecciona? _____________. ¿Cuál es la proporción muestral del grupo seleccionado que está frente a las terminales de carbón? \(\hat{p} =\)_____
Capítulo 3 Histogramas y gráficas de caja
Nombre___________________________ Esfuerzo_____/5 Asistencia ____/1 Total ___/6
Los resultados de un examen sobre los Capítulos 2 y 3 de una clase de estadística se muestran en la siguiente tabla. Los números representan el porcentaje de puntos posibles que obtuvo el estudiante.
| 76.8 | 91.5 | 98.8 | 97.6 | 76.8 | 93.9 | 57.3 | 86.6 | 90.2 |
| 93.9 | 93.9 | 82.9 | 92.7 | 89.0 | 72.0 | 57.3 | 93.9 | 92.7 |
| 93.9 | 81.7 | 63.4 | 68.3 | 85.4 | 50.0 | 84.1 | 90.2 | 86.6 |
| 97.6 | 84.1 | 81.7 | 95.1 | 87.8 | 75.6 | 92.7 | 73.2 | 91.5 |
Valor bajo ___________ Valor alto _____________
Hacer una distribución de frecuencias. Utilice la notación de intervalos para los límites [inferior, superior).
| Clases | |
Hacer un histograma. Etiquetar completamente.
Use su calculadora para completar la siguiente tabla ingresando los datos originales en las listas.
|
Media |
|
|
Desviación estándar Sx |
|
|
Mínimo |
|
|
Q1 |
|
|
Mediana |
|
|
Q3 |
|
|
Máximo |
Hacer un diagrama de caja. Etiquetar completamente.
Capítulo 4 Teoría Inferencial
Pregunta 2: ¿Más del 70% de los estadounidenses beben té (ya sea caliente o helado)?
a. Escribe tu hipótesis nula y alternativa:
b. Buscar P (S): c. Buscar P (F):
d. Si tomaste una muestra de 7 personas, ¿cuál es la probabilidad de que el orden exacto sea SFSSFSS? Es decir, encontrar P (SFSSFSS).
e. ¿Cuántas combinaciones hay para 5 éxitos en una muestra de 7 personas?
f. ¿Cuál es la probabilidad de que consigas 5 éxitos en una muestra de 7 personas?
g. Hacer una distribución binomial por el número de éxitos en una muestra de 7 personas.
h. ¿Cuál es la media y la desviación estándar para esta distribución?
i. Terminar la frase final si hubo 5 éxitos en una muestra de 7 personas. En el nivel de significancia del 5%, la proporción de estadounidenses que toman té __________________________________________________________________________________________________________________________________________
Capítulo 4 Teoría Inferencial — Pruebas de Hipótesis
Los residentes del noroeste del Pacífico suelen estar preocupados por el tema de la sustentabilidad. Si una encuesta a 400 individuos del noroeste del Pacífico resultó en 296 quienes dijeron que toman decisiones basadas en ser sustentables, entonces pruebe la hipótesis de que más del 67% de los individuos en esta región toman decisiones basadas en ser sustentables.
Pruebe las hipótesis (\(H_0: p = 0.67\)\(H_1: p > 0.67\)) utilizando tres métodos diferentes y un nivel de significancia de 0.05. Para cada método, se le preguntará qué hipótesis se apoya.
1a. Distribución binomial: Utilice la distribución binomial para calcular el valor p exacto con base en los datos (296 de 400).
__________________________ ___________________ Valor p de entrada de
calculadora
¿Qué hipótesis se sustenta en los datos? Elige 1:\(H_0\)\(H_1\)
1b. Aproximación Normal: Utilice la aproximación normal a la distribución binomial para calcular el valor p aproximado con base en los datos (296 de 400). Proporcionar la información solicitada.
\(\mu = np = \),\(\sigma = \sqrt{npq} =\)
Sustitución de fórmula valor z valor p
¿Qué hipótesis se sustenta en los datos? Elige 1:\(H_0\)\(H_1\)
1c. Distribución de Muestreo para Proporciones de Muestra: Encuentra el valor p usando proporciones de muestra para los datos (296 de 400). Proporcionar la información solicitada.
Proporción de muestra
Sustitución de fórmula valor z valor p
¿Qué hipótesis se sustenta en los datos? Elige 1:\(H_0\)\(H_1\)
Un estudiante de la UC Santa Bárbara (http://www.culturechange.org/cms/content/view/704/62/) hizo algunas investigaciones sobre los vasos rojos de plástico que la gente usa para bebidas en fiestas. Estas tazas están hechas de Poliestireno, que no se pueden reciclar en Santa Bárbara. Muchas de las copas terminan en el relleno sanitario, pero algunas terminan en el océano. En la cercana localidad universitaria de Isla Vista, el investigador estimó que el promedio de tazas utilizadas por persona por año fue de 58. Supongamos que la desviación estándar es 8.
En un esfuerzo por cambiar la cultura, supongamos que se utilizó una campaña educativa para reducir el número de tazas rojas al incentivar la compra de bebidas en latas (ya que pueden reciclarse). Para determinar si esto es efectivo, una muestra aleatoria de 16 estudiantes realizará un seguimiento del número de tazas rojas que utilizan durante todo el año. Las hipótesis que se pondrán a prueba son:\(H_0: \mu = 58\)\(H_1: \mu < 58\)\(\alpha = 0.05\)
2a. ¿Cuál es la media de la distribución muestral de las medias muestrales? \(\mu_{\bar{x}}\)________
2b. ¿Cuál es la desviación estándar de la distribución muestral de las medias de la muestra? \(\sigma_{\bar{x}}\)_________
2c. Dibujar y etiquetar una distribución normal que muestre la media y las tres primeras desviaciones estándar (errores estándar) en cada lado de la media para la distribución de medias muestrales de 16 estudiantes.
2d, Probar la hipótesis si la media muestral de los 16 estudiantes es 55 utilizando un nivel de significancia de\(\alpha = 0.05\).
Sustitución de fórmula valor z valor p
2e. Con base en los resultados de este experimento, ¿ha habido una reducción en el uso de copas rojas? Elija 1: Sí No
Capítulos 5 y 6 Práctica mixta con pruebas de hipótesis e intervalos de confianza
Para cada problema, proporcione las hipótesis y pruebe las hipótesis calculando el estadístico de prueba y el valor p. Rellena todos los espacios en blanco en la siguiente oración. Además, dé la respuesta de la calculadora entre paréntesis para el estadístico de prueba y el valor p. Esto no será corregido ni calificado sino que te ayudará a prepararte para el examen.
1. Un estudiante leyó que en la zona de la bahía de California, la persona promedio produce 2 libras de basura al día. La estudiante creía que producía menos que eso pero quería probar estadísticamente su hipótesis. Recolectó datos en 10 días seleccionados al azar. Uso\(\alpha = 0.05\).
| 2.0 | 2.3 | 1.9 | 1.9 | 2.3 |
| 1.2 | 2.3 | 2.1 | 1.7 | 1.8 |
\(H_0:\)
\(H_1:\)
¿Qué significa la muestra? Media de la Muestra ______________
¿Cuál es la desviación estándar de la muestra? Desviación estándar de la muestra______________
Prueba de sustitución de fórmulas Valor estadístico valor p
Calculadora:
Test Statistic value valor p
La cantidad promedio de basura producida diariamente por el alumno ___________ significativamente menor a 2 libras (t = __________, p = _____________, n=_______________).
¿Cuál es el intervalo de confianza del 95% para la cantidad de basura que produce?
Margen de sustitución de fórmula del intervalo de confianza de
Intervalo de confianza de la calculadora: __________________
2. Un salario digno es la tarifa por hora que un individuo debe ganar para mantener a su familia, si es el único proveedor y está trabajando a tiempo completo. En 2005, se estimó que 33% de las ofertas de trabajo tenían salarios inadecuados (por debajo del salario digno). Un investigador desea determinar si ese sigue siendo el caso. En una muestra de 460 empleos, 207 tenían salarios inadecuados.Pruebe la afirmación de que la proporción de empleos con salarios inadecuados es mayor a 0.33. Dejar\(\alpha =\) 0.01.
\(H_0\)\(H_1\)
Prueba de sustitución de fórmulas Valor estadístico valor p
Calculadora:
Test Statistic value valor p
¿Cuál es el intervalo de confianza del 90% para la proporción de empleos con salarios inadecuados?
Margen de sustitución de fórmula del intervalo de confianza de
Intervalo de confianza de la calculadora: __________________
3. Supongamos que tenías dos formas diferentes de llegar a la escuela. Un camino estaba en vías principales con muchos semáforos, el otro camino fue en carreteras secundarias con pocos semáforos. Te gustaría saber cuál es el camino más rápido. Selecciona al azar 6 días para usar la carretera principal y 6 días para usar las carreteras secundarias. Tu objetivo es determinar si el tiempo medio que tarda en la carretera secundaria μb es diferente al tiempo medio en la carretera principal μm. Los datos se presentan en la siguiente tabla. Las unidades son minutos. Supongamos que las variaciones poblacionales son iguales. Debido a que el tamaño de la muestra es pequeño, decideusar un nivel de significancia de\(\alpha = 0.1\).
| Carretera Trasera | 14.5 | 15.0 | 16.2 | 18.9 | 21.3 | 17.4 |
| Carretera Principal | 19.5 | 17.3 | 21.2 | 20.9 | 21.1 | 17.7 |
Escribir las hipótesis nulas y alternativas apropiadas: H0: _____________ H1:______________
¿Cuál es la media de la muestra para cada ruta? Carretera Trasera__________ Carretera Principal ______
¿Cuál es la desviación estándar de la muestra para cada ruta? Carretera Trasera__________ Carretera Principal ______
Prueba esto usando tu calculadora
Test Statistic value valor p
Hay _____________ una diferencia significativa entre tomar la carretera trasera y la carretera principal (t = ______, p = ___________, n=_______).
¿Cuál es el intervalo de confianza del 99% para la diferencia en los tiempos medios?
Intervalo de confianza de la calculadora: __________________
Utilice el intervalo de confianza generado por su calculadora para calcular el margen de error ____________
4. Algunos padres de atletas de grupos de edad creen que su hijo será mejor si les pagan una recompensa económica por tener éxito. Por ejemplo, pueden pagar $5 por anotar un gol en el fútbol o $1 por un mejor momento en un encuentro de natación. El argumento en contra de pagar es que es contraproducente y destruye la automotivación del niño. ¿La tasa de deserción escolar de los niños que han sido pagados es diferente a la de los niños a los que no se les ha pagado? Vamos\(\alpha = 0.05\).
Tasa de deserción escolar de niños que han sido pagados: 450 de 510 Tasa de
deserción escolar de niños que no han sido pagados: 780 de 930
\(H_0\)\(H_1\)
Prueba esto usando tu calculadora
Test Statistic value valor p
¿Cuál es el intervalo de confianza del 95% para la diferencia entre la tasa de deserción escolar de los niños que han sido pagados y los niños que no han sido pagados? Dejar α = 0.05.
Intervalo de confianza de la calculadora: __________________
Utilice el intervalo de confianza generado por su calculadora para calcular el margen de error ____________
Capítulo 7 — Análisis de Regresión Lineal
El problema de la tarea 4 analiza la relación entre la población de una zona metropolitana y el número de patentes producidas en esa zona. A continuación se muestra una muestra expandida. Incluye más de las grandes áreas metropolitanas. Haz una nueva gráfica de dispersión. Use un marcador de color diferente para Indicar Las Vegas y Fresno en este diagrama de dispersión. En la tarea, estas dos comunidades parecían valores atípicos. ¿Todavía?
Utilizar un nivel de significancia del 5%.
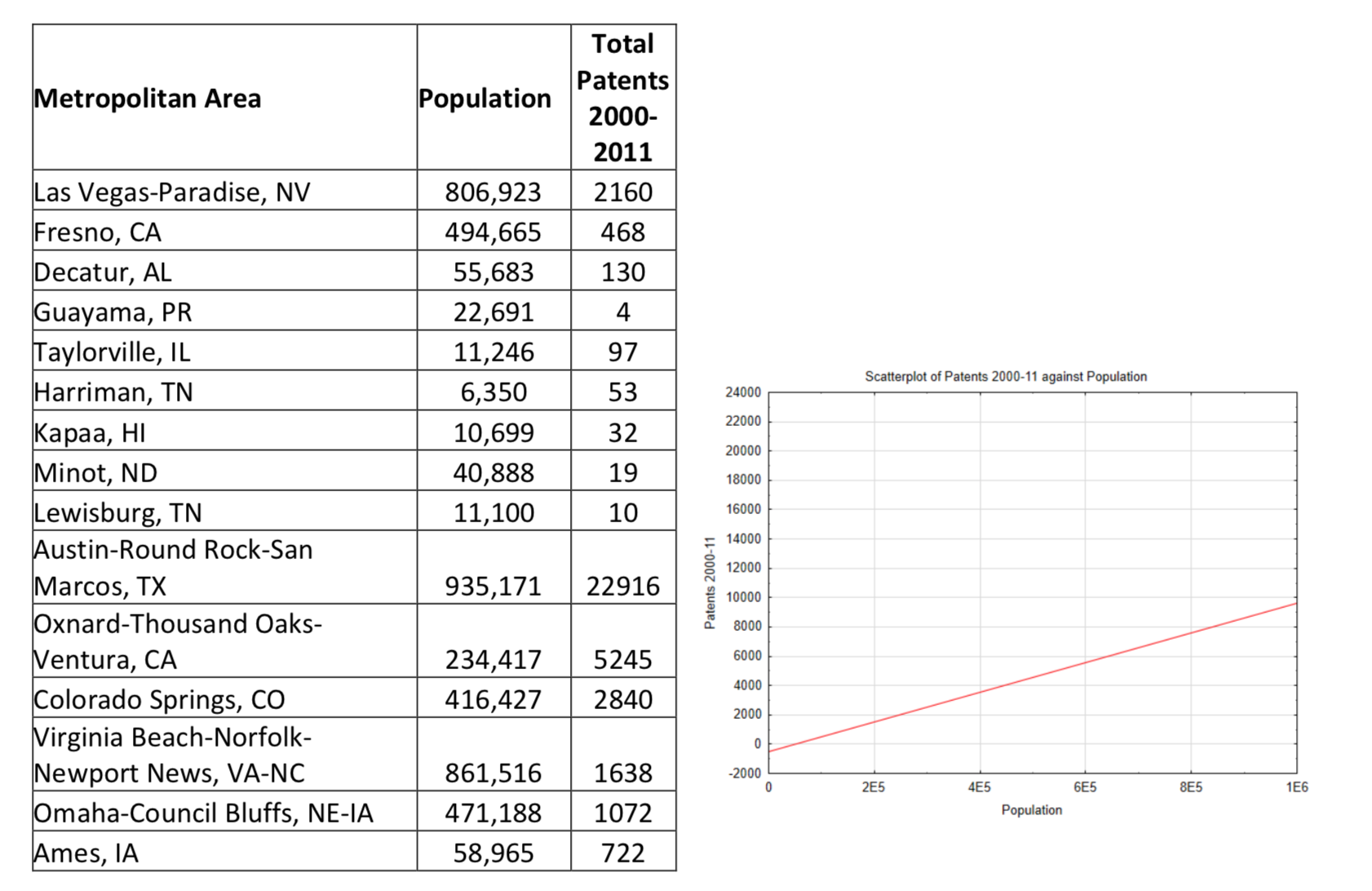
Muestre los resultados de la calculadora incluyendo la correlación, el\(r^2\) valor y la ecuación de la línea de regresión (que ha sido convenientemente colocada en la gráfica para usted). Escribir una conclusión estadística y luego interpretar los resultados. Utilizar un nivel de significancia de 0.10.
Correlación ____________
Coeficiente de determinación (\(r^2\)valor) _______________
Ecuación de regresión _____________________
Prueba de hipótesis frase conclusiva:
Capítulo 7 —\(\chi ^2\)
Si un profesor cambia la forma en que se imparte un curso o utiliza un nuevo libro, ¿cómo sabe el maestro si los cambios resultaron en un mejor éxito para los alumnos? Una forma es comparar la distribución de las calificaciones (A, B, C, por debajo de C) con lo ocurrido en clases pasadas, asumiendo que las evaluaciones y calificaciones fueron similares.
La distribución de las calificaciones para las clases pasadas que utilizaron la primera edición de Fundamentos en el Razonamiento Estadístico se muestra en la columna central de la tabla siguiente. A continuación se muestra el número de alumnos que recibieron cada grado al utilizar la segunda edición.
|
Grado |
Contar a partir de la segunda edición |
|
|
A |
0.349 |
16 |
|
B |
0.287 |
11 |
|
C |
0.204 |
7 |
|
Debajo de C |
0.160 |
6 |
Pruebe la hipótesis de que la distribución de las calificaciones de la segunda edición es diferente a la distribución de la primera edición.
Escribe las hipótesis:
\(H_0\):
\(H_1\):
¿Qué prueba es apropiada para este problema?
A. _______ Bondad de Ajuste B. _______ Prueba de Independencia C. _______ Prueba de Homogeneidad
Pruebe la hipótesis usando la siguiente tabla.
| Observado | Esperado | \(O - E\) | \((O - E)^2\) | \(\dfrac{(O - E)^2}{E}\) |
| \(\chi^2 =\) |
Escribe una oración conclusiva:
¿Cuál de las siguientes conclusiones sustenta la evidencia?
_____La segunda edición resultó en una distribución significativamente mejorada de las calificaciones
_____La segunda edición resultó en un empeoramiento significativo de la distribución de calificaciones
_____La segunda edición no pareció afectar la distribución de las calificaciones
Este problema se podría hacer de una manera diferente si te dijeran el número de personas que obtuvieron cada calificación usando la primera edición.
|
Grado |
Contar desde la primera edición |
Contar a partir de la segunda edición |
A |
174 |
16 |
|
B |
143 |
11 |
|
C |
102 |
7 |
|
Debajo de C |
80 |
6 |
Pruebe la hipótesis de que la distribución de las calificaciones de la segunda edición es diferente a la distribución de la primera edición.
Escribe las hipótesis:
\(H_0:\)
\(H_1:\)
¿Qué prueba es apropiada para este problema?
A. _______ Bondad de Ajuste B. _______ Prueba de Independencia C. _______ Prueba de Homogeneidad
Usa la matriz y\(\chi^2\) prueba en tu calculadora para probar la hipótesis.