4.3: Variables aleatorias

Definición y Primeros Ejemplos

Supongamos que estamos haciendo un experimento aleatorio y hay alguna consecuencia del resultado en el que nos interesa que se puede medir por un número. El experimento podría estar jugando un juego de azar y el resultado podría ser cuánto ganas o pierdes dependiendo del resultado, o el experimento podría ser qué parte del manual de las unidades eliges estudiar aleatoriamente y el resultado cuántos puntos obtenemos en la prueba de licencia de conducir hacemos al día siguiente, o el experimento podría estar dando un nuevo medicamento a un paciente al azar en estudio médico y el resultado sería alguna medida médica que hagas después del tratamiento (presión arterial, recuento de glóbulos blancos, lo que sea), etc. Hay un nombre para esta situación en matemáticas

DEFINICIÓN 4.3.1. La elección de un número para cada resultado de un experimento aleatorio se denomina variable aleatoria [RV]. Si se pueden contar los valores que toma un RV, porque son finitos o contablemente infinitos ⁸ en número, el RV se llama discreto; si, en cambio, el RV toma todos los valores en un intervalo de números reales, el RV se llama continuo.

Usualmente usamos letras mayúsculas para denotar RV y la letra minúscula correspondiente para indicar un valor numérico particular que el RV podría tener, como\(X\) y\(x\).

EJEMPLO 4.3.2. Supongamos que jugamos a un juego tonto donde me pagas 5 dólares por jugar, luego le doy una moneda justa y te doy 10 dólares si la moneda sube de cabeza y 0 dólares si sale de cola. Entonces tus ganancias netas, que serían +$5 o -$5 cada vez que juegues, son una variable aleatoria. Al tener solo dos valores posibles, este RV es ciertamente discreto.

EJEMPLO 4.3.3. Los fenómenos meteorológicos varían tanto, debido a efectos tan pequeños —como la famosa mariposa batiendo sus alas en la selva amazónica provocando un huracán en Norteamérica— que parecen ser un fenómeno aleatorio. Por lo tanto, observar la temperatura en alguna estación meteorológica es una variable aleatoria continua cuyo valor puede ser cualquier número real en algún rango como\(-100\) a\(100\) (estamos haciendo ciencia, entonces usamos\({}^\circ C\)).

EJEMPLO 4.3.4. Supongamos que observamos el experimento de “tirar dos dados justos independientemente” del Ejemplo 4.2.7 y el Ejemplo 4.1.21, que se basó en el modelo de probabilidad en el Ejemplo 4.1.21 y el espacio muestral en el Ejemplo 4.1.4. Consideremos en esta situación la variable aleatoria\(X\) cuyo valor para algún par de tiradas de dados es la suma de los dos números que aparecen en los dados. Entonces, por ejemplo\(X(11)=2\),\(X(12)=3\),, etc.

De hecho, hagamos una tabla de todos los valores de\(X\):\[\begin{aligned} X(11) &= 2\\ X(21) = X(12) &= 3\\ X(31) = X(22) = X(13) &=4\\ X(41) = X(32) = X(23) = X(14) &= 5\\ X(51) = X(42) = X(33) = X(24) = X(15) &= 6\\ X(61) = X(52) = X(43) = X(34) = X(25) = X(16) &= 7\\ X(62) = X(53) = X(44) = X(35) = X(26) &= 8\\ X(63) = X(54) = X(45) = X(36) &= 9\\ X(64) = X(55) = X(46) &= 10\\ X(65) = X(56) &= 11\\ X(66) &= 12\\\end{aligned}\]

Distribuciones para RVs Discretos

Lo primero que hacemos con una variable aleatoria, generalmente, es hablar de las probabilidades asociadas con ella.

DEFINICIÓN 4.3.5. Dado un RV discreto\(X\), su distribución es una lista de todos los valores que\(X\) adquiere, junto con la probabilidad de que tome ese valor.

[Tenga en cuenta que esto es bastante similar a la Definición 1.3.5 — porque es esencialmente lo mismo.]

EJEMPLO 4.3.6. Veamos el RV, al que llamaremos\(X\), en el tonto juego de apuestas del Ejemplo 4.3.2. Como notamos cuando definimos por primera vez ese juego, hay dos valores posibles para este RV, $5 y -$5. De hecho, podemos pensar en “\(X=5\)” como describir un evento, que consiste en el conjunto de todos los resultados del experimento de volteo de monedas que le dan una ganancia neta de $5. Asimismo, “\(X=-5\)” describe el evento que consiste en el conjunto de todos los resultados que le dan una ganancia neta de -$5. Estos eventos son los siguientes:

\(\begin{array}{r|rl}{x} & {\text { Set of outcomes } o} \\ & {\text { such that } X(o)} & {=x} \\ \hline 5 & {\{H\}} \\ {-5} & {\{T\}}\end{array}\)

Al ser una moneda justa por lo que se conocen las probabilidades de estos eventos (y muy simples), concluimos que la distribución de este RV es la tabla

\(\begin{array}{r|rl}{x} & P(X=x) \\ \hline 5 & \ 1/2\ \\ -5 & \ {1/2}\end{array}\)

EJEMPLO 4.3.7. ¿Qué pasa con el\(X=\)"sum of the face values" RV en el experimento aleatorio “tirar dos dados justos, independientemente” del Ejemplo 4.3.4? En realidad ya hemos hecho la mayor parte del trabajo, averiguando qué valores puede tomar el RV y qué resultados causan cada uno de esos valores. Para resumir lo que encontramos:

\(\ \begin{array}{r|ll}{x} & {\text { Set of outcomes } o} \\ & {\text { such that } X(o)}\ {=x} \\ \hline 2 & {\{11\}} \\ {3} & {\{21,12\}} \\ 4 & \{31, 22, 13\}\ \\ 5 & \{41, 32, 23, 14\} \\6 & \{51, 42, 33, 24, 15\}\\7 & \{61, 52, 43, 34, 25, 16\}\\8 & \{62, 53, 44, 35, 26\}\\9 &\{63, 54, 45, 36\} \\10 & \{64, 55, 46\}\\11&\{65, 56\}\\12&\{66\} \end{array}\)

Pero hemos visto que esta es una situación equiprobable, donde está la probabilidad de que cualquier evento\(A\) contenga\(n\) resultados\(P(A)=n\cdot1/36\), así podemos llenar instantáneamente la tabla de distribución para este RV como

\(\ \begin{array}{r|ll}{x} & P(X=x) \\ \hline 2 & \frac{1}{36} \\ {3} & \frac{2}{36} = \frac{1}{18} \\ 4 & \frac{3}{36} = \frac{1}{12} \\ 5 & \frac{4}{36} = \frac{1}{6} \\6 & \frac{5}{36} \\7 & \frac{6}{36} = \frac{1}{6}\\8 & \frac{5}{36}\\9 &\frac{4}{36} = \frac{1}{6} \\10 & \frac{3}{36} = \frac{1}{12}\\11&\frac{2}{36} = \frac{1}{18} \\12 & \frac{1}{36} \end{array}\)

Una cosa a tener en cuenta sobre las distribuciones es que si hacemos una tabla preliminar, como acabamos de hacer, de los eventos consistentes en todos los resultados que dan un valor particular cuando se conectan al RV, entonces tendremos una colección de eventos disjuntos que agota todo el espacio muestral. Lo que esto significa es que la suma de los valores de probabilidad en la tabla de distribución de un RV es la probabilidad de todo el espacio muestral del experimento de ese RV. Por lo tanto

HECHO 4.3.8. La suma de las probabilidades en una tabla de distribución para una variable aleatoria siempre debe ser igual\(1\).

Es bastante buena idea, cada vez que escribes una distribución, verificar que este hecho sea cierto en tu tabla de distribución, simplemente como una comprobación de cordura contra errores aritméticos simples.

Expectativa para vehículos rodantes discretos

Dado que no podemos predecir cuál será exactamente el resultado cada vez que realicemos un experimento aleatorio, no podemos predecir con precisión cuál será el valor de un RV en ese experimento, cada vez. Pero, como hicimos con la idea básica de probabilidad, tal vez al menos podamos aprender algo de las tendencias a largo plazo. Resulta que es relativamente fácil averiguar el valor medio de un RV en un gran número de ejecuciones del experimento.

Decir\(X\) es un RV discreto, para lo cual la distribución nos dice que\(X\) toma los valores\(x_1, \dots, x_n\), cada uno con la probabilidad correspondiente\(p_1, \dots, p_n\). Entonces la visión frecuentista de probabilidad dice que la probabilidad\(p_i\) que\(X=x_i\) es (aproximadamente)\(n_i/N\), donde\(n_i\) está el número de veces\(X=x_i\) fuera de un gran número\(N\) de corridas del experimento. Pero si\[p_i = n_i/N\] entonces, multiplicando ambos lados por\(N\),\[n_i = p_i\,N \ .\] Eso significa que, fuera de las\(N\) corridas del experimento,\(X\) tendrá el valor\(x_1\) en\(p_1\,N\) corridas, el valor\(x_2\) en\(p_2\,N\) corridas, etc. por lo que la suma de\(X\) sobre esas\(N\) corridas será\[(p_1\,N)x_1+(p_2\,N)x_2 + \dots + (p_n\,N)x_n\ .\] Por lo tanto el valor medio de\(X\) sobre estas\(N\) corridas será el total dividido por \(N\), que es\(p_1\,x_1 + \dots + p_n x_n\). Esto motiva la definición

DEFINICIÓN 4.3.9. Dado un RV discreto\(X\) que toma los valores\(x_1, \dots, x_n\) con probabilidades\(p_1, \dots, p_n\), la expectativa [a veces también llamado el valor esperado] de\(X\) es el valor\[E(X) = \sum p_i\,x_i\ .\]

Por lo que vimos justo antes de esta definición, tenemos lo siguiente

HECHO 4.3.10. La expectativa de un RV discreto es la media de sus valores en muchas series del experimento.

Nota: El lector atento habrá notado que nos ocupamos anteriormente solo del caso de un RV finito, no del caso de uno contablemente infinito. Resulta que todo lo anterior funciona bastante bien en ese caso más complejo también, siempre y cuando uno se sienta cómodo con un poco de tecnología matemática llamada “sumando una serie infinita”. No asumimos tal nivel de comodidad en nuestros lectores en este momento, por lo que pasaremos por alto los detalles de las expectativas de los RV infinitos y discretos.

EJEMPLO 4.3.11. Calculemos la expectativa de ganancia neta RV\(X\) en el tonto juego de apuestas del Ejemplo 4.3.2, cuya distribución calculamos en el Ejemplo 4.3.6. Conectando directamente a la definición, vemos\[E(X)=\sum p_i\,x_i = \frac12\cdot5 + \frac12\cdot(-5)=2.5-2.5 = 0 \ .\] En otras palabras, tu ganancia neta promedio jugando a este tonto juego muchas veces será cero. Tenga en cuenta que no significa nada como “si pierdes suficientes veces seguidas, las posibilidades de comenzar a ganar de nuevo subirán”, como muchos jugadores parecen creer, solo significa que, a la larga, podemos esperar que las ganancias promedio sean aproximadamente cero, pero nadie sabe cómo larga esa carrera tiene que ser antes de que ocurra el equilibrio de victorias y derrotas ⁹.

Un ejemplo más interesante es

EJEMPLO 4.3.12. En el Ejemplo 4.3.7 calculamos la distribución de la variable aleatoria\(X=\) "sum of the face values" en el experimento aleatorio “tirar dos dados justos, independientemente” del Ejemplo 4.3.4. Por lo tanto, es fácil tapar los valores de las probabilidades y los valores RV de la tabla de distribución en la fórmula para la expectativa, para obtener\[\begin{aligned} E(X) &=\sum p_i\,x_i\\ &= \frac1{36}\cdot2 + \frac2{36}\cdot3 + \frac3{36}\cdot4 + \frac4{36}\cdot5 + \frac5{36}\cdot6 + \frac6{36}\cdot7 + \frac5{36}\cdot8 + \frac4{36}\cdot9 + \frac3{36}\cdot10\\ &\hphantom{= \frac1{36}\cdot2 + \frac2{36}\cdot3 + \frac3{36}\cdot4 + \frac4{36}\cdot5 + \frac5{36}\cdot6 + \frac6{36}\cdot7 + \frac5{36}\cdot8\ } + \frac2{36}\cdot11 + \frac1{36}\cdot12\\ &= \frac{2\cdot1 + 3\cdot2 + 4\cdot3 + 5\cdot4 + 6\cdot5 + 7\cdot6 + 8\cdot5 + 9\cdot4 + 10\cdot3 + 11\cdot2 + 12\cdot1}{36}\\ &= 7\end{aligned}\] Así que si tiras dos dados justos de forma independiente y sumas los números que surgen, entonces haz este proceso muchas veces y toma el promedio, a la larga que promedio será el valor\(7\).

Funciones de densidad para vehículos rodantes continuos

¿Qué pasa con las variables aleatorias continuas? La definición 4.3.5 de distribución excluía explícitamente el caso de las RV continuas, entonces ¿significa eso que no podemos hacer cálculos de probabilidad en ese caso?

Hay, cuando lo pensamos, algo así como un problema aquí. Se supone que una distribución es una lista de posibles valores del RV y la probabilidad de cada uno de esos valores. Pero si alguna RV continua tiene valores que son un intervalo de números reales, simplemente no hay forma de enumerar todos esos números —se sabe desde finales del siglo XIX que no hay forma de hacer una lista como esa (ver, para una descripción de una muy bonita prueba de este hecho). Además, la posibilidad de que algún proceso aleatorio produzca un número real que sea exactamente igual a algún valor en particular es realmente cero: para que dos números reales sean exactamente iguales requiere una precisión infinita... piensa en todos esos dígitos decimales, marchando en filas ordenadas hasta el infinito , que debe coincidir entre los dos números.

En lugar de una distribución, hacemos lo siguiente:

DEFINICIÓN 4.3.13. Dejar\(X\) ser una variable aleatoria continua cuyos valores son el intervalo real\([x_{min},x_{max}]\), donde cualquiera\(x_{min}\)\(x_{max}\) o ambos pueden estar\(\infty\). Una función de densidad [probabilidad] para\(X\) es una función\(f(x)\) definida para\(x\) in\([x_{min},x_{max}]\), lo que significa que es una curva con un\(y\) valor para cada \(x\)en ese intervalo, con la propiedad que\[P(a<X<b) = \left\{\begin{matrix}\text{the area in the xy-plane above the x-axis, below}\\ \text{the curve y=f(x) and between x=a and x=b.}\end{matrix}\right.\ .\]

Gráficamente, lo que está pasando aquí es

Por lo que sabemos de probabilidades, lo siguiente es cierto (y bastante fácil de probar):

HECHO 4.3.14. Supongamos que\(f(x)\) es una función de densidad para el RV continuo\(X\) definido en el intervalo real\([x_{min},x_{max}]\). Entonces

• Para todos\(x\) en\([x_{min},x_{max}]\),\(f(x)\ge0\).
• El área total bajo la curva\(y=f(x)\), por encima del\(x\) eje -y entre\(x=x_{min}\) y\(x=x_{max}\) es\(1\).

Si queremos la idea de escoger un número real en el intervalo al azar, donde\([x_{min},x_{max}]\) al azar significa que todos los números tienen la misma posibilidad de ser escogidos (a lo largo de las líneas de feria en Definición 4.1.20, la altura de la función de densidad debe ser la misma en absoluto\(x\). En otras palabras, la función de densidad\(f(x)\) debe ser una constante\(c\). De hecho, por el hecho anterior 4.3.14, esa constante debe tener el valor\(\frac1{x_{max}-x_{min}}\). Hay un nombre para esto:

DEFINICIÓN 4.3.15. La distribución uniforme on \([x_{min},x_{max}]\)es la distribución para el RV continuo cuyos valores son el intervalo\([x_{min},x_{max}]\) y cuya función de densidad es la función constante\(f(x)=\frac1{x_{max}-x_{min}}\).

EJEMPLO 4.3.16. Supongamos que tomas un autobús a la escuela todos los días y debido a una caótica vida hogareña (y, seamos sinceros, no te gustan las mañanas), llegas a la parada del autobús a una hora casi perfectamente aleatoria. El autobús tampoco se ajusta perfectamente a su horario, pero está garantizado que llegará al menos cada\(30\) minuto. A lo que esto suma es la idea de que su tiempo de espera en la parada del autobús es un RV distribuido uniformemente en el intervalo\([0,30]\).

Si alguna mañana te preguntas qué tan probable es entonces que esperes menos de\(10\) minutos, simplemente puedes calcular el área del rectángulo cuya base es el intervalo\([0,10]\) en el\(x\) eje -y cuya altura es\(\frac1{30}\), que será \[P(0<X<10)=base \cdot height =10\cdot\frac1{30}=\frac13\ .\]Una imagen que debería aclarar esto es

donde el área de la región sombreada representa la probabilidad de tener un tiempo de espera de\(0\) a\(10\) minutos.

Una cosa técnica que puede resultar confusa sobre los RV continuos y sus funciones de densidad es la cuestión de si debemos escribir\(P(a<X<b)\) o\(P(a\le X\le b)\). Pero si lo piensas, realmente tenemos tres eventos posibles aquí:\[\begin{aligned} A &= \{\text{outcomes such that } X=a\},\\ M &= \{\text{ outcomes such that $a<X<b$}\},\text{and}\\ B &= \{\text{ outcomes such that $X=b$}\}\ .\end{aligned}\] Dado que\(X\) siempre adquiere exactamente un valor para cualquier resultado en particular, no hay superposición entre estos eventos: todos son disjuntos. Eso quiere decir que\[P(A\cup M\cup B) = P(A)+P(M)+P(B) = P(M)\] donde está la última igualdad porque, como dijimos anteriormente, la probabilidad de que un RV continuo asuma exactamente un valor particular, como lo haría en los eventos\(A\) y\(B\), es\(0\). Lo mismo sería cierto si agregáramos simplemente un punto final del intervalo\((a,b)\). Para resumir:

HECHO 4.3.17. Si\(X\) es un RV continuo con valores que forman el intervalo\([x_{min},x_{max}]\) y\(a\) y\(b\) están en este intervalo, entonces\[P(a<X<b) = P(a<X\le b) = P(a\le X<b) = P(a\le X\le b)\ .\]

Como consecuencia de este hecho, algunos autores escriben probabilidad formul æ sobre RV continuas con “\({}<{}\)” y algunos con “\({}\le{}\)” y no hace ninguna diferencia.

Hagamos un ejemplo un poco más interesante que la distribución uniforme:

EJEMPLO 4.3.18. Supongamos que lanzas repetidamente dardos a una dardos. No eres una máquina, así que los dardos golpean en diferentes lugares cada vez y piensas en esto como un experimento aleatorio repetible cuyos resultados son las ubicaciones del dardo en el tablero. Te interesan las probabilidades de acercarte al centro del tablero, así que decides por cada resultado experimental (ubicación de un dardo que lanzaste) medir su distancia al centro — este será tu RV\(X\).

Al ser bueno en este juego, golpeas cerca del centro más que cerca del borde y nunca pierdes por completo el tablero, cuyo radio es\(10cm\) — por lo que\(X\) es más probable que esté cerca\(0\) que cerca\(10\), y nunca es mayor que \(10\). Lo que esto significa es que el RV tiene valores que forman el intervalo\([0,10]\) y la función de densidad, definida en el mismo intervalo, debe tener su valor máximo en\(x=0\) y debe bajar al valor\(0\) cuando\(x=10\).

Usted decide modelar esta situación con la función de densidad más simple que se le ocurra que tiene las propiedades que acabamos de notar: una línea recta desde el punto más alto de la función de densidad cuando\(x=0\) hacia abajo hasta el punto\((10,0)\). La cifra que resultará será un triángulo, y dado que el área total debe ser\(1\) y la base es\(10\) unidades de largo, la altura debe ser\(.2\) unidades. [Para conseguirlo, resolvimos la ecuación\(1=\frac12bh=\frac1210h=5h\) para\(h\).] Entonces la gráfica debe ser

y la ecuación de esta función de densidad lineal sería\(y=-\frac1{50}x+.2\) [¿por qué? — pensar en la pendiente y\(y\) -interceptar!].

En la medida en que confíes en este modelo, ahora puedes calcular las probabilidades de eventos como, por ejemplo, “golpear el tablero dentro de ese centro de ojo de buey de radio” \(1.5cm\), cuya probabilidad sería el área de la región sombreada en esta gráfica:

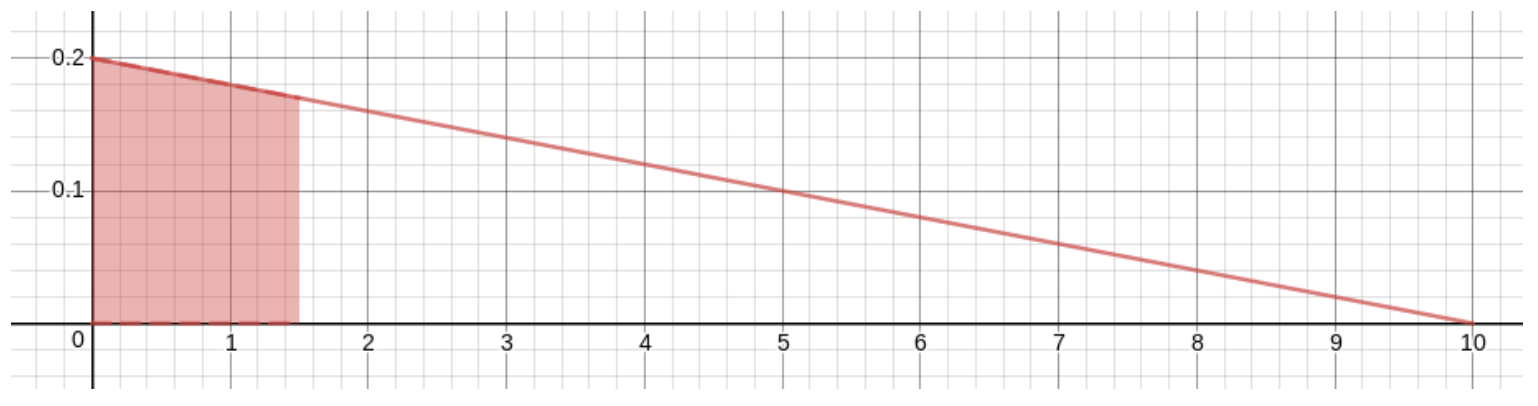
La esquina superior derecha de esta región sombreada está en\(x\) -coordenada\(1.5\) y está en la línea, por lo que su\(y\) coordenada es\(-\frac1{50}1.5+.2=.17\). Dado que la región es un trapecio, su área es la distancia entre los dos lados paralelos multiplicada por el promedio de las longitudes de los otros dos lados, dando\[P(0<X<1.5) = 1.5\cdot\frac{.2+.17}2 = .2775\ .\] En otras palabras, la probabilidad de golpear el ojo de buey, asumiendo este modelo de tu destreza para lanzar dardos, es de aproximadamente\(28\)%.

Si no recuerdas la fórmula para el área de un trapecio, puedes hacer este problema de otra manera: computar la probabilidad del evento complementario, y luego tomar uno menos ese número. La razón para hacer esto sería que el evento complementario corresponde a la región sombreada aquí

que es un triángulo! Ya que seguramente sí recordamos la fórmula para el área de un triángulo, nos encontramos con eso\[P(1.5<X<10)=\frac12bh=\frac{1}{2}.17\cdot8.5=.7225\] y por lo tanto\(P(0<X<1.5)=1-P(1.5<X<10)=1-.7225=.2775\). [¡Es bueno que también tengamos el mismo número de esta manera!]

La distribución normal

Hemos visto algunos ejemplos de RVs continuos, pero aún tenemos que cumplir con el más importante de todos.

DEFINICIÓN 4.3.19. La distribución Normal con media\(\ \mu X\) y desviación estándar\(\ \sigma X\) es la RV continua que toma todos los valores reales y se rige por la función de densidad de probabilidad\[\rho(x)=\frac1{\sqrt{2 \sigma X^2\pi}}e^{-\frac{(x- \mu X)^2}{2 \sigma X^2}}\ .\] If\(X\) es aleatoria variable que sigue esta distribución, entonces decimos que\(X\) se distribuye normalmente con media\(\ \mu X\) y desviación estándar\(\ \sigma X\) o, en símbolos,\(X\) es\(N(\ \mu X, \sigma X)\).

[Obras más técnicas también llaman a esto la distribución gaussiana, que lleva el nombre del gran matemático Carl Friedrich Gauss. Pero no volveremos a usar ese término en este libro después de que termine esta oración.]

La buena noticia de esta complicada fórmula es que en realidad no tenemos que hacer nada con ella. Recopilaremos algunas propiedades de la distribución Normal que se han derivado de esta fórmula, pero estas propiedades son lo suficientemente útiles, y otras herramientas como calculadoras modernas y computadoras que pueden encontrar áreas específicas que necesitamos bajo la gráfica de\(y=\rho(x)\), que no necesitaremos trabajar directamente con la fórmula anterior para\(\rho(x)\) otra vez. Es bueno saber que\(N(\mu X, \sigma X)\) sí corresponde a una función de densidad específica, conocida, ¿no es así?

Ayuda comenzar con una imagen de cómo se ve la distribución Normal. Aquí está la función de densidad para\(\mu X=17\) y\(\sigma X=3\):

Ahora vamos a recopilar algunos de estos datos útiles sobre las distribuciones normales.

HECHO 4.3.20. La función de densidad ρ para la distribución Normal N (μ _X, σ _X) es una función positiva para todos los valores de x y el área total bajo la curva y = ρ (x) es 1.

Esto simplemente significa que ρ es un buen candidato para la función de densidad de probabilidad para algún RV continuo.

HECHO 4.3.21. La función de densidad ρ para la distribución Normal N (μ _X, σ _X) es unimodal con máximo en la coordenada _x μ X.

Esto significa que N (μ _X, σ _X) es un posible modelo para un RV X que tiende a tener un valor principal, central, y menos a menudo tiene otros valores más alejados. Ese centro está en la ubicación dada por el parámetro μ _X, así que donde quiera que queramos poner el centro de nuestro modelo para X, solo usamos eso para μ _X.

HECHO 4.3.22. La función de densidad ρ para la distribución Normal N (μ _X, σ _X) es simétrica cuando se refleja a través de la línea x = μ _X.

Esto significa que la cantidad X pierde su centro, μ _X, tiende a ser aproximadamente la misma cuando pierde por encima de μ _X y cuando falla por debajo de μ _X. Esto correspondería a situaciones en las que golpearas tanto a la derecha como a la izquierda del centro de una dianas. O cuando se escogen al azar, las personas son tan propensas a ser más altas que la estatura promedio como a ser más bajas. O cuando el tiempo que tarda un estudiante en terminar una prueba estandarizada es tan probable que sea menor que el promedio como sea más que el promedio. O en muchas, muchas otras situaciones útiles.

HECHO 4.3.23. La función de densidad ρ para la distribución Normal N (μ _{X, σ X}) tiene colas en ambas direcciones que son bastante delgadas, de hecho se vuelven extremadamente delgadas como x → ±∞, pero nunca van hasta 0.

Esto significa que N (μ _X, σ _X) modela situaciones donde la cantidad X se desvía de su promedio no tiene un corte particular en la dirección positiva o negativa. Entonces estás lanzando dardos a un tablero de dardos, por ejemplo, y no hay forma de saber hasta dónde puede golpear tu dardo a la derecha o a la izquierda del centro, tal vez incluso muy lejos del tablero y al final del pasillo —aunque eso puede ser muy poco probable. O tal vez el tiempo que lleva completar alguna tarea suele ser cierta cantidad, pero de vez en cuando puede llevar mucho más tiempo, tanto más que realmente no hay un límite natural que quizás conozcas con anticipación.

Al mismo tiempo, esas colas de la distribución Normal son tan delgadas, para valores alejados de μ _X, que puede ser un buen modelo incluso para una situación en la que hay un límite natural a los valores de X por encima o por debajo de μ _X. Por ejemplo, las alturas de los machos adultos (en pulgadas) en Estados Unidos están bastante bien aproximadas por N (69,2.8), aunque las alturas nunca pueden ser inferiores a 0 y N (69, 2.8) tiene una cola infinitamente larga a la izquierda —porque si bien esa cola es distinta de cero hasta el final como x → −∞, es muy, muy delgada.

Todos los hechos anteriores son claramente ciertos en la primera gráfica que vimos de una función de densidad de distribución Normal.

HECHO 4.3.24. La gráfica de la función de densidad ρ para la distribución Normal N (μ _X, σ _X) tiene un pico más alto y más estrecho si σX es menor, y un pico más bajo y más ancho si σX es mayor.

Esto permite al estadístico ajustar cuánta variación suele haber en un RV normalmente distribuido: Al hacer σX pequeña, estamos diciendo que un RV X que es N (μ _{X, σ X}) es muy probable que tenga valores bastante cercanos a su centro, μ _X. Sin embargo, si hacemos σX grande, es más probable que X tenga valores por todas partes, todavía, centrado en μ _X, pero es más probable que se desplace más lejos.

Hagamos algunas versiones de la gráfica que vimos para ρ cuando μ _X tenía 17 y σX era 3, pero ahora con diferentes valores de σ _X. Primero, si σ _X = 1, obtenemos

Si, en cambio, σ _X = 5, entonces obtenemos

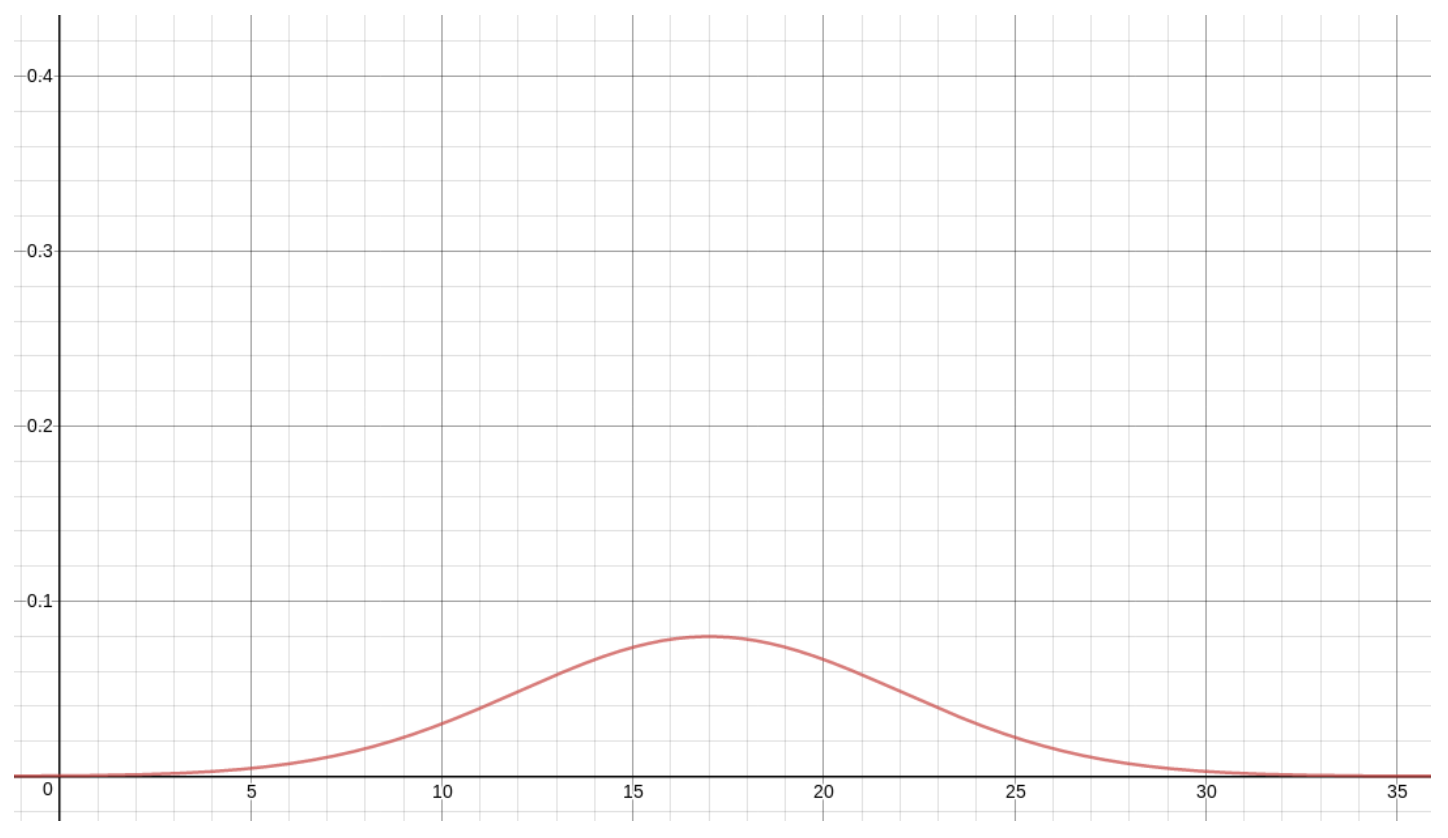
Finalmente, superpongamos todas las funciones de densidad anteriores entre sí, para una gráfica combinada:

Esta variedad de distribuciones Normal (una por cada μ _X y σ _X) es un poco desconcertante, así que tradicionalmente, nos concentramos en una particularmente agradable.

DEFINICIÓN 4.3.25. La distribución Normal con media μ _X = 0 y desviación estándar σ _X = 1 se denomina distribución Normal estándar y una RV [a menudo escrita con la variable Z] que es N (0, 1) se describe como una RV Normal estándar. Aquí está lo que la Normal estándar función de densidad de probabilidad se ve así:

Así es como se ve la función de densidad de probabilidad normal estándar:

Una cosa buena del estándar Normal es que todas las demás distribuciones normales pueden estar relacionadas con el estándar.

HECHO 4.3.26. Si X es N (μ _X, σ _X), entonces Z = (X−μ _X) /σ _X es Normal estándar.

Esto tiene nombre.

DEFINICIÓN 4.3.27. El proceso de reemplazar una variable aleatoria X que es N (μ _X, σ _X) por la RV normal estándar Z = (X − μ _X) /σ _X se llama estandarizar un RV Normal.

Solía ser que la estandarización era un paso importante en la resolución de problemas con RV Normales. Se plantearía un problema con la información sobre algunos datos que fueron modelados por un RV Normal con media dada μ _X y estandarización σ _X. Luego, las preguntas sobre las probabilidades para esos datos podrían responderse estandarizando el RV y buscando valores en una sola tabla de áreas bajo la curva normal estándar.

Hoy en día, con herramientas electrónicas como calculadoras estadísticas y computadoras, el paso de estandarización no es realmente necesario.

EJEMPLO 4.3.28. Como señalamos anteriormente, las alturas de los hombres adultos en Estados Unidos, cuando se miden en pulgadas, dan un RV\(X\) que es\(N(69, 2.8)\). ¿Qué porcentaje de la población, entonces, es más alto que\(6\) los pies?

En primer lugar, el punto de vista frecuentista sobre la probabilidad nos dice que lo que nos interesa es la probabilidad de que un macho americano adulto elegido al azar sea más alto de 6 pies —eso será lo mismo que el porcentaje de la población tan alta. Es decir, debemos encontrar la probabilidad de que X > 72, ya que en pulgadas, 6 pies se convierte en 72. Como X es un RV continuo, debemos encontrar el área bajo su curva de densidad, que es la ρ para N (69, 2.8), entre 72 y ∞.

Eso ∞ es un poco intimidante, pero como las colas de la distribución Normal son muy delgadas, podemos dejar de medir área cuando x es algún número grande y habremos perdido solo una cantidad muy pequeña de área, por lo que tendremos una muy buena aproximación. Por lo tanto, encontremos el área debajo de ρ desde x = 72 hasta x = 1000. Esto se puede hacer de muchas maneras:

• Con una amplia gama de herramientas en línea, solo busque “calculadora de probabilidad normal en línea”. Uno de estos arroja el valor .142.
• Con una calculadora Ti-8x, escribiendo

  normalcdf (72, 1000, 69, 2.8)

  lo que arroja el valor .1419884174. La sintaxis general aquí es

  normalcdf (a, b, μ _X, σ _X)

  para encontrar P (a < X < b) cuando X es N (μ _X, σ _X). Tenga en cuenta que obtiene normalcdf escribiendo

  

• Hojas de cálculo como LibreOffice Calc y Microsoft Excel calcularán esto poniendo lo siguiente en una celda

  =1-NORM.DIST (72, 69, 2.8, 1)

  dando el valor 0.1419883859. Aquí estamos usando el comando

  NORM.DIST (b, μ _X, σ _X, 1)

  que calcula el área bajo la función de densidad para N (μ _X, σ _X) de −∞ a b. [La última entrada de “1” a NORM.DIST simplemente le dice que queremos calcular el área bajo la curva. Si en su lugar usáramos “0”, simplemente nos diría el valor particular de ρ (b), que es de muy poca utilidad en los cálculos de probabilidad.] Por lo tanto, al hacer 1 − NORM.DIST (72,69,2.8,1), estamos tomando el área total de 1 y restando el área a la izquierda de 72, cediendo el área a la derecha, como queríamos.

  Por lo tanto, si quieres el área entre a y b en un RV N (μ _X, σ _X) usando una hoja de cálculo, pondrías

  =DISTR.NORM (b, μX, σX, 1) - NORM.DIST (a, μX, σX, 1)

  en una celda.

Si bien estandarizar un RV Normal no estándar y luego buscar valores en una tabla es un método anticuado que es tedioso y ya no es realmente necesario, una técnica antigua todavía es útil algunas veces. Se basa en lo siguiente:

HECHO 4.3.29. El 68-95-99.7 Regla: Que X sea un N (μ _X, σ _X) RV. Entonces es bueno saber algunos valores especiales del área bajo la gráfica de la curva de densidad ρ para X:

• El área bajo la gráfica de ρ de x=μ _X −σ _X a x=μ _X +σ _X, también conocida como P (μ _X −σ _X <X<μ _X +σ _X), es .68.
• El área bajo la gráfica de ρ de x=μ _X −2σ _X a x=μ _X +2σ _X, también conocida como P (μ _X −2σ _X <X <μ _X +2σ _X), es .95.
• El área bajo la gráfica de ρ de x=μ _X −3σ _X a x=μ _X +3σ _X, también conocida como P (μ _X −3σ _X <X <μ _X +3σ _X), es .997.

Esto también es llamado La regla empírica por algunos autores. Visualmente ³:

---

³ Por Dan Kernler - Obra propia, CC BY-SA 4.0, commons.wikimedia.org/w/index. php? curid=36506025.

---

Para utilizar la Regla 68-95-99.7 para entender una situación particular, es útil estar atento a los números de los que habla. Por lo tanto, al mirar un problema, uno debería notar si los números μ _X +σ _X, μ _X −σ _X, μ _X +2σ _X, μ _X −2σ _X, μ _X +3σ _X, o μ _X − 3σ _X son alguna vez mencionado. Si es así, tal vez esta Regla pueda ayudar.

EJEMPLO 4.3.30. En el Ejemplo 4.3.28, necesitábamos calcular P (X > 72) donde se sabía que X era N (69,2.8). ¿Es 72 uno de los números que deberíamos estar buscando, para usar la Regla? Bueno, es mayor que μ _X = 69, así que podríamos esperar que fuera μ _X + σ _X, μ _X + 2σ _X, o μ _X + 3σ _X. Pero los valores son

μ _X +σ _X =69+2.8=71.8,

μ _X +2σ _X =69+5.6=74.6, y

μ _X +3σ _X =69+8.4=77.4,

ninguno de los cuales es lo que necesitamos.

Bueno, es cierto que 72 ≈ 71.8, así que podríamos usar ese hecho y aceptar que solo estamos obteniendo una respuesta aproximada —una elección extraña, dada la disponibilidad de herramientas que nos darán respuestas extremadamente precisas, pero vamos a ir con ella por un minuto.

A ver, la Regla anterior nos dice que

P (66.2<X <71.8) =P (μ _X −σ _X <X <μ _X +σ _X) =.68.

Ahora como el área total bajo cualquier curva de densidad es 1,

P (X <66.2orX >71.8) =1−P (66.2<X <71.8) =1−.68=.32.

Dado que el evento “X < 66.2” is disjoint from the event “X > 71.8” (X solo toma un valor a la vez, por lo que no puede ser simultáneamente menor que 66.2 y mayor que 71.8), podemos usar la regla simple para la adición de probabilidades:

.32=P (X <66.2orX >71.8) =P (X71.8 <66.2) +P (X >).

Ahora, dado que la función de densidad de la distribución Normal es simétrica alrededor de la línea x = μ _X, los dos términos a la derecha en la ecuación anterior son iguales, lo que significa que

P (X >71.8) =\(\ \frac{1}{2}\) (P (X71.8 <66.2) +P (X >)) = .32=.16\(\ \frac{1}{2}\).

Podría ayudar a visualizar la simetría aquí como la igualdad de las dos áreas sombreadas en la siguiente gráfica

Ahora bien, usando el hecho de que 72 ≈ 71.8, podemos decir que

P (X > 72) ≈ P (X > 71.8) = .16

que, como sabemos que de hecho P (X > 72) = .1419883859, no es una aproximación del todo terrible.

EJEMPLO 4.3.31. Hagamos un cálculo más en el contexto de las alturas de los machos americanos adultos, como en el inmediatamente anterior Ejemplo 4.3.30, pero ahora uno en el que la Regla 68-95-99.7 da una respuesta más precisa.

Entonces digamos que esta vez nos preguntan qué proporción de hombres estadounidenses adultos son más bajos que 63.4 pulgadas. ¿Por qué esa altura, en particular? Bueno, es lo alto que los arqueólogos han disuadido- minado al Rey Tut era en la vida. [No, eso está maquilado. Es sólo un buen número para este problema.]

Nuevamente, mirando a través de los valores μ _X ± σ _{X, μ X} ± 2σ _X y μ _X ± 3σ _X, notamos que

63.4=69−5.6=μ _X −2σ _X.

Por lo tanto, responder qué fracción de machos americanos adultos son menores de 63.4 pulgadas equivale a preguntar cuál es el valor de P (X < μ _X − 2σ _X).

Lo que sabemos de μ _X ± 2σ _X es que la probabilidad de que X esté entre esos dos valores es P (μ _X − 2σ _X < X < μ _X + 2σ _X) = .95. Como en el Ejemplo anterior, el evento complementario a “μ _X − 2σ _X < X < μ _X + 2σ _X”, que tendrá probabilidad .05, consta de dos piezas “X < μ _X − 2σ _X” y “X > μ _X + 2σ _X”, que tienen la misma área por simetría. Por lo tanto

\(\begin{aligned} P(X<63.4) &=P\left(X<\mu_{X}-2 \sigma_{X}\right) \\ &=\frac{1}{2}\left[P\left(X<\mu_{X}-2 \sigma_{X}\right)+P\left(X>\mu_{X}+2 \sigma_{X}\right)\right] \\ &=\frac{1}{2} P\left(X<\mu_{X}-2 \sigma_{X} \text { or } X>\mu_{X}+2 \sigma_{X}\right) \text { since they're disjoint } \\ &=\frac{1}{2} P\left(\left(\mu_{X}-2 \sigma_{X}<X<\mu_{X}+2 \sigma_{X}\right)^{c}\right) \\ &=\frac{1}{2}\left[1-P\left(\mu_{X}-2 \sigma_{X}<X<\mu_{X}+2 \sigma_{X}\right)^{c}\right) \quad \\ &=\frac{1}{2}\left[1-P\left(\mu_{X}-2 \sigma_{X}<X<\mu_{X}+2 \sigma_{X}\right)^{c}\right) \quad \text { by prob. for complements } \\ &=\frac{1}{2} \cdot 05 \\ &=.025 \end{aligned}\)

Solo la manera de encontrar los valores X particulares μ _X ± σ _X, μ _X ± 2σ _X, y μ _X ± 3σ _X en una situación particular nos diría que la Regla 68-95-99.7 podría ser útil, por lo que también encontraría los valores de probabilidad .68, .95, 99.7, o sus complementa .32, .05, o .003, — o incluso la mitad de uno de esos números, usando la simetría.

EJEMPLO 4.3.32. Continuando con el escenario del Ejemplo 4.3.30, descubramos ahora cuál es la altura por encima de la cual sólo habrá .15% de la población.

Observe que .15%, o la proporción .0015, no es uno de los números en la Regla 68-95-99.7, ni es uno de sus complementos —sino que es la mitad de uno de los complementos, siendo la mitad de .003. Ahora bien, .003 es la probabilidad complementaria a .997, que fue la probabilidad en el rango μ _X ± 3σ _X. Como ya hemos visto (dos veces), el área complementaria a la de la región entre μ _X ± 3σ _X consiste en dos colas delgadas que son de igual área, siendo cada una de estas áreas\(\ \frac{1}{2}\) (1 − .997) = .0015. Todo esto significa que el inicio de esa cola superior, por encima del cual se encuentra el valor .15% de la población, es el valor _{X μ X} +3σ _X =68+3·2.8=77.4.

Por lo tanto, .15% de los machos americanos adultos son más altos que 77.4 pulgadas.