6.2: Principios de Buena Visualización

Se han escrito muchos libros sobre visualización efectiva de datos. Hay algunos principios en los que la mayoría de estos autores coinciden, mientras que otros son más polémicos. Aquí resumimos algunos de los principios principales; si quieres aprender más, entonces algunos buenos recursos se enumeran en la sección Lecturas sugeridas al final de este capítulo.

6.2.1 Mostrar los datos y hacerlos destacar

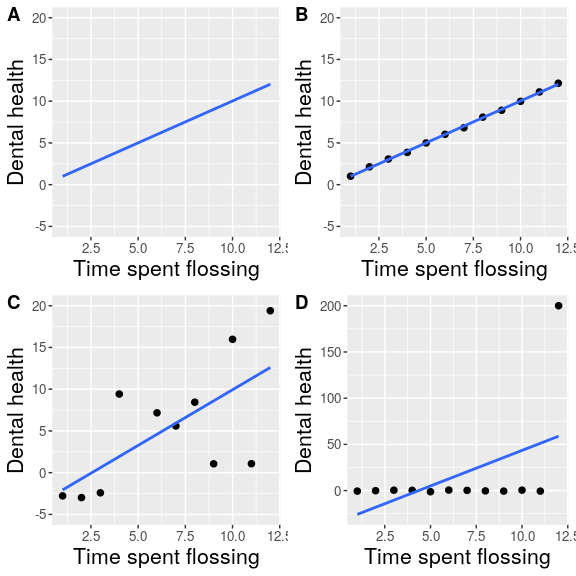
Digamos que había realizado un estudio que examinaba la relación entre la salud dental y el tiempo dedicado a usar hilo dental, y me gustaría visualizar mis datos. La Figura 6.4 muestra cuatro posibles presentaciones de estos datos.

1. En el panel A, en realidad no mostramos los datos, solo una línea que expresa la relación entre los datos. Esto claramente no es óptimo, porque en realidad no podemos ver cómo se ven los datos subyacentes.

Los paneles B-D muestran tres posibles resultados de trazar los datos reales, donde cada gráfica muestra una manera diferente en que los datos podrían haber tenido un aspecto diferente.

2. Si viéramos la trama en el Panel B, probablemente sospecharíamos —raramente los datos reales seguirían un patrón tan preciso.
3. Los datos del Panel C, por otro lado, parecen datos reales —muestran una tendencia general, pero son desordenados, como suelen ser los datos en el mundo.
4. Los datos del Panel D nos muestran que la aparente relación entre las dos variables es causada únicamente por un individuo, al que nos referiríamos como un valor atípico porque caen tan lejos fuera del patrón del resto del grupo. Debe quedar claro que probablemente no queremos concluir mucho a partir de un efecto que es impulsado por un punto de datos. Esta cifra resalta por qué siempre es importante mirar los datos brutos antes de poner demasiada fe en cualquier resumen de los datos.

Figura 6.4: Cuatro posibles presentaciones diferentes de datos para el ejemplo de salud dental. Cada punto en la gráfica de dispersión representa un punto de datos en el conjunto de datos, y la línea en cada gráfica representa la tendencia lineal en los datos.

6.2.2 Maximizar la relación datos/tinta

Edward Tufte ha propuesto una idea llamada relación datos/tinta:

\(\ data/ink\ ratio = {\frac {amount\ of\ ink\ used\ on\ data}{total\ amount\ of\ ink}}\)

$$$$
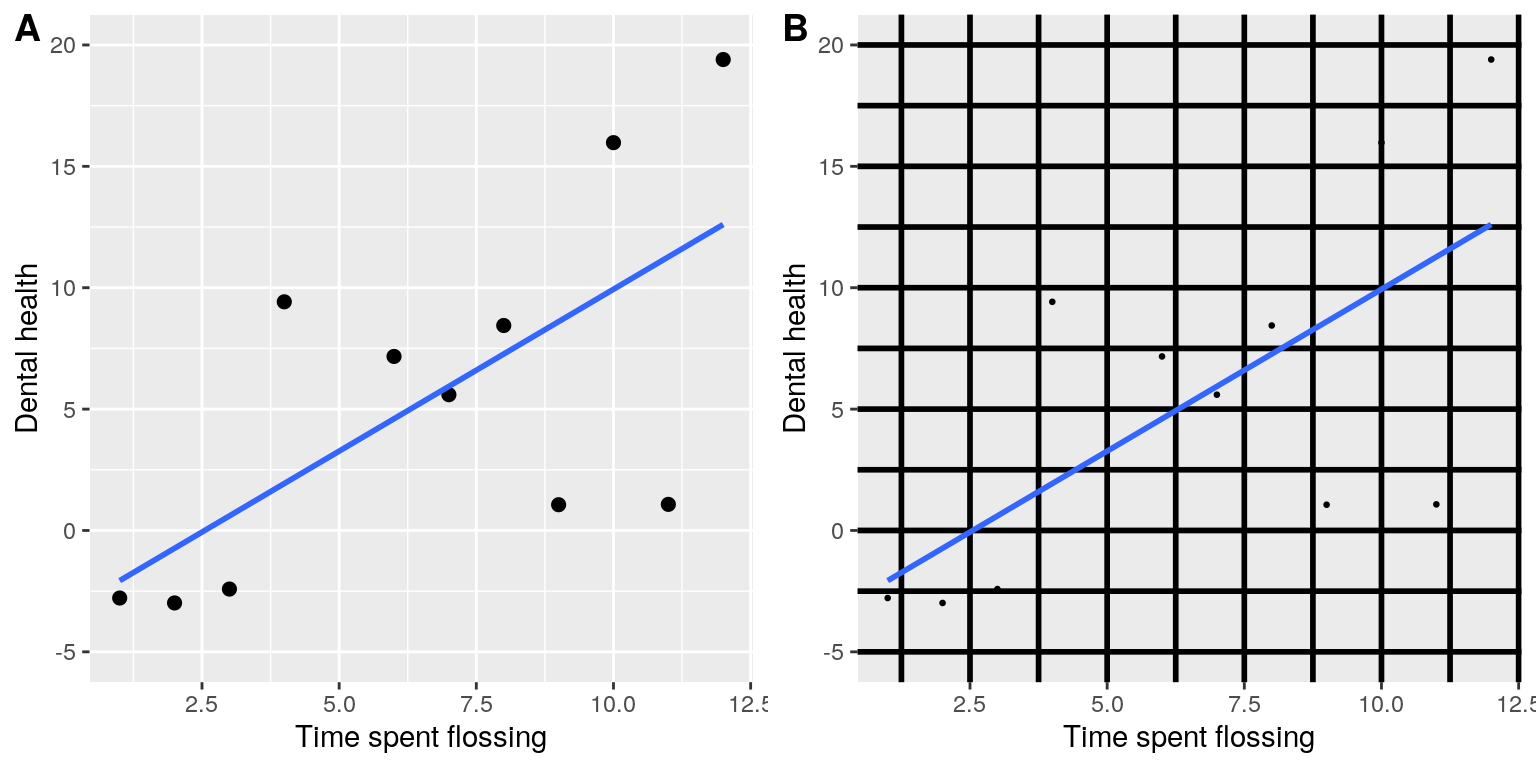
El objetivo de esto es minimizar el desorden visual y dejar que los datos se muestren a través. Por ejemplo, tomemos las dos presentaciones de los datos de salud dental en la Figura 6.5. Ambos paneles muestran los mismos datos, pero el panel A es mucho más fácil de aprehender, debido a su relativamente mayor relación datos/tinta.

Figura 6.5: Un ejemplo de los mismos datos trazados con dos relaciones de datos/tinta diferentes.

6.2.3 Evitar chartjunk

Es especialmente común ver presentaciones de datos en los medios populares que están adornadas con muchos elementos visuales que están temáticamente relacionados con el contenido pero no relacionados con los datos reales. Esto se conoce como chartjunk, y debe evitarse a toda costa.

Una buena manera de evitar chartjunk es evitar usar programas populares de hojas de cálculo para trazar los datos de uno. Por ejemplo, el gráfico de la Figura 6.6 (creado usando Microsoft Excel) traza la popularidad relativa de diferentes religiones en Estados Unidos. Hay al menos tres cosas mal en esta cifra:

• tiene gráficos superpuestos en cada una de las barras que no tienen nada que ver con los datos reales
• tiene una textura de fondo que distrae
• utiliza barras tridimensionales, que distorsionan los datos

Figura 6.6: Un ejemplo de chatarra gráfica.

6.2.4 Evitar distorsionar los datos

A menudo es posible usar la visualización para distorsionar el mensaje de un conjunto de datos. Una muy común es el uso de diferentes escalamientos de ejes para exagerar u ocultar un patrón de datos. Por ejemplo, digamos que nos interesa ver si los índices de delincuencia violenta han cambiado en EU. En la Figura 6.7, podemos ver estos datos trazados de formas que o bien hacen que parezca que el crimen se ha mantenido constante, o que se ha desplomado. ¡Los mismos datos pueden contar dos historias muy diferentes!

Figura 6.7: Datos de delitos de 1990 a 2014 trazados a lo largo del tiempo. Los paneles A y B muestran los mismos datos, pero con diferentes rangos de ejes. Datos obtenidos de https://www.ucrdatatool.gov/Search/Crime/State/RunCrimeStatebyState.cfm

Una de las principales controversias en la visualización estadística de datos es cómo elegir el eje Y, y en particular si siempre debe incluir cero. En su famoso libro “Cómo mentir con las estadísticas”, Darrell Huff argumentó fuertemente que siempre se debe incluir el punto cero en el eje Y. Por otra parte, Edward Tufte ha argumentado en contra de esto:

“En general, en una serie temporal, usa una línea base que muestre los datos no el punto cero; no gastes mucho espacio vertical vacío tratando de llegar hasta el punto cero a costa de ocultar lo que está pasando en la propia línea de datos”. (de https://qz.com/418083/its-ok-not-to-start-your-y-axis-at-zero/)

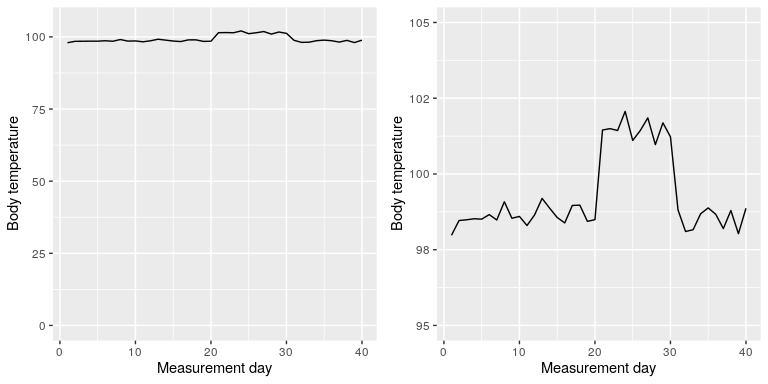
Ciertamente hay casos en los que usar el punto cero no tiene ningún sentido. Digamos que estamos interesados en trazar la temperatura corporal para un individuo a lo largo del tiempo. En la Figura 6.8 trazamos los mismos datos (simulados) con o sin cero en el eje Y. Debería ser obvio que al trazar estos datos con cero en el eje Y (Panel A) estamos desperdiciando mucho espacio en la figura, dado que la temperatura corporal de una persona viva ¡nunca podría llegar a cero! Al incluir cero, también estamos haciendo que el aparente salto de temperatura durante los días 21-30 sea mucho menos evidente. En general, mi inclinación por las gráficas de línea y las gráficas de dispersión es usar todo el espacio en la gráfica, a menos que sea realmente importante resaltar el punto cero.

Figura 6.8: Temperatura corporal a lo largo del tiempo, trazada con o sin el punto cero en el eje Y.

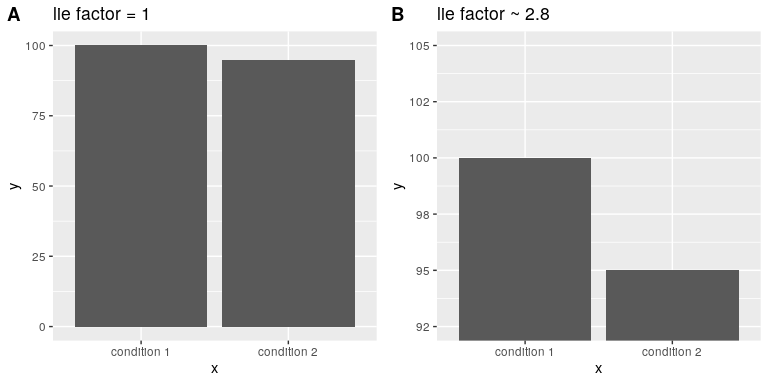
Edward Tufte introdujo el concepto del factor mentira para describir el grado en que las diferencias físicas en una visualización corresponden a la magnitud de las diferencias en los datos. Si un gráfico tiene un factor de mentira cerca de 1, entonces representa apropiadamente los datos, mientras que los factores de mentira lejos de uno reflejan una distorsión de los datos subyacentes.

El factor mentira apoya el argumento de que siempre se debe incluir el punto cero en un gráfico de barras en muchos casos. En la Figura 6.9 trazamos los mismos datos con y sin cero en el eje Y. En el panel A, la diferencia proporcional de área entre las dos barras es exactamente la misma que la diferencia proporcional entre los valores (es decir, factor de mentira = 1), mientras que en el Panel B (donde no se incluye cero) la diferencia proporcional en el área entre las dos barras es aproximadamente 2.8 veces mayor que la diferencia proporcional en los valores, y así exagera visualmente el tamaño de la diferencia.

Figura 6.9: Dos gráficos de barras con factores de mentira asociados.