8.10: Puntuaciones Z

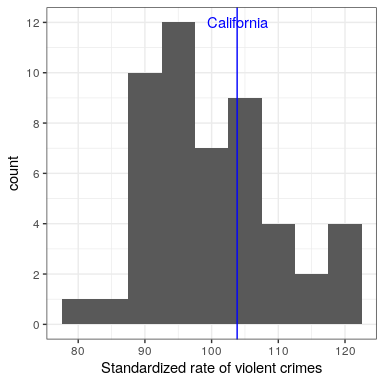
Habiendo caracterizado una distribución en términos de su tendencia central y variabilidad, a menudo es útil expresar las puntuaciones individuales en términos de dónde se sientan con respecto a la distribución general. Digamos que nos interesa caracterizar el nivel relativo de delitos en distintos estados, para determinar si California es un lugar particularmente peligroso. Podemos hacer esta pregunta usando datos para 2014 del sitio Uniforme de Reporte de Delitos del FBI. El panel izquierdo de la Figura 8.8 muestra un histograma del número de delitos violentos por estado, destacando el valor para California. Al mirar estos datos, parece que California es terriblemente peligrosa, con 153709 delitos en ese año.

Figura 8.8: Izquierda: Histograma del número de delitos violentos. El valor de CA se traza en azul. Derecha: Un mapa de los mismos datos, con número de delitos trazados para cada estado en color.

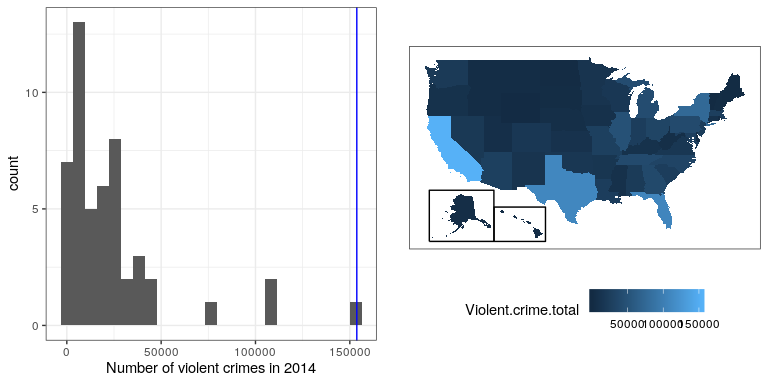
Con R también es fácil generar un mapa que muestre la distribución de una variable entre estados, que se presenta en el panel derecho de la Figura 8.8.

Se le puede haber ocurrido, sin embargo, que CA también tiene la mayor población de cualquier estado en EU, por lo que es razonable que también tenga un mayor número de delitos. Si trazamos los dos uno contra el otro (ver panel izquierdo de la Figura 8.9), vemos que existe una relación directa entre la población y el número de delitos.

Figura 8.9: Izquierda: Una trama de número de delitos versus población por estado. Derecha: Histograma de tasas de delincuencia per cápita, expresadas como delitos por cada 100 mil personas.

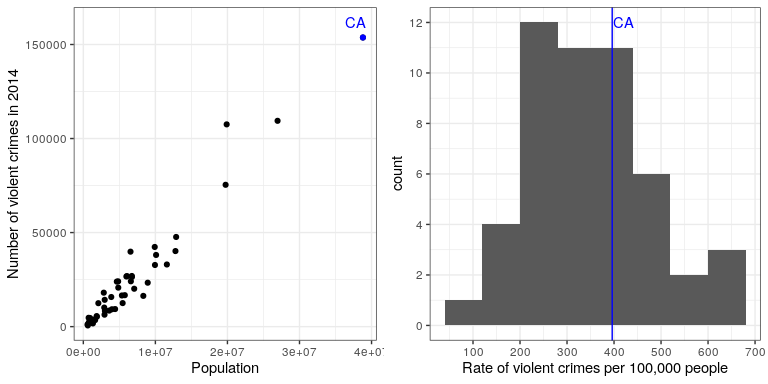
En lugar de usar los números brutos de delitos, deberíamos usar en su lugar la tasa de delitos violentos per cápita, que obtenemos dividiendo el número de delitos entre la población del estado. El conjunto de datos del FBI ya incluye este valor (expresado como tasa por cada 100 mil personas). Al observar el panel derecho de la Figura 8.9, vemos que California no es tan peligrosa después de todo — su tasa de criminalidad de 396.10 por cada 100 mil personas está un poco por encima de la media en todos los estados de 346.81, pero muy dentro del rango de muchos otros estados. Pero, ¿y si queremos tener una visión más clara de lo lejos que está del resto de la distribución?

La puntuación Z nos permite expresar datos de una manera que proporciona más información sobre la relación de cada punto de datos con la distribución general. La fórmula para calcular una puntuación Z para un punto de datos dado que conocemos el valor de la media poblacional$\ mu$y desviación estándar$\ sigma$es:

$$Z(x)=\frac{x-\mu }{\sigma }$$

Intuitivamente, puede pensar que una puntuación Z le indica qué tan lejos de la media se encuentra cualquier punto de datos, en unidades de desviación estándar. Podemos computar esto para los datos de la tasa delictiva, como se muestra en la Figura 8.10.

## [1] "mean of Z-scored data: 1.4658413372004e-16"

## [1] "std deviation of Z-scored data: 1"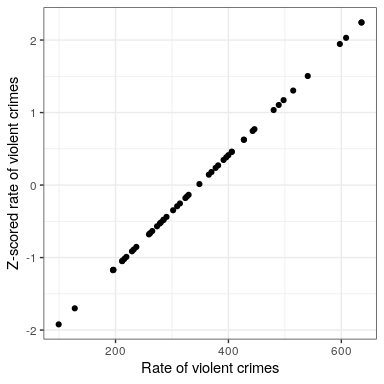

Figura 8.10: Gráfica de dispersión de los datos originales de la tasa delictiva contra los datos puntuados Z.

El diagrama de dispersión nos muestra que el proceso de puntuación Z no cambia la distribución relativa de los puntos de datos (visible en el hecho de que los datos originales y los datos con puntuación Z caen en línea recta cuando se trazan uno contra el otro), simplemente los desplaza para tener una media de cero y una desviación estándar de uno. Sin embargo, si miras de cerca, verás que la media no es exactamente cero, es simplemente muy pequeña. Lo que está pasando aquí es que la computadora representa números con cierta precisión numérica, lo que significa que hay números que no son exactamente cero, sino que son lo suficientemente pequeños como para que R los considere cero.

En la Figura 8.11 se muestran los datos de delitos con puntuación Z utilizando la vista geográfica.

Figura 8.11: Datos delictivos renderizados en un mapa de Estados Unidos, presentados como puntajes Z.

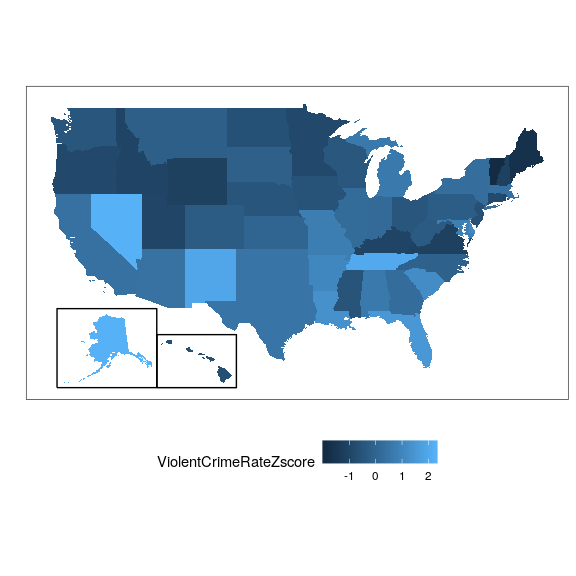
Esto nos proporciona una visión un poco más interpretable de los datos. Por ejemplo, podemos ver que Nevada, Tennessee y Nuevo México tienen tasas de criminalidad que son aproximadamente dos desviaciones estándar por encima de la media.

8.9.1 Interpretación de puntuaciones Z

La “Z” en “Z-score”” proviene del hecho de que la distribución normal estándar (es decir, una distribución normal con una media de cero y una desviación estándar de 1) a menudo se conoce como la distribución “Z”. Podemos usar la distribución normal estándar para ayudarnos a comprender qué puntuaciones Z específicas nos dicen sobre dónde se encuentra un punto de datos con respecto al resto de la distribución.

Figura 8.12: Densidad (arriba) y distribución acumulativa (abajo) de una distribución normal estándar, con cortes a una desviación estándar por encima o por debajo de la media.

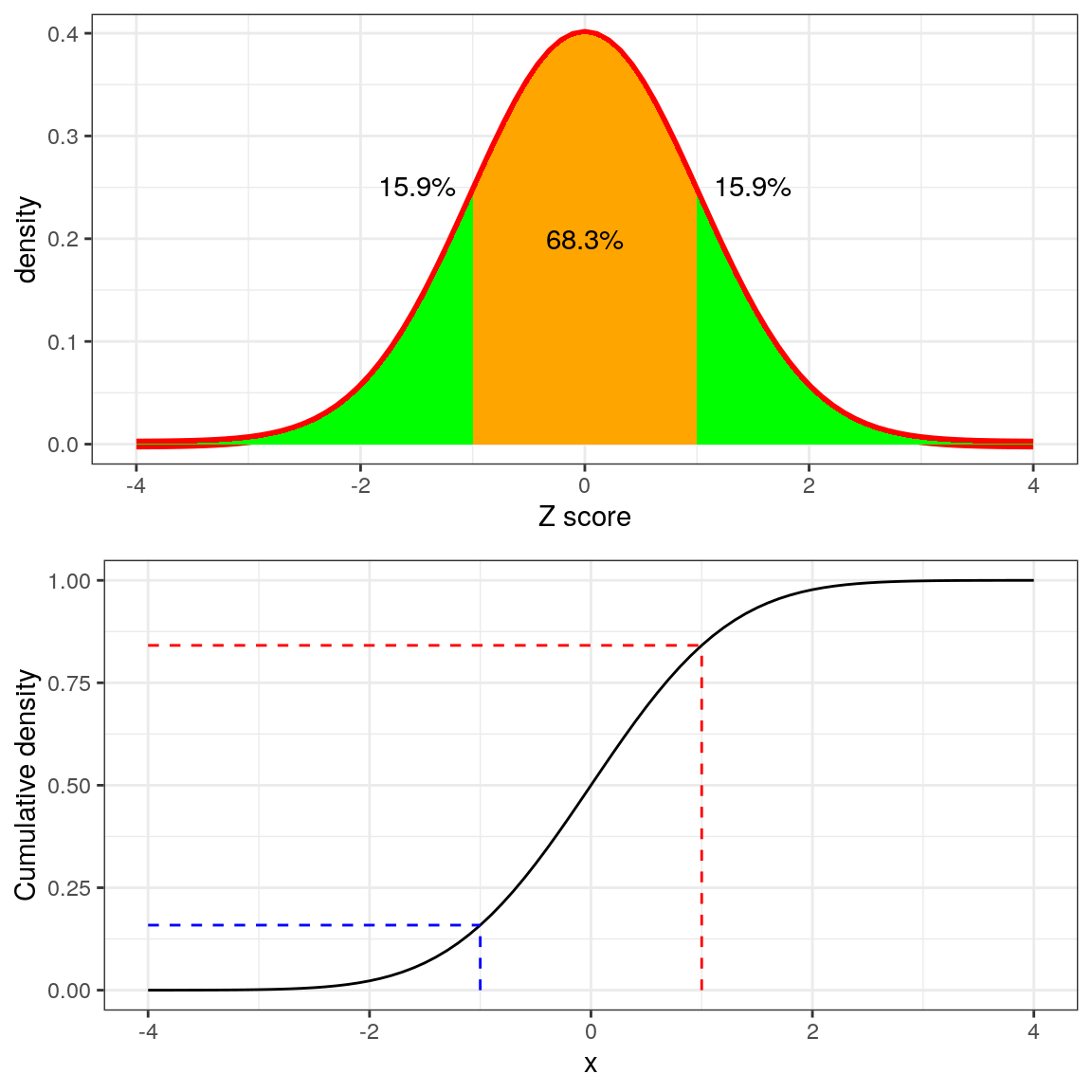
El panel superior en la Figura 8.12 muestra que esperamos que alrededor del 16% de los valores caigan en$Z\ ge 1$, y la misma proporción para caer en$Z\ le -1$.

Figura 8.13: Densidad (arriba) y distribución acumulativa (abajo) de una distribución normal estándar, con puntos de corte a dos desviaciones estándar por encima o por debajo de la media

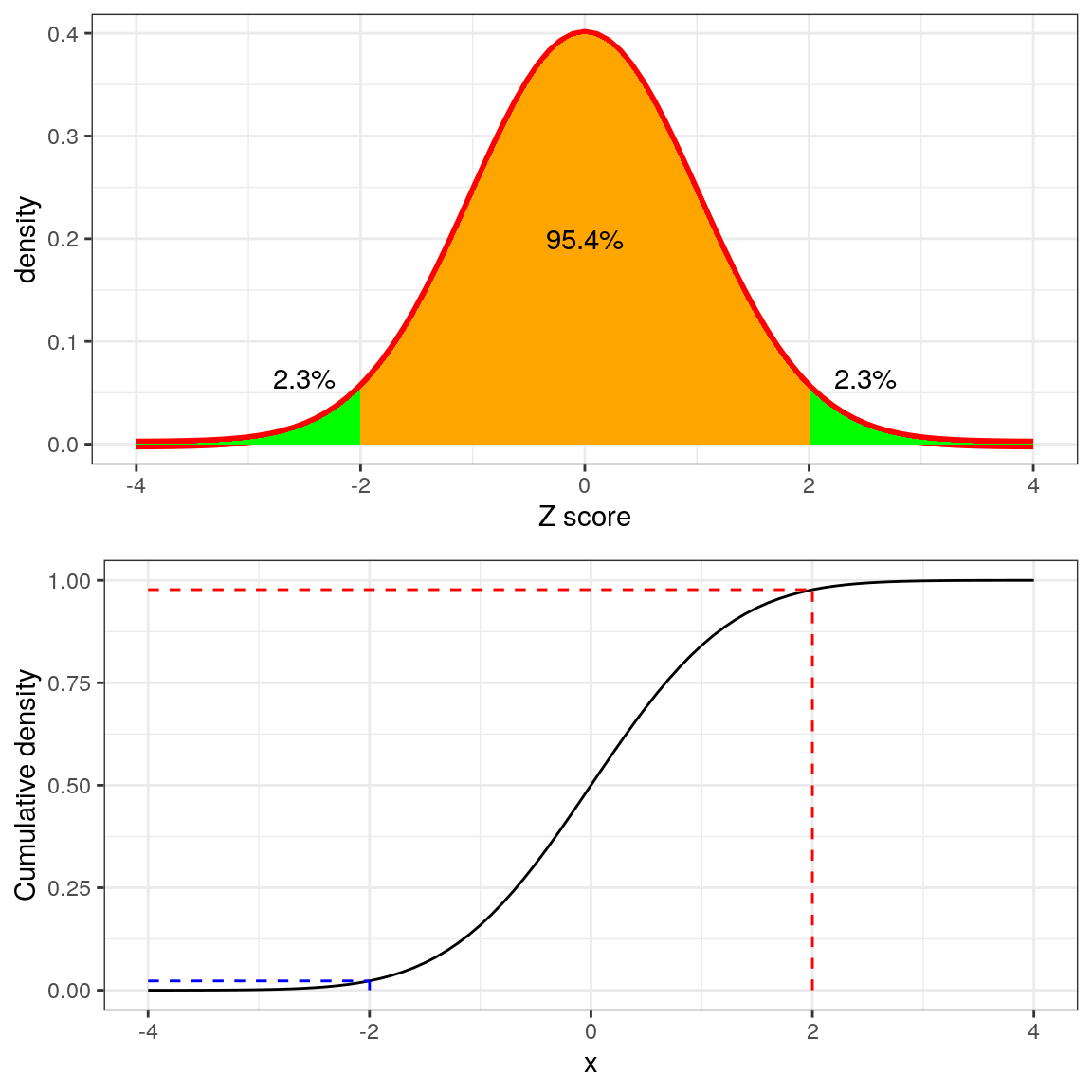
La Figura 8.13 muestra la misma gráfica para dos desviaciones estándar. Aquí vemos que solo alrededor del 2.3% de los valores caen en$Z\ le -2$y lo mismo en$Z\ ge 2$. Así, si conocemos la puntuación Z para un punto de datos en particular, podemos estimar qué tan probable o improbable sería encontrar un valor al menos tan extremo como ese valor, lo que nos permite poner los valores en un mejor contexto.

8.9.2 Puntuaciones estandarizadas

Digamos que en lugar de puntajes Z, queríamos generar puntajes estandarizados de delitos con una media de 100 y una desviación estándar de 10. Esto es similar a la estandarización que se realiza con puntajes de pruebas de inteligencia para generar el cociente de inteligencia (CI). Podemos hacer esto simplemente multiplicando las puntuaciones Z por 10 y luego sumando 100.

Figura 8.14: Datos delictivos presentados como puntajes estandarizados con media de 100 y desviación estándar de 10.

8.9.2.1 Uso de puntuaciones Z para comparar distribuciones

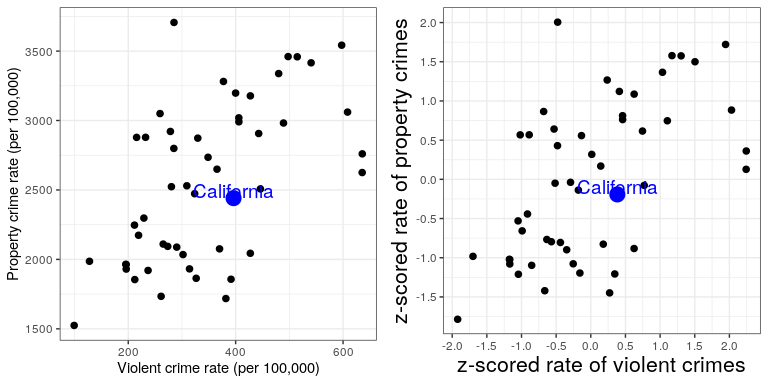
Una aplicación útil de las puntuaciones Z es comparar distribuciones de diferentes variables. Digamos que queremos comparar las distribuciones de delitos violentos y delitos patrimoniales en todos los estados. En el panel izquierdo de la Figura 8.15 trazamos los uno contra el otro, con CA trazada en azul. Como puede ver, las tasas brutas de delitos patrimoniales son mucho más altas que las tasas brutas de delitos violentos, por lo que no podemos simplemente comparar los números directamente. Sin embargo, podemos trazar las puntuaciones Z para estos datos entre sí (panel derecho de la Figura 8.15) — aquí nuevamente vemos que la distribución de los datos no cambia. Haber puesto los datos en puntuaciones Z para cada variable los hace comparables, y nos permite ver que California está en realidad justo en medio de la distribución en términos tanto de crimen violento como de delito contra la propiedad.

Figura 8.15: Gráfica de tasas de delitos violentos vs. patrimoniales (izquierda) y tasas de puntuación Z (derecha).

Agreguemos un factor más a la trama: Población. En el panel izquierdo de la Figura 8.16 mostramos esto usando el tamaño del símbolo de trazado, que a menudo es una forma útil de agregar información a una gráfica.

Figura 8.16: Izquierda: Gráfica de tasas de delitos violentos vs. patrimoniales, con tamaño poblacional presentado a través del tamaño del símbolo de trazado; California se presenta en azul. Derecha: Puntuaciones de diferencia por delitos violentos vs. patrimoniales, tramados contra población.

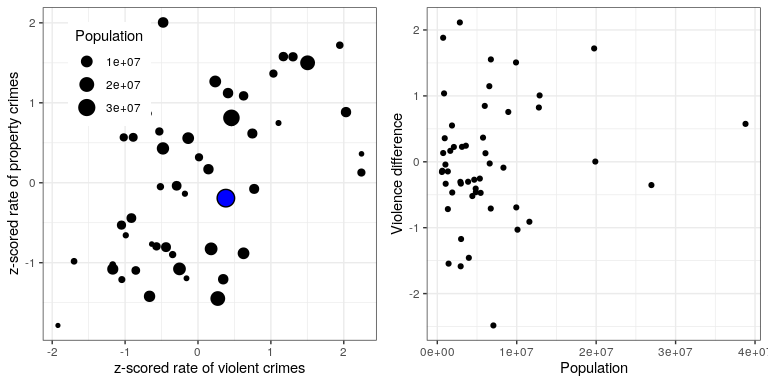
Debido a que los puntajes Z son directamente comparables, también podemos calcular una puntuación de “diferencia de violencia” que expresa la tasa relativa de delitos violentos a no violentos (propiedad) en todos los estados. Luego podemos trazar esos puntajes contra la población (ver panel derecho de la Figura 8.16). Esto muestra cómo podemos usar las puntuaciones Z para unir diferentes variables en una escala común.

Vale la pena señalar que los estados más pequeños parecen tener las mayores diferencias en ambos sentidos. Si bien puede ser tentador mirar cada estado e intentar determinar por qué tiene una puntuación de diferencia alta o baja, esto probablemente refleje el hecho de que las estimaciones obtenidas de muestras más pequeñas necesariamente van a ser más variables, como discutiremos en el capítulo posterior sobre Muestreo.