18.1: Intervalos de confianza
- Page ID
- 150488
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En lo que va del libro nos hemos centrado en estimar el valor específico de una estadística. Por ejemplo, digamos que queremos estimar el peso medio de los adultos en el conjunto de datos NHANES. Tomemos una muestra del conjunto de datos y calculemos la media. En esta muestra, el peso medio fue de 79.92 kilogramos. Nos referimos a esto como una estimación puntual ya que nos proporciona un solo número para describir la diferencia. Sin embargo, sabemos por nuestra anterior discusión sobre el error de muestreo que existe cierta incertidumbre sobre esta estimación, la cual es descrita por el error estándar. También debes recordar que el error estándar está determinado por dos componentes: la desviación estándar de la población (que es el numerador), y la raíz cuadrada del tamaño de la muestra (que está en el denominador). La desviación estándar poblacional es un parámetro desconocido pero fijo que no está bajo nuestro control, mientras que el tamaño de la muestra está bajo nuestro control. De esta manera, podemos disminuir nuestra incertidumbre sobre la estimación aumentando nuestro tamaño muestral —hasta el límite del tamaño total de la población, momento en el que no hay incertidumbre en absoluto porque podemos simplemente calcular el parámetro poblacional directamente a partir de los datos de toda la población.
También puede recordar que antes introdujimos el concepto de intervalo de confianza, que es una forma de describir nuestra incertidumbre sobre una estimación estadística. Recuerde que un intervalo de confianza describe un intervalo que contendrá en promedio el parámetro de población verdadera con una probabilidad dada; por ejemplo, el intervalo de confianza del 95% es un intervalo que capturará el parámetro de población verdadero 95% del tiempo. Observe nuevamente que esto no es una declaración sobre el parámetro population; cualquier intervalo de confianza en particular contiene o no el parámetro true. Como dijo Jerzy Neyman, el inventor del intervalo de confianza:
“El parámetro es una constante desconocida y no se puede hacer ninguna declaración de probabilidad con respecto a su valor”. (Neyman 1937)
El intervalo de confianza para la media se calcula como:
donde el valor crítico está determinado por la distribución muestral de la estimación. La pregunta importante, entonces, es cuál es esa distribución muestral.
18.1.1 Intervalos de confianza usando la distribución normal
Si conocemos la desviación estándar de la población, entonces podemos usar la distribución normal para calcular un intervalo de confianza. Normalmente no lo hacemos, pero para nuestro ejemplo del conjunto de datos NHANES lo hacemos (es 21.3 para el peso).
Digamos que queremos calcular un intervalo de confianza del 95% para la media. El valor crítico serían entonces los valores de la distribución normal estándar que capturan el 95% de la distribución; estos son simplemente el percentil 2.5 y el percentil 97.5 de la distribución, que podemos calcular usando la función qnorm () en R, y salir a. Así, el intervalo de confianza para la media () es:
Utilizando la media estimada de nuestra muestra (79.92) y la desviación estándar poblacional conocida, podemos calcular el intervalo de confianza de [77.28,82.56].
18.1.2 Intervalos de confianza usando la distribución t
Como se indicó anteriormente, si conociéramos la desviación estándar de la población, entonces podríamos usar la distribución normal para calcular nuestros intervalos de confianza. Sin embargo, en general no lo hacemos —en cuyo caso la distribución t es más apropiada como distribución muestral. Recuerde que la distribución t es ligeramente más amplia que la distribución normal, especialmente para muestras más pequeñas, lo que significa que los intervalos de confianza serán ligeramente más anchos de lo que harían si estuviéramos usando la distribución normal. Esto incorpora la incertidumbre extra que surge cuando hacemos conclusiones basadas en pequeñas muestras.
Podemos calcular el intervalo de confianza del 95% de manera similar al ejemplo de distribución normal anterior, pero el valor crítico está determinado por el percentil 2.5 y el percentil 97.5 de la distribución t, que podemos calcular usando la función qt () en R. Así, la confianza intervalo para la media () es:
dondees el valor t crítico. Para el ejemplo de peso NHANES (con tamaño de muestra de 250), el intervalo de confianza sería 79.92 +/- 1.97 [77.15 - 82.69].
Recuerda que esto no nos dice nada sobre la probabilidad de que el verdadero valor poblacional caiga dentro de este intervalo, ya que es un parámetro fijo (que sabemos que es 81.77 porque tenemos toda la población en este caso) y o bien cae o no dentro de este intervalo específico (en este caso, se hace). En cambio, nos dice que a la larga, si calculamos el intervalo de confianza usando este procedimiento, el 95% del tiempo que ese intervalo de confianza capturará el parámetro de población verdadero.
18.1.3 Intervalos de confianza y tamaño de muestra
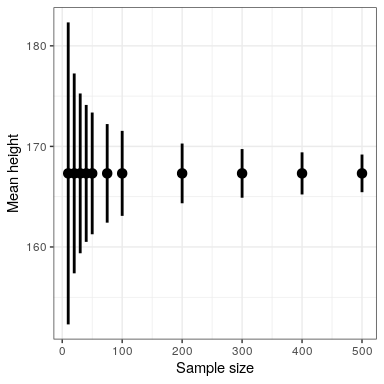
Debido a que el error estándar disminuye con el tamaño de la muestra, el intervalo de confianza media debería ser más estrecho a medida que aumenta el tamaño de la muestra, proporcionando límites progresivamente más estrechos en nuestra estimación. La Figura 18.1 muestra un ejemplo de cómo cambiaría el intervalo de confianza en función del tamaño de la muestra para el ejemplo de peso. De la figura es evidente que el intervalo de confianza se vuelve cada vez más estrecho a medida que aumenta el tamaño de la muestra, pero el aumento de las muestras proporciona rendimientos decrecientes, consistente con el hecho de que el denominador del término del intervalo de confianza es proporcional a la raíz cuadrada del tamaño de la muestra.
18.1.4 Cálculo de intervalos de confianza usando el bootstrap
En algunos casos no podemos asumir normalidad, o no conocemos la distribución muestral del estadístico. En estos casos, podemos usar el bootstrap (que introdujimos en el Capítulo 14). Como recordatorio, el bootstrap implica remuestrear repetidamente los datos con reemplazo, y luego usar la distribución del estadístico calculado en esas muestras como sustituto para la distribución de muestreo de la estadística. R incluye un paquete llamado boot que podemos usar para ejecutar el bootstrap y calcular intervalos de confianza. Siempre es bueno usar una función incorporada para calcular una estadística si está disponible, en lugar de codificarla desde cero, tanto porque te ahorra trabajo extra como porque la versión incorporada se probará mejor. Estos son los resultados cuando usamos boot () para calcular el intervalo de confianza para el peso en nuestra muestra NHANES:
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 1000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = bs, type = "perc")
##
## Intervals :
## Level Percentile
## 95% (77, 83 )
## Calculations and Intervals on Original ScaleEstos valores son bastante cercanos a los valores obtenidos usando la distribución t anterior, aunque no exactamente iguales.
18.1.5 Relación de intervalos de confianza con pruebas de hipótesis
Existe una estrecha relación entre los intervalos de confianza y las pruebas de hipótesis. En particular, si el intervalo de confianza no incluye la hipótesis nula, entonces la prueba estadística asociada sería estadísticamente significativa. Por ejemplo, si está probando si la media de una muestra es mayor que cero con, simplemente podría verificar para ver si el cero está contenido dentro del intervalo de confianza del 95% para la media.
Las cosas se ponen más complicadas si queremos comparar las medias de dos condiciones (Schenker y Gentleman 2001). Hay un par de situaciones que son claras. Primero, si cada media está contenida dentro del intervalo de confianza para la otra media, entonces ciertamente no hay diferencia significativa en el nivel de confianza elegido. Segundo, si no hay solapamiento entre los intervalos de confianza, entonces ciertamente hay una diferencia significativa en el nivel elegido; de hecho, esta prueba es sustancialmente conservadora, de tal manera que la tasa de error real será menor que el nivel elegido. Pero, ¿qué pasa con el caso en el que los intervalos de confianza se superponen entre sí pero no contienen los medios para el otro grupo? En este caso la respuesta depende de la variabilidad relativa de las dos variables, y no hay respuesta general. En general debemos evitar usar la “prueba visual” para intervalos de confianza superpuestos.


