20.1: Modelos Generativos

Última actualización
Guardar como PDF

Page ID: 150593

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Di que estás caminando por la calle y un amigo tuyo pasa por ahí pero no dice hola. Probablemente tratarías de decidir por qué sucedió esto — ¿No te vieron? ¿Están enojados contigo? ¿De repente estás enlucido con un escudo mágico de invisibilidad? Una de las ideas básicas detrás de las estadísticas bayesianas es que queremos inferir los detalles de cómo se están generando los datos, con base en los propios datos. En este caso, quieres usar los datos (es decir, el hecho de que tu amigo no saludó) para inferir el proceso que generó los datos (por ejemplo, si realmente te vieron o no, cómo se sienten por ti, etc.).

La idea detrás de un modelo generativo es que un proceso latente (invisible) genera los datos que observamos, generalmente con cierta cantidad de aleatoriedad en el proceso. Cuando tomamos una muestra de datos de una población y estimamos un parámetro a partir de la muestra, lo que estamos haciendo en esencia es tratar de aprender el valor de una variable latente (la media poblacional) que da lugar a través del muestreo a los datos observados (la media muestral). La Figura 20.1 muestra un esquema de esta idea.

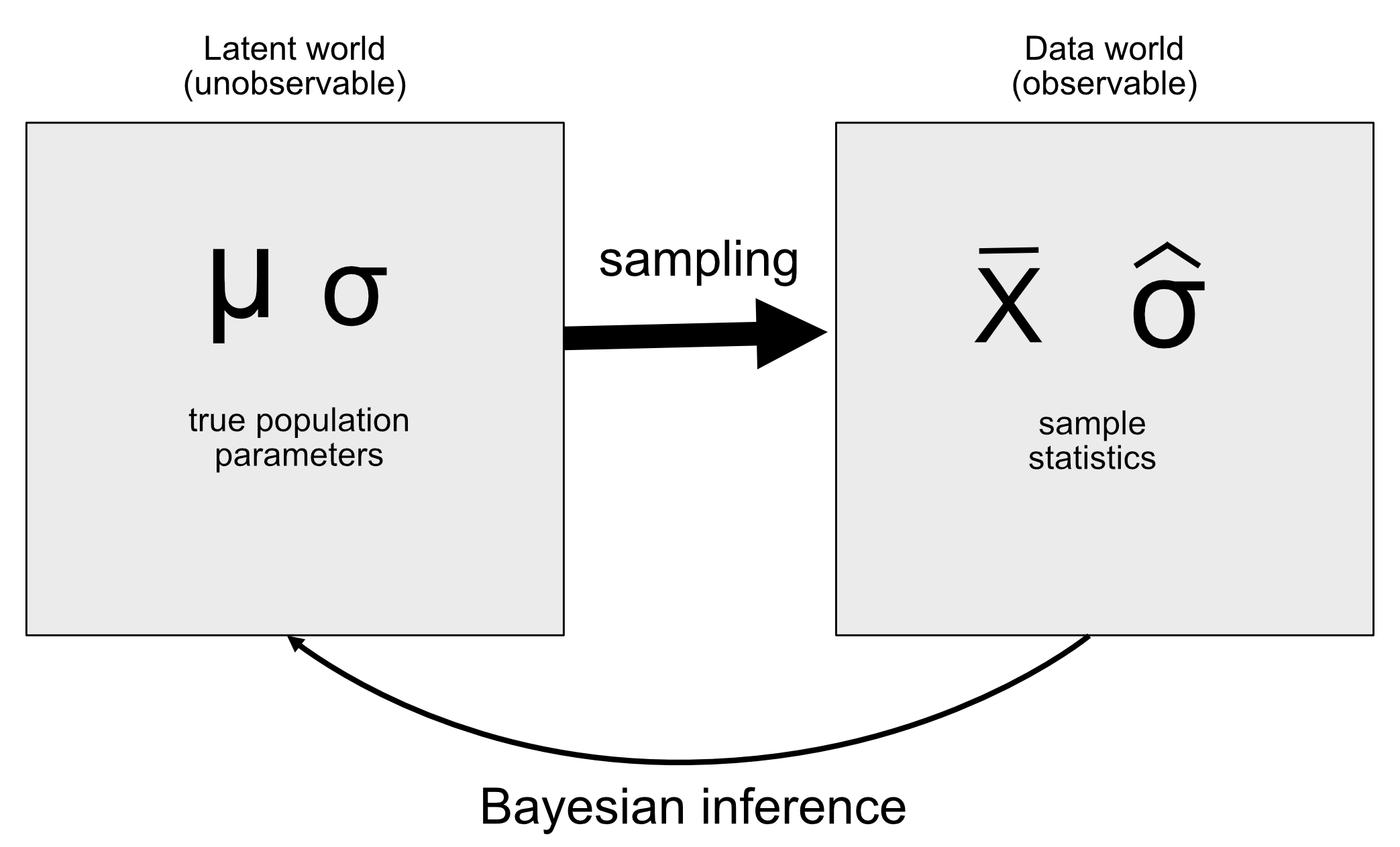
Figura 20.1: Un esquema de la idea de un modelo generativo.

Si conocemos el valor de la variable latente, entonces es fácil reconstruir cómo deberían ser los datos observados. Por ejemplo, digamos que estamos volteando una moneda que sabemos que es justa, tal que esperaríamos que aterrice en cabezas el 50% del tiempo. Podemos describir la moneda mediante una distribución binomial con un valor de $P_ {cabezas} =0.5$ , y luego podríamos generar muestras aleatorias a partir de tal distribución para ver cómo deberían ser los datos observados. No obstante, en general estamos en la situación opuesta: No conocemos el valor de la variable latente de interés, pero tenemos algunos datos que nos gustaría utilizar para estimarla.