24.6: Apéndice

Última actualización
Guardar como PDF

Page ID: 150528

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

24.6.1 Cuantificar la desigualdad: El índice de Gini

Antes de mirar el análisis reportado en la historia, primero es útil entender cómo se utiliza el índice de Gini para cuantificar la desigualdad. El índice de Gini suele definirse en términos de una curva que describe la relación entre el ingreso y la proporción de la población que tiene ingresos iguales o inferiores a ese nivel, conocida como curva de Lorenz. Sin embargo, otra forma de pensarlo es más intuitiva: Es la diferencia absoluta media relativa entre los ingresos, dividida por dos (de https://en.Wikipedia.org/wiki/Gini_coefficient):

$G =\ frac {\ displaystyle {\ suma_ {i=1} ^n\ suma_ {j=1} ^n\ izquierda| x_i - x_j\ derecha|}} {\ displaystyle {2n\ suma_ {i=1} ^n x_i}}$

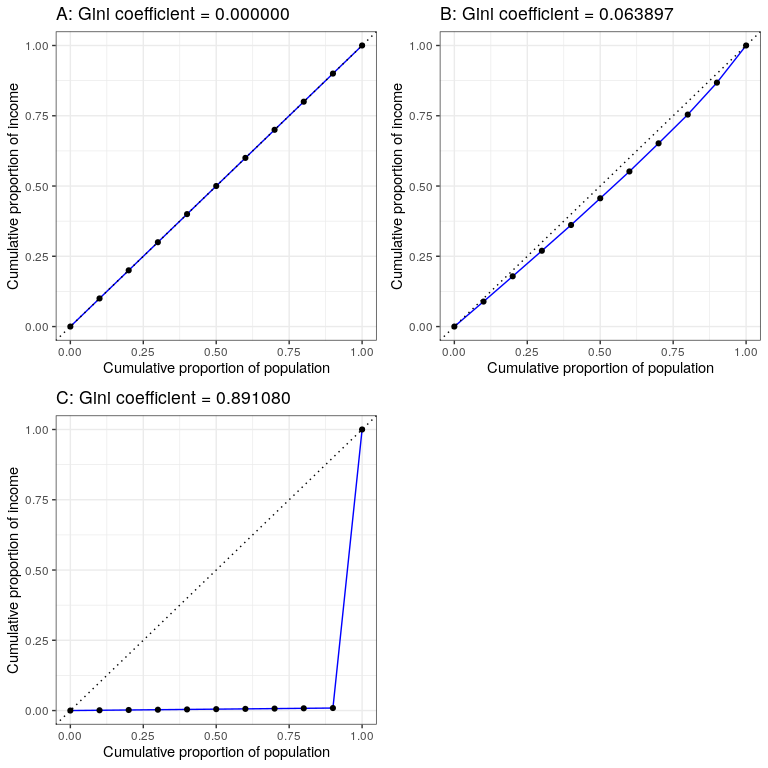
Lorenz curva para A) igualdad perfecta, B) ingreso normalmente distribuido, y C) alta desigualdad (ingresos iguales excepto para un individuo muy rico).

Figura 24.6: Curvas de Lorenz para A) igualdad perfecta, B) ingreso normalmente distribuido, y C) alta desigualdad (ingresos iguales excepto para un individuo muy rico).

La Figura 24.6 muestra las curvas de Lorenz para varias distribuciones de ingresos diferentes. El panel superior izquierdo (A) muestra un ejemplo con 10 personas donde todos tienen exactamente los mismos ingresos. La longitud de los intervalos entre puntos es igual, lo que indica que cada persona gana una parte idéntica del ingreso total en la población. El panel superior derecho (B) muestra un ejemplo donde los ingresos se distribuyen normalmente. El panel inferior izquierdo muestra un ejemplo con alta desigualdad; todos tienen ingresos iguales (40.000 dólares) a excepción de una persona, que tiene ingresos de 40 mil millones de dólares. Según el Censo de Estados Unidos, Estados Unidos tenía un índice de Gini de 0.469 en 2010, cayendo aproximadamente a mitad de camino entre nuestros ejemplos normalmente distribuidos y los ejemplos máximos inequiales.

24.6.2 Análisis de correlación bayesiana

También podemos analizar los datos de FiveThirtyEight utilizando el análisis bayesiano, lo que tiene dos ventajas. En primer lugar, nos proporciona una probabilidad posterior —en este caso, la probabilidad de que el valor de correlación supere cero. Segundo, la estimación bayesiana combina la evidencia observada con una previa, lo que tiene el efecto de regularizar la estimación de correlación, efectivamente tirándola hacia cero. Aquí podemos calcularlo usando la función jzs_cor del paquete BayesMed.

## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 50
##    Unobserved stochastic nodes: 4
##    Total graph size: 230
## 
## Initializing model

## $Correlation
## [1] 0.41
## 
## $BayesFactor
## [1] 11
## 
## $PosteriorProbability
## [1] 0.92

Obsérvese que la correlación estimada mediante el método bayesiano es ligeramente menor que la estimada utilizando el coeficiente de correlación estándar, lo que se debe a que la estimación se basa en una combinación de la evidencia y la previa, lo que efectivamente reduce la estimación hacia cero. No obstante, observe que el análisis bayesiano no es robusto al valor atípico, y aún así dice que hay evidencia bastante fuerte de que la correlación es mayor a cero.

Search

Text Color

Text Size

Margin Size

Font Type