26.6: ¿Qué significa realmente “predecir”?

Cuando hablamos de “predicción” en la vida cotidiana, generalmente nos estamos refiriendo a la capacidad de estimar el valor de alguna variable antes de ver los datos. Sin embargo, el término se suele utilizar en el contexto de regresión lineal para referirse al ajuste de un modelo a los datos; los valores estimados ($\hat{y}$

Como ejemplo, tomemos una muestra de 48 niños de NHANES y ajustemos un modelo de regresión para el peso que incluya varios regresores (edad, estatura, horas dedicadas a ver televisión y usar la computadora, e ingresos familiares) junto con sus interacciones.

Tabla 26.2: Raíz de error cuadrático medio para el modelo aplicado a datos originales y nuevos datos, y después de barajar el orden de la variable y (en esencia haciendo verdadera la hipótesis nula)

Tipo de datos	RMSE (datos originales)	RMSE (nuevos datos)
Datos verdaderos	3.0	21
Datos barajados	7.6	59

Aquí vemos que mientras que el modelo se ajusta a los datos originales mostró un ajuste muy bueno (solo apagado por unas pocas libras por individuo), el mismo modelo hace un trabajo mucho peor al predecir los valores de peso para los nuevos niños muestreados de la misma población (apagado por más de 25 libras por individuo). Esto sucede porque el modelo que especificamos es bastante complejo, ya que incluye no sólo cada una de las variables individuales, sino también todas las combinaciones posibles de ellas (es decir, sus interacciones), resultando en un modelo con 32 parámetros. Dado que se trata de casi tantos coeficientes como puntos de datos (es decir, las alturas de 48 hijos), el modelo sobreajusta los datos, al igual que la curva polinómica compleja en nuestro ejemplo inicial de sobreajuste en la Sección 8.4.

Otra forma de ver los efectos del sobreajuste es observar lo que sucede si barajamos aleatoriamente los valores de la variable de peso (que se muestra en la segunda fila de la tabla). Barajar aleatoriamente el valor debería hacer imposible predecir el peso a partir de las otras variables, porque no deben tener una relación sistemática. Esto nos muestra que incluso cuando no hay una relación verdadera que modelar (porque el barajado debería haber borrado la relación), el modelo complejo sigue mostrando un error muy bajo en sus predicciones, porque ajusta el ruido en el conjunto de datos específico. Sin embargo, cuando ese modelo se aplica a un nuevo conjunto de datos, vemos que el error es mucho mayor, como debería ser.

26.6.1 Validación cruzada

Un método que se ha desarrollado para ayudar a abordar el problema del sobreajuste se conoce como validación cruzada. Esta técnica es comúnmente utilizada dentro del campo del aprendizaje automático, que se enfoca en construir modelos que generalicen bien a nuevos datos, incluso cuando no tengamos un nuevo conjunto de datos para probar el modelo. La idea detrás de la validación cruzada es que ajustamos nuestro modelo repetidamente, cada vez dejando fuera un subconjunto de los datos, y luego probamos la capacidad del modelo para predecir los valores en cada subconjunto mantenido.

Figura 26.6: Esquema del procedimiento de validación cruzada.

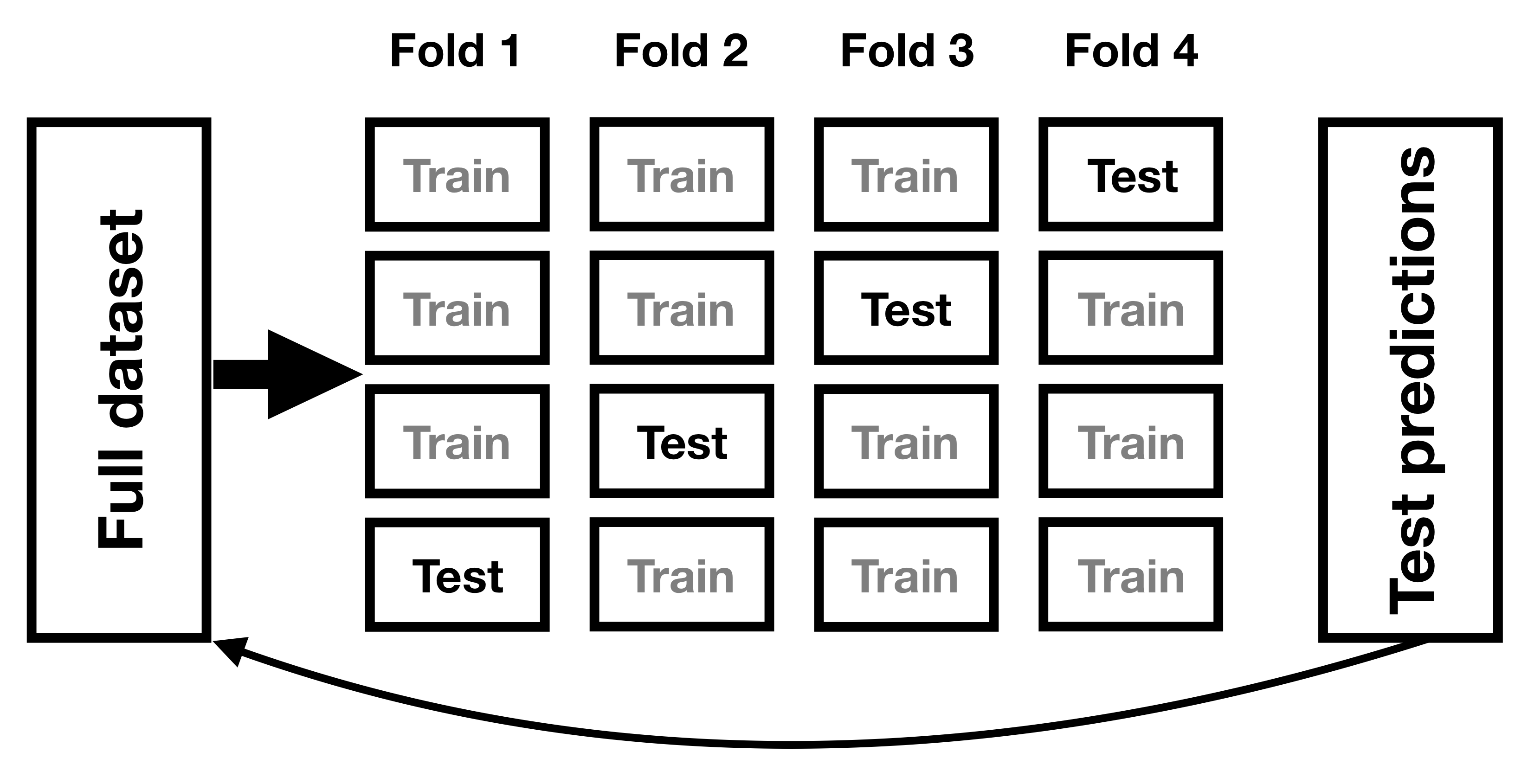
Veamos cómo funcionaría eso para nuestro ejemplo de predicción de peso. En este caso realizaremos una validación cruzada de 12 veces, lo que significa que dividiremos los datos en 12 subconjuntos, y luego ajustaremos el modelo 12 veces, en cada caso omitiendo uno de los subconjuntos y luego probando la capacidad del modelo para predecir con precisión el valor de la variable dependiente para esos puntos de datos suspendidos . El paquete caret en R nos proporciona la capacidad de ejecutar fácilmente la validación cruzada en nuestro conjunto de datos. Usando esta función podemos ejecutar la validación cruzada en 100 muestras del conjunto de datos NHANES, y calcular el RMSE para la validación cruzada, junto con el RMSE para los datos originales y un nuevo conjunto de datos, como calculamos anteriormente.

Cuadro 26.3: Raíz de error cuadrático medio a partir de validación cruzada y nuevos datos, mostrando que la validación cruzada proporciona una estimación razonable del desempeño del modelo en nuevos datos.

	Error cuadrático medio raíz
Datos originales	3
Nuevos datos	24
Validación cruzada	146

Aquí vemos que la validación cruzada nos da una estimación de precisión predictiva que está mucho más cerca de lo que vemos con un conjunto de datos completamente nuevo que a la precisión inflada que vemos con el conjunto de datos original; de hecho, es incluso un poco más pesimista que el promedio de un nuevo conjunto de datos, probablemente porque sólo se está utilizando una parte de los datos para entrenar a cada uno de los modelos.

Tenga en cuenta que usar correctamente la validación cruzada es complicado, y se recomienda que consulte con un experto antes de usarla en la práctica. Sin embargo, esta sección ojalá te haya mostrado tres cosas:

• “Predicción” no siempre significa lo que piensas que significa
• Los modelos complejos pueden sobreajustar los datos muy mal, de tal manera que uno puede ver una predicción aparentemente buena incluso cuando no hay una señal verdadera que predecir
• Debe ver las afirmaciones sobre la precisión de la predicción de manera muy escéptica a menos que se hayan hecho usando los métodos apropiados.