26.5: Criticar nuestro modelo y verificar suposiciones

Última actualización
Guardar como PDF

Page ID: 150880

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

El dicho “basura dentro, basura afuera” es tan cierto para las estadísticas como en cualquier otro lugar. En el caso de los modelos estadísticos, tenemos que asegurarnos de que nuestro modelo esté debidamente especificado y que nuestros datos sean apropiados para el modelo.

Cuando decimos que el modelo está “debidamente especificado”, queremos decir que hemos incluido el conjunto apropiado de variables independientes en el modelo. Ya hemos visto ejemplos de modelos mal especificados, en la Figura 8.3. Recuerde que vimos varios casos en los que el modelo no logró dar cuenta adecuadamente de los datos, como no incluir una intercepción. Al construir un modelo, debemos asegurarnos de que incluya todas las variables apropiadas.

También tenemos que preocuparnos por si nuestro modelo sacifica los supuestos de nuestros métodos estáticos. Una de las suposiciones más importantes que hacemos al usar el modelo lineal general es que los residuos (es decir, la diferencia entre las predicciones del modelo y los datos reales) se distribuyen normalmente. Esto puede fallar por muchas razones, ya sea porque el modelo no se especificó correctamente o porque los datos que estamos modelando son inapropiados.

Podemos usar algo llamado una gráfica Q-Q (cuantil-cuantil) para ver si nuestros residuos están distribuidos normalmente. Ya has encontrado cuantiles — son el valor que corta una proporción particular de una distribución acumulativa.La gráfica Q-Q presenta los cuantiles de dos distribuciones una contra la otra; en este caso, presentaremos los cuantiles de los datos reales de los cuantiles de una normal distribución. La Figura 26.5 muestra ejemplos de dos gráficas Q-Q de este tipo. El panel izquierdo muestra una gráfica Q-Q para datos de una distribución normal, mientras que el panel derecho muestra una gráfica Q-Q a partir de datos no normales. Los puntos de datos en el panel derecho divergen sustancialmente de la línea, reflejando el hecho de que normalmente no están distribuidos.

qq_df <- tibble(norm=rnorm(100),
                unif=runif(100))

p1 <- ggplot(qq_df,aes(sample=norm)) + 
  geom_qq() + 
  geom_qq_line() + 
  ggtitle('Normal data')

p2 <- ggplot(qq_df,aes(sample=unif)) + 
  geom_qq() + 
  geom_qq_line()+ 
  ggtitle('Non-normal data')

plot_grid(p1,p2)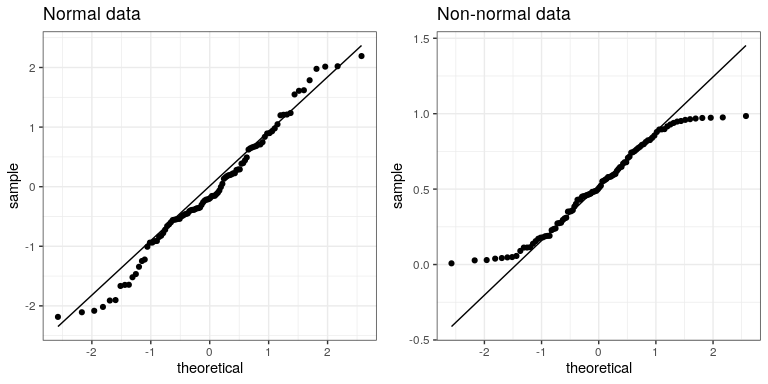

Figura 26.5: Gráficas Q-Q de datos normales (izquierda) y no normales (derecha). La línea muestra el punto en el que los ejes x e y son iguales.

Los diagnósticos del modelo se explorarán con más detalle en el siguiente capítulo.