26.8: Apéndice
- Page ID
- 150860
26.8.1 Estimación de parámetros de regresión lineal
Generalmente estimamos los parámetros de un modelo lineal a partir de datos utilizando álgebra lineal, que es la forma de álgebra que se aplica a vectores y matrices. Si no estás familiarizado con el álgebra lineal, no te preocupes, en realidad no necesitarás usarlo aquí, ya que R hará todo el trabajo por nosotros. Sin embargo, una breve excursión en álgebra lineal puede proporcionar una idea de cómo se estiman los parámetros del modelo en la práctica.
Primero, presentemos la idea de vectores y matrices; ya los has encontrado en el contexto de R, pero los revisaremos aquí. Una matriz es un conjunto de números que están dispuestos en un cuadrado o rectángulo, de tal manera que hay una o más dimensiones a través de las cuales varía la matriz. Es costumbre colocar diferentes unidades de observación (como personas) en las filas, y diferentes variables en las columnas. Tomemos nuestros datos de tiempo de estudio desde arriba. Podríamos organizar estos números en una matriz, que tendría ocho filas (una por cada alumno) y dos columnas (una para el tiempo de estudio y otra para el grado). Si estás pensando “eso suena como un marco de datos en R” ¡tienes toda la razón! De hecho, un marco de datos es una versión especializada de una matriz, y podemos convertir un marco de datos en una matriz usando la función.matrix ().
df <-
tibble(
studyTime = c(2, 3, 5, 6, 6, 8, 10, 12) / 3,
priorClass = c(0, 1, 1, 0, 1, 0, 1, 0)
) %>%
mutate(
grade =
studyTime * betas[1] +
priorClass * betas[2] +
round(rnorm(8, mean = 70, sd = 5))
)
df_matrix <-
df %>%
dplyr::select(studyTime, grade) %>%
as.matrix()Podemos escribir el modelo lineal general en álgebra lineal de la siguiente manera:
Esto se parece mucho a la ecuación anterior que usamos, excepto que las letras están todas en mayúscula, lo que está destinado a expresar el hecho de que son vectores.
Sabemos que los datos de grado entran en la matriz Y, pero lo que entra en el
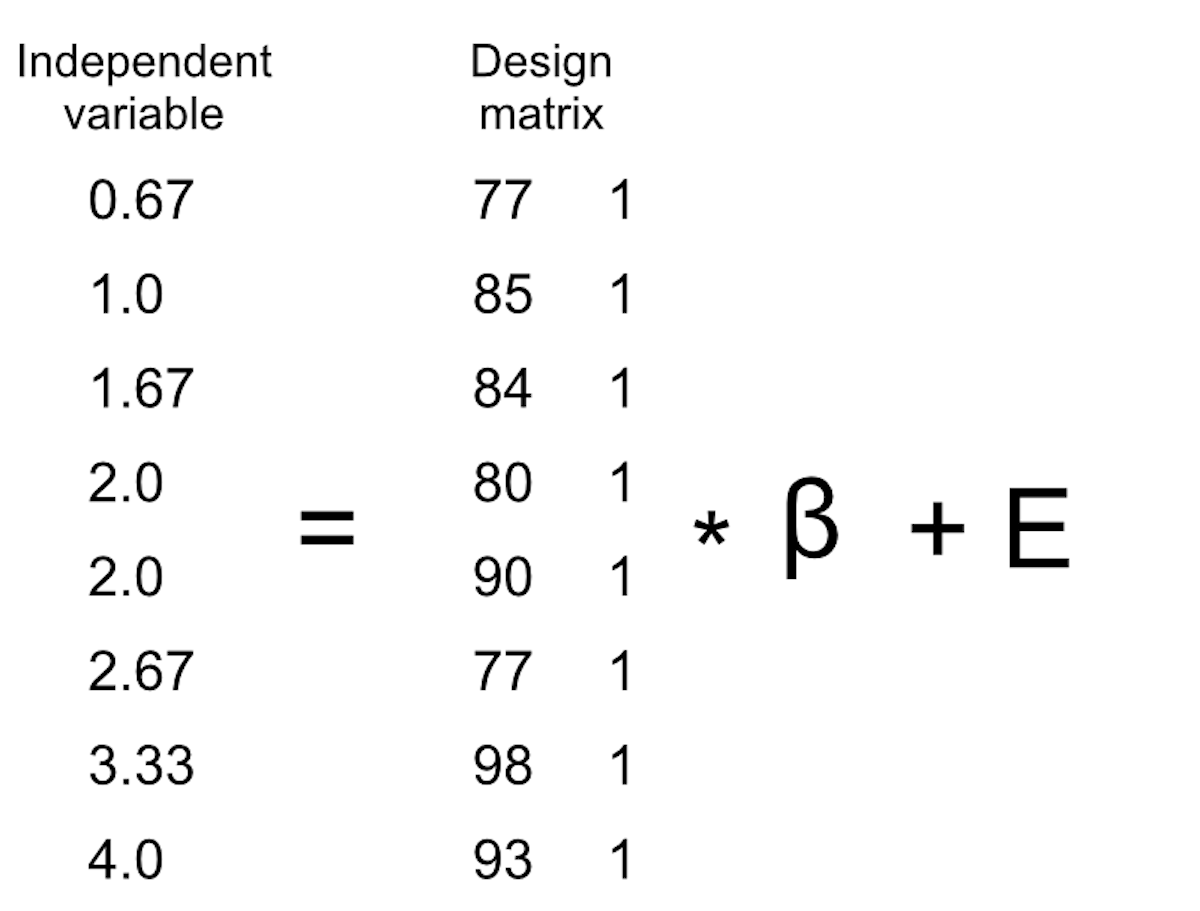
Las reglas de multiplicación matricial nos dicen que las dimensiones de las matrices tienen que coincidir entre sí; en este caso, la matriz de diseño tiene dimensiones de 8 (filas) X 2 (columnas) y la variable Y tiene dimensiones de 8 X 1. Por lo tanto, ella matriz necesita tener dimensiones 2 X 1, ya que una matriz de 8 X 2 multiplicada por una matriz de 2 X 1 da como resultado una matriz de 8 X 1 (ya que las dimensiones medias coincidentes caen). La interpretación de los dos valores en elmatriz es que son los valores a multiplicar por tiempo de estudio y 1 respectivamente para obtener la calificación estimada para cada individuo. También podemos ver el modelo lineal como un conjunto de ecuaciones individuales para cada individuo:
...
Recuerde que nuestro objetivo es determinar los mejores valores de ajuste dedados los valores conocidos dey. Una forma ingenua de hacer esto sería resolver parausando álgebra simple — aquí dejamos caer el término de errorporque está fuera de nuestro control:
El reto aquí es queyson ahora matrices, no números únicos — sino que las reglas del álgebra lineal nos dicen cómo dividir por una matriz, que es lo mismo que multiplicar por la inversa de la matriz (referida como). Podemos hacer esto en R:
# compute beta estimates using linear algebra
#create Y variable 8 x 1 matrix
Y <- as.matrix(df$grade)
#create X variable 8 x 2 matrix
X <- matrix(0, nrow = 8, ncol = 2)
#assign studyTime values to first column in X matrix
X[, 1] <- as.matrix(df$studyTime)
#assign constant of 1 to second column in X matrix
X[, 2] <- 1
# compute inverse of X using ginv()
# %*% is the R matrix multiplication operator
beta_hat <- ginv(X) %*% Y #multiple the inverse of X by Y
print(beta_hat)## [,1]
## [1,] 4.3
## [2,] 76.0Todo aquel que esté interesado en el uso serio de los métodos estadísticos está muy animado a invertir algo de tiempo en el aprendizaje del álgebra lineal, ya que proporciona la base para casi todas las herramientas que se utilizan en la estadística estándar.


