30.1: El Proceso de Modelado Estadístico

Hay un conjunto de pasos por los que generalmente pasamos cuando queremos usar nuestro modelo estadístico para probar una hipótesis científica:

1. Especifique su pregunta de interés
2. Identificar o recopilar los datos apropiados
3. Preparar los datos para su análisis
4. Determinar el modelo apropiado
5. Ajusta el modelo a los datos
6. Criticar el modelo para asegurarse de que se ajusta correctamente
7. Probar hipótesis y cuantificar el tamaño del efecto

Veamos un ejemplo real. En 2007, Christopher Gardner y colegas de Stanford publicaron un estudio en el Journal of the American Medical Association titulado “Comparación de las dietas Atkins, Zone, Ornish y APREND para el cambio de peso y factores de riesgo relacionados entre las mujeres premenopáusicas con sobrepeso La pérdida de peso de la A a la Z Estudio: Un ensayo aleatorizado” (Gardner et al. 2007).

30.1.1 1: Especifique su pregunta de interés

Según los autores, el objetivo de su estudio fue:

Comparar 4 dietas para bajar de peso que representan un espectro de ingesta baja a alta de carbohidratos para efectos sobre la pérdida de peso y variables metabólicas relacionadas.

30.1.2 2: Identificar o recoger los datos apropiados

Para responder a su pregunta, los investigadores asignaron aleatoriamente a cada una de 311 mujeres con sobrepeso/obesidad a una de cuatro dietas diferentes (Atkins, Zona, Ornish o APREND), y midieron su peso y otras medidas de salud a lo largo del tiempo.

Los autores registraron un gran número de variables, pero para la cuestión principal de interés centrémonos en una sola variable: el Índice de Masa Corporal (IMC). Además, dado que nuestro objetivo es medir los cambios duraderos en el IMC, solo veremos la medición tomada a los 12 meses después del inicio de la dieta.

30.1.3 3: Preparar los datos para su análisis

Figura 30.1: Gráficas de violín para cada condición, con el percentil 50 (es decir, la mediana) mostrado como una línea negra para cada grupo.

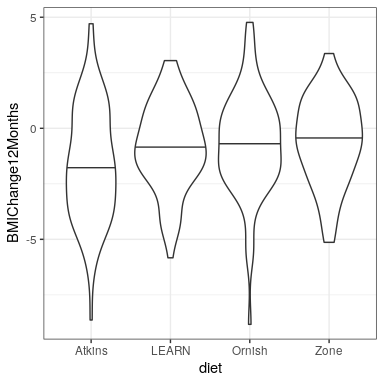
Los datos reales del estudio de la A a la Z no están disponibles públicamente, por lo que utilizaremos los datos resumidos reportados en su trabajo para generar algunos datos sintéticos que coincidan aproximadamente con los datos obtenidos en su estudio. Una vez que tengamos los datos, podemos visualizarlos para asegurarnos de que no haya valores atípicos. Las parcelas de violín son útiles para ver la forma de las distribuciones, como se muestra en la Figura 30.1. Esos datos parecen bastante razonables -en particular, no parece haber valores atípicos serios. Sin embargo, podemos ver que las distribuciones parecen diferir un poco en su varianza, con Atkins y Ornish mostrando mayor variabilidad que las otras.

Esto significa que cualquier análisis que asuma que las varianzas son iguales entre grupos podría ser inapropiado. Afortunadamente, el modelo ANOVA que planeamos usar es bastante robusto para esto.

30.1.4 4. Determinar el modelo apropiado

Hay varias preguntas que debemos hacer para determinar el modelo estadístico apropiado para nuestro análisis.

• ¿Qué tipo de variable dependiente?
  • IMC: continuo, aproximadamente distribuido normalmente
• ¿Qué estamos comparando?
  • IMC medio en cuatro grupos de dieta
  • ANOVA es apropiado
• ¿Son independientes las observaciones?
  • La asignación aleatoria y el uso de puntuaciones de diferencia deben garantizar que la asunción de independencia sea apropiada

30.1.5 5. Ajusta el modelo a los datos

Vamos a ejecutar un ANOVA sobre el cambio de IMC para compararlo entre las cuatro dietas. Resulta que en realidad no necesitamos generar las variables codificadas tontas nosotros mismos; si pasamos lm () una variable categórica, automáticamente las generará para nosotros.

## 
## Call:
## lm(formula = BMIChange12Months ~ diet, data = dietDf)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -8.14  -1.37   0.07   1.50   6.33 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -1.622      0.251   -6.47  3.8e-10 ***
## dietLEARN      0.772      0.352    2.19   0.0292 *  
## dietOrnish     0.932      0.356    2.62   0.0092 ** 
## dietZone       1.050      0.352    2.98   0.0031 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.2 on 307 degrees of freedom
## Multiple R-squared:  0.0338, Adjusted R-squared:  0.0243 
## F-statistic: 3.58 on 3 and 307 DF,  p-value: 0.0143

Tenga en cuenta que lm generó automáticamente variables ficticias que corresponden a tres de las cuatro dietas, dejando la dieta Atkins sin una variable ficticia. Esto significa que el intercepto modela la dieta Atkins, y las otras tres variables modelan la diferencia entre cada una de esas dietas y la dieta Atkins. Por defecto, lm () trata el primer valor (en orden alfabético) como línea base.

30.1.6 6. Criticar el modelo para asegurarse de que se ajusta correctamente

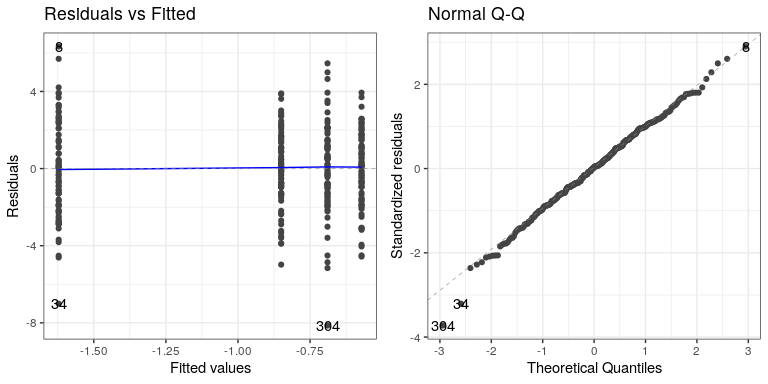
Lo primero que queremos hacer es criticar el modelo para asegurarnos de que sea apropiado. Una cosa que podemos hacer es mirar los residuos del modelo. En el panel izquierdo de Figura?? , trazamos los residuos para cada individuo agrupados por dieta, los cuales se posicionan por la media para cada dieta. No hay diferencias obvias en los residuos entre las condiciones, aunque hay un par de puntos de datos (#34 y #304) que parecen ser ligeros valores atípicos.

Otra suposición importante de las pruebas estadísticas que aplicamos a los modelos lineales es que los residuos del modelo se distribuyen normalmente. El panel derecho de Figura?? muestra una gráfica Q-Q (cuantil-cuantil), que grafica los residuos contra sus valores esperados en función de sus cuantiles en la distribución normal. Si los residuos se distribuyen normalmente entonces los puntos de datos deberían caer a lo largo de la línea discontinua — en este caso se ve bastante bien, excepto por esos dos valores atípicos que una vez más son evidentes aquí.

30.1.7 7. Probar hipótesis y cuantificar el tamaño del efecto

Primero echemos un vistazo al resumen de los resultados del ANOVA, que se muestra en el Paso 5 anterior. La prueba F significativa nos muestra que existe una diferencia significativa entre las dietas, pero también debemos tener en cuenta que el modelo en realidad no da cuenta de mucha varianza en los datos; el valor de R cuadrado es de solo 0.03, lo que demuestra que el modelo solo representa un pequeño porcentaje de la varianza en la pérdida de peso. Así, no quisiéramos sobreinterpretar este resultado.

El resultado significativo tampoco nos dice qué dietas difieren de cuáles otras. Podemos obtener más información comparando medias entre condiciones usando la función emmeans () (“medias marginales estimadas”):

##  diet   emmean    SE  df lower.CL upper.CL .group
##  Atkins  -1.62 0.251 307    -2.11    -1.13  a    
##  LEARN   -0.85 0.247 307    -1.34    -0.36  ab   
##  Ornish  -0.69 0.252 307    -1.19    -0.19   b   
##  Zone    -0.57 0.247 307    -1.06    -0.08   b   
## 
## Confidence level used: 0.95 
## P value adjustment: tukey method for comparing a family of 4 estimates 
## significance level used: alpha = 0.05

Las letras en la columna más a la derecha nos muestran cuáles de los grupos difieren entre sí, utilizando un método que se ajusta para el número de comparaciones que se están realizando. Esto demuestra que las dietas Atkins y LEARND no difieren entre sí (ya que comparten la letra a), y las dietas Learn, Ornish y Zone no difieren entre sí (ya que comparten la letra b), pero la dieta Atkins difiere de las dietas Ornish y Zone (ya que no comparten letras).

30.1.7.1 Factor Bayes

Digamos que queremos tener una mejor manera de describir la cantidad de pruebas aportadas por los datos. Una forma de hacerlo es computar un factor Bayes, lo que podemos hacer ajustando el modelo completo (incluida la dieta) y el modelo reducido (sin dieta) y luego comparando su ajuste. Para el modelo reducido, solo incluimos un 1, que le dice al programa de ajuste que solo se ajuste a una intercepción. Tenga en cuenta que esto tardará unos minutos en ejecutarse.

Esto nos muestra que existe evidencia muy fuerte (factor Bayes de casi 100) de diferencias entre las dietas.

30.1.8 ¿Qué pasa con los posibles confundimientos?

Si observamos más de cerca el artículo de Garder, veremos que también reportan estadísticas sobre cuántos individuos de cada grupo habían sido diagnosticados con síndrome metabólico, que es un síndrome caracterizado por hipertensión arterial, glucosa alta en la sangre, exceso de grasa corporal alrededor de la cintura y anormal niveles de colesterol y se asocia con un mayor riesgo de problemas cardiovasculares. Primero agreguemos esos datos en el marco de datos de resumen:

Cuadro 30.1: Presencia de síndrome metabólico en cada grupo en el estudio AtoZ.

Dieta	N	P (síndrome metabólico)
Atkins	77	0.29
APRENDER	79	0.25
Ornish	76	0.38
Zona	79	0.34

Al observar los datos parece que las tasas son ligeramente diferentes entre los grupos, con más casos de síndrome metabólico en las dietas Ornish y Zone —que fueron exactamente las dietas con peores resultados. Digamos que nos interesa probar si la tasa del síndrome metabólico fue significativamente diferente entre los grupos, ya que esto podría preocuparnos de que estas diferencias pudieran haber afectado los resultados de los resultados de la dieta.

30.1.8.1 Determinar el modelo apropiado

• ¿Qué tipo de variable dependiente?
  • proporciones
• ¿Qué estamos comparando?
  • proporción con síndrome metabólico en cuatro grupos de dieta
  • La prueba de chi-cuadrado para la bondad de ajuste es apropiada contra hipótesis nula de ninguna diferencia

Calculemos esa estadística usando la función chisq.test (). Aquí usaremos la opción simulate.p.value, que ayudará a lidiar con el relativamente pequeño

## 
##  Pearson's Chi-squared test
## 
## data:  contTable
## X-squared = 4, df = 3, p-value = 0.3

Esta prueba muestra que no existe una diferencia significativa entre medias. Sin embargo, no nos dice cuán seguros estamos de que no hay diferencia; recuerda que bajo NHST, siempre estamos trabajando bajo el supuesto de que el nulo es verdadero a menos que los datos nos muestren suficiente evidencia para hacernos rechazar esta hipótesis nula.

¿Y si queremos cuantificar las pruebas a favor o en contra del nulo? Podemos hacer esto usando el factor Bayes.

## Bayes factor analysis
## --------------
## [1] Non-indep. (a=1) : 0.058 ±0%
## 
## Against denominator:
##   Null, independence, a = 1 
## ---
## Bayes factor type: BFcontingencyTable, independent multinomial

Esto nos muestra que la hipótesis alternativa es 0.058 veces más probable que la hipótesis nula, lo que significa que la hipótesis nula es 1/0.058 ~ 17 veces más probable que la hipótesis alternativa dada estos datos. Esto es bastante fuerte, si no completamente abrumador, evidencia.