1.1: Introducción y ejemplos
- Page ID
- 148673
La primera definición aclara la noción de análisis de series temporales.
Definición 1.1.1: Series de Tiempo
\(T \neq \emptyset\)Sea un conjunto de índices, convenientemente pensándose como “tiempo”. Una familia\((X_t\colon t\in T)\) de variables aleatorias (funciones aleatorias) se denomina proceso estocástico. Una realización de\((X_t\colon t\in T)\) se llama serie temporal. Utilizaremos la notación\((x_t\colon t\in T)\) en el discurso.
Las opciones más comunes para el conjunto de índices T incluyen los enteros\(\mathbb{Z}=\{0,\pm 1,\pm 2,\ldots\}\), los enteros positivos\(\mathbb{N}=\{1,2,\ldots\}\), los enteros no negativos\(\mathbb{N}_0=\{0,1,2,\ldots\}\), los números reales\(\mathbb{R}=(-\infty,\infty)\) y la hallínea positiva\(\mathbb{R}_+=[0,\infty)\). Esta clase se ocupa principalmente de los tres primeros casos que se subsumen bajo la noción de análisis de series de tiempo discretas.
A menudo el proceso estocástico\((X_t\colon t\in T)\) se denomina en sí mismo como una serie temporal, en el sentido de que una realización se identifica con el mecanismo generador probabilístico. El objetivo del análisis de series temporales es conocer este fenómeno aleatorio subyacente a través del examen de una (y típicamente solo una) realización. Esto separa el análisis de series de tiempo de, digamos, el análisis de regresión para datos independientes.
A continuación se dan varios ejemplos que enfatizan la multitud de posibles aplicaciones del análisis de series de tiempo en diversos campos científicos.
Ejemplo 1.1.1 (números de manchas solares de W\(\ddot{\mbox{o}}\) lfer). En la Figura 1.1, el número de manchas solares (es decir, manchas oscuras visibles en la superficie del sol) que se observan anualmente se grafica contra el tiempo. El eje horizontal etiqueta el tiempo en años, mientras que el eje vertical representa los valores observados\(x_t\) de la variable aleatoria
\[ X_t=\#\mbox{ of sunspots at time $t$},\qquad t=1700,\ldots,1994. \nonumber \]
A la figura se le llama trama de serie temporal. Es un dispositivo útil para un análisis preliminar. Los números de manchas solares se utilizan para explicar las oscilaciones magnéticas en la superficie solar.
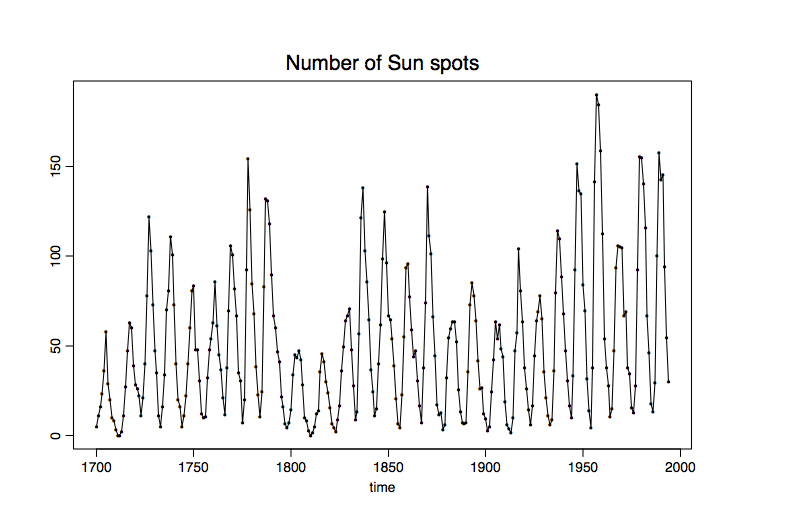
Figura 1.1: La mancha solar de Wölfer de 1700 a 1994.
Para reproducir una versión de la gráfica de series temporales de la Figura 1.1 utilizando el paquete de software libre R (las descargas están disponibles en http://cran.r-project.org), descargue el archivo sunspots.dat de la página web del curso y escriba los siguientes comandos:
> spots = leer.table (” sunspots.dat “)
> spots = ts (spots, start=1700, frecuencia=1)
> plot (spots, xlab="time”, ylab= "”, main="Number of Sun spots”)
En la primera línea, el archivo sunspots.dat se lee en los puntos del objeto, que luego en la segunda línea se transforma en un objeto de serie de tiempo usando la función ts (). El uso de start establece el valor inicial para el eje x en un número preespecificado, mientras que la frecuencia preestablece el número de observaciones para una unidad de tiempo. (Aquí: una observación anual.) Finalmente, plot es el comando de plotting estándar en R, donde xlab e ylab determinan las etiquetas para el eje x y el eje y, respectivamente, y main da el título.
Ejemplo 1.1.2 (datos de lince canadiense). La gráfica de series de tiempo en la Figura 1.2 proviene de un conjunto de datos biológicos. Contiene los rendimientos anuales de lince en subasta en Londres por la Hudson Bay Company de 1821—1934 (en una\(log_{10}\) escala). Estas son vistas como observaciones del proceso estocástico
\[ X_t=\log_{10}(\mbox{number of lynx trapped at time $1820+t$}), \qquad t=1,\ldots,114. \nonumber \]
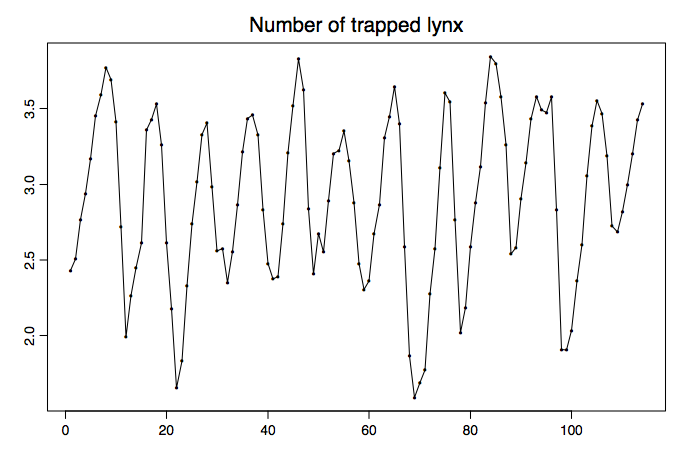
Figura 1.2: Número de lince atrapado en el distrito del río MacKenzie entre 1821 y 1934.
Los datos se utilizan como estimación del número de lince atrapados a lo largo del río MacKenzie en Canadá. Esta estimación, a su vez, suele tomarse como un proxy del verdadero tamaño poblacional del lince. Se pudo obtener una parcela similar de series de tiempo para el conejo raqueta de nieve, la principal fuente de alimento del lince canadiense, insinuando una intrincada relación depredador-presa.
Suponiendo que los datos se almacenan en el archivo lynx.dat, los comandos R correspondientes que conducen a la gráfica de series de tiempo en la Figura 1.2 son:
> lince = leer.tabla (” lynx.dat “)
> lince = ts (log10 (lince), inicio=1821, frecuencia=1)
> parcela (lince, xlab="”, ylab= "”, main="Número de lince atrapado”)
Ejemplo 1.1.3 (Letras del Tesoro). Otro campo importante de aplicación para el análisis de series temporales se encuentra en el área de las finanzas. Para cubrir los riesgos de las carteras, los inversionistas suelen utilizar tasas de interés libres de riesgo a corto plazo, como los rendimientos de letras del Tesoro a tres meses, seis meses y doce meses trazadas en la Figura 1.3. Los datos (multivariados) mostrados constan de 2 mil 386 observaciones semanales del 17 de julio de 1959 al 31 de diciembre de 1999. Aquí,
\[ X_t=(X_{t,1},X_{t,2},X_{t,3}), \qquad t=1,\ldots,2386, \nonumber \]
donde\(X_{t,1}\),\(X_{t,2}\) y\(X_{t,3}\) denotan los rendimientos de tres meses, seis meses y doce meses en el tiempo t, respectivamente. Se puede ver de la gráfica que las tres letras del Tesoro se están moviendo de manera muy similar a lo largo del tiempo, lo que implica una alta correlación entre los componentes de\(X_t\).
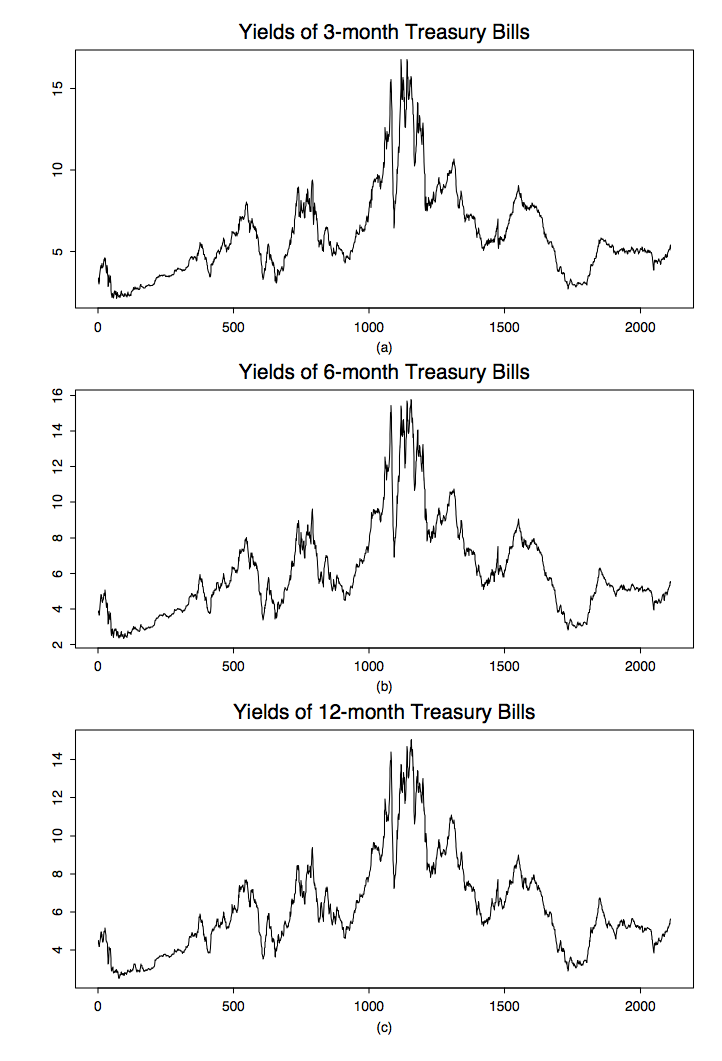
Figura 1.3: Rendimientos de letras del Tesoro del 17 de julio de 1959, al 31 de diciembre de 1999.
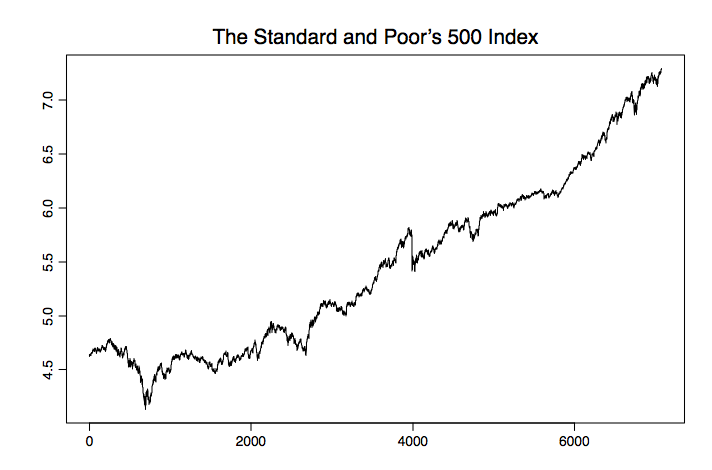
Figura 1.4: S&P 500 del 3 de enero de 1972, al 31 de diciembre de 1999.
Para producir la gráfica de series de tiempo de tres variables en la Figura 1.3, utilice el código R
> bills03 = leer.table (” bills03.dat “);
> bills06 = leer.tabla (” bills06.dat “);
> bills12 = leer.tabla (” bills12.dat “);
> par (mfrow=c (3,1))
> plot.ts (bills03, xlab=" (a)”, ylab= "”,
principal="Rendimientos de Letras de Tesorería a 3 meses”)
> plot.ts (bills06, xlab= "(b)”, ylab= "”,
main="Rendimientos de Letras del Tesoro a 6 meses”)
> plot.ts (bills12, xlab= "(c)”, ylab= "”,
main="Rendimientos de Letras del Tesoro a 12 meses”)
De nuevo se asume que los datos se pueden encontrar en los archivos correspondientes bills03.dat, bills06.dat y bills12.dat. La línea de comandos par (mfrow=c (3,1)) se utiliza para configurar los gráficos. Permite guardar tres parcelas diferentes en un mismo archivo.
Ejemplo 1.1.4 (S&P 500). El índice Standard and Poor's 500 (S&P 500) es un índice ponderado por valor basado en los precios de 500 acciones que representan aproximadamente el 70% de la capitalización bursátil estadounidense. Es un indicador económico líder y también se utiliza para cubrir carteras de mercado. La Figura 1.4 contiene los 7,076 precios diarios de cierre del S&P 500 del 3 de enero de 1972 al 31 de diciembre de 1999, en escala logaritmo natural. En consecuencia, es la gráfica de series de tiempo del proceso
\[ X_t=\ln(\mbox{closing price of S&P 500 at time $t$}), \qquad t=1,\ldots,7076. \nonumber \]
Obsérvese que la transformación logarítmica se ha aplicado para hacer que los rendimientos sean directamente comparables al porcentaje de retorno de la inversión. La gráfica de series de tiempo se puede reproducir en R usando el archivo sp500.dat
Hay innumerables otros ejemplos de todas las áreas de la ciencia. Para desarrollar una teoría capaz de manejar amplias aplicaciones, el estadístico necesita apoyarse en un marco matemático que pueda explicar fenómenos como
- tendencias (aparentes en el Ejemplo 1.1.4);
- efectos estacionales o cíclicos (aparentes en los Ejemplos 1.1.1 y 1.1.2);
- fluctuaciones aleatorias (todos los ejemplos);
- dependencia (¿todos los Ejemplos?).
El enfoque clásico tomado en el análisis de series temporales es postular que el proceso estocástico\((X_t\colon t\in T)\) investigado puede dividirse en tendencia determinista y componentes estacionales más un componente aleatorio centrado, dando lugar al modelo
\[X_t=m_t+s_t+Y_t, \qquad t\in T \tag{1.1.1} \]
donde\((m_t\colon t\in T)\) denota la función de tendencia (“componente medio”),\((s_t\colon t\in T)\) los efectos estacionales y\((Y_t\colon t\in T)\) un proceso estocástico (media cero). Una vez elegido un modelo apropiado, el estadístico podrá apuntar a
- estimar los parámetros del modelo para una mejor comprensión de las series temporales;
- predecir valores futuros, por ejemplo, para desarrollar estrategias de inversión;
- comprobando la bondad de ajuste a los datos para confirmar que el modelo elegido es apropiado.
Los procedimientos de estimación y las técnicas de predicción se tratan en detalle en capítulos posteriores de las notas. El resto de este capítulo se dedicará a introducir las clases de procesos estocásticos estricta y débilmente estacionarios (en la Sección 1.2) y a proporcionar herramientas para eliminar tendencias y componentes estacionales de una serie temporal determinada (en las Secciones 1.3 y 1.4), mientras que algunas pruebas de bondad de ajuste se presentarán en Sección 1.5.


