1.2: Series de Tiempo Estacionarias

Ajustar variables aleatorias independientes e idénticamente distribuidas a los datos es un concepto demasiado estrecho. Si bien, por un lado, permiten un tratamiento matemático algo agradable y fácil, su uso es, por otro lado, a menudo difícil de justificar en las aplicaciones. Por lo tanto, nuestro objetivo es introducir un concepto que mantenga algunas de las propiedades deseables de variables aleatorias independientes e idénticamente distribuidas (“regularidad”), pero que también amplíe considerablemente la clase de procesos estocásticos para elegir al permitir la dependencia así como las distribuciones variables. La dependencia entre dos variables aleatorias\(X\) y generalmente\(Y\) se mide en términos de\(covariance\)\(function\)

\[ Cov(X,Y)=E\big[(X-E[X])(Y-E[Y])\big] \nonumber \]

y el\(correlation\)\(function\)

\[ Corr(X,Y)=\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}. \nonumber \]

Con estas notaciones a la mano, se pueden introducir las clases de procesos estocásticos estricta y débilmente dependientes.

Definición 1.2.1 (Estricta Estacionariedad). Un proceso estocástico (\(X_t\colon t\in T\)) se llama estrictamente estacionario si, para todos\(t_1,...,t_n \in T\) y\(h\) tal que\(t_1+h,...,t_n+h\in T\), sostiene que
\ [(
X_ {t_1},\ ldots, X_ {t_n})
\ stackrel {\ cal D} {=}
(X_ {t_1+h},\ ldots, X_ {t_n+h}).
\ nonumber\] Es
decir, las llamadas distribuciones finito-dimensionales del proceso son invariantes bajo los cambios de tiempo. Aquí\(=^{\cal D}\) indica igualdad en la distribución.

La definición en términos de la distribución finito-dimensional se puede reformular de manera equivalente en términos de las igualdades de función de distribución conjunta acumulativa

\[ P(X_{t_1}\leq x_1,\ldots,X_{t_n}\leq x_n)=P(X_{t_1+h}\leq x_1,\ldots,X_{t_n+h}\leq x_n) \nonumber \]

manteniéndose fiel para todos\(x_1,...,x_n\in\mathbb{R}\),\(t_1,...,t_n\in T\) y\(h\) tal que\(t_1+h,...,t_n+h\in T\). Esto puede ser bastante difícil de verificar para una serie temporal determinada, especialmente si el mecanismo generador de una serie temporal está lejos de ser simple, ya que hay que estimar demasiados parámetros del modelo a partir de los datos disponibles, haciendo imposibles declaraciones estadísticas concisas. Una posible excepción es proporcionada por el caso de variables aleatorias independientes e idénticamente distribuidas.

Para sortear estas dificultades, un analista de series temporales normalmente solo especificará los momentos de primer y segundo orden de las distribuciones conjuntas. Hacerlo entonces lleva a la noción de estacionariedad débil.

Definición 1.2.2 (Estacionariedad débil). Un proceso estocástico\((X_t\colon t\in T)\) se llama débilmente estacionario si

• los segundos momentos son finitos:\(E[X_t^2]<\infty\) for all \(t\in T\);
• los medios son constantes:\(E[X_t]=m\) para todos\(t\in T\);
• la covarianza de\(X_t\) y\(X_{t+h}\) depende\(h\) solo de:

\[ \gamma(h)=\gamma_X(h)=Cov(X_t,X_{t+h}), \qquad h\in T \mbox{ such that } t+h\in T, \nonumber \]
es independiente de\(t\in T\) y se llama la función de autocovarianza (ACVF). Además,
\[ \rho(h)=\rho_X(h)=\frac{\gamma(h)}{\gamma(0)},\qquad h\in T, \nonumber \]
se llama la función de autocorrelación (ACF).

OBSERVACIÓN 1.2.1. Si\((X_t: t\in T)\)) es un proceso estocástico estrictamente estacionario con segundos momentos finitos, entonces también es débilmente estacionario. Lo contrario no es necesariamente cierto. Si\((X_t\colon t\in T)\), sin embargo, es débilmente estacionario y gaussiano, entonces también es estrictamente estacionario. Recordemos que un proceso estocástico se llama gaussiano si, para alguno\(t_1,...,t_n\in T\), el vector aleatorio\((X_{t_1},...,X_{t_n})\) es multivariado distribuido normalmente.

Esta sección se concluye con ejemplos de procesos estocásticos estacionarios y no estacionarios.

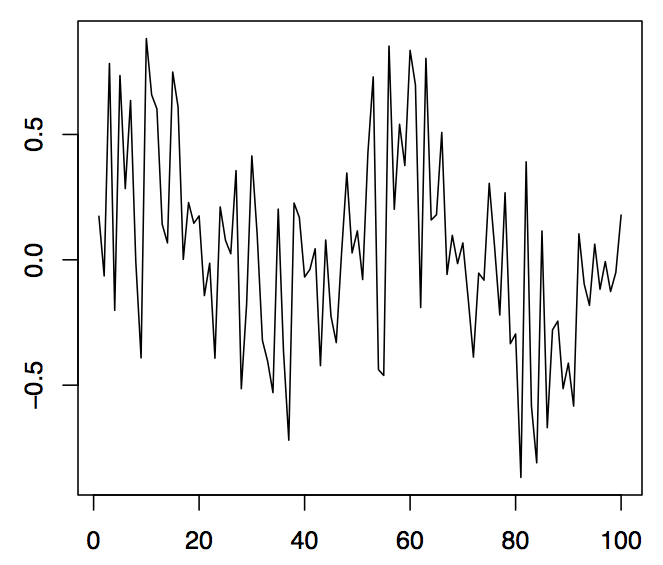
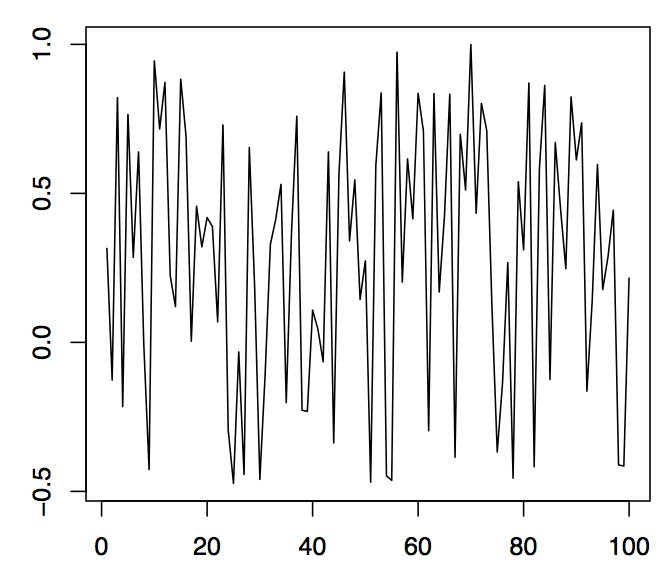
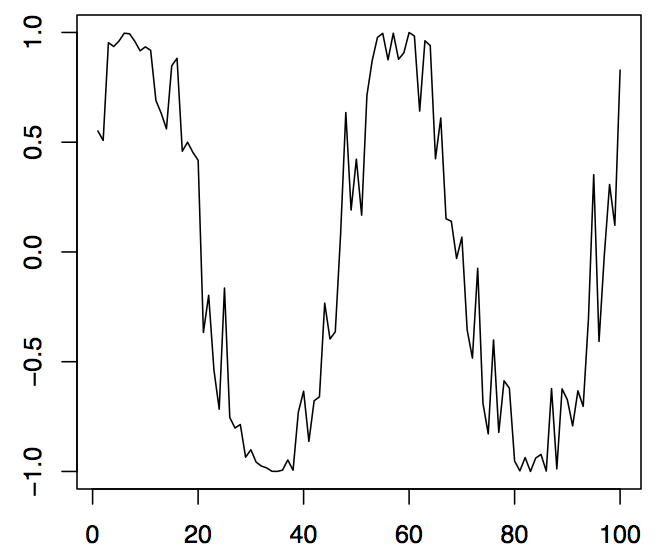
• Figura 1.5:100 valores simulados de la serie temporal cíclica (panel izquierdo), la amplitud estocástica (panel medio) y la parte sinusoidal (panel derecho).

Ejemplo 1.2.1 (Ruido Blanco). Dejar\((Z_t\colon t\in\mathbb{Z})\) ser una secuencia de variables aleatorias de valor real, por pares no correlacionadas con\(E[Z_t]=0\) y\(0<Var(Z_t)=\sigma^2<\infty\) para todos\(t\in\mathbb{Z}\). Entonces\((Z_t\colon t\in Z)\) se llama ruido blanco, abreviado por\((Z_t\colon t\in\mathbb{Z})\sim{\rm WN}(0,\sigma^2)\). Define un proceso centrado, débilmente estacionario con ACVF y ACF dados por
\ [
\ gamma (h) =\ left\ {\ begin {array} {r@ {\ quad\;} l}\ sigma^2, & h=0,\\ 0, & h\ not=0,\ end {array}\ right.
\ qquad\ mbox {y}\ qquad
\ rho (h) =\ left\ {\ begin {array} {r@ {\ quad\;} l} 1, & h=0,\\ 0, & h\ no=0,\ end {array}\ right.
\ nonumber\]
respectivamente. Si los\((Z_t\colon t\in\mathbb{Z})\) son además independientes e idénticamente distribuidos, se les llama ruido iid, en breve\((Z_t\colon t\in\mathbb{Z})\sim{\rm IID}(0,\sigma^2)\). El panel izquierdo de la Figura 1.6 muestra 1000 observaciones de una secuencia de ruido iid\((Z_t\colon t\in\mathbb{Z})\) basada en variables aleatorias normales estándar. Los comandos R correspondientes para producir la gráfica son

> z = rnorm (1000,0,1)
> plot.ts (z, xlab= "”, ylab= "”, main= "”)

El comando rnorm simula aquí 1000 variables aleatorias normales con media 0 y varianza 1. Hay varios generadores de variables aleatorias incorporados en R como las funciones runif (n, a, b) y rbinom (n, m, p) que simulan los\(n\) valores de una distribución uniforme en el intervalo\((a,b)\) y una distribución binomial con parámetro de repetición\(m\) y éxito probabilidad\(p\), respectivamente.

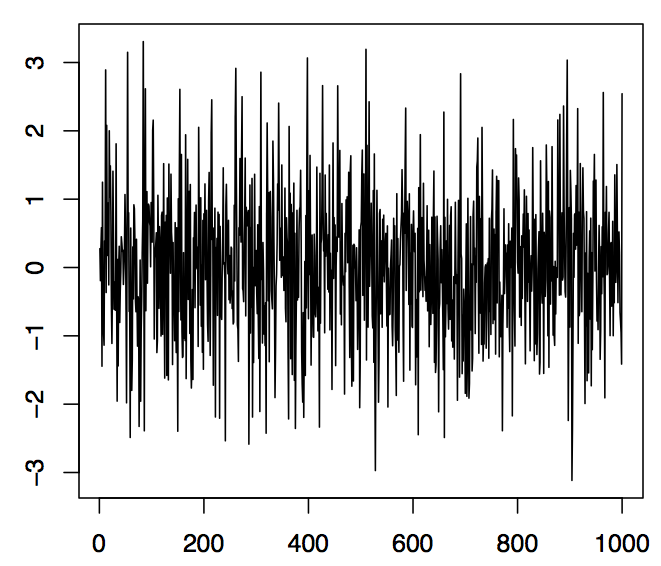
Figura 1.6:1000 valores simulados de ruido iid N (0, 1) (panel izquierdo) y una caminata aleatoria con innovaciones iid N (0, 1) (panel derecho).

Ejemplo 1.2.2 (Series de Tiempo Cíclicas). Dejar\(A\) y\(B\) ser variables aleatorias no correlacionadas con media cero y varianzas\(Var(A)=Var(B)=\sigma^2\), y dejar\(\lambda\in\mathbb{R}\) ser un parámetro de frecuencia. Define
\ [
x_t=A\ cos (\ lambda t) +B\ sin (\ lambda t),\ qquad t\ in\ mathbb {R}.
\ nonumber\]
El proceso estocástico resultante\((X_t\colon t\in\mathbb{R})\) es entonces débilmente estacionario. Ya que\(\sin(\lambda t+\varphi)=\sin(\varphi)\cos(\lambda t)+\cos(\varphi)\sin(\lambda t)\), el proceso puede representarse como
\ [
x_t=R\ sin (\ lambda t+\ varphi),\ qquad t\ in\ mathbb {R},
\ nonumber\]
así\(R\) es la amplitud estocástica y\(\varphi\in[-\pi,\pi]\) la fase estocástica de una sinusoide. Algunos cálculos muestran que uno debe tener\(A=R\sin(\varphi)\) y\(B=R\cos(\varphi)\). En el panel izquierdo de la Figura 1.5, se\((X_t)_{t\in \mathbb{Z}}\) muestran 100 valores observados de una serie. En ella,\(\lambda=\pi/25\) se utilizó, mientras que\(R\) y\(\varphi\) fueron variables aleatorias distribuidas uniformemente en el intervalo\((-.5,1)\) y\((0,1)\), respectivamente. El panel central muestra la realización de\(R\), el panel derecho la realización de\(\sin(\lambda t+\varphi)\). El uso de series temporales cíclicas conlleva grandes ventajas cuando se tienen que modelar efectos estacionales, como los fenómenos recurrentes anuales. Se pueden aplicar los siguientes comandos R:

> t = 1:100; R = runif (100, -.5,1); phi = runif (100,0,1); lambda = pi/25
> cyc = R*sin (lambda*t+phi)
> trazos.ts (cyc, xlab= "”, ylab= "”)

Esto produce el panel izquierdo de la Figura 1.5. Los paneles medio y derecho siguen de manera similar.

Ejemplo 1.2.3 (Paseo Aleatorio). Vamos\((Z_t\colon t\in\mathbb{N})\sim{\rm WN}(0,\sigma^2)\). Dejar\(S_0=0\) y
\ [
s_t=z_1+\ lDots+z_t,\ qquad t\ in\ mathbb {N}.
\ nonumber\]
El proceso estocástico resultante\((S_t\colon t\in\mathbb{N}_0)\) se llama caminata aleatoria y es la serie de tiempo no estacionaria más importante. En efecto, sostiene aquí que, para\(h>0\),
\ [
Cov (s_t, S_ {t+h}) =Cov (s_t, s_t+r_ {t, h}) =t\ sigma^2,
\ nonumber\]
donde\(R_{t,h}=Z_{t+1}+\ldots+Z_{t+h}\), y el ACVF obviamente depende de\(t\). En R, se puede construir una caminata aleatoria, por ejemplo, con el siguiente comando simple que utiliza las 1000 observaciones normales almacenadas en la matriz z del Ejemplo 1.2.1.

> rw = cumsum (z)
La función cumsum toma como entrada una matriz y devuelve como salida una matriz de la misma longitud que contiene como su j ésima entrada la suma de las j primeras entradas de entrada. La gráfica resultante de series de tiempo se muestra en el panel derecho de la Figura 1.6.

El capítulo 3 analiza en detalle los llamados procesos de promedio móvil autorregresivos que se han convertido en un bloque central en el análisis de series de tiempo. Se construyen a partir de secuencias de ruido blanco mediante la aplicación de un conjunto de ecuaciones de diferencia estocásticas similares a las que definen la caminata aleatoria\((S_t\colon t\in\mathbb{N}_0)\) del Ejemplo 1.2.3.

En general, los verdaderos parámetros de un proceso estocástico estacionario\((X_t\colon t\in T)\) son desconocidos para el estadístico. Por lo tanto, tienen que ser estimados a partir de una realización\(x_1,...,x_n\). Aquí se utilizará el siguiente conjunto de estimadores. La media muestral de\(x_1,...,x_n\) se define como
\ [
\ bar {x} =\ frac 1n\ sum_ {t=1} ^nx_t.
\ nonumber\]
La función de autocovarianza de muestra (ACVF de muestra) viene dada por
\ begin {ecuación}\ label {eq:1.2.1}
\ hat { \ gamma} (h) =
\ frac 1n\ suma_ {t=1} ^ {n-h} (x_ {t+h} -\ bar {x}) (x_t-\ bar {x}),
\ qquad h=0,1,\ lpuntos, n-1.
\ end {ecuación}
Finalmente, la función de autocorrelación de muestra (muestra ACF) es

\ [\ hat {\ rho} (h) =\ frac {\ hat {\ gamma} (h)} {\ hat {\ gamma} (0)},
\ qquad h=0,1,\ ldots, n-1.
\ nonumber\]

Ejemplo 1.2.4. Dejar\((Z_t\colon t\in\mathbb{Z})\) ser una secuencia de variables aleatorias estándar independientes normalmente distribuidas (ver el panel izquierdo de la Figura 1.6 para una realización típica de tamaño n = 1,000). Entonces, claramente,\(\gamma(0)=\rho(0)=1\) y\(\gamma(h)=\rho(h)=0\) cuando sea\(h\not=0\). En el cuadro 1.1 se indican los valores estimados correspondientes\(\hat{\gamma}(h)\) y\(\hat{\rho}(h)\) para\(h=0,1,\ldots,5\).

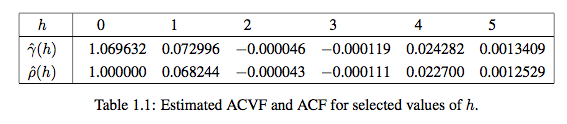
Los valores estimados son todos muy cercanos a los verdaderos, lo que indica que los estimadores funcionan razonablemente bien para n = 1,000. Efectivamente se puede demostrar que son asintóticamente imparciales y consistentes. Además, las autocorrelaciones muestrales\(\hat{\rho}(h)\) son aproximadamente normales con media y varianza cero\(1/1000\). Véase también Teorema 1.2.1 a continuación. En R, la función acf se puede utilizar para calcular el ACF de muestra.

Teorema 1.2.1. Dejar\((Z_t\colon t\in\mathbb{Z})\sim{\rm WN}(0,\sigma^2)\) y dejar\(h\not=0\). Bajo un conjunto general de condiciones, se sostiene que el ACF muestral al rezago\(h\)\(\hat{\rho}(h)\), es para grandes\(n\) aproximadamente distribuido normalmente con media cero y varianza 1/n.

El Teorema 1.2.1 y el Ejemplo 1.2.4 sugieren un primer método para evaluar si un conjunto de datos dado puede modelarse convenientemente mediante una secuencia de ruido blanco: para una secuencia de ruido blanco, aproximadamente el 95% de los ACF de muestra deben estar dentro del intervalo de confianza\(\pm2/\sqrt{n}\). Usando los archivos de datos en la página web del curso, se pueden calcular con R los ACF de muestra correspondientes para verificar la blancura de las series temporales subyacentes. Las propiedades del ACF muestral se revisan en el Capítulo 2.

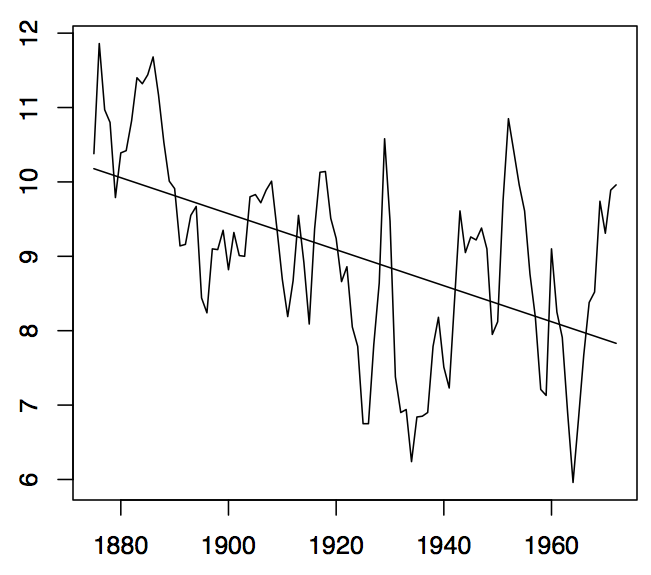
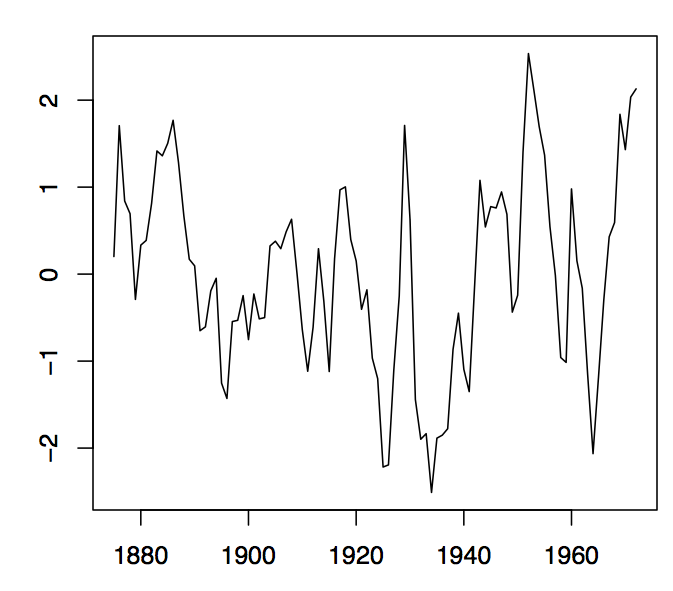
• Figura1.7: Niveles anuales de agua del Lago Huron (panel izquierdo) y la parcela residual obtenida al ajustar una tendencia lineal a los datos (panel derecho).