3.3: El PACF de un proceso de ARMA Causal
- Page ID
- 148654
En esta sección se introduce la función de autocorrelación parcial (PACF) para evaluar aún más la estructura de dependencia de los procesos estacionarios en general y los procesos causales ARMA en particular. Para empezar, calculemos el ACVF de un proceso de promedio móvil de orden\(q\)
Ejemplo\(\PageIndex{1}\): The ACVF of an MA(\(q\)) process
Let\((X_t\colon t\in\mathbb{Z})\) Ser un proceso MA (\(q\)) especificado por el polinomio\(\theta(z)=1+\theta_1z+\ldots+\theta_qz^q\). Entonces, dejando\(\theta_0=1\), sostiene que
\[ E[X_t]=\sum_{j=0}^q\theta_jE[Z_{t-j}]=0. \nonumber \]
Solución
Para calcular el ACVF, supongamos que\(h\geq 0\) y escriba
\ begin {align*}
\ gamma (h) &= Cov (X_ {t+h}, X_ {t}) =E [X_ {t+h} X_ {t}]\\ [.2cm]
&=E\ izquierda [\ izquierda (\ suma_ {j=0} ^q\ TheTa_jz_ {t+h-j}\ derecha)\ izquierda (\ sum_ {j=0} ^q\ TheTa_JZ_ {t+h-j}\ derecha)
\ izquierda (\ sum_ {{k=0} ^q\ theta_kz_ {t-k}\ derecha)\ derecha]\\ [.2cm]
&=\ suma_ {j=0} ^q\ suma_ {k=0} ^q\ theta_j\ theta_ke [Z_ {t+h-j} Z_ {t-k}]\\ [ .2cm]
&=\ left\ {\ begin {array} {l@ {\ qquad} r}
\ displaystyle\ sigma^2\ sum_ {k=0} ^ {q-h}\ theta_ {k+h}\ theta_k,
& 0\ leq h\ leq q.\\ [.2cm]
0, & h>q.
\ end {array} derecha\.
\ end {alinear*}
El resultado aquí es una generalización del caso MA (1), el cual fue tratado en el Ejemplo 3.2.3. También es un caso especial del proceso lineal en el Ejemplo 3.1.4. La estructura del ACVF para procesos MA indica una estrategia posible para determinar en la práctica el orden desconocido\(q\): graficar el ACF de la muestra y seleccionar como orden\(q\) el mayor rezago de tal manera que\(\rho(h)\) sea significativamente diferente de cero.
Si bien el ACF de muestra puede revelar potencialmente el verdadero orden de un proceso de MA, lo mismo ya no es cierto en el caso de los procesos AR. Incluso para las series de tiempo AR (1) se ha mostrado en el Ejemplo 3.2.1 que su ACF\(\rho(h)=\phi^{|h|}\) es distinto de cero para todos los rezagos. Como motivación adicional, sin embargo, discutimos el siguiente ejemplo.
Ejemplo 3.3.2
Dejar\((X_t\colon t\in\mathbb{Z})\) ser un proceso de AR causal (1) con parámetro\(|\phi|<1\). Sostiene que
\ [\ gamma (2) =Cov (X_2, X_ {0})
=Cov (\ phi^2x_ {0} +\ phi Z_ {1} +Z_2, X_ {0})
=\ phi^2\ gamma (0)\ no=0. \ nonumber\]
Para romper la dependencia lineal entre\(X_0\) y\(X_2\), restar\(\phi X_1\) de ambas variables. Cálculo de los rendimientos de covarianza resultantes
\[ Cov(X_2-\phi X_{1},X_0-\phi X_1)= Cov(Z_2,X_0-\phi X_1)=0, \nonumber \]
ya que, debido a la causalidad de este proceso AR (1),\(X_0-\phi X_1\) es una función de\(Z_{1},Z_0,Z_{-1},\ldots\) y por lo tanto no está correlacionada con\(X_2-\phi X_1=Z_2\).
El ejemplo anterior motiva la siguiente definición general.
Definición 3.3.1 Función de autocorrelación parcial
Dejar\((X_t\colon t\in\mathbb{Z})\) ser un proceso estocástico débilmente estacionario con media cero. Luego, la secuencia\((\phi_{hh}\colon h\in\mathbb{N})\) dada por
\ begin {align*}
\ phi_ {11} &=\ rho (1) =Corr (X_1, X_0),\\ [.2cm]
\ phi_ {hh} &=Corr (x_h-x_h^ {h-1}, X_0-X_0^ {h-1}),\ qquad
h\ geq 2,
\ end {align*}
se llama la función de autocorrelación parcial (PACF) de\((X_t\colon t\in\mathbb{Z})\).
En ella,
\ begin {align*}
x_h^ {h-1} &=\ mbox {regresión de $x_h$ on
} (X_ {h-1},\ ldots, X_1)\\ [.2cm]
&=\ beta_1x_ {h-1} +\ beta_2x_ {h-2} +\ ldots+\ beta_ {h-1} X_1\ [.3cm]
X_0^ {h-1} &=\ mbox {regresión de $X_0$ en
} (X_1,\ ldots, X_ {h-1})\\ [.2cm]
&=\ beta_1x_1+\ beta_2x_2+\ ldots+\ beta_ {h-1} X_ {h-1}.
\ end {alinear*}
Observe que no hay coeficiente de intercepción\(\beta_0\) en los parámetros de regresión, ya que se supone que\(E[X_t]=0\). El siguiente ejemplo demuestra cómo calcular los parámetros de regresión en el caso de un proceso AR (1).
Ejemplo 3.3.3 PACF de un proceso AR (1)]
Si\((X_t\colon t\in\mathbb{Z})\) es un proceso de AR causal (1), entonces\(\phi_{11}=\rho(1)=\phi\). Para calcular\(\phi_{22}\), calcular primero\(X_2^1=\beta X_1\), es decir\(\beta\). Este coeficiente se determina minimizando el error cuadrático medio entre\(X_2\) y\(\beta X_1\):
\[ E[X_2-\beta X_1]^2=\gamma(0)-2\beta\gamma(1)+\beta^2\gamma(0) \nonumber \]
que se minimiza por\(\beta=\rho(1)=\phi\). (Esto sigue fácilmente tomando la derivada y poniéndola a cero). Por lo tanto\(X_2^1=\phi X_1\). De igual manera, se calcula\(X_0^1=\phi X_1\) y se deduce del Ejemplo 3.3.2 que\(\phi_{22}=0\). Efectivamente todos los rezagos\(h\geq 2\) del PACF son cero.
De manera más general, considere brevemente un proceso de AR causal (\(p\)) dado por\(\phi(B)X_t=Z_t\) with\(\phi(z)=1-\phi_1z-\ldots-\phi_pz^p\).
Entonces, para\(h>p\),
\[ X_h^{h-1}=\sum_{j=1}^p\phi_jX_{h-j} \nonumber \]
y consecuentemente
\[ \phi_{hh}=Corr(X_h-X_h^{h-1},X_0-X_0^{h-1}) = Corr(Z_h,X_0-X_0^{h-1})=0 \nonumber \]
si\(h>p\) por causalidad (el mismo argumento usado en el Ejemplo 3.3.2 también se aplica aquí). Observe, sin embargo, que no\(\phi_{hh}\) es necesariamente cero si\(h\leq p\). Lo anterior sugiere que la versión de muestra del PACF puede ser utilizada para identificar el orden de un proceso autorregresivo a partir de datos: usar como\(p\) el mayor retraso\(h\) tal que\(\phi_{hh}\) es significativamente diferente de cero.
Por otro lado, para un proceso MA (\(q\)) invertible, se puede escribir\(Z_t=\pi(B)X_t\) o, de manera equivalente,
\[ X_t=-\sum_{j=1}^\infty\pi_jX_{t-j}+Z_t \nonumber \]
lo que demuestra que el PACF de un proceso MA (\(q\)) será distinto de cero para todos los rezagos, ya que para una regresión ``perfecta” habría que usar todas las variables pasadas en\((X_s\colon s<t)\) lugar de solo la cantidad\(X_t^{t-1}\) dada en la Definición 3.3.1.
En resumen, el PACF invierte el comportamiento del ACVF para procesos autorregresivos y de promedio móvil. Mientras que estos últimos tienen un ACVF que desaparece después del retraso\(q\) y un PACF que no es cero (aunque en descomposición) para todos los rezagos, los procesos AR tienen un ACVF que no es cero (aunque en descomposición) para todos los rezagos pero un PACF que desaparece después del retraso\(p\).
ACVF (ACF) y PACF por lo tanto proporcionan herramientas útiles para evaluar la dependencia de procesos ARMA dados. Si el ACVF estimado (el PACF estimado) es esencialmente cero después de algún retraso de tiempo, entonces la serie temporal subyacente se puede modelar convenientemente con un proceso MA (AR), y no se tiene que ajustar ninguna secuencia general de ARMA. Estas conclusiones se resumen en la Tabla 3.3.1
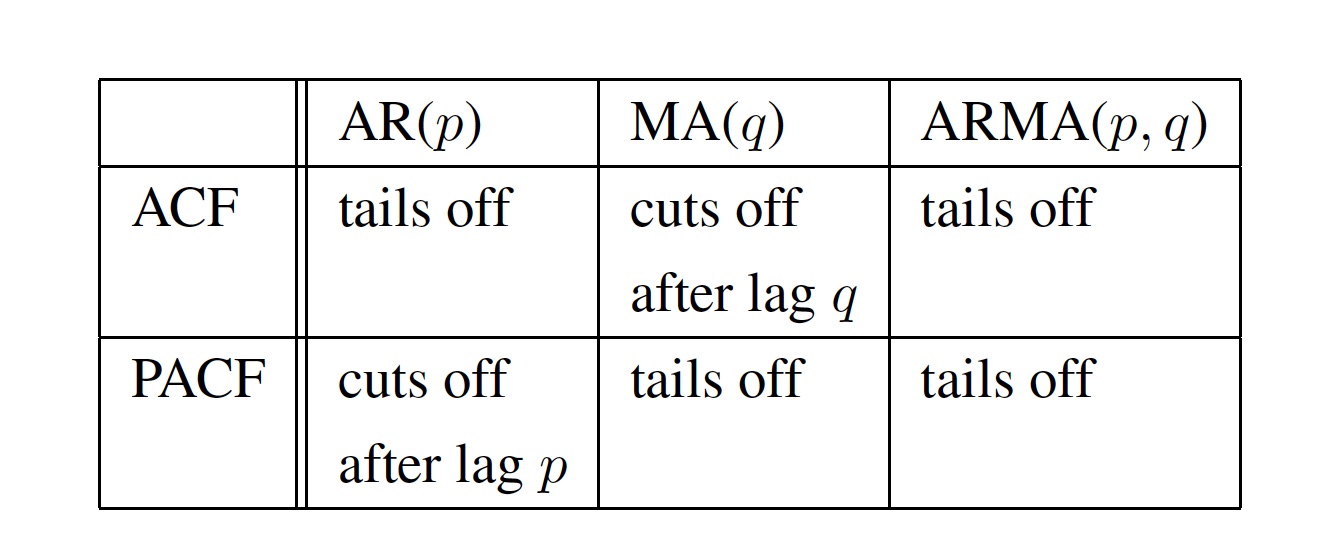
Cuadro 3.1: Comportamiento de ACF y PACF para los procesos AR, MA y ARMA.
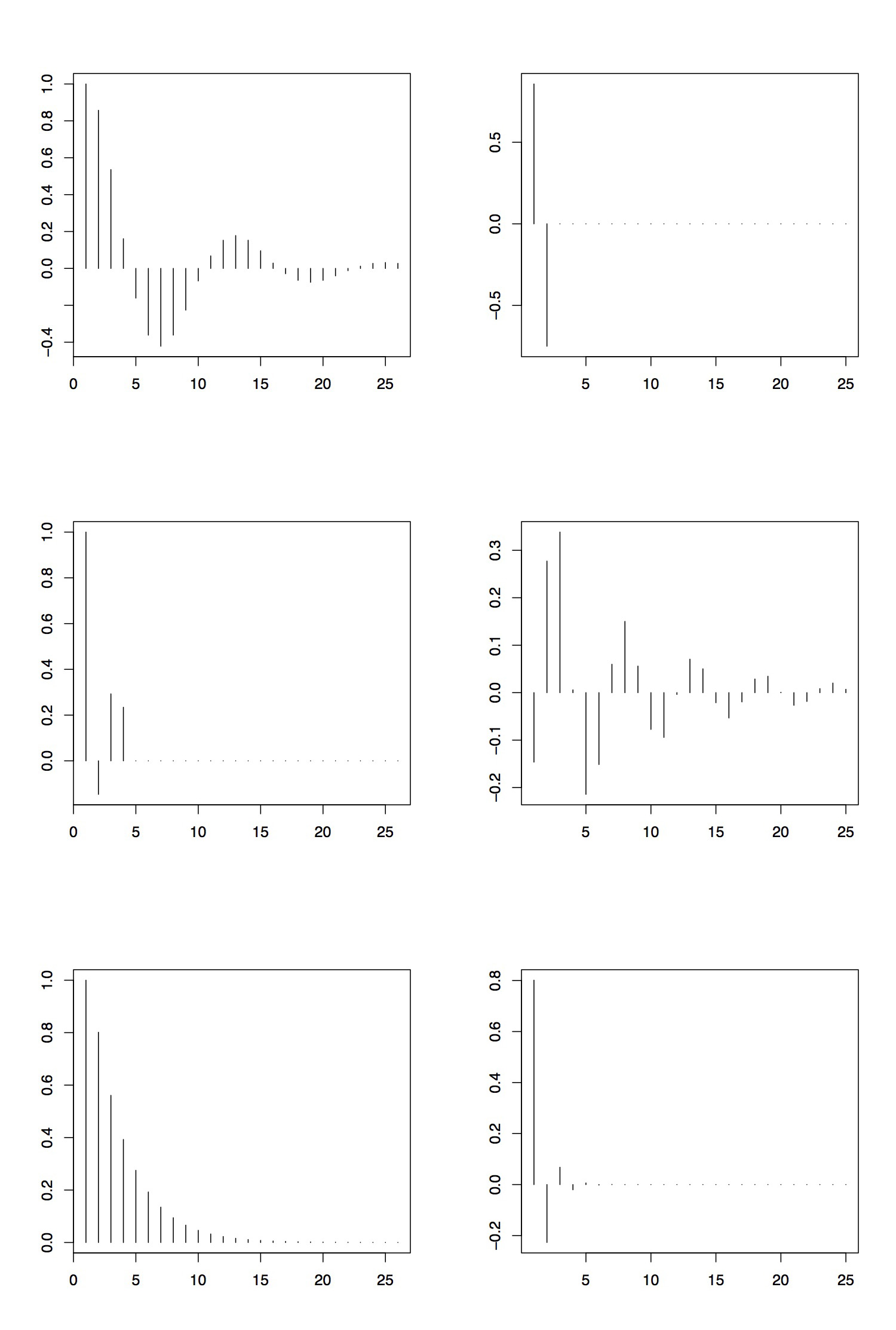
Ejemplo 3.3.4
La Figura 3.5 recoge los ACF y PACF de tres procesos ARMA. El panel superior se toma del proceso AR (2) con parámetros\(\phi_1=1.5\) y\(\phi_2=-.75\). Se puede observar que el ACF se apaga y muestra un comportamiento cíclico (tenga en cuenta que el polinomio autorregresivo correspondiente tiene raíces complejas). El PACF, sin embargo, corta después del rezago 2. Así, inspeccionando ACF y PACF, especificaríamos correctamente el orden del proceso AR.
El panel central muestra el ACF y PACF del proceso MA (3) dado por los parámetros\(\theta_1=1.5\),\(\theta_2=-.75\) y\(\theta_3=3\). Las parcelas lo confirman\(q=3\) debido a que el ACF corta después del lag 3 y el PACF fracasa.
Finalmente, el panel inferior muestra el ACF y PACF del proceso ARMA (1,1) del Ejemplo 3.2.4. Aquí, la evaluación es mucho más difícil. Mientras que el ACF fracasa como se predijo (ver Cuadro 3.1), el PACF básicamente corta después del retraso 4 o 5. Esto podría llevar a la conclusión equivocada de que el proceso subyacente es en realidad un proceso AR de orden 4 o 5. (La razón de este comportamiento radica en el hecho de que la dependencia en este proceso ARMA (1,1) en particular puede aproximarse bien por la de una serie de tiempo AR (4) o AR (5).)
Para reproducir las gráficas en R, puede usar los comandos
>ar2.acf=armaACF (ar=c (1.5, -.75), ma=0, 25)
>ar2.pacf=armaACF (ar=c (1.5, -.75), ma=0, 25, PACF=T)
para el proceso AR (2). Los otros dos casos se derivan de adaptaciones directas de este código.
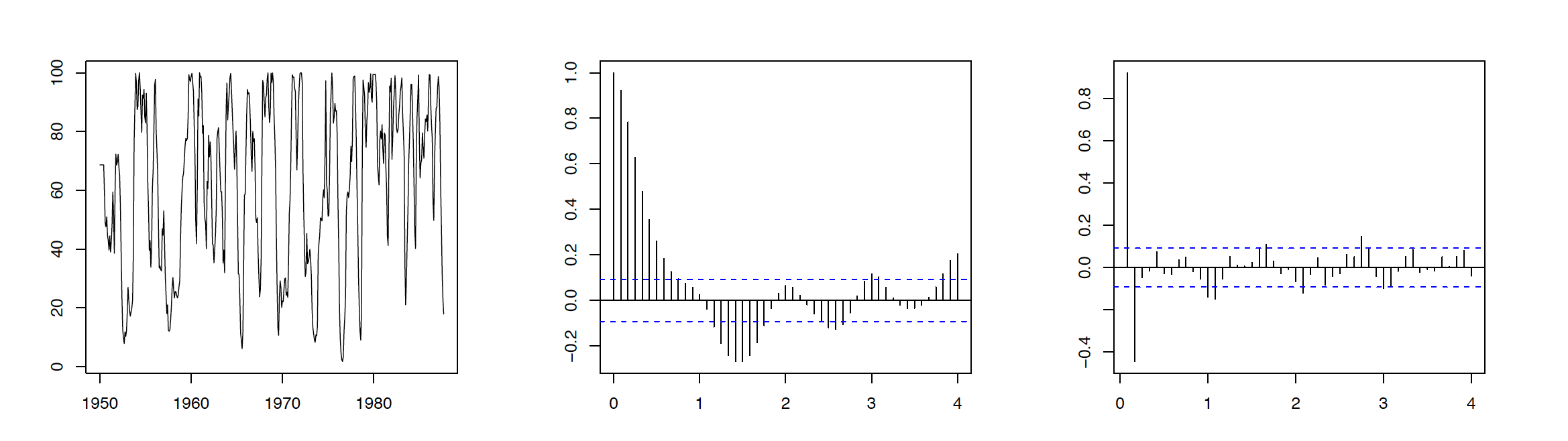
Ejemplo 3.3.5 Serie de Reclutamiento
Los datos considerados en este ejemplo consisten en 453 meses de reclutamiento observado (número de peces nuevos) en cierta parte del Océano Pacífico recolectados a lo largo de los años 1950—1987. La gráfica de series de tiempo correspondiente se da en el panel izquierdo de la Figura 3.6. Los ACF y PACF correspondientes mostrados en el panel medio y derecho de la misma figura recomiendan ajustar un proceso AR de orden\(p=2\) a los datos de reclutamiento. Suponiendo que los datos están en rec, el código R a reproducir Figura 3.6 es
> rec = ts (rec, inicio=1950, frecuencia=12)
> parcela (rec, xlab= "”, ylab= "”)
> acf (rec, lag=48)
> pacf (rec, lag=48)
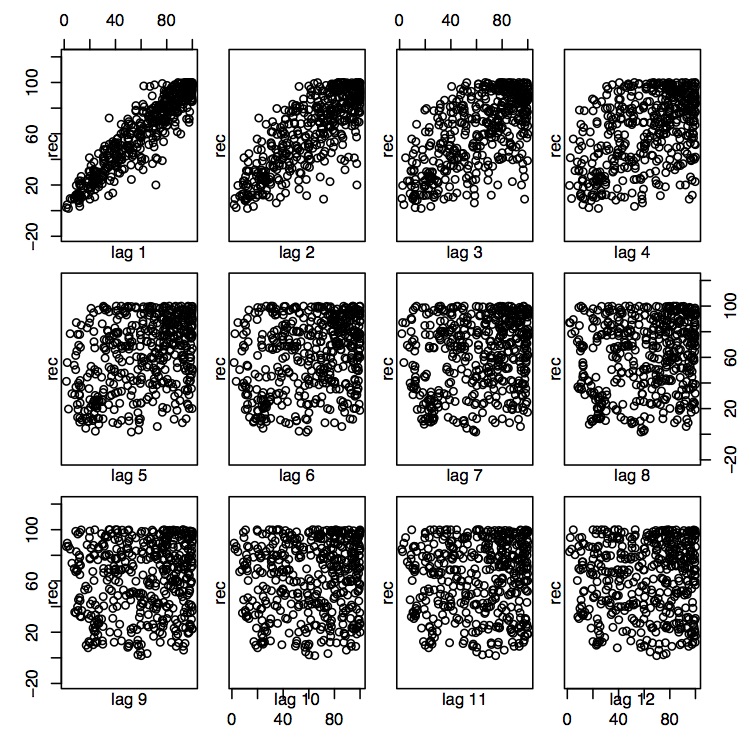
Esta afirmación también es congruente con las tramas de dispersión que relacionan el reclutamiento actual con el reclutamiento pasado en varios rezagos de tiempo, a saber\(h=1,\ldots,12\). Para los rezagos 1 y 2, parece haber una fuerte relación lineal, mientras que ya no es así para\(h\geq 3\). Los comandos R correspondientes son
> lag.plot (rec, lags=12, layout=c (3,4), diag=F)
Denotar por\(X_t\) el reclutamiento en el momento\(t\). Para estimar los parámetros AR (2), ejecutar una regresión sobre los tripletes de datos observados incluidos en el conjunto\( (x_t,x_ t-1,x_ t-2)\colon j=3,\ldots,453 \) para ajustarse a un modelo de la forma
\[ X_t=\phi_0+\phi_1X_ t-1+\phi_2X_ t-2+Z_t, \qquad t=3,\ldots,453, \nonumber \]
donde\((Z_t)\sim\mathrm WN(0,\sigma^2)\). Esta tarea se puede realizar en R de la siguiente manera.
> fit.rec = ar.ols (rec, AIC=F, orden.max=2, demean=F, intercept=T)
Estas estimaciones se pueden evaluar con el comando {\ tt fit.rec} y los errores estándar correspondientes con\(\tt fit.rec{\$}asy.se\). Aquí se obtienen las estimaciones de parámetros\(\hat{\phi}_0=6.737(1.111)\)\(\hat{\phi}_1=1.3541(.042)\),,\(\hat{\phi}_2=-.4632(.0412)\) y\(\hat{\sigma}^2=89.72\). Los errores estándar se dan entre paréntesis.


