3.2: Causalidad e invertibilidad
- Page ID
- 148651
Si bien un proceso de orden promedio móvil siempre\(q\) será estacionario sin condiciones sobre los coeficientes\(\theta_1\),,\(\ldots\)\(\theta_q\), se requieren algunos pensamientos más profundos en el caso de los procesos AR (\(p\)) y ARMA (\(p,q\)). Por simplicidad, comenzamos por investigar el proceso autorregresivo del orden uno, que viene dado por las ecuaciones\(X_t=\phi X_{t-1}+Z_t\) (escritura\(\phi=\phi_1\)). Las iteraciones repetidas producen que
\[X_t =\phi X_{t-1}+Z_t =\phi^2X_{t-2}+Z_t+\phi Z_{t-1}=\ldots =\phi^NX_{t-N}+\sum_{j=0}^{N-1}\phi^jZ_{t-j}. \nonumber \]
Dejando\(N\to\infty\), ahora podría demostrarse que, con probabilidad uno,
\[ X_t=\sum_{j=0}^\infty\phi^jZ_{t-j} \tag{3.2.2} \]
es la solución débilmente estacionaria a las ecuaciones AR (1), siempre que\(|\phi|<1\). These calculations would indicate moreover, that an autoregressive process of order one can be represented as linear process with coefficients \(\psi_j=\phi^j\).
Ejemplo\(\PageIndex{1}\): Mean and ACVF of an AR(1) process
Dado que un proceso autorregresivo del orden uno ha sido identificado como un ejemplo de un proceso lineal, se puede determinar fácilmente su valor esperado como
\[ E[X_t]=\sum_{j=0}^\infty\phi^jE[Z_{t-j}]=0, \qquad t\in\mathbb{Z}. \nonumber \]
Para la ACVF, se obtiene que
\ begin {alinear*}
\ gamma (h)
&= {\ rm Cov} (X_ {t+h}, x_t)\\ [.2cm]
&=E\ left [\ sum_ {j=0} ^\ infty\ phi^jz_ {t+h-j}\ suma_ {k=0} ^\ infty\ phi^Kz_ {t-k}\ derecha]\\ [.2cm]
&=\ sigma^2\ suma_ {k=0} ^\ infty\ phi^ {k+h}\ phi^ {k}
=\ sigma^2\ phi^h\ suma_ {k=0} ^\ infty\ phi ^ {2k}
=\ frac {\ sigma^2\ phi^h} {1-\ phi^2},
\ end {alinear*}
donde\(h\geq 0\). This determines the ACVF for all \(h\) using that \(\gamma(-h)=\gamma(h)\). It is also immediate that the ACF satisfies \(\rho(h)=\phi^h\). See also Example 3.1.1 for comparison.
Ejemplo\(\PageIndex{2}\): Nonstationary AR(1) processes
En el Ejemplo 1.2.3 hemos introducido la caminata aleatoria como una serie de tiempo no estacionaria. También se puede ver como un proceso AR (1) no estacionario con parámetro\(\phi=1\). En general, los procesos autorregresivos de orden uno con coeficientes se\(|\phi|>1\) denominan {\ it explosivo}\/porque no admiten una solución débilmente estacionaria que pudiera expresarse como un proceso lineal. No obstante, se podrá proceder de la siguiente manera. Reescribir las ecuaciones definitorias de un proceso AR (1) como
\[ X_t=-\phi^{-1}Z_{t+1}+\phi^{-1}X_{t+1}, \qquad t\in\mathbb{Z}. \nonumber \]
Aplica ahora las mismas iteraciones que antes para llegar a
\[ X_t=\phi^{-N}X_{t+N}-\sum_{j=1}^N\phi^{-j}Z_{t+j},\qquad t\in\mathbb{Z}. \nonumber \]
Obsérvese que en el caso débilmente estacionario, la presente observación ha sido descrita en términos de innovaciones pasadas. Sin embargo, la representación en la última ecuación contiene solo observaciones futuras con retardos de tiempo mayores que el tiempo presente\(t\). Desde el punto de vista estadístico esto no tiene mucho sentido, aunque por argumentos idénticos a los anteriores podamos obtener
\[ X_t=-\sum_{j=1}^\infty\phi^{-j}Z_{t+j}, \qquad t\in\mathbb{Z}, \nonumber \]
como la solución débilmente estacionaria en el caso explosivo.
El resultado del ejemplo anterior conduce a la noción de causalidad lo que significa que el proceso\((X_t: t\in\mathbb{Z})\) tiene una representación en términos del ruido blanco\((Z_s: s\leq t)\) y que, por lo tanto, no está correlacionado con el futuro según lo dado por\((Z_s: s>t)\). Damos la definición para el caso general ARMA.
Definición: Causalidad
Un proceso ARMA (\(p,q\)) dado por (3.1.1) es causal si hay una secuencia\((\psi_j: j\in\mathbb{N}_0)\) tal que\(\sum_{j=0}^\infty|\psi_j|<\infty\) y
\[ X_t=\sum_{j=0}^\infty\psi_jZ_{t-j}, \qquad t\in\mathbb{Z}. \nonumber \]
Causalidad significa que una serie temporal ARMA se puede representar como un proceso lineal. Se vio anteriormente en esta sección cómo un proceso AR (1) cuyo coeficiente satisface la condición\(|\phi|<1\) puede convertirse en un proceso lineal. También se demostró que esto es imposible si\(|\phi|>1\). Las condiciones sobre el parámetro autorregresivo se\(\phi\) pueden replantear en términos del polinomio autorregresivo correspondiente de la\(\phi(z)=1-\phi z\) siguiente manera. Sostiene que
\(|\phi|<1\) if and only if \(\phi(z)\not=0\) for all \(|z|\leq 1, \\[.2cm]\)
\(|\phi|>1\) if and only if \(\phi(z)\not=0\) for all \(|z|\geq 1\).
Resulta que la caracterización en términos de los ceros de los polinomios autorregresivos se traslada del caso AR (1) al caso general ARMA (\(p,q\)). Además, los\(\psi\) pesos del proceso lineal resultante tienen una representación fácil en términos de los polinomios\(\phi(z)\) y\(\theta(z)\). El resultado se resume en el siguiente teorema.
Teorema 3.2.1
\((X_t: t\in\mathbb{Z})\)Sea un proceso ARMA (\(p,q\)) tal que los polinomios\(\phi(z)\) y no\(\theta(z)\) tengan ceros comunes. Entonces\((X_t\colon t\in\mathbb{Z})\) es causal si y sólo si\(\phi(z)\not=0\) para todos\(z\in\mathbb{C}\) con\(|z|\leq 1\). Los coeficientes\((\psi_j: j\in\mathbb{N}_0)\) están determinados por la expansión de la serie de potencia
\[ \psi(z)=\sum_{j=0}^\infty\psi_jz^j=\frac{\theta(z)}{\phi(z)}, \qquad |z|\leq 1. \nonumber \]
Un concepto estrechamente relacionado con la causalidad es la invertibilidad. Esta noción está motivada con el siguiente ejemplo que estudia las propiedades de una serie temporal de promedio móvil de orden 1.
Ejemplo\(\PageIndex{3}\)
Let\((X_t\colon t\in\mathbb{N})\) Ser un proceso MA (1) con parámetro\(\theta=\theta_1\). Es un ejercicio fácil calcular el ACVF y el ACF como
\[ \gamma(h)=\left\{ \begin{array}{l@{\quad}l} (1+\theta^2)\sigma^2, & h=0, \\ \theta\sigma^2, & h=1 \\ 0 & h>1, \end{array}\right. \qquad \rho(h)=\left\{ \begin{array}{l@{\quad}l} 1 & h=0.\\ \displaystyle\theta(1+\theta^2)^{-1}, & h=1. \\ 0 & h>1. \end{array}\right. \nonumber \]
Estos resultados llevan a la conclusión de que\(\rho(h)\) no cambia si\(\theta\) se reemplaza el parámetro por\(\theta^{-1}\). Además, existen pares\((\theta,\sigma^2)\) que conducen al mismo ACVF, por ejemplo\((5,1)\) y\((1/5,25)\). En consecuencia, llegamos al hecho de que los dos modelos MA (1)
\[ X_t=Z_t+\frac 15Z_{t-1},\qquad t\in\mathbb{Z}, \qquad (Z_t\colon t\in\mathbb{Z})\sim\mbox{iid }{\cal N}(0,25), \nonumber \]
y
\[ X_t=\tilde{Z}_t+5\tilde{Z}_{t-1},\qquad t\in\mathbb{Z}, \qquad (\tilde{Z}\colon t\in\mathbb{Z})\sim\mbox{iid }{\cal N}(0,1), \nonumber \]
son indistinguibles porque solo observamos\(X_t\) pero no las variables de ruido\(Z_t\) y\(\tilde{Z}_t\).
Por conveniencia, el estadístico escogerá el modelo que satisfaga el criterio de invertibilidad que se definirá a continuación. Se especifica que la secuencia de ruido se puede representar como un proceso lineal en las observaciones.
Definición: Invertibilidad
Un proceso ARMA (\(p,q\)) dado por (3.1.1) es invertible si hay una secuencia\((\pi_j\colon j\in\mathbb{N}_0)\) tal que\(\sum_{j=0}^\infty|\pi_j|<\infty\) y
\[ Z_t=\sum_{j=0}^\infty\pi_jX_{t-j},\qquad t\in\mathbb{Z}. \nonumber \]
Teorema 3.2.2
\((X_t: t\in\mathbb{Z})\)Sea un proceso ARMA (\(p,q\)) tal que los polinomios\(\phi(z)\) y no\(\theta(z)\) tengan ceros comunes. Entonces\((X_t\colon t\in\mathbb{Z})\) es invertible si y solo si\(\theta(z)\not=0\) para todos\(z \in\mathbb{C}\) con\(|z|\leq 1\). Los coeficientes\((\pi_j)_{j\in\mathbb{N}_0}\) están determinados por la expansión de la serie de potencia
\[ \pi(z)=\sum_{j=0}^\infty\pi_jz^j=\frac{\phi(z)}{\theta(z)}, \qquad |z|\leq 1. \nonumber \]
A partir de ahora se asume que todas las secuencias de ARMA especificadas en la secuela son causales e invertibles a menos que se indique explícitamente lo contrario. El último ejemplo de esta sección destaca la utilidad de la teoría establecida. Se ocupa de la redundancia de parámetros y el cálculo de las secuencias de causalidad e invertibilidad\((\psi_j\colon j\in\mathbb{N}_0)\) and \((\pi_j\colon j\in\mathbb{N}_0)\).
Ejemplo\(\PageIndex{4}\): Parameter redundancy
Considerar las ecuaciones ARMA
\[ X_t=.4X_{t-1}+.21X_{t-2}+Z_t+.6Z_{t-1}+.09Z_{t-2}, \nonumber \]
que parecen generar una secuencia ARMA (2,2). Sin embargo, los polinomios autorregresivos y de promedio móvil tienen un cero común:
\ begin {align*}
\ tilde {\ phi} (z) &=1-.4z-.21z^2 =( 1-.7z) (1+.3z),\\ [.2cm]
\ tilde {\ theta} (z) &=1+.6z+.09z^2 =( 1+.3z) ^2.
\ end {alinear*}
Por lo tanto, se pueden restablecer las ecuaciones ARMA a una secuencia de orden (1,1) y obtener
\[ X_t=.7X_{t-1}+Z_t+.3Z_{t-1}. \nonumber \]
Ahora bien, los polinomios correspondientes no tienen raíces comunes. Tenga en cuenta que las raíces de\(\phi(z)=1-.7z\) y\(\theta(z)=1+.3z\) son\(10/7>1\) y\(-10/3<-1\), respectivamente. Así, los teoremas 3.2.1 y 3.2.2 implican que existen soluciones causales e invertibles. A continuación, los coeficientes correspondientes en las expansiones
\[ X_t=\sum_{j=0}^\infty\psi_jZ_{t-j} \qquad and \qquad Z_t=\sum_{j=0}^\infty\pi_jX_{t-j}, \qquad t\in\mathbb{Z}, \nonumber \]
se calculan. Partiendo de la secuencia de causalidad\((\psi_j: j\in\mathbb{N}_0)\). Redacción, para\(|z|\leq 1\),
\[ \sum_{j=0}^\infty\psi_jz^j =\psi(z) =\frac{\theta(z)}{\phi(z)} =\frac{1+.3z}{1-.7z} =(1+.3z)\sum_{j=0}^\infty(.7z)^j, \nonumber \]
se puede obtener de una comparación de coeficientes que
\[ \psi_0=1 \qquad and \qquad \psi_j=(.7+.3)(.7)^{j-1}=(.7)^{j-1}, \qquad j\in\mathbb{N}. \nonumber \]
Del mismo modo, se computan los coeficientes de invertibilidad\((\pi_j: j\in\mathbb{N}_0)\) a partir de la ecuación
\[ \sum_{j=0}^\infty\pi_jz^j =\pi(z) =\frac{\phi(z)}{\theta(z)} =\frac{1-.7z}{1+.3z} =(1-.7z)\sum_{j=0}^\infty(-.3z)^j \nonumber \]
(\(|z|\leq 1\)) como
\[ \pi_0=1 \qquad and \qquad \pi_j=(-1)^j(.3+.7)(.3)^{j-1}=(-1)^j(.3)^{j-1}. \nonumber \]
En conjunto, los cálculos anteriores ceden a las representaciones explícitas
\[ X_t=Z_t+\sum_{j=1}^\infty(.7)^{j-1}Z_{t-j} \qquad and \qquad Z_t=X_t+\sum_{j=1}^\infty(-1)^j(.3)^{j-1}X_{t-j}. \nonumber \]
En lo que resta de esta sección, se proporciona una manera general para determinar los pesos\((\psi_j\colon j\geq 1)\) para un proceso causal ARMA (\(p,q\)) dado por\(\phi(B)X_t=\theta(B)Z_t\), donde\(\phi(z)\not=0\) para todos\(z\in\mathbb{C}\) tales que\(|z|\leq 1\). Ya que\(\psi(z)=\theta(z)/\phi(z)\) para estos\(z\), el peso se\(\psi_j\) puede calcular haciendo coincidir los coeficientes correspondientes en la ecuación\(\psi(z)\phi(z)=\theta(z)\), es decir,
\[ (\psi_0+\psi_1z+\psi_2z^2+\ldots)(1-\phi_1z-\ldots-\phi_pz^p) = 1+\theta_1z+\ldots+\theta_qz^q. \nonumber \]
Resolver recursivamente para\(\psi_0,\psi_1,\psi_2,\ldots\) da
\ begin {alinear*}
\ psi_0&=1,\
\\ psi_1-\ phi_1\ psi_0&=\ theta_1,\\
\ psi_2-\ phi_1\ psi_1-\ phi_2\ psi_0&=\ theta_2,
\ end {align*}
y así sucesivamente siempre y cuando\(j<\max\{p,q+1\}\). La solución general se puede afirmar como
\[ \psi_j-\sum_{k=1}^j\phi_k\psi_{j-k}=\theta_j, \qquad 0\leq j<\max\{p,q+1\}, \tag{3.2.1}\\[.2cm] \]
\[ \psi_j-\sum_{k=1}^p\phi_k\psi_{j-k}=0, \qquad \phantom{0\leq} j\geq\max\{p,q+1\},\tag{3.2.2} \]
si definimos\(\phi_j=0\) si\(j>p\) y\(\theta_j=0\) si\(j>q\). Por lo tanto, para obtener los coeficientes\(\psi_j\) se tiene que resolver la ecuación de diferencia lineal homogénea (3.2.2) sujeto a las condiciones iniciales especificadas por (3.2.1). Para más información sobre este tema, véanse la Sección 3.6 de Brockwell y Davis (1991) y la Sección 3.3 de Shumway y Stoffer (2006).
Cálculos de R
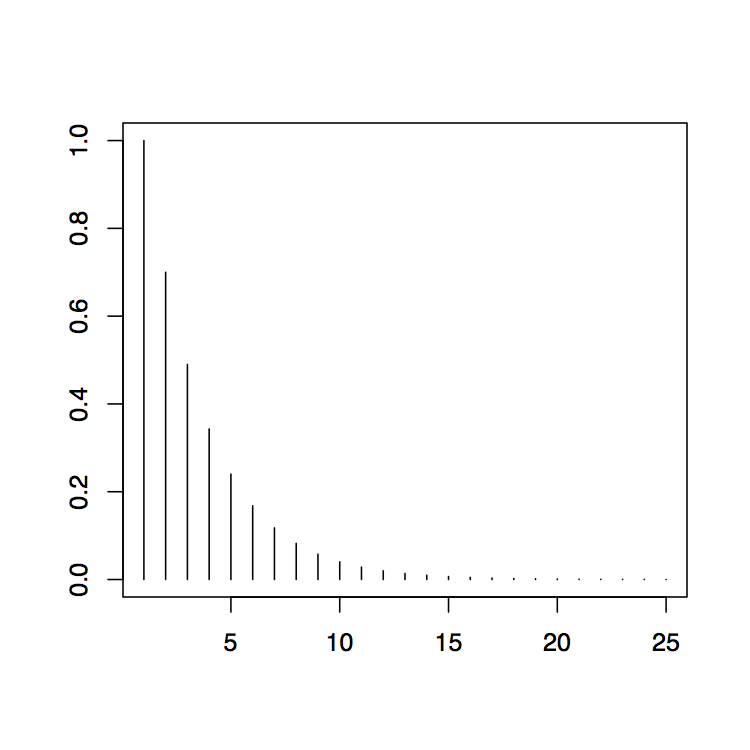
En R, estos cálculos se pueden realizar usando el comando ArmaTomA. Por ejemplo, se pueden usar los comandos
>Armatoma (ar=.7, ma=.3,25)
>parcela (ArmaTomA (ar=.7, ma=.3,25))
lo que producirá la salida mostrada en la Figura 3.4. La gráfica muestra muy bien la decadencia exponencial de los\(\psi\) pesos, que es típica de los procesos ARMA. En la tabla se muestran los pesos en fila\(\psi_0,\ldots,\psi_{24}\). Esto se habilita por la elección de 25 en el argumento de la función ArmaTomA.
| 1.0000000000 | 0.7000000000 | 0.4900000000 | 0.3430000000 | 0.2401000000 |
| 0.1680700000 | 0.1176490000 | 0.0823543000 | 0.0576480100 | 0.0403536070 |
| 0.0282475249 | 0.0197732674 | 0.0138412872 | 0.0096889010 | 0.0067822307 |
| 0.0047475615 | 0.0033232931 | 0.0023263051 | 0.0016284136 | 0.0011398895 |
| 0.0007979227 | 0.0005585459 | 0.0003909821 | 0.0002736875 |
0.0001915812 |