13.4: Dados

Última actualización
Guardar como PDF

Page ID: 152101

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

$\newcommand{\P}{\mathbb{P}}$$\newcommand{\E}{\mathbb{E}}$$\newcommand{\R}{\mathbb{R}}$$\newcommand{\N}{\mathbb{N}}$$\newcommand{\bs}{\boldsymbol}$$\newcommand{\var}{\text{var}}$$\newcommand{\sd}{\text{sd}}$

El juego básico

Craps es un popular juego de casino, por su complejidad y por la rica variedad de apuestas que se pueden hacer.

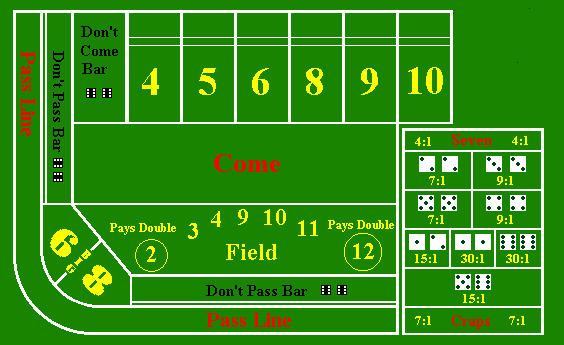
Mesa de Dados — Figura$\PageIndex{1}$: Una típica mesa de dados

Según Richard Epstein, los dados descienden de un juego anterior conocido como Hazard, que data de la Edad Media. Las reglas formales para Hazard fueron establecidas por Montmort a principios de la década de 1700. El origen del nombre dados está envuelto en dudas, pero puede haber venido de los cangrejos ingleses o del francés Crapeaud (para sapo).

Desde un punto de vista matemático, los dados son interesantes porque es un ejemplo de un experimento aleatorio que se lleva a cabo por etapas; la evolución del juego depende críticamente del resultado del primer rollo. En particular, el número de rollos es una variable aleatoria.

Definiciones

Las reglas para los dados son las siguientes:

El jugador (conocido como el tirador) tira un par de dados justos

Si la suma es 7 u 11 en el primer lanzamiento, gana el tirador; este evento se llama natural.
Si la suma es 2, 3 o 12 en el primer lanzamiento, el tirador pierde; este evento se llama dados.
Si la suma es 4, 5, 6, 8, 9 o 10 en el primer lanzamiento, este número se convierte en el punto del tirador. El tirador sigue rodando los dados hasta que o vuelve a rodar el punto (en cuyo caso gana) o tira un 7 (en cuyo caso pierde).

Mientras el tirador gane, o pierda rodando dados, vuelve a entrena los dados y continúa. Una vez que pierde al no hacer su punto, los dados se pasan al siguiente tirador.

Consideremos matemáticamente el juego de dados. Nuestra suposición básica, por supuesto, es que los dados son justos y que los resultados de las distintas tiradas son independientes. Vamos a$N$ denotar el número (aleatorio) de tiradas en el juego y vamos a$(X_i, Y_i)$ denotar el resultado del rollo$i$ th para$i \in \{1, 2, \ldots, N\}$. Por último, vamos$Z_i = X_i + Y_i$, la suma de los puntajes en el rollo$i$ th, y vamos$V$ denotar el evento que gana el tirador.

En el experimento de dados, presiona un solo paso varias veces y observa los resultados. Asegúrate de entender las reglas del juego.

La probabilidad de ganar

Calcularemos la probabilidad de que el tirador gane en etapas, con base en el resultado de la primera tirada.

La suma de las puntuaciones$Z$ en un rollo dado tiene la función de densidad de probabilidad en la siguiente tabla:

$z$	2	3	4	5	6	7	8	9	10	11	12
$\P(Z = z)$	$\frac{1}{36}$	$\frac{2}{36}$	$\frac{3}{36}$	$\frac{4}{36}$	$\frac{5}{36}$	$\frac{6}{36}$	$\frac{5}{36}$	$\frac{4}{36}$	$\frac{3}{36}$	$\frac{2}{36}$	$\frac{1}{36}$

La probabilidad de que el jugador haga su punto se puede calcular usando un simple argumento de condicionamiento. Por ejemplo, supongamos que el jugador lanza 4 inicialmente, de manera que 4 es el punto. El jugador continúa hasta que o lanza 4 de nuevo o lanza 7. Así, la tirada final será un elemento del siguiente conjunto:\[ S_4 = \{(1,3), (2,2), (3,1), (1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\} \] Dado que los dados son justos, estos resultados son igualmente probables, por lo que la probabilidad de que el jugador le haga 4 puntos es$\frac{3}{9}$. Un argumento similar puede ser utilizado para los otros puntos. Aquí están los resultados:

Las probabilidades de hacer el punto$z$ se dan en la siguiente tabla:

$z$	4	5	6	8	9	10
$\P(V \mid Z_1 = z)$	$\frac{3}{9}$	$\frac{4}{10}$	$\frac{5}{11}$	$\frac{5}{11}$	$\frac{4}{10}$	$\frac{3}{9}$

La probabilidad de que gane el tirador es$\P(V) = \frac{244}{495} \approx 0.49293$

Prueba

Esto se desprende de las reglas del juego y del resultado anterior, al condicionar en el primer rollo:

\[ \P(V) = \sum_{z=2}^{12} \P(Z_1 = z) \P(I = 1 \mid Z_1 = z) \]

Tenga en cuenta que los dados son casi un juego limpio. En aras de la integridad, el siguiente resultado da la probabilidad de ganar, dado un punto en la primera tirada.

$ \P(V \mid Z_1 \in \{4, 5, 6, 8, 9, 10\}) = \frac{67}{165} \approx 0.406 $

Prueba

Vamos$ A = \{4, 5, 6, 8, 9, 10\} $. De la definición de probabilidad condicional,\[ \P(V \mid Z_1 \in A) = \frac{\P(V \cap \{Z_1 \in A\})}{\P(Z_1 \in A)} \] Para el numerador, utilizando nuestros resultados anteriores,\[ \P(V \cap \{Z_1 \in A\}) = \sum_{z \in A} \P(V \mid Z_1 = z) \P(Z_1 = z) = \frac{134}{495} \] También de resultados anteriores$ \P(Z_1 \in A) = \frac{2}{3} $.

Apuestas

Hay una desconcertante variedad de apuestas que se pueden hacer en dados. En los ejercicios de esta subsección, discutiremos algunas apuestas típicas y calcularemos la función de densidad de probabilidad, media y desviación estándar de cada una. (La mayoría de estas apuestas se ilustran en la imagen de la tabla de dados de arriba). Sin embargo, tenga en cuenta que algunos de los detalles de las apuestas y, en particular las probabilidades de pago, varían de un casino a otro. Por supuesto, el valor esperado de cualquier apuesta es inevitablemente negativo (para el jugador), y así el jugador está condenado a perder dinero a la larga. No obstante, como veremos, algunas apuestas son mejores que otras.

Pase y no pase

Una apuesta de pase es una apuesta a que el tirador ganará y pagará$1 : 1$.

Dejar$W$ denotar las ganancias de una apuesta de pase unitario. Entonces

$\P(W = -1) = \frac{251}{495}$,$\P(W = 1) = \frac{244}{495}$
$\E(W) = -\frac{7}{495} \approx -0.0141$
$\sd(W) \approx 0.9999$

En el experimento de dados, selecciona la apuesta de pase. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Una apuesta de no pasar es una apuesta que perderá el tirador, excepto que se excluye 12 en el primer tiro (es decir, el tirador pierde, claro, pero el no pase mejor ni gana ni pierde). Este es el significado de la frase no pases barra doble 6 en la mesa de dados. La apuesta de no pasar también paga$1 : 1$.

Dejar$W$ denotar las ganancias para una unidad no pase apuesta. Entonces

$\P(W = -1) = \frac{244}{495}$,$\P(W = 0) = \frac{1}{36}$,$\P(W = 1) = \frac{949}{1980}$
$\E(W) = -\frac{27}{1980} \approx -0.01363$
$\sd(W) \approx 0.9859$

Por lo tanto, la apuesta de no pase es ligeramente mejor para el jugador que la apuesta de pase.

En el experimento de dados, selecciona la apuesta de no pasar. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

La apuesta de venir y la apuesta de no venir son análogas a las apuestas de pase y no pase, respectivamente, excepto que se realizan después de que se haya establecido el punto.

Campo

Una apuesta de campo es una apuesta sobre el resultado del siguiente lanzamiento. Paga$1 : 1$ si se lanza 3, 4, 9, 10 o 11,$2 : 1$ si se lanza 2 o 12, y pierde lo contrario.

Dejar$W$ denotar las ganancias para una apuesta de campo unitario. Entonces

$\P(W = -1) = \frac{5}{9}$,$\P(W = 1) = \frac{7}{18}$,$\P(W = 2) = \frac{1}{18}$
$\E(W) = -\frac{1}{18} \approx -0.0556$
$\sd(W) \approx 1.0787$

En el experimento de dados, selecciona la apuesta de campo. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Siete y Once

Una apuesta de 7 es una apuesta sobre el resultado del siguiente lanzamiento. Paga$4 : 1$ si se lanza un 7. De igual manera, una apuesta de 11 es una apuesta sobre el resultado del siguiente lanzamiento, y paga$15 : 1$ si se lanza un 11. A pesar del romance del número 7, el siguiente ejercicio demuestra que la apuesta 7 es una de las peores apuestas que puedes hacer.

Dejar$W$ denotar las ganancias para una apuesta de unidad 7. Entonces

$\P(W = -1) = \frac{5}{6}$,$\P(W = 4) = \frac{1}{6}$
$\E(W) = -\frac{1}{6} \approx -0.1667$
$\sd(W) \approx 1.8634$

En el experimento de dados, selecciona la apuesta 7. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Dejar$W$ denotar las ganancias para una apuesta de unidad 11. Entonces

$\P(W = -1) = \frac{17}{18}$,$\P(W = 15) = \frac{1}{18}$
$\E(W) = -\frac{1}{9} \approx -0.1111$
$\sd(W) \approx 3.6650$

En el experimento de dados, selecciona la apuesta 11. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Dados

Todas las apuestas de dados son apuestas en el siguiente lanzamiento. La apuesta básica de dados paga$7 : 1$ si se lanza 2, 3 o 12. La apuesta de dados 2 paga$30 : 1$ si se lanza un 2. De igual manera, la apuesta de dados 12 paga$30 : 1$ si se lanza un 12. Por último, la apuesta de dados 3 paga$15 : 1$ si se lanza un 3.

Dejar$W$ denotar las ganancias para una apuesta de dados unitarios. Entonces

$\P(W = -1) = \frac{8}{9}$,$\P(W = 7) = \frac{1}{9}$
$\E(W) = -\frac{1}{9} \approx -0.1111$
$\sd(W) \approx 5.0944$

En el experimento de dados, selecciona la apuesta de dados. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Let$W$ denotar las ganancias para una unidad de dados 2 apuesta o una unidad de dados 12 apuesta. Entonces

$\P(W = -1) = \frac{35}{36}$,$\P(W = 30) = \frac{1}{36}$
$\E(W) = -\frac{5}{36} \approx -0.1389$
$\sd(W) = 5.0944$

En el experimento de dados, selecciona la apuesta de craps 2. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

En el experimento de dados, selecciona la apuesta de los dados 12. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Dejar$W$ denotar las ganancias para una unidad de dados 3 apuesta. Entonces

$\P(W = -1) = \frac{17}{18}$,$ \P(W = 15) = \frac{1}{18} $
$\E(W) = -\frac{1}{9} \approx -0.1111$
$\sd(W) \approx 3.6650$

En el experimento de dados, selecciona la apuesta de craps 3. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Así, de las apuestas de dados, la apuesta básica de dados y la apuesta de craps 3 son las mejores para el jugador, y los dados 2 y los dados 12 son los peores.

Seis Grandes y Ocho Grandes

La apuesta de los 6 grandes es una apuesta que 6 se lanza antes que 7. De igual manera, la apuesta de los 8 grandes es una apuesta que 8 se lanza antes del 7. Ambos pagan incluso dinero$1 : 1$.

Dejar$W$ denotar las ganancias para una apuesta de unidad grande 6 o una apuesta de unidad grande 8. Entonces

$\P(W = -1) = \frac{6}{11}$,$\P(W = 1) = \frac{5}{11}$
$\E(W) = -\frac{1}{11} \approx -0.0909$
$\sd(W) \approx 0.9959$

En el experimento de dados, selecciona la apuesta de los 6 grandes. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

En el experimento de dados, selecciona la apuesta de los 8 grandes. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Apuestas Hardway

Se puede hacer una apuesta dura en cualquiera de los números 4, 6, 8 o 10. Se trata de una apuesta que el número elegido$n$ será lanzado por la vía dura como$ (n/2, n/2) $, antes de que se lance 7 y antes de que se lance el número elegido en cualquier otra combinación. Hardway apuesta por el pago 4 y 10$7 : 1$, mientras que hardway apuesta por el pago de 6 y 8$9 : 1$.

Dejar$W$ denotar las ganancias para una apuesta de unidad hardway 4 o hardway 10. Entonces

$\P(W = -1) = \frac{8}{9}$,$\P(W = 7) = \frac{1}{9}$
$\E(W) = -\frac{1}{9} \approx -0.1111$
$\sd(W) = 2.5142$

En el experimento de dados, selecciona la apuesta hardway 4. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

En el experimento de dados, selecciona la apuesta hardway 10. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Dejar$W$ denotar las ganancias para una apuesta de unidad hardway 6 o hardway 8. Entonces

$\P(W = -1) = \frac{10}{11}$,$\P(W = 9) = \frac{1}{11}$
$\E(W) = -\frac{1}{11} \approx -0.0909$
$\sd(W) \approx 2.8748$

En el experimento de dados, selecciona la apuesta hardway 6. Ejecuta la simulación 1000 veces y compara la densidad empírica y los momentos de$W$ con la densidad y los momentos verdaderos. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

En el experimento de dados, selecciona la apuesta hardway 8. Ejecute la simulación 1000 veces y compare la función de densidad empírica y los momentos de$W$ con la función y momentos de densidad de probabilidad verdadera. Supongamos que apuestes $1 en cada uno de los 1000 juegos. ¿Cuáles serían tus ganancias netas?

Así, las apuestas de hardway 6 y 8 son mejores que las apuestas de hardway 4 y 10 para el jugador, en términos de valor esperado.

La distribución del número de rollos

A continuación vamos a calcular la distribución y los momentos del número de rollos$N$ en un juego de dados. Esta variable aleatoria no es de especial interés para el casino o los jugadores, pero proporciona un buen ejercicio matemáticamente. Por definición, si el tirador gana o pierde en la primera tirada,$N = 1$. De lo contrario, el tirador continúa hasta que ella o hace su punto o rueda 7. En este último caso, podemos utilizar la distribución geométrica sobre la$\N_+$ que gobierna el número de prueba del primer éxito en una secuencia de ensayos de Bernoulli. La distribución de$N$ es una mezcla de distribuciones.

La función de densidad de probabilidad de$N$ es

\[ \P(N = n) = \begin{cases} \frac{12}{36}, & n = 1 \\ \frac{1}{24} \left(\frac{3}{4}\right)^{n-2} + \frac{5}{81} \left(\frac{13}{18}\right)^{n-2} + \frac{55}{648} \left(\frac{25}{36}\right)^{n-2}, & n \in \{2, 3, \ldots\} \end{cases} \]

Prueba

Primero tenga en cuenta que$\P(N = 1 \mid Z_1 = z) = 1$ para$z \in \{2, 3, 7, 11, 12\}$. A continuación,$\P(N = n \mid Z_1 = z) = p_z (1 - p_z)^{n-2}$ para$n \in \{2, 3, \ldots\}$ y para los valores de$z$ y$p_z$ dados en la siguiente tabla:

$z$	4	5	6	8	9	10
$p_z$	$\frac{9}{36}$	$\frac{10}{36}$	$\frac{11}{36}$	$\frac{11}{36}$	$\frac{10}{36}$	$\frac{9}{36}$

Así, la distribución condicional de$N - 1$ dado$Z = z$ es geométrica con probabilidad$p_z$. El resultado final ahora sigue al condicionar en el primer rollo:\[ \P(N = n) = \sum_{z=2}^{12} \P(Z_1 = z) \P(N = n \mid Z_1 = z) \]

Los primeros valores de la función de densidad de probabilidad de$N$ se dan en la siguiente tabla:

$n$	1	2	3	4	5
$\P(N = n)$	0.33333	0.18827	0.13477	0.09657	0.06926

Encuentra la probabilidad de que un juego de dados dure al menos 8 rollos.

Contestar

0.09235

La media y varianza del número de rollos son

$\E(N) = \frac{557}{165} \approx 3.3758$
$\var(N) = \frac{245\,672}{27\,225} \approx 9.02376$

Prueba

Estos resultados también se pueden obtener acondicionando en el primer rollo:\ begin {align}\ E (N) & =\ E\ left [\ E (N\ mid Z_1)\ right] =\ frac {557} {165}\\ E (N^2) & =\ E\ left [\ E\ left [\ E\ left (N^2\ mid Z_1\ right)\ right] =\ frac {61\ ,769} {3025}\ fin {align}

\(z\)	2	3	4	5	6	7	8	9	10	11	12
\(\P(Z = z)\)	\(\frac{1}{36}\)	\(\frac{2}{36}\)	\(\frac{3}{36}\)	\(\frac{4}{36}\)	\(\frac{5}{36}\)	\(\frac{6}{36}\)	\(\frac{5}{36}\)	\(\frac{4}{36}\)	\(\frac{3}{36}\)	\(\frac{2}{36}\)	\(\frac{1}{36}\)

\(z\)	4	5	6	8	9	10
\(\P(V \mid Z_1 = z)\)	\(\frac{3}{9}\)	\(\frac{4}{10}\)	\(\frac{5}{11}\)	\(\frac{5}{11}\)	\(\frac{4}{10}\)	\(\frac{3}{9}\)

\(z\)	4	5	6	8	9	10
\(p_z\)	\(\frac{9}{36}\)	\(\frac{10}{36}\)	\(\frac{11}{36}\)	\(\frac{11}{36}\)	\(\frac{10}{36}\)	\(\frac{9}{36}\)

Search

Text Color

Text Size

Margin Size

Font Type