15.2: Ecuaciones de Renovación
- Page ID
- 152135
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Muchas cantidades de interés en el estudio de los procesos de renovación pueden describirse mediante un tipo especial de ecuación integral conocida como ecuación de renovación. Las ecuaciones de renovación casi siempre surgen condicionando el momento de la primera llegada y utilizando la propiedad definitoria de un proceso de renovación, el hecho de que el proceso se reinicia en cada hora de llegada, independientemente del pasado. Sin embargo, antes de que podamos estudiar las ecuaciones de renovación, necesitamos desarrollar algunos conceptos y herramientas adicionales que involucren medidas, circunvoluciones y transformaciones. Algunos de los resultados en las secciones avanzadas sobre teoría de medidas, funciones generales de distribución, la integral con respecto a una medida, propiedades de la integral y funciones de densidad son necesarios para esta sección. Es posible que deba revisar algunos de estos temas según sea necesario. Como es habitual, asumimos que todas las funciones y conjuntos que se mencionan son medibles con respecto a las\( \sigma \) -álgebras apropiadas. En particular,\( [0, \infty) \) que es nuestro espacio temporal básico, se le da la habitual\( \sigma \) álgebra de Borel generada por los intervalos.
Medidas, Integrales y Transformas
Funciones de distribución y medidas positivas
Recordemos que una función de distribución on\( [0, \infty) \) es una función\( G: [0, \infty) \to [0, \infty) \) que va en aumento y continua desde la derecha. La función de distribución\( G \) define una medida positiva sobre\( [0, \infty) \), que también denotaremos por\( G \), por medio de la fórmula\( G[0, t] = G(t) \) para\( t \in [0, \infty) \).

Esperemos que nuestra notación no cause confusión y quedará claro a partir del contexto si\( G \) se refiere a la medida positiva (una función de conjunto) o a la función de distribución (una función de punto). De manera más general, si\( a, \, b \in [0, \infty) \) y\( a \le b \) entonces\( G(a, b] = G(b) - G(a) \). Tenga en cuenta que la medida positiva asociada a una función de distribución es localmente finita en el sentido de que\( G(A) \lt \infty \)\( A \subset [0, \infty) \) está delimitada. Por supuesto, si no\( A \) tiene límites, bien\( G(A) \) puede ser infinito. La estructura básica de una función de distribución y su medida positiva asociada ocurrieron varias veces en nuestra discusión preliminar de los procesos de renovación:
Distribuciones asociadas a un proceso de renovación.
- La función\( F \) de distribución de los tiempos interllegados define una medida de probabilidad en\( [0, \infty) \)
- El proceso de conteo\( N \) define una medida de conteo (aleatoria) en\( [0, \infty) \)
- la función de renovación\( M \) define una medida positiva (determinista) sobre\( [0, \infty) \)
Supongamos nuevamente que\( G \) es una función de distribución en\( [0, \infty) \). Recordemos que la integral asociada a la medida positiva también\( G \) se llama la integral Lebesgue-Stieltjes asociada a la función de distribución\( G \) (llamada así por Henri Lebesgue y Thomas Stieltjes). Si\( f: [0, \infty) \to \R \) y\( A \subseteq [0, \infty) \) (medible por supuesto), se denota la integral de\( f \) over\( A \) (si existe)\[ \int_A f(t) \, dG(t) \] Utilizamos la más convencional\( \int_0^t f(x) \, dG(x)\) para la integral over\( [0, t] \) y\( \int_0^\infty f(x) \, dG(x) \) para la integral over\( [0, \infty) \). Por otro lado,\( \int_s^t f(x) \, dG(x) \) significa la integral sobre\( (s, t] \) para\( s \lt t \), y\(\int_s^\infty f(x) \, dG(x)\) significa la integral sobre\( (s, \infty) \). Así, la aditividad de lo integral sobre dominios disgregados se mantiene, como debe ser. Por ejemplo, para\( t \in [0, \infty) \),\[ \int_0^\infty f(x) \, dG(x) = \int_0^t f(x) \, dG(x) + \int_t^\infty f(x) \, dG(x) \] Esta notación sería ambigua sin la aclaración, pero es consistente con cómo funciona la medida:\( G[0, t] = G(t) \) para\( t \ge 0 \),\( G(s, t] = G(t) - G(s) \) para\( 0 \le s \lt t \), etc. claro, si\( G \) es continuo como una función, así que eso\( G \) es también continuo como medida, entonces nada de esto importa: la integral en un intervalo es la misma independientemente de que se incluyan o no puntos finales. La siguiente definición es un complemento natural de la propiedad localmente finita de las medidas positivas que estamos considerando.
Una función\( f: [0, \infty) \to \R \) está delimitada localmente si es medible y está delimitada\( [0, t] \) para cada una\( t \in [0, \infty) \).
Las funciones localmente delimitadas forman una clase natural para la cual existen nuestras integrales de interés.
Supongamos que\( G \) es una función de distribución\( [0, \infty) \) activa y\( f: [0, \infty) \to \R \) está delimitada localmente. Entonces\( g: [0, \infty) \to \R \) definido por también\( g(t) = \int_0^t f(s) \, dG(s) \) está delimitado localmente.
Prueba
Supongamos que\( \left|f(s)\right| \le C_t \) para\( s \in [0, t] \) y\( t \in [0, \infty) \). Entonces\[ \int_0^s \left|f(x)\right| \, dG(x) \le C_t G(s) \le C_t G(t), \quad t \in [0, \infty) \] De ahí\( f \) es integrable encendido\( [0, s] \) y la integral está delimitada por\( C_t G(t) \) for\( s \in [0, t] \).
Tenga en cuenta que si\( f \) y\( g \) están acotados localmente, entonces también lo son\( f + g \) y\( f g \). Si\( f \) está aumentando,\( [0, \infty) \) entonces\( f \) está delimitado localmente, por lo que en particular, una función de distribución en\( [0, \infty) \) está delimitada localmente. Si\( f \) es continuo\( [0, \infty) \), entonces\( f \) está delimitado localmente. Del mismo modo, si\( G \) y\( H \) son funciones de distribución\( [0, \infty) \) encendidas y si\( c \in (0, \infty) \), entonces\( G + H \) y también\( c G \) son funciones de distribución encendidas\( [0, \infty) \). La convolución, que consideramos a continuación, es otra forma de construir nuevas distribuciones a\( [0, \infty) \) partir de las que ya tenemos.
Convolución
El término convolución significa cosas diferentes en diferentes escenarios. Empecemos por la definición que conocemos, la convolución de las funciones de densidad de probabilidad, en nuestro espacio de interés\( [0, \infty) \).
Supongamos que\( X \) y\( Y \) son variables aleatorias independientes con valores en\( [0, \infty) \) y con funciones de densidad de probabilidad\( f \) y\( g \), respectivamente. Entonces\( X + Y \) tiene la función de densidad de probabilidad\( f * g \) dada de la siguiente manera, en los casos discretos y continuos, respectivamente\ begin {align} (f * g) (t) & =\ sum_ {s\ in [0, t]} f (t - s) g (s)\\ (f * g) (t) & =\ int_0^t f (t - s) g (s)\, ds\ end {align}
En el caso discreto, se entiende que\( t \) es un valor posible de\( X + Y \), y la suma está sobre la colección contable de\( s \in [0, t] \) con\( s \) un valor de\( X \) y\( t - s \) un valor de\( Y \). A menudo en este caso, las variables aleatorias toman valores\( \N \), en cuyo caso la suma es simplemente sobre el conjunto\( \{0, 1, \ldots, t\} \) para\( t \in \N \). Los casos discretos y continuos podrían unificarse definiendo convolución con respecto a una medida positiva general sobre\( [0, \infty) \). Además, la definición claramente tiene sentido para funciones que no son necesariamente funciones de densidad de probabilidad.
Supongamos que\( f, \, g: [0, \infty) \to \R \) ae acotado localmente y que\( H \) es una función de distribución en\( [0, \infty) \). La convolución de\( f \) y\( g \) con respecto a\( H \) es la función en\( [0, \infty) \) definida por\[ t \mapsto \int_0^t f(t - s) g(s) \, dH(s) \]
Si\( f \) y\( g \) son funciones de densidad de probabilidad para distribuciones discretas en un conjunto contable\( C \subseteq [0, \infty) \) y si\( H \) está contando la medida en\( C \), obtenemos convolución discreta, como arriba. Si\( f \) y\( g \) son funciones de densidad de probabilidad para distribuciones continuas en\( [0, \infty) \) y si\( H \) es medida de Lebesgue, obtenemos convolución continua, como arriba. Tenga en cuenta sin embargo, que si no\( g \) es negativo entonces\( G(t) = \int_0^t g(s) \, dH(s) \) para\( t \in [0, \infty) \) define otra función de distribución en\( [0, \infty) \), y la integral de convolución anterior es simplemente\( \int_0^t f(t - s) \, dG(s) \). Esto motiva nuestra próxima versión de convolución, la que usaremos en el resto de esta sección.
Supongamos que\( f: [0, \infty) \to \R \) está acotado localmente y que\( G \) es una función de distribución en\( [0, \infty) \). La convolución de la función\( f \) con la distribución\( G \) es la función\( f * G \) definida por\[ (f * G)(t) = \int_0^t f(t - s) \, dG(s), \quad t \in [0, \infty) \]
Tenga en cuenta que si\( F \) y\( G \) son funciones de distribución\( [0, \infty) \) encendidas, la convolución tiene\( F * G \) sentido, con\( F \) simplemente como una función y\( G \) como una función de distribución. El resultado es otra función de distribución. Además en este caso, la operación es conmutativa.
Si\( F \) y\( G \) son funciones de distribución\( [0, \infty) \), entonces también\( F * G \) es una función de distribución en\( [0, \infty) \), y\( F * G = G * F \)
Prueba
Dejar\( F \otimes G \) y\( G \otimes F \) denotar las medidas habituales del producto en\([0, \infty)^2 = [0, \infty) \times [0, \infty)\). Para\( t \in [0, \infty) \), let\( T_t = \left\{(r, s) \in [0, \infty)^2: r + s \le t\right\} \), la región triangular con vértices\( (0, 0) \),\( (t, 0) \), y\( (0, t) \). Entonces\[ (F * G)(t) = \int_0^t F(t - s) \, dG(s) = \int_0^t \int_0^{t - s} dF(r) \, dG(s) = (F \otimes G)\left(T_t\right) \] Esto define claramente una función de distribución. Específicamente, si\( 0 \le s \le t \lt \infty \) entonces\( T_s \subseteq T_t \) es así\((F * G)(s) = (F \otimes G)(T_s) \le (F \otimes G)(T_t) = (F * G)(t)\). De ahí\( F * G \) que esté disminuyendo. Si\( t \in [0, \infty) \) y\( t_n \in [0, \infty) \) para\( n \in \N_+ \) con\( t_n \downarrow t \) como\( n \to \infty \) entonces\( T_{t_n} \downarrow T_t \) (en el sentido de subconjunto) como\( n \to \infty \) así por la propiedad de continuidad de\( F \otimes G \) tenemos\( (F * G)(t_n) = (F \otimes G)\left(T_{t_n}\right) \downarrow (F \otimes G)(T_t) = (F * G)(t) \) como\( n \to \infty \). De ahí\( F * G \) que sea continuo desde la derecha.
Para la propiedad conmutativa, tenemos\((F * G)(t) = (F \otimes G)(T_t)\) y\( (G * F)(t) = (G \otimes F)(T_t) \). Por la simetría del triángulo\( T_t \) con respecto a la diagonal\( \{(s, s): s \in [0, \infty)\} \), estas son las mismas.
Si\( F \) y\( G \) son funciones de distribución de probabilidad correspondientes a variables aleatorias independientes\( X \) y\( Y \) con valores en\( [0, \infty) \), entonces\( F * G \) es la función de distribución probabiltiy de\( X + Y \). Supongamos ahora que\( f: [0, \infty) \to \R \) está acotado localmente y que\( G \) y\( H \) son funciones de distribución encendidas\( [0, \infty) \). Del resultado anterior, ambos\( (f * G) * H \) y tienen\( f * (G * H) \) sentido. Afortunadamente, son lo mismo por lo que la convolución es asociativa.
Supongamos que\( f: [0, \infty) \to \R \) está acotado localmente y que\( G \) y\( H \) son funciones de distribución encendidas\( [0, \infty) \). Entonces\[ (f * G) * H = f * (G * H) \]
Prueba
Para\( t \in [0, \infty) \),\[ [(f * G) * H](t) = \int_0^t (f * G)(t - s) \, dH(s) = \int_0^t \int_0^{t - s} f(t - s - r) \, dG(r) \, dH(s) = [f * (G * H)](t) \]
Finalmente, la convolución es una operación lineal. Es decir, la convolución conserva sumas y múltiplos escalares, siempre que estos tengan sentido.
Supongamos que\( f, \, g: [0, \infty) \to \R \) están delimitados localmente,\( H \) es una función de distribución en\( [0, \infty) \), y\( c \in \R \). Entonces
- \( (f + g) * H = (f * H) + (g * H) \)
- \( (c f) * H = c (f * H) \)
Prueba
Estas propiedades siguen fácilmente de las propiedades de linealidad de la integral.
- \( [(f + g) * H](t) = \int_0^t (f + g)(t - s) \, dH(s) = \int_0^t f(t - s) \, dH(s) + \int_0^t g(t - s) \, dH(s) = (f * H)(t) + (g * H)(t) \)
- \( [(c f) * H](t) = \int_0^t c f(t - s) \, dH(s) = c \int_0^t f(t - s) \, dH(s) = c (f * H)(t) \)
Supongamos que\( f: [0, \infty) \to \R \) está delimitado localmente,\( G \) y\( H \) son funciones de distribución en\( [0, \infty) \), y eso\( c \in (0, \infty) \). Entonces
- \( f * (G + H) = (f * G) + (f * H) \)
- \( f * (c G) = c (f * G) \)
Prueba
Estas propiedades también se derivan de las propiedades de linealidad de la integral.
- \( [f * (G + H)](t) = \int_0^t f(t - s) \, d(G + H)(s) = \int_0^t f(t - s) \, dG(s) + \int_0^t f(t - s) \, dH(s) = (f * G)(t) + (f * H)(t) \)
- \( [f * (c G)](t) = \int_0^t f(t - s) \, d(c G)(s) = c \int_0^t f(t - s) \, dG(s) = c (f * G)(t) \)
Laplace Transforma
Al igual que la convolución, el término transformación de Laplace (llamado así por Pierre Simon Laplace, por supuesto) puede significar cosas ligeramente diferentes en diferentes escenarios. Comenzamos con la definición habitual que hayas visto en tu estudio de ecuaciones diferenciales u otras materias:
La transformada de Laplace de una función\( f: [0, \infty) \to \R \) es la función\( \phi \) definida de la siguiente manera,\( s \in (0, \infty) \) para todos los cuales existe la integral en\( \R \):\[ \phi(s) = \int_0^\infty e^{-s t} f(t) \, dt \]
Supongamos que eso no\( f \) es negativo, para que la integral que define la transformación exista en\( [0, \infty] \) para cada uno\( s \in (0, \infty) \). Si\( \phi(s_0) \lt \infty \) para algunos\( s_0 \in (0, \infty) \) entonces\( \phi(s) \lt \infty\) para\( s \ge s_0 \). La transformación de una función general\( f \) existe (in\( \R \)) si y solo si la transformación de\( \left|f\right| \) es finita at\( s \). De ello se deduce que si\( f \) tiene una transformada de Laplace, entonces la transformada\( \phi \) se define en un intervalo de la forma\( (a, \infty) \) para algunos\( a \in (0, \infty) \). El dominio real es de muy poca importancia; el punto principal es que la transformación de Laplace, si existe, se definirá para todos suficientemente grandes\( s \). Básicamente, una función no negativa no logrará tener una transformación de Laplace si crece a un ritmo hiperexponencial
como\( t \to \infty \).
Podríamos generalizar la transformación de Laplace reemplazando la integral de Riemann o Lebesgue por la integral sobre una medida positiva en\( [0, \infty) \).
Supongamos que eso\( G \) es una distribución en\( [0, \infty) \). La transformación de Laplace de\( f: [0, \infty) \to \R \) con respecto a\( G \) es la función que se da a continuación, definida para todos\( s \in (0, \infty) \) para los cuales existe la integral en\( \R \):\[ s \mapsto \int_0^\infty e^{-s t} f(t) \, dG(t) \]
Sin embargo, como antes, si no\( f \) es negativo, entonces\( H(t) = \int_0^t f(x) \, dG(x) \) for\( t \in [0, \infty) \) define otra función de distribución, y la integral anterior es simplemente\( \int_0^\infty e^{-s t} \, dH(t) \). Esto motiva el definiton para la transformación de Laplace de una distribución.
La transformada de Laplace de una distribución\( F \) on\( [0, \infty) \) es la función\( \Phi \) definida de la siguiente manera,\( s \in (0, \infty) \) para todos los cuales la integral es finita:\[\Phi(s) = \int_0^\infty e^{-s t} dF(t) \]
Una vez más si\( F \) tiene una transformación de Laplace, entonces la transformación se definirá para todos suficientemente grandes\( s \in (0, \infty) \). Intentaremos ser explícitos al explicar cuál de las definiciones de transformación de Laplace se está utilizando. Para una función genérica, se aplica la primera definición, y usaremos una letra griega minúscula. Si la función es una función de distribución, cualquiera de las definiciones tiene sentido, pero suele ser esta última la que es apropiada, en cuyo caso usamos una letra griega mayúscula. Afortunadamente, existe una relación sencilla entre ambos.
Supongamos que\( F \) es una función de distribución en\( [0, \infty) \). Dejar\( \Phi \) denotar la transformación de Laplace de la distribución\( F \) y\( \phi \) la transformación de Laplace de la función\( F \). Entonces\( \Phi(s) = s \phi(s) \).
Prueba
La herramienta principal es el teorema de Fubini (llamado así por Guido Fubini), que nos permite intercambiar el orden de integración por una función no negativa. \ begin {align}\ phi (s) & =\ int_0^\ infty e^ {-s t} F (t)\, dt =\ int_0^\ infty e^ {-s t}\ izquierda (\ int_0^t dF (x)\ derecha) dt\\ & =\ int_0^\ infty\ izquierda (\ int_x^\ infty e^ {-s t} dt\ derecha) dF (x) =\ int_0^\ infty\ frac {1} {s} e^ {-s x} dF (x) =\ frac {1} {s}\ Phi (s)\ end {align}
Para una distribución de probabilidad, también existe una relación simple entre la transformada de Laplace y la función generadora de momentos.
Supongamos que\( X \) es una variable aleatoria con valores en\( [0, \infty) \) y con función de distribución de probabilidad\( F \). La transformación de Laplace\( \Phi \) y la función generadora de momento\( \Gamma \) de la distribución\( F \) se dan de la siguiente manera, y así\( \Phi(s) = \Gamma(-s) \) para todos\( s \in (0, \infty) \). \ begin {align}\ phi (s) & =\ E\ izquierda (e^ {-s X}\ derecha) =\ int_0^\ infty e^ {-s t} dF (t)\\ gamma (s) & =\ E\ izquierda (e^ {s X}\ derecha) =\ int_0^\ infty e^ {s t} dF (t)\ end {align}
En particular, una distribución de probabilidad\( F \) en\( [0, \infty) \) siempre tiene una transformada de Laplace\( \Phi \), definida en\( (0, \infty) \). Tenga en cuenta también que si\( F(0) \lt 1 \) (así que eso no\( X \) es deterministicamente 0), entonces\( \Phi(s) \lt 1 \) para\( s \in (0, \infty) \).
Las transformaciones de Laplace son importantes para las distribuciones generales por las mismas razones que las funciones generadoras de momento son importantes para las distribuciones de probabilidad: la transformación de una distribución determina de manera única la distribución, y la transformación de una convolución es el producto de la correspondiente\( [0, \infty) \) transforma (y los productos son matemáticamente mucho más agradables que las circunvoluciones). Los siguientes teoremas dan las propiedades esenciales de las transformaciones de Laplace. Suponemos que las transformaciones existen, por supuesto, y debe entenderse que las ecuaciones que involucran transformaciones se mantienen suficientemente grandes\( s \in (0, \infty) \).
Supongamos que\( F \) y\( G \) son distribuciones\( [0, \infty) \) con las transformaciones de Laplace\( \Phi \) y\( \Gamma \), respectivamente. Si\( \Phi(s) = \Gamma(s) \) por\( s \) lo suficientemente grande, entonces\( G = H \)
En el caso de las funciones generales on\( [0, \infty) \), la conclusión es que\( f = g \) excepto quizás en un subconjunto\( [0, \infty) \) de la medida 0. La transformación de Laplace es una operación lineal.
Supongamos que\( f, \, g : [0, \infty) \to \R \) tienen Laplace transforma\( \phi \) y\( \gamma \), respectivamente, y\( c \in \R\) luego
- \( f + g \)ha transformado Laplace\( \phi + \gamma \)
- \(c f \)ha transformado Laplace\( c \phi \)
Prueba
Estas propiedades se derivan de la linealidad de la integral. Para\( s \) suficientemente grandes,
- \( \int_0^\infty e^{- s t} [f(t) + g(t)] \, dt = \int_0^\infty e^{-s t} f(t) \, dt + \int_0^\infty e^{-s t} g(t) \, dt = \phi(s) + \gamma(s) \)
- \( \int_0^\infty e^{-s t} c f(t) \, dt = c \int_0^\infty e^{-s t} f(t) \, dt = c \phi(s) \)
Las mismas propiedades se mantienen para distribuciones on\( [0, \infty) \) with\( c \in (0, \infty) \). Las transformaciones integrales tienen un efecto suavizante. Las transformaciones de Laplace son diferenciables, y podemos intercambiar los operadores derivados e integrales.
Supongamos que\( f: [0, \infty) \to \R \) tiene Lapalce transformar\( \phi \). Entonces\( \phi \) tiene derivados de todos los órdenes y\[ \phi^{(n)}(s) = \int_0^\infty (-1)^n t^n e^{- s t} f(t) \, dt \]
Reafirmada,\( (-1)^n \phi^{(n)} \) es la transformación de Laplace de la función\( t \mapsto t^n f(t) \). Nuevamente, una de las propiedades más importantes es que la transformación de Laplace convierte la convolución en productos.
Supongamos que\( f: [0, \infty) \to \R \) está delimitado localmente con la transformación de Laplace\( \phi \), y que\( G \) es una función de distribución\( [0, \infty) \) con la transformación de Laplace\( \Gamma \). Entonces Laplace\(f * G\) se ha transformado\( \phi \cdot \Gamma \).
Prueba
Por definición, la transformación de Laplace de\( f * G \) es\[ \int_0^\infty e^{-s t} (f * G)(t) \, dt = \int_0^\infty e^{-s t} \left(\int_0^t f(t - x) \, dG(x)\right) dt \] Escribir\( e^{-s t} = e^{-s(t - x)} e^{-s x} \) e invertir el orden de integración, la última integral iterada puede escribirse como\[ \int_0^\infty e^{-s x} \left(\int_x^\infty e^{-s (t - x)} f(t - x) \, dt\right) dG(x) \] El intercambio se justifica, una vez más, por el teorema de Fubini, ya que nuestras funciones son integrables (para suficientemente grandes \( s \in (0, \infty) \)). Finalmente con la sustitución\( y = t - x \) la última integral iterada se puede escribir como un producto\[ \left(\int_0^\infty e^{-s y} f(y) \, dy\right) \left(\int_0^\infty e^-{s x} dG(x)\right) = \phi(s) \Gamma(s) \]Si\( F \) y\( G \) están las distribuciones encendidas\( [0, \infty) \), entonces también lo es\( F * G \). El resultado anterior aplica, por supuesto, con\( F \) y\( F * G \) pensado como funciones y\( G \) como una distribución, pero multiplicando por\( s \) y usando el teorema anterior, es claro que el resultado también es cierto con los tres como distribuciones.
Ecuaciones de Renovación y sus Soluciones
Armados con nuestra nueva maquinaria analítica, podemos volver al estudio de los procesos de renovación. Así, supongamos que tenemos un proceso de renovación con secuencia interllegada\( \bs{X} = (X_1, X_2, \ldots) \), secuencia de tiempo de llegada y proceso de conteo\( \bs{N} = \{N_t: t \in [0, \infty)\} \).\( \bs{T} = (T_0, T_1, \ldots) \) Como es habitual, vamos a\( F \) denotar la función común de distribución de los tiempos interllegados, y dejar\( M \) denotar la función de renovación, de modo que\( M(t) = \E(N_t) \) para\( t \in [0, \infty) \). Por supuesto, la función de distribución de probabilidad\( F \) define una medida de probabilidad en\( [0, \infty) \), pero como se señaló anteriormente, también\( M \) es una función de distribución y así define una medida positiva en\( [0, \infty) \). Recordemos que\( F^c = 1 - F \) es la función de distribución correcta (o función de confiabilidad) de un tiempo entre llegadas.
Las distribuciones de los tiempos de llegada son los poderes de convolución de\( F \). Es decir,\( F_n = F^{*n} = F * F * \cdots * F \).
Prueba
Esto se desprende de las definiciones:\( F_n \) es la función de distribución de\( T_n \), y\( T_n = \sum_{i=1}^n X_i \). Dado que\( \bs{X} \) es una secuencia independiente, distribuida idénticamente,\( F_n = F^{*n} \)
La siguiente definición es la central para esta sección.
Supongamos que\( a: [0, \infty) \to \R \) está acotado localmente. Una ecuación integral de la forma\[ u = a + u * F \] para una función desconocida\( u: [0, \infty) \to \R \) se llama ecuación de renovación para\( u \).
A menudo\( u(t) = \E(U_t) \) donde\( \left\{U_t: t \in [0, \infty)\right\} \) hay un proceso aleatorio de interés asociado con el proceso de renovación. La ecuación de renovación proviene de condicionar la primera hora de llegada\( T_1 = X_1 \), y luego usar la propiedad definitoria del proceso de renovación, el hecho de que el proceso comienza de nuevo, de manera interdependiente del pasado, a la hora de llegada. Nuestro siguiente resultado importante ilustra esto.
Ecuaciones de renovación para\( M \) y\( F \):
- \( M = F + M * F \)
- \( F = M - F * M \)
Prueba
- Condicionamos el tiempo de la primera llegada\( X_1 \) y rompemos el dominio de la\( [0, \infty) \) integración en las dos partes\( [0, t] \) y\( (t, \infty) \):\[ M(t) = \E(N_t) = \int_0^\infty E(N_t \mid X_1 = s) \, dF(s) = \int_0^t \E(N_t \mid X_1 = s) \, dF(s) + \int_t^\infty \E(N_t \mid X_1 = s) \, dF(s) \] Si\( s \gt t \) entonces\( \E(N_t \mid X_1 = s) = 0 \). Si\( 0 \le s \le t \), entonces por la renovación de la propiedad,\( \E(N_t \mid X_1 = s) = 1 + M(t - s) \). De ahí que tengamos\[ M(t) = \int_0^t [1 + M(t - s)] \, dF(s) = F(t) + (M * F)(t) \]
- De (a) y la propiedad conmutativa de convolución dada anteriormente (recordemos que también\( M \) es una función de distribución), tenemos\( F = M - M * F = M - F * M \)
Así, la propia función de renovación satisface una ecuación de renovación. Por supuesto, ya tenemos una fórmula
para\( M \), a saber\( M = \sum_{n=1}^\infty F_n \). Sin embargo, a veces se\( M \) puede calcular más fácilmente a partir de la ecuación de renovación directamente. El siguiente resultado es la versión transform del resultado anterior:
Las distribuciones\( F \) y\( M \) tienen transfroms Laplace\( \Phi \) y\( \Gamma \), respectivamente, que se relacionan de la siguiente manera:\[ \Gamma = \frac{\Phi}{1 - \Phi}, \quad \Phi = \frac{\Gamma}{\Gamma + 1} \]
Prueba de la ecuación de renovación
Tomando Laplace se transforma a través de la ecuación de renovación\( M = F + M * F \) (y tratando todos los términos como distribuciones), tenemos\( \Gamma = \Phi + \Gamma \Phi \). Resolviendo para\( \Gamma \) da el resultado. Recordemos que ya que\( F \) es una distribución de probabilidad en\( [0, \infty) \) con\( F(0) \lt 1 \), lo sabemos\( 0 \lt \Phi(s) \lt 1 \) para\( s \in (0, \infty) \). La segunda ecuación se desprende de la primera por álgebra simple.
Prueba de convolución
Recordemos eso\( M = \sum_{n=1}^\infty F^{* n} \). Tomando trasformas de Laplace (nuevamente tratando todos los términos como distribuciones), y usando series geométricas tenemos\[ \Gamma = \sum_{n=1}^\infty \Phi^n = \frac{\Phi}{1 - \Phi} \] Recordemos nuevamente eso\( 0 \lt \Phi(s) \lt 1 \) para\( s \in (0, \infty) \). Una vez más, la segunda ecuación se desprende de la primera por álgebra simple.
En particular, la distribución de renovación\( M \) siempre tiene una transformación de Laplace. El siguiente teorema da los resultados fundamentales sobre la solución de la ecuación de renovación.
Supongamos que\( a: [0, \infty) \to \R \) está acotado localmente. Entonces es la única solución limitada localmente a la ecuación\( u = a + u * F \) de renovación\( u = a + a * M \).
Prueba directa
Supongamos que\( u = a + a * M \). Entonces\( u * F = a * F + a * M * F\). Pero a partir de la ecuación de renovación para\( M \) arriba,\( M * F = M - F \). De ahí que tengamos\(u * F = a * F + a * (M - F) = a * [F + (M - F)] = a * M \). Pero\( a * M = u - a \) por definición de\( u \), así\( u = a + u * F \) y por lo tanto\( u \) es una solución a la ecuación de renovación. Siguiente ya que\( a \) está acotada localmente, así es\( u = a + a * M \). Supongamos ahora que\( v \) es otra solución localmente delimitada de la ecuación integral, y vamos\( w = u - v \). Entonces\( w \) se delimita localmente y\( w * F = (u * F) - (v * F) = [(u - a) - (v - a) = u - v = w \). De ahí\( w = w * F_n \) para\( n \in \N_+ \). Supongamos que\( \left|w(s)\right| \le D_t \) para\( 0 \le s \le t \). Entonces\( \left|w(t)\right| \le D_t \, F_n(t) \) para\( n \in \N_+ \). Ya que\( M(t) = \sum_{n=1}^\infty F_n(t) \lt \infty \) se deduce que\( F_n(t) \to 0 \) como\( n \to \infty \). De ahí\( w(t) = 0 \) para\( t \in [0, \infty) \) y así\( u = v \).
Prueba de las transformaciones de Laplace
Dejar\( \alpha \) y\( \theta \) denotar las transformaciones de Laplace de las funciones\( a \) y\( u \), respectivamente, y\( \Phi \) la transformación de Laplace de la distribución\( F \). Tomando Laplace se transforma a través de las ecuaciones de renovación da la ecuación algebraica simple\( \theta = \alpha + \theta \Phi \). Resolviendo dar\[ \theta = \frac{\alpha}{1 - \Phi} = \alpha \left(1 + \frac{\Phi}{1 - \Phi}\right) = \alpha + \alpha \Gamma \] dónde\( \Gamma = \frac{\Phi}{1 - \Phi} \) está la transformación de Laplace de la distribución\( M \). Así\( \theta \) es la transformación de\( a + a * M \).
Volviendo a las ecuaciones de renovación para\( M \) y por\( F \) encima, ahora vemos que la función de renovación determina\( M \) completamente el proceso de renovación: a partir de lo\( M \) que podemos obtener\( F \), y todo se construye en última instancia a partir de los tiempos de interllegada. Por supuesto, esto también queda claro a partir del resultado de la transformada de Laplace anterior que da ecuaciones algebraicas simples para cada transformada en términos de la otra.
La distribución de las variables de edad
Recordemos la definición de las variables de edad. Un tiempo determinista\( t \in [0, \infty) \) cae en el intervalo de renovación aleatoria\(\left[T_{N_t}, T_{N_t + 1}\right)\). La vida actual (o edad) en el momento\( t \) es\( C_t = t - T_{N_t} \), la vida restante en el tiempo lo\( t \) es\( R_t = T_{N_t + 1} - t \), y la vida total en el momento\( t \) lo es\( L_t = T_{N_t + 1} - T_{N_t} \). En la configuración de confiabilidad habitual,\( C_t \) se encuentra la antigüedad del dispositivo que está en servicio en el momento\( t \), mientras que\( R_t \) es el tiempo hasta que ese dispositivo falla, y\( L_t \) es la vida útil total del dispositivo.
Para\( t, \, y \in [0, \infty) \), vamos\[ r_y(t) = \P(R_t \gt y) = \P\left(N(t, t + y] = 0\right) \] y vamos\( F^c_y(t) = F^c(t + y) \). Tenga en cuenta que\( y \mapsto r_y(t)\) es la función de distribución correcta de\( R_t \). Derivaremos y luego resolveremos una ecuación de renovación para\( r_y \) condicionando el momento de la primera llegada. Luego podemos encontrar ecuaciones integrales que describen la distribución de la edad actual y la distribución conjunta de las edades actuales y restantes.
Para\( y \in [0, \infty) \),\( r_y \) satisface la ecuación de renovación\( r_y = F^c_y + r_y * F \) y por lo tanto para\( t \in [0, \infty) \),\[ \P(R_t \gt y) = F^c(t + y) + \int_0^t F^c(t + y - s) \, dM(s), \quad y \ge 0 \]
Prueba
Como es habitual, condicionamos el momento de la primera renovación: Naturalmente,\[ \P(R_t \gt y) = \int_0^\infty \P(R_t \gt y \mid X_1 = s) \, dF(s) \] nos llevan a romper el dominio\( [0, \infty) \) de la integral en tres partes\( [0, t] \)\( (t, t + y] \),, y\( (t + y, \infty) \), que tomamos una a la vez.
Tenga en cuenta primero que\( \P(R_t \gt y \mid X_1 = s) = \P(R_{t-s} \gt y) \) para\( s \in [0, t] \)

Siguiente nota que\( \P(R_t \gt y \mid X_1 = s) = 0 \) para\( s \in (t, t + y] \)

Por último señalar que\( \P(R_t \gt y \mid X_1 = s) = 1 \) para\( s \in (t + y, \infty) \)

Armando las piezas que tenemos\[ \P(R_t \gt y) = \int_0^t \P(R_{t - s} \gt y) \, dF(s) + \int_t^{t+y} 0 \, dF(s) + \int_{t + y}^\infty 1 \, dF(s) \] En cuanto a nuestra notación de función, la primera integral es\( (r_y * F)(t) \), la segunda integral es 0 por supuesto, y la tercera integral lo es\( 1 - F(t + y) = F_y^c(t) \). Así se satisface la ecuación de renovación y la fórmula para\( \P(R_t \gt y) \) sigue el teorema fundamental sobre las ecuaciones de renovación.
Ahora podemos describir la distribución de la edad actual.
Para\( t \in [0, \infty) \),\[ \P(C_t \ge x) = F^c(t) + \int_0^{t-x} F^c(t - s) \, dM(s), \quad x \in [0, t] \]
Prueba
Esto se desprende del teorema anterior y el hecho de que\( \P(C_t \ge x) = \P(R_{t-x} \gt x) \) para\( x \in [0, t] \).
Finalmente obtenemos la distribución conjunta de las edades actuales y restantes.
Para\( t \in [0, \infty) \),\[ \P(C_t \ge x, R_t \gt y) = F^c(t + y) + \int_0^{t-x} F^c(t + y - s) \, dM(s), \quad x \in [0, t], \; y \in [0, \infty) \]
Prueba
Recordemos eso\( \P(C_t \ge x, R_t \gt y) = \P(R_{t-x} \gt x + y) \). El resultado ahora se desprende del resultado anterior para la vida restante.
Ejemplos y Casos Especiales
Interllegadas distribuidas uniformemente
Considera el proceso de renovación con tiempos interllegados distribuidos uniformemente en\( [0, 1] \). Por lo tanto, la función de distribución de un tiempo interllegada es\( F(x) = x \) para\( 0 \le x \le 1 \). La función de renovación se\( M \) puede calcular a partir de la ecuación de renovación general para\( M \) resolviendo sucesivamente ecuaciones diferenciales. En el siguiente ejercicio se dan los dos primeros casos.
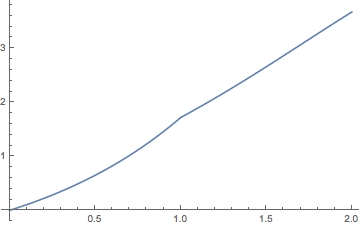
En el intervalo\( [0, 2] \), muestra que\( M \) se da de la siguiente manera:
- \( M(t) = e^t - 1 \)para\( 0 \le t \le 1 \)
- \( M(t) = (e^t - 1) - (t - 1)e^{t-1} \)para\( 1 \le t \le 2 \)
Solución
Demostrar que la transformación\(\Phi\) de Laplace de la distribución entre llegadas\( F \) y la transformación\( \Gamma \) de Laplace de la distribución de renovación\( M \) son dadas por\[ \Phi(s) = \frac{1 - e^{-s}}{s}, \; \Gamma(s) = \frac{1 - e^{-s}}{s - 1 + e^{-s}}; \quad s \in (0, \infty) \]
Solución
Primero tenga en cuenta que\[\Phi(s) = \int_0^\infty e^{-s t} dF(t) = \int_0^1 e^{-s t} dt = \frac{1 - e^{-s}}{s}, \quad s \in (0, \infty)\] La fórmula para\( \Gamma \) se desprende de\( \Gamma = \Phi \big/ (1 - \Phi) \).
Abra el experimento de renovación y seleccione la distribución uniforme entre llegadas en el intervalo\( [0, 1] \). Para cada uno de los siguientes valores del parámetro de tiempo, ejecute el experimento 1000 veces y anote la forma y ubicación de la distribución empírica de la variable de conteo.
- \( t = 5 \)
- \( t = 10 \)
- \( t = 15 \)
- \( t = 20 \)
- \( t = 25 \)
- \( t = 30 \)
El proceso de Poisson
Recordemos que el proceso de Poisson tiene tiempos interllegados que se distribuyen exponencialmente con el parámetro rate\( r \gt 0 \). Así, la función de distribución entre llegadas\( F \) viene dada por\( F(x) = 1 - e^{-r x} \) for\( x \in [0, \infty) \). Los siguientes ejercicios dan pruebas alternas de los resultados fundamentales obtenidos en la Introducción.
Demostrar que la función de renovación\( M \) viene dada por\( M(t) = r t \) for\( t \in [0, \infty) \)
- Uso de la ecuación de renovación
- Uso de transformaciones de Laplace
Solución
- La ecuación de renovación da\[ M(t) = 1 - e^{-r t} + \int_0^t M(t - s) r e^{-r s} \, ds \] Sustituir\( x = t - s \) en la integral da\[ M(t) = 1 - e^{-r t} + re^{-r t} \int_0^t M(x) e^{r x} \, dx \] Multiplicar a través por\( e^{ r t} \), diferenciar con respecto a\( t \), y simplificar da\( M^\prime(t) = r \) para\( t \ge 0 \). Ya que\( M(0) = 0 \), el resultado sigue.
- La transformación\( \Phi \) de Laplace de la distribución\( F \) viene dada por\[ \Phi(s) = \int_0^\infty e^{-s t} r e^{- r t} dt = \int_0^\infty rne^{-(s + r) t} dt = \frac{r}{r + s}, \quad s \in (0, \infty) \] Así que la transformación\( \Gamma \) de Laplace de la distribución\( M \) viene dada por\[ \Gamma(s) = \frac{\Phi(s)}{1 - \Phi(s)} = \frac{r}{s}, \quad s \in (0, \infty) \] Pero esta es la transformación de Laplace de la distribución\( t \mapsto r t \).
Demostrar que la vida actual y restante en el tiempo\( t \ge 0 \) satisfacen las siguientes propiedades:
- \( C_t \)y\( R_t \) son independientes.
- \( R_t \)tiene la misma distribución que un tiempo entre llegadas, es decir, la distribución exponencial con parámetro de tasa\( r \).
- \( C_t \)tiene una distribución exponencial truncada con parámetros\( t \) y\( r \):\[ \P(C_t \ge x) = \begin{cases} e^{-r x}, & 0 \le x \le t \\ 0, & x \gt t \end{cases} \]
Solución
Recordemos de nuevo eso\( M(t) = r t \) para\( t \in [0, \infty) \). Usando el resultado anterior sobre la distribución conjunta de la vida actual y restante, y algún cálculo estándar, tenemos\[ \P(C_t \ge x, R_t \ge y) = e^{-r (t + y)} + \int_0^{t - x} e^{-r(t + y - s)} r ds = r^{-r x} e^{-r y}, \quad x \in [0, t], \, y \in [0, \infty) \] Dejar\( y = 0 \) da\( \P(C_t \ge x) = e^{-r x} \) para\( x \in [0, t] \). Dejar\( x = 0 \) da\( \P(R_t \ge y) = e^{-r y} \) por\( y \in [0, \infty) \). Pero entonces también\( \P(C_t \ge x, R_t \ge y) = \P(C_t \ge x) \P(R_t \ge y) \) para\( x \in [0, t] \) y\( y \in [0, \infty) \) así las variables son independientes.
Juicios de Bernoulli
Considera el proceso de renovación para el cual los tiempos de interllegada tienen la distribución geométrica con parámetro\( p \). Recordemos que la función de densidad de probabilidad es\[ f(n) = (1 - p)^{n-1}p, \quad n \in \N_+ \] Las llegadas son los éxitos en una secuencia de ensayos de Bernoulli. El número de éxitos\( Y_n \) en los primeros\( n \) ensayos es la variable de conteo para\( n \in \N \). Las ecuaciones de renovación de esta sección pueden ser utilizadas para dar pruebas alternas de algunos de los resultados fundamentales en la Introducción.
Demostrar que la función de renovación es\( M(n) = n p \) para\( n \in \N \)
- Uso de la ecuación de renovación
- Uso de transformaciones de Laplace
Prueba
- La ecuación de renovación para\( M \) es\[ M(n) = F(n) + (M * F)(n) = 1 - (1 - p)^n + \sum_{k=1}^n M(n - k) p (1 - p)^{k-1}, \quad n \in \N \] Así sustituyendo valores de\( n \) sucesivamente tenemos\ begin {align} M (0) & = 1 - (1 - p) ^0 = 0\\ M (1) & = 1 - (1 - p) + M (0) p = p\\ M (2) & = 1 - (1 - p) ^2 + M (1) p + M (0) p (1 - p) 2 p\ end {align} y así sucesivamente.
- La transformación\( \Phi \) de Laplace de la distribución\( F \) es\[ \Phi(s) = \sum_{n=1}^\infty e^{-s n} p(1 - p)^{n-1} = \frac{p e^{-s}}{1 - (1 - p) e^{-s}}, \quad s \in (0, \infty) \] De ahí que la transformación de Laplace de la distribución\( s \mapsto e^{-s} \big/ (1 - e^{-s}) \) sea\[ \Gamma(s) = \frac{\Phi(s)}{1 - \Phi(s)} = p \frac{e^{-s}}{1 - e^{-s}}, \quad s \in (0, \infty) \] Pero\( M \) es la transformación de la distribución\( n \mapsto n \) en\( \N \). Es decir,\[ \sum_{n=1}^\infty e^{-s n} \cdot 1 = \frac{e^{-s}}{1 - e^{-s}}, \quad s \in (0, \infty) \]
Demostrar que la vida actual y restante en el tiempo\( n \in \N \) satisfacen las siguientes propiedades:.
- \( C_n \)y\( R_n \) son independientes.
- \( R_n \)tiene la misma distribución que un tiempo entre llegadas, es decir, la distribución geométrica con parámetro\( p \).
- \( C_n \)tiene una distribución geométrica truncada con parámetros\( n \) y\( p \):\[ \P(C_n = j) = \begin{cases} p (1 - p)^j, & j \in \{0, 1, \ldots, n-1\} \\ (1 - p)^n, & j = n \end{cases} \]
Solución
Recordemos de nuevo eso\( M(n) = p n \) para\( n \in \N \). Usando el resultado anterior sobre la distribución conjunta de la vida actual y restante y series geométricas, tenemos\[ \P(C_n \ge j, R_n \gt k) = (1 - p)^{n + k} + \sum_{i=1}^{n-j} p (1 - p)^{n + k - i} = (1 - p)^{j + k}, \quad j \in \{0, 1, \ldots, n\}, \, k \in \N \] Dejar\( k = 0 \) da\( \P(C_n \ge j) = (1 - p)^j \) para\( j \in \{0, 1, \ldots, n\} \). Dejar\( j = 0 \) da\( \P(R_n \gt k) = (1 - p)^k \) por\( k \in \N \). Pero entonces también\( \P(C_n \ge j, R_n \gt k) = \P(C_n \ge j) \P(R_n \gt k) \) para\( j \in \{0, 1, \ldots, n\} \) y\( k \in \N \) así las variables son independientes.
Una distribución Gamma Interarrival
Considere el proceso de renovación cuya distribución entre llegadas\( F \) es gamma con parámetro de forma\( 2 \) y parámetro de tasa\( r \in (0, \infty) \). Así\[ F(t) = 1 - (1 + r t) e^{-r t}, \quad t \in [0, \infty) \] Recordemos también que\( F \) es la distribución de la suma de dos variables aleatorias independientes, teniendo cada una la distribución exponencial con parámetro de tasa\( r \).
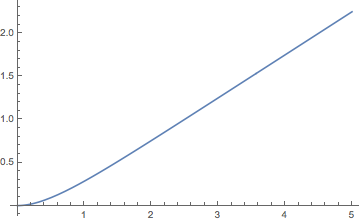
Demostrar que la función de distribución de renovación\( M \) viene dada por\[ M(t) = -\frac{1}{4} + \frac{1}{2} r t + \frac{1}{4} e^{- 2 r t}, \quad t \in [0, \infty) \]
Solución
La distribución exponencial con parámetro de tasa\( r \) tiene transformada de Laplace\( s \mapsto r \big/ (r + s) \) y por lo tanto la transformada\( \Phi \) de Laplace de la distribución\( F \) interarrival viene dada por\[ \Phi(s) = \left(\frac{r}{r + s}\right)^2 \] Entonces la transformada\( \Gamma \) de Laplace de la distribución\( M \) es\[ \Gamma(s) = \frac{\Phi(s)}{1 - \Phi(s)} = \frac{r^2}{s (s + 2 r)} \] Usando un parcial descomposición de la fracción,\[ \Gamma(s) = \frac{r}{2 s} - \frac{r}{2 (s + 2 r)} = \frac{1}{2} \frac{r}{s} - \frac{1}{4} \frac{2 r }{s + 2 r} \] Pero la\( r / s \) es la transformada de Laplace de la distribución\( r t \) y\( 2 r \big/(s + 2 r ) \) es la transformada de Laplace de la distribución\( 1 - e^{-2 r t} \) (la distribución exponencial con parámetro\( 2 r \)).
Tenga en cuenta que\( M(t) \approx -\frac{1}{4} + \frac{1}{2} r t \) como\( t \to \infty \).
Abra el experimento de renovación y seleccione la distribución gamma interllegada con el parámetro de forma\( k = 2 \) y el parámetro de escala\( b = 1 \) (por lo que el parámetro de tasa también\( r = \frac{1}{b} \) es 1). Para cada uno de los siguientes valores del parámetro de tiempo, ejecute el experimento 1000 veces y anote la forma y ubicación de la distribución empírica de la variable de conteo.
- \( t = 5 \)
- \( t = 10 \)
- \( t = 15 \)
- \( t = 20 \)
- \( t = 25 \)
- \( t = 30 \)


