1.3: Interpretaciones
- Page ID
- 150996
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)¿Qué es Probabilidad?
El sistema formal de probabilidad es un modelo cuya utilidad sólo puede establecerse examinando su estructura y determinando si los patrones de incertidumbre y verosimilitud en alguna situación práctica pueden representarse adecuadamente. Con la excepción del evento seguro y el evento imposible, el modelo no nos dice cómo asignar probabilidad a un evento dado. El sistema formal es consistente con muchas asignaciones de probabilidad, así como la noción de masa es consistente con muchas asignaciones de masa diferentes a conjuntos en el espacio básico.
Las propiedades definitorias (P1), (P2), (P3) y las propiedades derivadas proporcionan reglas de consistencia para realizar asignaciones de probabilidad. No se pueden asignar probabilidades negativas o probabilidades mayores a una. Al evento seguro se le asigna probabilidad uno. Si dos o más eventos son mutuamente excluyentes, la probabilidad total asignada a la unión debe ser igual a la suma de las probabilidades de los eventos separados. Se permite cualquier asignación de probabilidad consistente con estas condiciones.
Es posible que no se conozca la asignación de probabilidad a cada evento. Así como las condiciones definitorias ponen restricciones a las asignaciones de probabilidad permisibles, también proporcionan una estructura importante. Un problema típico aplicado proporciona las probabilidades de los miembros de una clase de eventos (quizás solo unos pocos) a partir de los cuales determinar las probabilidades de otros eventos de interés. Consideramos una clase importante de tales problemas en el próximo capítulo.
Existe una variedad de puntos de vista sobre cómo se debe interpretar la probabilidad. Estos impactan en la manera en que se asignan (o asumen) las probabilidades. Una dicotomía importante entre los practicantes.
- Un grupo cree que la probabilidad es objetiva en el sentido de que es algo inherente a la naturaleza de las cosas. Se va a descubrir, si es posible, por análisis y experimento. Ya sea que podamos determinarlo o no, “está ahí”.
- Otro grupo insiste en que la probabilidad es una condición de la mente de la persona que realiza la evaluación de probabilidad. Desde este punto de vista, las leyes de probabilidad simplemente imponen consistencia racional a la manera en que se asigna probabilidades a los eventos. Se han hecho diversos intentos para encontrar formas objetivas de medir la fuerza de la propia creencia o grado de certeza de que ocurrirá un evento. La probabilidad\(P(A)\) expresa el grado de certeza que uno siente que el evento A ocurrirá. Un enfoque para caracterizar el grado de certeza de un individuo es equiparar su valoración\(P(A)\) con la cantidad a que está dispuesto a pagar para jugar un juego que devuelve una unidad de dinero si A se produce, para una ganancia de\((1 - a)\), y devuelve cero si A no ocurrir, para una ganancia de\(-a\). Detrás de esta formulación está la noción de un juego limpio, en el que la ganancia “esperada” o “promedio” es cero.
El trabajo temprano sobre la probabilidad comenzó con un estudio de las frecuencias relativas de ocurrencia de un evento bajo ensayos repetidos pero independientes. Esta idea está tan incrustada en un pensamiento muy intuitivo sobre la probabilidad que algunos probabilistas han insistido en que debe integrarse en la definición de probabilidad. Este enfoque no ha sido del todo exitoso matemáticamente y no ha atraído mucho seguimiento entre los probabilistas teóricos o aplicados. En el modelo que adoptamos, existe un teorema de límite fundamental, conocido como teorema de Borel, que puede interpretarse “si un ensayo se realiza un gran número de veces de manera independiente, la fracción de veces que\(A\) ocurre el evento se acerca como límite el valor \(P(A)\). Establecer este resultado (que no hacemos en este tratamiento) proporciona una validación formal de la noción intuitiva que se esconde detrás de los primeros intentos de formular probabilidades. Los jugadores empedernidos habían notado regularidades estadísticas a largo plazo y buscaron explicaciones de sus amigos matemáticamente dotados. Desde este punto de vista, la probabilidad es significativa sólo en situaciones repetibles. Quienes sostienen este punto de vista suelen asumir una visión objetiva de la probabilidad. Se trata de un número determinado por la naturaleza de la realidad, para ser descubierto por experimentos repetidos.
Existen muchas aplicaciones de probabilidad en las que el punto de vista de la frecuencia relativa no es factible. Los ejemplos incluyen predicciones del clima, el resultado de un juego o una carrera de caballos, el desempeño de un individuo en un trabajo en particular, el éxito de una computadora de nuevo diseño. Se trata de ensayos únicos e irrepetibles. Como lo tiene la expresión popular, “Sólo se da la vuelta una vez”. En ocasiones, las probabilidades en estas situaciones pueden ser bastante subjetivas. De hecho, quienes adoptan una visión subjetiva tienden a pensar en términos de tales problemas, mientras que quienes adoptan una visión objetiva suelen enfatizar la interpretación de frecuencia.
Probabilidad subjetiva y un partido de fútbol
La probabilidad de que el equipo de fútbol favorito de uno gane el próximo Juego de la Superbowl bien puede ser solo una probabilidad subjetiva del apostador. Esto ciertamente no es una probabilidad que pueda ser determinada por un gran número de ensayos repetidos. El juego sólo se juega una vez. Sin embargo, la evaluación subjetiva de las probabilidades puede basarse en el conocimiento íntimo de las fortalezas y debilidades relativas de los equipos involucrados, así como factores como el clima, las lesiones y la experiencia. Puede haber una base objetiva considerable para la asignación subjetiva de probabilidad. De hecho, a menudo hay un elemento “frecuentista” oculto en la evaluación subjetiva. Existe una evaluación (quizás no realizada) de que en situaciones similares las frecuencias tienden a coincidir con el valor asignado subjetivamente.
La probabilidad de la lluvia
Los noticieros suelen informar que la probabilidad de lluvia de es de 20 por ciento o 60 por ciento o alguna otra cifra. Aquí hay varias dificultades.
- Para utilizar el modelo matemático formal, debe haber precisión en la determinación de un evento. Un evento o bien ocurre o no lo hace. ¿Cómo determinamos si ha llovido o no? ¿Debe haber una cantidad medible? ¿Dónde debe caer esta lluvia para contabilizarse? ¿Durante qué periodo de tiempo? Incluso si hay acuerdo sobre el área, la cantidad, y el periodo de tiempo, queda ambigüedad: no se puede decir con certeza lógica que el evento ocurrió o no ocurrió. Sin embargo, en esta y otras situaciones similares, el uso del concepto de un evento puede ser útil aunque la descripción no sea definitiva. Por lo general hay suficiente acuerdo práctico para que el concepto sea útil.
- ¿Qué significa una probabilidad de lluvia del 30 por ciento? ¿Significa que si la predicción es correcta, el 30 por ciento del área indicada recibirá lluvia (en una cantidad acordada) durante el periodo de tiempo especificado? ¿O significa que el 30 por ciento de las ocasiones en que se haga tal predicción habrá precipitaciones significativas en la zona durante el periodo de tiempo especificado? Nuevamente, esta última alternativa bien puede ocultar una interpretación de frecuencia. ¿Significa el comunicado que llueve 30 por ciento de las veces en que las condiciones son similares a las actuales?
Independientemente de la interpretación, existe cierta ambigüedad sobre el suceso y si ha ocurrido. Y hay alguna dificultad para saber interpretar la cifra de probabilidad. Si bien el significado preciso de una probabilidad de lluvia del 30 por ciento puede ser difícil de determinar, generalmente es útil saber si las condiciones conducen a una asignación de 20 por ciento o 30 por ciento o 40 por ciento de probabilidad. Y no cabe duda de que a medida que la tecnología y metodología de predicción meteorológica sigan mejorando las evaluaciones de probabilidad meteorológica serán cada vez más útiles.
Otro tipo común de situación de probabilidad consiste en determinar la distribución de alguna característica sobre una población, generalmente mediante una encuesta. Estos datos se utilizan para responder a la pregunta: ¿Cuál es la probabilidad (probabilidad) de que un miembro de la población, elegido “al azar” (es decir, sobre una base igualmente probable) tenga cierta característica?
Probabilidad empírica basada en datos de encuestas
Una encuesta hace dos preguntas a 300 alumnos: ¿Vives en el campus? ¿Estás satisfecho con las instalaciones recreativas del centro estudiantil? Las respuestas a esta última pregunta se clasificaron como “razonablemente satisfechas”, “insatisfechas” o “sin opinión definitiva”. Que\(C\) sea el evento “en el campus”;\(O\) sea el evento “fuera del campus”;\(S\) sea el evento “razonablemente satisfecho”;\(U\) sea el evento” insatisfecho;” y\(N\) ser el evento “sin opinión definitiva”. Los datos se muestran en la siguiente tabla.
Datos de la Encuesta
| S | U | N | |
| C | 127 | 31 | 42 |
| O | 46 | 43 | 11 |
Si un individuo es seleccionado de manera igualmente probable de este grupo de 300, la probabilidad de cualquiera de los eventos se toma como la frecuencia relativa de los encuestados en cada categoría correspondiente a un evento. Hay 200 miembros en el campus en la población, así\(P(C) = 200/300\) y\(P(O) = 100/300\). Se toma como ser la probabilidad de que un estudiante seleccionado esté en el campus y satisfecho\(P(CS) = 127/300\). La probabilidad de que un estudiante esté en el campus y satisfecho o fuera del campus y no esté satisfecho es
\(P(CS \bigvee OU) = P(CS) + P(OU) = 127/300 + 43/300 = 170/300\)
Si hay razones para creer que la población muestreada es representativa de todo el cuerpo estudiantil, entonces se aplicarían las mismas probabilidades a cualquier estudiante seleccionado al azar de todo el alumnado.
Es una suerte que no tengamos que declarar una sola posición para ser el punto de vista e interpretación “correctos”. El modelo formal es congruente con cualquiera de los puntos de vista expuestos. Somos libres en cualquier situación de hacer la interpretación más significativa y natural al problema que nos ocupa. No es necesario encajar todos los problemas en un solo molde conceptual; ni es necesario cambiar el modelo matemático cada vez que un punto de vista diferente parece apropiado.
Probabilidad y cuotas
A menudo nos resulta conveniente trabajar con una proporción de probabilidades. Si\(A\) y\(B\) son eventos con probabilidad positiva, las probabilidades que\(A\) favorecen\(B\) es la razón de probabilidad\(P(A)P(B)\). Si no se especifica lo contrario,\(B\) se toma como ser\(A^c\) y hablamos de las cuotas que favorecen\(A\)
\(O(A) = \dfrac{P(A)}{P(A^c)} = \dfrac{P(A)}{1 - P(A)}\)
Esta expresión puede resolverse algebraicamente para determinar la probabilidad a partir de las probabilidades
\(P(A) = \dfrac{O(A)}{1 + O(A)}\)
En particular, si\(O(A) = a/b\) entonces\(P(A) = \dfrac{a/b}{1+a/b} = \dfrac{a}{a+b}\).
\(O(A) = 0.7/0.3 = 7/3\). Si las probabilidades que favorecen\(A\) son 5/3, entonces\(P(A) = 5/(5 + 3) = 5/8\).
Particiones y combinaciones booleanas de eventos
La propiedad de aditividad contable (P3) otorga una prima a la partición adecuada de los eventos.
Definición
Una partición es una clase mutuamente excluyente
\({A_i : i \in J}\)de tal manera que\(\Omega = \bigvee_{i \in J} A_i\)
Una partición de evento\(A\) es una clase mutuamente excluyente
\({A_i : i \in J}\)de tal manera que\(A = \bigvee_{i \in J} A_i\)
Observaciones.
- Una partición es una clase de eventos mutuamente excluyentes de tal manera que uno (y solo uno) debe ocurrir en cada juicio.
- Una partición de evento\(A\) es una clase de eventos mutuamente excluyentes tal que\(A\) ocurre si uno (y solo uno) de los\(A_i\) ocurre.
- Una partición (sin calificador) se toma como una partición del evento sure\(\Omega\).
- Si la clase\({B_i : i \in J}\) es mutuamente excluyente y\(A \subset B = \bigvee_{i \in J} B_i\), entonces la clase\({AB_i : i \in J}\) es una partición de\(A\) y\(A = \bigvee_{i \in J} AB_i\).
Podemos comenzar con una secuencia\({A_1: 1 \le i}\) y determinar una secuencia mutuamente excluyente (disjunta) de la\({B_1: 1 \le i}\) siguiente manera:
\(B_1 = A_1\), y para cualquier\(i > 1\),\(B_i = A_i A_{1}^{c} A_{2}^{c} \cdot\cdot\cdot A_{i - 1}^{c}\)
Así cada uno\(B_i\) es el conjunto de esos elementos de\(A_i\) no en ninguno de los miembros anteriores de la secuencia.
Esta representación se utiliza para mostrar que la subaditividad (P9) se deriva de la aditividad y propiedad contables (P6). Desde cada uno\(B_i \subset A_i\), por (P6)\(P(B_i) \le P(A_i)\). Ahora
\(P(\bigcup_{i = 1}^{\infty} A_i) = P(\bigvee_{i = 1}^{\infty} B_i) = \sum_{i = 1}^{\infty} P(B_i) \le \sum_{i = 1}^{\infty} P(A_i)\)
La representación de una unión como unión disjunta apunta a una estrategia importante en la solución de problemas de probabilidad. Si un evento puede expresarse como una unión disjunta contable de eventos, cada una de cuyas probabilidades se conoce, entonces la probabilidad de la combinación es la suma de las probabilidades individuales. En el módulo sobre Particiones y Minterms, mostramos que cualquier combinación booleana de una clase finita de eventos puede expresarse como una unión disjunta de una manera que a menudo facilita la determinación sistemática de las probabilidades.
La función del indicador
Una de las herramientas más útiles para tratar con combinaciones de conjuntos (y por lo tanto con combinaciones de eventos) es la función de indicador\(I_E\) para un conjunto\(E \subset \Omega\). Se define de manera muy simple de la siguiente manera:
\(I_E (\omega) = \begin{cases}1 & \text{for } \omega \in E \\ 0 & \text{for } \omega \in E^c \end{cases}\)
Observación. Las funciones de indicador pueden definirse en cualquier dominio. Tenemos ocasión en diversos casos de definirlos en la línea real y en espacios euclidianos de dimensiones superiores. Por ejemplo, si\(M\) es el intervalo [\(a,b\)] en la línea real entonces\(I_M(t) = 1\) para cada uno\(t\) en el intervalo (y es cero en caso contrario). Así tenemos una función de paso con valor unitario sobre el intervalo\(M\). En el espacio básico abstracto no\(\Omega\) podemos dibujar una gráfica tan fácilmente. Sin embargo, con la representación de conjuntos en un diagrama de Venn, podemos dar una representación esquemática, como en la Figura 1.3.1.
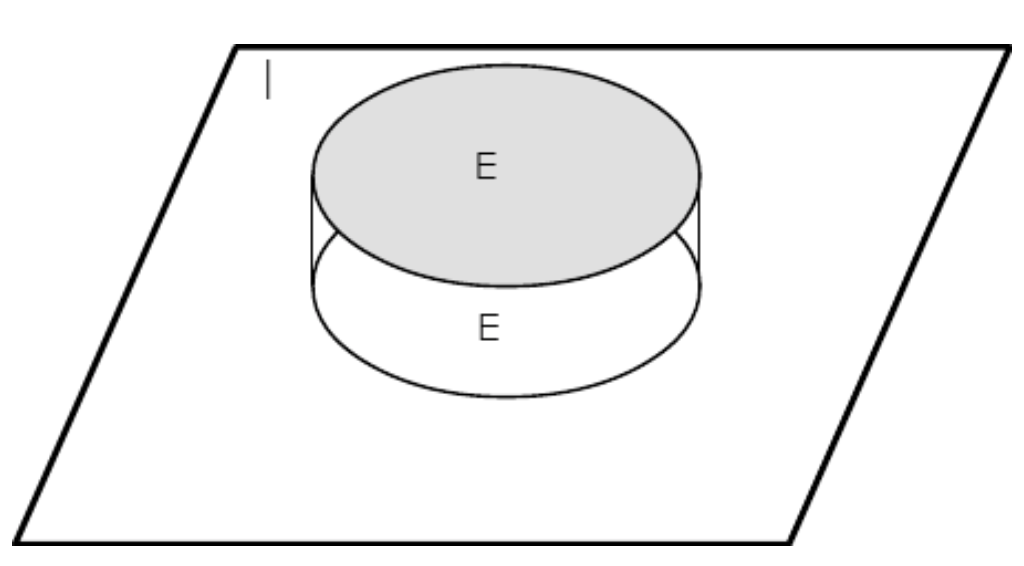
Figura 1.3.1. Representación de la función indicadora\(I_E\) para evento\(E\).
Gran parte de la utilidad de la función indicadora proviene de las siguientes propiedades.
(IF1):\(I_A \le I_B\) iff\(A \subset B\). Si\(I_A \le I_B\), entonces\(\omega \in A\) implica\(I_A (\omega) = I_B (\omega) = 1\)\(\omega \in B\), entonces\(I_A (\omega) = 1\) implica\(\omega \in A\)\(\omega \in B\) implica\(I_B (\omega) = 1\).
(IF2):\(I_A = I_B\) iff\(A = B\)
\(A = B\)iff ambos\(A \subset B\) e\(B \subset A\) iff\(I_A \le I_B\) e\(I_B \le I_A\) iff\(I_A = I_B\)
(IF3):\(I_{A^c} = 1 - I_A\) Esto se desprende del hecho\(I_{A^c} (\omega) = 1\) iff\(I_A (\omega) = 0\).
(IF4):\(I_{AB} = I_A I_B = \text{min } {I_A, I_B}\) (se extiende a cualquier clase) Un elemento ω pertenece a la intersección iff pertenece a todos iff la función indicadora para cada evento es uno iff el producto de las funciones indicadoras es uno.
(IF5):\(I_{A \cup B} = I_A + I_B - I_A I_B = \text{min }{I_A, I_B}\) (la regla máxima se extiende a cualquier clase) La regla máxima se desprende del hecho de que\(\omega\) está en la unión si está en uno o más de los eventos en la unión iff cualquiera o más de la función indicadora individual tiene valor uno iff el máximo es uno. La regla de suma para dos eventos es establecida por la regla y las propiedades de DeMorgan (IF2), (IF3) e (IF4) de DeMorgan.
\(I_{A \cup B} = 1 - I_{A^c B^c} = 1 - [1 - I_A][1 - I_B] = 1 - 1 + I_B + I_A - I_A I_B\)
(IF6): Si el par\({A, B}\) es disjunta,\(I_{A \bigvee B} = I_A+ I_B\) (se extiende a cualquier clase disjunta)
El siguiente ejemplo ilustra el uso de funciones de indicador en el establecimiento de relaciones entre combinaciones de conjuntos. Otros usos y técnicas se establecen en el módulo sobre Particiones y Mintérms.
Funciones de indicador y combinaciones de conjuntos
Supongamos que\({A_i : 1 \le i \le n}\) es una partición.
Si\(B = \bigvee_{i = 1}^{n} A_i C_i\), entonces\(B^c = \bigvee_{i = 1}^{n} A_i C_{i}^{c}\)
- Prueba
-
Utilizando las propiedades de la función indicadora establecida anteriormente, tenemos
\(I_B = \sum_{i = 1}^{n} I_{A_i} I_{C_i}\)
Tenga en cuenta que desde la\(A_i\) forma una partición, tenemos\(\sum_{i = 1}^{n} I_{A_i} = 1\), por lo que la función indicadora para el evento complementario es
\(I_{B^c} = 1 - \sum_{i = 1}^{n} I_{A_i} I_{C_i} = \sum_{i = 1}^{n} I_{A_i} - \sum_{i = 1}^{n} I_{A_i} I_{C_i} = \sum_{i = 1}^{n} [1 - I_{C_i}] = \sum_{i = 1}^{n} I_{A_i} I_{C_{i}^{c}}\)
La última suma es la función indicadora para\(\bigvee_{i = 1}^{n} A_i C_{i}^{c}\)
Un comentario técnico sobre la clase de eventos
La clase de eventos juega un papel central en el fondo intuitivo, la aplicación y la estructura matemática formal. Los eventos han sido modelados como subconjuntos del espacio básico de todos los posibles resultados del ensayo o experimento. En el caso de un número finito de resultados, cualquier subconjunto puede ser tomado como un evento. En la teoría general, implicando infinitas posibilidades, existen algunas razones técnicas matemáticas para limitar la clase de subconjuntos a ser considerados como eventos. Las necesidades prácticas son las siguientes:
- Si\(A\) es un evento, su conjunto complementario también debe ser un evento.
- Si\({A_i : i \in J}\) es una clase finita o contable de eventos, la unión y la intersección de los miembros de la clase necesitan ser eventos.
Un argumento simple basado en las reglas de DeMorgan muestra que si la clase contiene complementos de todos sus conjuntos y uniones contables, entonces contiene intersecciones contables. De igual manera, si contiene complementos de todos sus conjuntos e intersecciones contables, entonces contiene uniones contables. Una clase de conjuntos cerrados bajo complementos y uniones contables se conoce como álgebra sigma de conjuntos. En un tratamiento formal teórico de medidas, una suposición básica es que la clase de eventos es un álgebra sigma y la medida de probabilidad asigna probabilidades a los miembros de esa clase. Tal clase es tan general que se necesitan argumentos muy sofisticados para establecer el hecho de que tal clase no contiene todos los subconjuntos. Pero precisamente porque la clase es tan general e inclusiva en las aplicaciones ordinarias no necesitamos preocuparnos por qué conjuntos son permisibles como eventos
Una tarea primordial en la formulación de un problema de probabilidad es identificar los eventos apropiados y las relaciones entre ellos. El tratamiento teórico muestra que podemos trabajar con gran libertad en la formación de eventos, con la seguridad de que en la mayoría de las aplicaciones un conjunto así producido es un evento matemáticamente válido. La llamada pregunta de mensurabilidad solo entra en juego al tratar procesos aleatorios con parámetros continuos. Incluso ahí, bajo supuestos razonables, los conjuntos producidos serán eventos.


