2.1: Minterms
- Page ID
- 150928
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Particiones y minterms
Para ver cómo surge naturalmente la partición fundamental, considera primero la partición del espacio básico producido por un solo evento\(A\).
\[\Omega = A \bigvee A^c\]
Ahora si\(B\) es un segundo evento, entonces
\[A = AB \bigvee AB^c\]
y
\[A^c = A^c B \bigvee A^c B^c\]
para que
\[\Omega = A^c B^c \bigvee A^c B \bigvee AB^c \bigvee AB\]
El par se\(\{A, B\}\) ha\(\Omega\) dividido en\(\{A^c B^c, A^c B, AB^c, AB\}\). La continuación es así que conduce sistemáticamente a una partición por tres eventos\(\{A, B, C\}\), cuatro eventos\(\{A, B, C, D\}\), etc.
Ilustramos los patrones fundamentales en el caso de cuatro eventos\(\{A, B, C, D\}\). Formamos los minterms como intersecciones de miembros de la clase, con diversos patrones de complementación. Para una clase de cuatro eventos, existen\(2^4 = 16\) tales patrones, de ahí 16 minterms. Estas son, en un arreglo sistemático,
| \(A^c B^c C^c D^c\) | \(A^c B C^c D^c\) | \(A B^c C^c D^c\) | \(A B C^c D^c\) |
| \(A^c B^c C^c D\) | \(A^c B C^c D\) | \(A B^c C^c D\) | \(A B C^c D\) |
| \(A^c B^c C D^c\) | \(A^c B C D^c\) | \(A B^c C D^c\) | \(A B C D^c\) |
| \(A^c B^c C D\) | \(A^c B C D\) | \(A B^c C D\) | \(A B C D\) |
Ningún elemento puede estar en más de un minterm, porque cada uno difiere de los demás por la complementación de al menos un evento miembro. Cada elemento\(\omega\) se asigna exactamente a uno de los minterms determinando las respuestas a cuatro preguntas:
¿Está en\(A\)? ¿Está en\(B\)? ¿Está en\(C\)? ¿Está en\(D\)?
Supongamos, por ejemplo, las respuestas son: Sí, No, No, Sí. Entonces ω está en el minterm\(A B^c C^c D\). De manera similar, podemos determinar la pertenencia de cada uno\(\omega\) en el espacio básico. Así, los minterms forman una partición. Es decir, los minterms representan eventos mutuamente excluyentes, uno de los cuales seguramente ocurrirá en cada juicio. La pertenencia a cualquier minterm depende de la pertenencia a cada grupo generador\(A, B, C\) o\(D\), y de las relaciones entre ellos. Para algunas clases, uno o más de los minterms están vacíos (eventos imposibles). Como vemos a continuación, esto no causa problemas.
Un examen del desarrollo anterior muestra que si comenzamos con una clase de n eventos, hay\(2^n\) minterms. Para ayudar en el manejo sistemático, introducimos un sistema de numeración simple para los minterms, que ilustramos considerando nuevamente los cuatro eventos\(A, B, C, D\), en ese orden. Las respuestas a las cuatro preguntas anteriores pueden ser representadas numéricamente por el esquema
No\(\sim 0\) y Sí\(\sim 1\)
Así, si\(\omega\) está en\(A^c B^c C^c D^c\), las respuestas se tabulan como 0 0 0 0 0. Si\(\omega\) está en\(A B^c C^c D\), entonces esto se designa 1 0 0 1. Con este esquema, el arreglo minterm anterior se convierte
| 0000\(\sim\) 0 | 0100\(\sim\) 4 | 1000\(\sim\) 8 | 1100\(\sim\) 12 |
| 0001\(\sim\) 1 | 0101\(\sim\) 5 | 1001\(\sim\) 9 | 1101\(\sim\) 13 |
| 0010\(\sim\) 2 | 0110\(\sim\) 6 | 1010\(\sim\) 10 | 1110\(\sim\) 14 |
| 0011\(\sim\) 3 | 0111\(\sim\) 7 | 1011\(\sim\) 11 | 1111\(\sim\) 15 |
Podemos ver estos cuatriples de ceros y unos como representaciones binarias de enteros, que también pueden estar representados por sus equivalentes decimales, como se muestra en la tabla. Frecuentemente, es útil referirse a los minterms por número. Si los miembros de la clase generadora son tratados en un orden fijo, entonces cada número minterm al que se llega de la manera anterior especifica un minterm de manera única. Así, para la clase generadora\(\{A, B, C, D\}\), en ese orden, podemos designar
\(A^c B^c C^c D^c = M_0\)(minterm 0)\(AB^cC^c D = M_9\) (minterm 9), etc.
Utilizamos este esquema de numeración en diagramas especiales de Venn llamados mapas minterm. Estos se ilustran en la Figura, para los casos de tres, cuatro y cinco eventos generadores. Dado que el contenido real de cualquier minterm depende de los conjuntos\(A, B, C\), y\(D\) en la clase generadora, es costumbre referirse a estos conjuntos como variables. En el caso de tres variables, set\(A\) es la mitad derecha del diagrama y set\(C\) es la mitad inferior; pero el conjunto B está dividido, de manera que es la unión de la segunda y cuarta columnas. Divisiones similares ocurren en los otros casos.
OBSERVACIÓN. Otras disposiciones útiles de mapas minterm se emplean en el análisis de circuitos de conmutación.
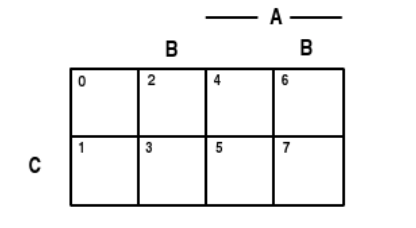
Tres variables
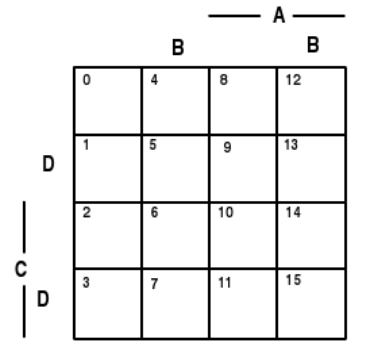
Cuatro variables
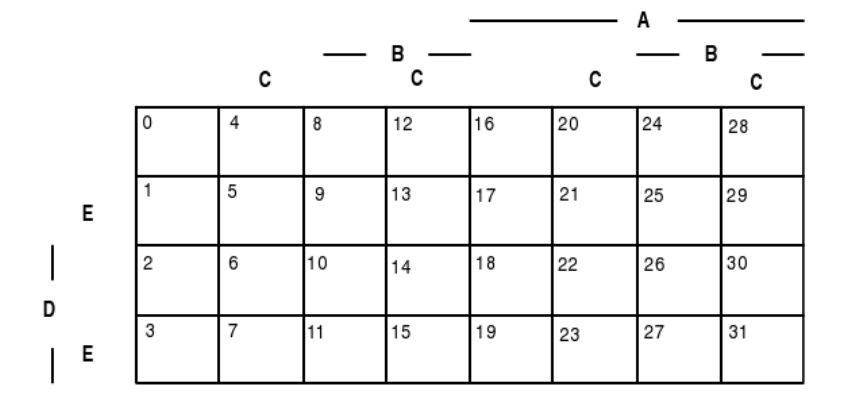
Cinco variables
Figura 2.1.1. Mapas minterm para tres, cuatro o cinco variables
Mapas minterm y la expansión minterm
La importancia de la partición minterm del espacio básico descansa en gran medida en el siguiente hecho.
Expansión Minterm
Cada combinación booleana de los elementos en una clase generadora puede expresarse como la unión disjunta de una subclase apropiada de los minterms. Esta representación se conoce como la expansión minterm para la combinación.
Al derivar una expresión para una combinación booleana dada que se mantiene para cualquier clase\(\{A, B, C, D\}\) de cuatro eventos, incluimos todos los minterms posibles, ya sean vacíos o no. Si un minterm está vacío para una clase dada, su presencia no modifica el contenido establecido o la asignación de probabilidad para la combinación booleana.
La existencia y singularidad de la expansión se hace plausible por ejemplos simples que utilizan mapas minterm para determinar gráficamente el contenido minterm de varias combinaciones booleanas. Usando el sistema de arreglo y numeración introducido anteriormente, dejamos\(M_i\) representar el\(i\) th minterm (numeración desde cero) y dejamos\(p(i)\) representar la probabilidad de ese minterm. Cuando tratamos una unión de minterms en una expansión minterm, es conveniente utilizar la taquigrafía ilustrada a continuación.
\(M(1, 3, 7) = M_1 \bigvee M_3 \bigvee M_7\)y\(p(1, 3, 7) = p(1) + p(3) + p(7)\)
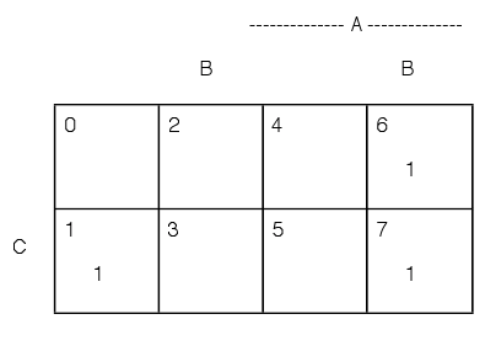
Figura 2.1.2. \(E = AB \cup A^c (B \cup C^c)^c = M(1:6, 7)\)Expansión a corto plazo para el Ejemplo 2.1.1
Considera el siguiente ejemplo sencillo.
Ejemplo\(\PageIndex{1}\) Minterm expansion
Supongamos\(E = AB \cup A^c (B \cup C^c)^c\). El examen del mapa minterm en la Figura 2.1.2 muestra que\(AB\) consiste en la unión de minterms\(M_6\),\(M_7\), que designamos\(M(6,7)\). La combinación\(B \cup C^c = M(0, 2, 3, 4, 6, 7)\), para que su complemento\((B \cup C^c)^c = M(1, 5)\). Esto deja la parte comón\(A^c (B \cup C^c)^c = M_1\), Por lo tanto,\(E = M(1, 6, 7)\). De igual manera,\(F = A \cup B^c C = M(1, 4, 5, 6, 7)\).
Una clave para establecer la expansión es señalar que cada minterm es un subconjunto de la combinación o es disjunta de ella. La expansión es así la unión de aquellos minterms incluidos en la combinación. En la última sección de este módulo se esboza una verificación general mediante funciones indicadoras.
Uso de mapas minterm
Un problema típico busca la probabilidad de ciertas combinaciones booleanas de una clase de eventos cuando se dan las probabilidades de varias otras combinaciones. Consideramos varios ejemplos simples e ilustramos el uso de mapas minterm en formulación y solución.
Ejemplo\(\PageIndex{2}\) Survey on software
Los datos estadísticos se toman para cierta población estudiantil con computadoras personales. Se selecciona al azar a un individuo. Deje que\(A =\) el evento que la persona seleccionada tenga procesamiento de textos,\(B =\) el evento que tenga un programa de hoja de presentación y\(C =\) el evento que la persona tenga un programa de base de datos. Los datos implican
- La probabilidad es 0.80 de que la persona tenga un programa de procesamiento de textos:\(P(A) = 0.8\)
- La probabilidad es 0.65 de que la persona tenga un programa de hoja de cálculo:\(P(B) = 0.65\)
- La probabilidad es 0.30 de que la persona tenga un programa de base de datos:\(P(C) = 0.3\)
- La probabilidad es 0.10 de que la persona tenga los tres:\(P(ABC) = 0.1\)
- La probabilidad es 0.05 de que la persona no tenga procesamiento de textos ni pliego:\(P(A^c B^c = 0.05\)
- La probabilidad es 0.65 de que la persona tenga al menos dos:\(P(AB \cup AC \cup BC) = 0.65\)
- La probabilidad de procesador de textos y base de datos, pero ninguna hoja de cálculo es el doble de probabilidad de hoja de cálculo y base de datos, pero no procesador de textos:\(P(AB^cC) = 2P(A^cBC)\)
a. ¿Cuál es la probabilidad de que la persona tenga exactamente dos de los programas?
b. ¿Cuál es la probabilidad de que la persona tenga únicamente el programa base de datos?
Surgen varias preguntas:
- ¿Estos datos son consistentes?
- ¿Los datos son suficientes para responder a las preguntas?
- ¿Cómo se pueden utilizar los datos para resolver las preguntas?
Solución
Los datos, expresados en términos de probabilidades minterm, son:
\(P(A) = p(4, 5, 6, 7) = 0.80\); por lo tanto\(P(A^c) = p(0, 1, 2, 3) = 0.20\)
\(P(B) = p(2, 3, 6, 7) = 0.65\); por lo tanto\(P(B^c) = p(0, 1, 4, 5) = 0.35\)
\(P(C) = p(1, 3, 5, 7) = 0.30\); por lo tanto\(P(C^c) = p(0, 2, 4, 6) = 0.70\)
\(P(ABC) = p(7) = 0.10\)\(P(A^c B^c) = p(0, 1) = 0.05\)
\(P(AB \cup AC \cup BC) = p(3, 5, 6, 7) = 0.65\)
\(P(AB^c C) = p(5) = 2p(3) = 2P(A^c BC)\)
Estos datos se muestran en el mapa minterm en la Figura 2.1.3 a. Utilizamos los patrones mostrados en el mapa minterm para ayudar en una solución algebraica para las diversas probabilidades minterm.
\(p(2, 3) = p(0, 1, 2, 3) - p(0, 1) = 0.20 - 0.05 = 0.15\)
\(p(6,7) = p(2, 3, 6, 7) - p(2, 3) = 0.65 - 0.15 = 0.50\)
\(p(6) = p(6,7) - p(7) = 0.50 - 0.10 = 0.40\)
\(p(3,5) = p(3, 5, 6, 7) - p(6,7) = 0.65 -0.50 = 0.15 \Rightarrow p(3) = 0.05\),
\(p(5) = 0.10 \Rightarrow p(2) = 0.10\)
\(p(1) = p(1, 3, 5, 7) - p(3, 5) - p(7) = 0.30 - 0.15 - 0.10 = 0.05 \Rightarrow p(0) = 0\)
\(p(4) = p(4, 5, 6, 7) - p(5) - p(6, 7) = 0.80 - 0.10 - 0.50 = 0.20\)
Así, se determinan todas las probabilidades minterm. Se muestran en la Figura 2.1.3 b. De estos obtenemos
\(P(A^c BC \bigvee AB^cC \bigvee ABC^c) = p(3, 5, 6) = 0.05 + 0.10 + 0.40 = 0.55\)y\(P(A^c B^c C) = p(1) = 0.05\)
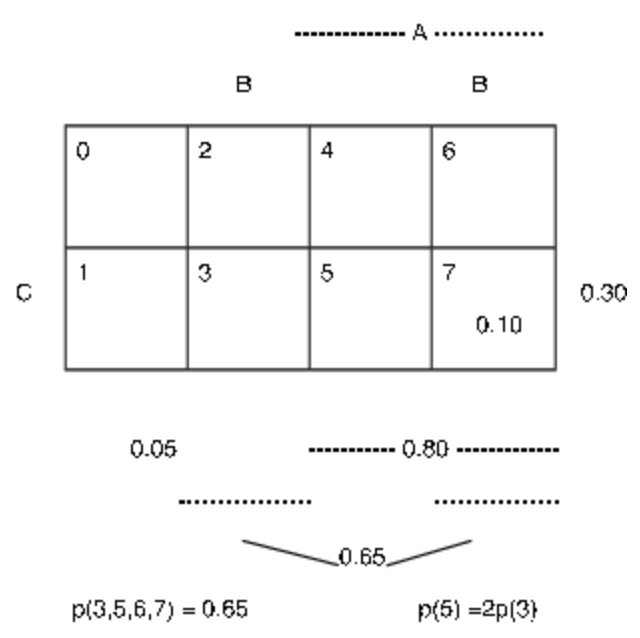
a. Datos para encuesta por software, Ejemplo 2.3.1
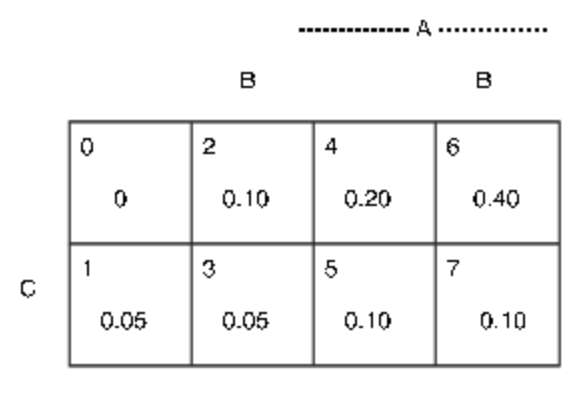
b. Probabilidades minterm para encuestas por software. Ejemplo 3.3.1
Figura 2.1.3. Mapas minterm para levantamiento por software.
Ejemplo\(\PageIndex{3}\) Survey on personal computers
Una encuesta a 1000 estudiantes muestra que 565 tienen computadoras de escritorio compatibles con PC, 515 tienen computadoras de escritorio Macintosh y 151 tienen computadoras portátiles. 51 tienen las tres, 124 tienen computadoras tanto PC como portátiles, 212 tienen al menos dos de las tres, y el doble de poseen tanto PC como portátiles que quienes tienen ambas Computadora de escritorio y portátil Macintosh. Se selecciona al azar a una persona de esta población. ¿Cuál es la probabilidad de que tenga al menos uno de estos tipos de computadoras? ¿Cuál es la probabilidad de que la persona seleccionada tenga solo una computadora portátil?
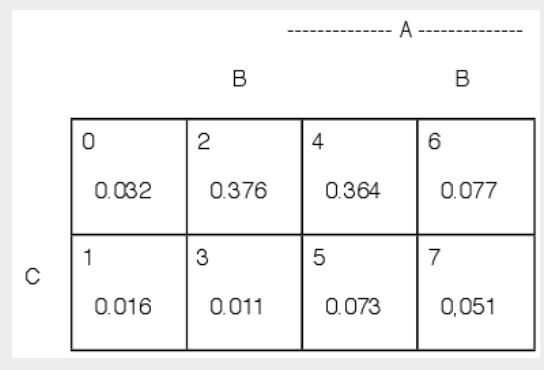
Figura 2.1.4. Probabilidades minterm para encuestas informáticas. Ejemplo 2.1.3
Solución
Deje que\(A =\) el evento de poseer una computadora de escritorio,\(B =\) el evento de tener una computadora Macintosh y\(C =\) el evento de poseer una computadora portátil. Utilizamos un mapa minterm para tres variables para ayudar a determinar patrones minterm. Por ejemplo, el evento\(AC = M_5 \bigvee M_7\) para que\(P(AC) = p(5) + p(7) = p(5, 7)\).
Los datos, expresados en términos de probabilidades minterm, son:
\(P(A) = p(4, 5, 6, 7) = 0.565\), por lo tanto\(P(A^c) = p(0, 1, 2, 3) = 0.435\)
\(P(B) = p(2, 3, 6, 7) = 0.515\), por lo tanto\(P(B^c) = p(0, 1, 4, 5) = 0.485\)
\(P(C) = p(1, 3, 5, 7) = 0.151\), por lo tanto\(P(C^c) = p(0, 2, 4, 6) = 0.849\)
\(P(ABC) = p(7) = 0.051\)\(P(AC) = p(5, 7) = 0.124\)
\(P(AB \cup AC \cup BC) = p(3, 5, 6, 7) = 0.212\)
\(P(AC) = p(5, 7) = 2p(3, 7) = 2 P(BC)\)
Utilizamos los patrones mostrados en el mapa minterm para ayudar en una solución algebraica para las diversas probabilidades minterm.
\(p(5) = p(5, 7) - p(7) = 0.124 - 0.051 = 0.073\)
\(p(1, 3) = P(A^c C) = 0.151 - 0.124 = 0.027\)\(P(AC^c) = p(4, 6) = 0.565 - 0.124 = 0.441\)
\(p(3, 7) = P(BC) = 0.124/2 = 0.062\)
\(p(3) = 0.062 - 0.051 = 0.011\)
\(p(6) = p(3, 4, 6, 7) - p(3) - p(5, 7) = 0.212 - 0.011 - 0.124 = 0.077\)
\(p(4) = P(A) - p(6) - p(5, 7) = 0.565 - 0.077 - 0.1124 = 0.364\)
\(p(1) = p(1, 3) - p(3) = 0.027 - 0.11 = 0.016\)
\(p(2) = P(B) - p(3, 7) - p(6) = 0.515 - 0.062 - 0.077 = 0.376\)
\(p(0) = P(C^c) - p(4, 6) - p(2) = 0.849 0.441 - 0.376 = 0.032\)
Se han determinado las probabilidades minterm, las cuales se muestran en el mapa minterm Figura 2.1.4. Ahora podemos calcular la probabilidad de cualquier combinación booleana de los eventos generadores\(A, B, C\). Por lo tanto,
\(P(A \cup B \cup C) = 1 - P(A^c B^c C^c) - 1 - p(0) = 0.968\)y\(P(A^c B^c C) = p(1) = 0.016\)
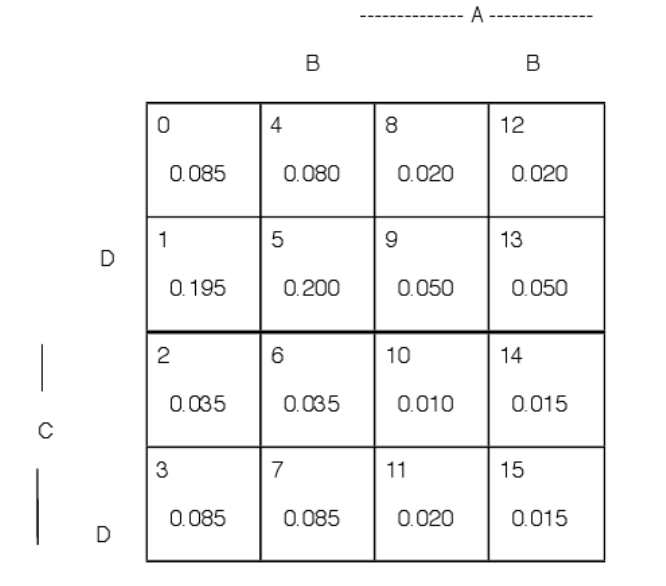
Figura 2.1.5. Probabilidades minterm para encuesta de opinión. Ejemplo 2.1.4
Ejemplo\(\PageIndex{4}\) Opinion survey
Se realiza una encuesta a 1000 personas para determinar sus opiniones sobre cuatro proposiciones. Que\(A, B, C, D\) sean los eventos que una persona seleccionada esté de acuerdo con las proposiciones respectivas. Los resultados de la encuesta muestran las siguientes probabilidades para varias combinaciones:
\(P(A) = 0.200\),\(P(B) = 0.500\),\(P(C) = 0.300\),\(P(D) = 0.700\),\(P(A(B \cup C^c) D^c) = 0.055\)
\(P(A \cup BC \cup D^c) = 0.520\),\(P(A^cBC^c D) = 0.120\),\(P(ABCD) = 0.015\),\(P(AB^c C) = 0.030\)
\(P(A^c B^c C^c D) = 0.195\),\(P(A^c BC) = 0.120\),\(P(A^c B^c D^c) = 0.120\),\(P(AC^c) = 0.140\)
\(P(ACD^c) = 0.025\),\(P(ABC^cD^c) = 0.020\)
Determinar las probabilidades para cada minterm y para cada una de las siguientes combinaciones
\(A^c (BC^c \cup B^c C)\)- es decir, no\(A\) y (\(B\)o\(C\), pero no ambos)
\(A \cup BC^c\)- es decir,\(A\) o (\(B\)y no\(C\))
Solución
Al inicio, no está claro que los datos sean consistentes o suficientes para determinar las probabilidades minterm. No obstante, un examen de los datos muestra que hay dieciséis ítems (incluyendo el hecho de que la suma de todas las probabilidades minterm es uno). Así, hay esperanza, pero ninguna garantía, de que existe una solución. Un procedimiento de eliminación por pasos, como en los ejemplos anteriores, muestra que de hecho se pueden calcular todos los minterms. Los resultados se muestran en el mapa minterm en la Figura 2.1.5. Sería deseable poder analizar el problema de manera sistemática. La formulación anterior sugiere una formulación algebraica más sistemática que debería hacer posible la solución asistida por máquina.
Formulación sistemática
El uso de un mapa minterm tiene la ventaja de visualizar la expansión minterm en relación directa con la combinación booleana. Las soluciones algebraicas de los problemas anteriores involucraron manipulaciones ad hoc de las combinaciones de probabilidad minterm de datos para encontrar la probabilidad de la combinación objetivo deseada. Se busca una formulación sistemática de los datos como un conjunto de ecuaciones algebraicas lineales con las probabilidades minterm como incógnitas, de manera que se puedan emplear métodos estándar de solución. Consideremos nuevamente la encuesta de software del Ejemplo 2.1.1.
Ejemplo\(\PageIndex{5}\) The softerware survey problem reformulated
Los datos, expresados en términos de probabilidades minterm, son:
\(P(A) = p(4, 5, 6, 7) = 0.80\)
\(P(B) = p(2, 3, 6, 7) = 0.65\)
\(P(C) = p(1, 3, 5, 7) = 0.30\)
\(P(ABC) = p(7) = 0.10\)
\(P(A^cB^c) = p(0,1) = 0.05\)
\(P(AB \cup AC \cup BC) = p(3, 5, 6, 7) = 0.65\)
\(P(AB^cC) = p(5) = 2p(3) = 2P(A^cBC)\), de manera que\(p(5) - 2p(3) = 0\)
También tenemos en cualquier caso
\(P(\Omega) = P(A \cup A^c) = p(0,1, 2, 3, 4, 5, 6, 7) = 1\)
para completar los ocho ítems de datos necesarios para determinar las ocho probabilidades minterm. El primer dato se puede expresar como una ecuación en probabilidades minterm:
\(0 \cdot p(0) + 0 \cdot p(1) + 0 \cdot p(2) + 0 \cdot p(3) + 1 \cdot p(4) + 1 \cdot p(5) + 1 \cdot p(6) + 1 \cdot p(7) = 0.80\)
Esta es una ecuación algebraica\(p(0), \cdot\cdot\cdot, p(7)\) con una matriz de coeficientes
[0 0 0 0 1 1 1 1]
Las otras pueden escribirse en consecuencia, dando ocho ecuaciones algebraicas lineales en ocho variables\(p(0)\) a través de\(p(7)\). Cada ecuación tiene una matriz o vector de coeficientes cero-uno que indica qué minterms se incluyen. Estos pueden escribirse en forma de matriz de la siguiente manera:
\(\begin{bmatrix} 1 & 1 & 1& & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 0 & & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & & -2 & 0 & 1 & 0 & 0 \end{bmatrix} \begin{bmatrix} p(0) \\ p(1) \\ p(2) \\ p(3) \\ p(4) \\ p(5) \\ p(6) \\ p(7) \end{bmatrix} = \begin{bmatrix} 1 \\ 0.80 \\ 0.65 \\ 0.30 \\ 0.10 \\0.05 \\ 0.65 \\ 0 \end{bmatrix} = \begin{bmatrix} P(\Omega) \\ P(A) \\ P(B) \\ P(C) \\ P(ABC) \\ P(A^c B^c) \\ P(AB \cup AC \cup BC) \\ P(AB^cC) - 2P(A^c BC) \end{bmatrix}\)
- Los patrones en la matriz de coeficientes están determinados por operaciones lógicas. Los obtuvimos con la ayuda de un mapa minterm.
- La solución utiliza un procedimiento algebraico, que podría llevarse a cabo de diversas maneras, incluyendo varios paquetes informáticos estándar para operaciones matriciales.
Mostramos en el módulo Minterm Vectors y MATLAB cómo podemos usar MATLAB para ambos aspectos.
Funciones de los indicadores y la expansión minterm
La discusión previa de la función indicadora muestra que la función indicadora para una combinación booleana de conjuntos es una función de valor numérico de las funciones indicadoras para los conjuntos individuales.
- Como función indicadora, toma solo los valores cero y uno.
- El valor de la función indicadora para cualquier combinación booleana debe ser constante en cada minterm. Por ejemplo, para cada ω en el minterm\(AB^cCD^c\), debemos tener\(I_A(\omega) = 1\),\(I_B(\omega) = 0\),\(I_C(\omega) = 1\), y\(I_D(\omega) = 0\). Así, cualquier función de\(I_A\),\(I_B\),\(I_C\),\(I_D\) debe ser constante sobre el minterm.
- Considere una combinación booleana\(E\) de los grupos generadores. Si\(\omega\) está en\(E \cap M_i\), entonces\(I_E(\omega) = 1\) para todos\(\omega \in M_i\), así que eso\(M_i \subset E\). Ya que cada uno\(\omega \in M_i\) o algunos\(i, E\) deben ser la unión de esos minterms que comparten una\(\omega\) con\(E\).
- \(\{M_i: i \in J_E\}\)Sea la subclase de esos minterms sobre los que\(I_E\) tiene el valor uno. Entonces
\(E = \bigvee_{J_E} M_i\)
que es la expansión a corto plazo de\(E\).


