1.10: Reflexión y transmisión en una interfaz

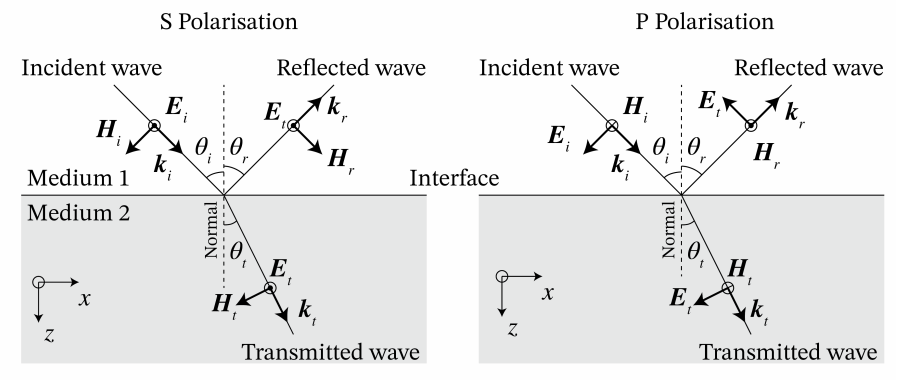
Cuando un campo electromagnético incide en una interfaz entre diferentes medios, el campo se refleja parcialmente y se transmite parcialmente. Un caso especial importante es el de una onda plana monocromática que incide en una interfaz plana como en la Figura\(\PageIndex{2}\).

Que la interfaz sea el plano\(z = 0\) entre materiales en\(z < 0\) y\(z > 0\) con permitividades\(E_i\) y\(E_t\), respectivamente. Primero asumimos que los materiales no tienen pérdidas, es decir, que las permitividades son reales. La onda plana es incidente desde el medio\(z < 0\) y el campo electromagnético incidente viene dado por:

\[ \begin{align} ε^i(r, t) &= Re [ ε^i(r)e^{−iωt}] \\[4pt] &= Re \left[ A^ie^{i(k^{i}·r−ωt)}\right] \end{align} \nonumber \]

y

\[\begin{align} H^i(r, t) &= Re [ H^i(r)e^{−iωt}] \\[4pt] &= Re \left[ \dfrac{k^i}{ωµ_{0}} × A^ie^{i(k^{i}·r−ωt)}\right] \end{align} \nonumber \]

donde k ⁱ = k ⁱ _x x + k ⁱ _{y y} + k ⁱ _{z z} z, con

\[k_{z}^i=(k_{0}^2E_{i} − (k_{x}^i)^2 − (k_{y}^i)^2)^{1/2}. \nonumber \]

Debido a que la dependencia del tiempo viene dada por\(\exp(−iωt)\) con\(ω > 0\) y la onda incidente se propaga en la dirección z positiva, se elige la raíz cuadrada positiva para k ⁱ _z. Parte del campo incidente se refleja en\(z < 0\) y parte se transmite a\(z > 0\). El campo reflejado está escrito como

\[ε^r(r, t) = Re [ ε^r(r)e^{−iωt}] = Re [ A^re^{i(k^{r}·r−ωt)}] , \nonumber \]

\[H^r(r, t) = Re [ H^r(r)e^{−iωt}] = Re [ \dfrac{k^r}{ωµ_{0}} × A^re^{i(k^{r}·r−ωt)}] , \nonumber \]

donde k ^r = k ^r _x x + k ^r _{y y} + k ^r _{z z} z, con

\[k_{z}^r=(k_{0}^2E_{i} − (k_{x}^r)^2 − (k_{y}^r)^2)^{1/2}, \nonumber \]

donde se elige el signo menos porque la onda reflejada se propaga en la dirección z negativa. El campo transmitido es para\(z > 0\)

\[ε^t(r, t) = Re [ ε^t(r)e^{−iωt}] = Re [ A^te^{i(k^{t}·r−ωt)}] , \nonumber \]

\[H^t(r, t) = Re [ H^t(r)e^{−iωt}] = Re [ \dfrac{k^t}{ωµ_{0}} × A^te^{i(k^{t}·r−ωt)}] , \nonumber \]

donde k ^t = k ^t _x x + k ^t _{y y} + k ^t _{z z} z, con

\[k_{z}^t=(k_{0}^2E_{i} − (k_{x}^t)^2 − (k_{y}^t)^2)^{1/2}. \nonumber \]

Nuestro objetivo es determinar A ^r y A ^t para A ⁱ dado.

1.9.1 Condiciones de contorno en una interfaz

Existen condiciones para la continuidad de los componentes tangencial y normal tanto de los campos eléctricos como magnéticos en una interfaz entre diferentes medios. Las condiciones de límite para los componentes tangenciales se derivan de las ecuaciones de Maxwell que contienen el operador curl-operador, es decir (1.6.2) y (1.6.3). Allí se sostiene para la interfaz z = 0 con las ondas planas incidentes, reflejadas y transmitidas introducidas anteriormente:

\[\hat{z} × (E^i + E^r ) = \hat{z} × E^t, \nonumber \]

\[\hat{z} × (H^i + H^r ) = \hat{z} × H^t, \nonumber \]

donde z es la unidad normal en la interfaz. Esto significa que los componentes tangenciales del campo eléctrico total y magnético total son continuos a través de la interfaz, o explícitamente:

\[E_{x}^i(x, y, 0) + E_{x}^r(x, y, 0) = E_{x}^t(x, y, 0), \nonumber \]

\[E_{y}^i(x, y, 0) + E_{y}^r(x, y, 0) = E_{y}^t(x, y, 0), \nonumber \]

y de manera similar para el campo magnético.

Figura\(\PageIndex{1}\): Bucle cerrado en el plano (x, z) que encierra el área A y la parte circundante de la interfaz z = 0, como se usa en la Ley de Stokes para derivar la continuidad de los componentes eléctricos y magnéticos que son tangenciales a la interfaz y paralelos al plano a través del bucle.

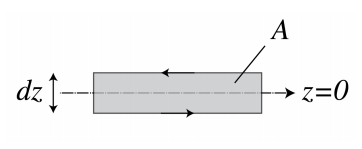
Solo demostraremos la continuidad de los componentes tangenciales para el campo eléctrico. Al elegir un bucle cerrado en el plano (x, z) que es intersectado por la interfaz z = 0 como se muestra en la Figura\(\PageIndex{1}\), e integrando el componente y de la Ley de Faraday (1.3.12) para el campo electromagnético total sobre el área A delimitada por el bucle L, obtenemos:

\[-µ_{0}\dfrac{d}{dt}\iint\limits_{A} \hat{y}H\, dA=\iint\limits_{A} \hat{y}∇ × ε\, dA=\oint\limits_{L} ε\, dl \nonumber \]

donde en el último paso utilizamos el teorema de Stokes con la dirección de integración sobre el bucle dada por la de la dirección de rotación del atornillador cuando se mueve en la dirección de la y normal. En palabras: la tasa de cambio del flujo magnético a través de la superficie A es igual a la integral del campo eléctrico tangencial sobre el bucle cerrado delimitador L.

Al tomar el límite dz → 0, la integral de superficie y las integrales sobre las partes verticales del bucle desaparecen y solo quedan las integrales del campo eléctrico tangencial sobre las partes horizontales del bucle en ambos lados de la interfaz z = 0. Dado que estas integrales son atravesadas en direcciones opuestas y las longitudes de estas partes son las mismas y arbitrarias, concluimos para el bucle como se muestra en la Figura\(\PageIndex{1}\) que

\[lim_{z↑0} ε_{x}(x, y, z, t) = lim_{z↓0} ε_{x}(x, y, z, t), \nonumber \]

donde ε es el campo eléctrico total, es decir, es igual a la suma del incidente y el campo reflejado para z < 0, and equal to the transmitted field in z > 0. Al elegir el bucle cerrado en el plano (y, z) en lugar del plano (x, z) se encuentra de manera similar que el componente y del campo eléctrico es continuo. La continuidad de los componentes tangenciales del campo magnético se deriva de manera similar.

Nuestra derivación se mantiene para campos electromagnéticos de dependencia arbitraria del tiempo. Además, la derivación utilizada anteriormente para la interfaz plana z = 0 puede generalizarse fácilmente para superficies curvas. Por lo tanto concluimos:

Los componentes tangenciales del campo eléctrico y magnético son continuos a través de cualquier interfaz.

Al integrar las ecuaciones de Maxwell que contienen el operador div-( 1.3.14), (1.3.15) sobre un pastillero con altura dz y superficies superior e inferior a ambos lados y paralelas a la interfaz, y considerando el límite dz → 0, encontramos relaciones de continuidad para los componentes normales de los campos:

\[lim_{z↑0} E_{i}\hat{z}ε_{x}(x, y, z, t) = lim_{z↓0} E_{t}\hat{z}εx(x, y, z, t), \nonumber \]

\[lim_{z↑0} H_{x}(x, y, z, t) = lim_{z↓0} H_{x}(x, y, z, t), \nonumber \]

Los componentes normales de E ε y H son continuos a través de una interfaz.

OBSERVACIÓN

Dado que todas las condiciones de contorno derivadas se mantienen para todos los tiempos t, se deduce que para los campos armónicos de tiempo también se mantienen para los campos complejos. De ahí que (\(\PageIndex{10}\)) y (\(\PageIndex{11}\)) se mantengan y de manera similar encontramos que los componentes normales de E ε y H son continuos.

1.9.2 Ley de Snell

Al sustituir los complejos campos eléctricos derivados de (\(\PageIndex{1}\)), (\(\PageIndex{4}\)) y (\(\PageIndex{7}\)) en la ecuación (\(\PageIndex{10}\)), obtenemos

\[\hat{z} × [A^ie^{i(k_{x}^{i}·x+k_{y}^{i}·y)}+A^re^{i(k_{x}^{r}·x+k_{y}^{r}·y)}]=\hat{z} × A^te^{i(k_{x}^{t}·x+k_{y}^{t}·y)}, \nonumber \]

Dado que esta ecuación debe satisfacerse para todos los puntos (x, y), se deduce que

\[k_{x}^{i}=k_{x}^{r}=k_{x}^{t}, \nonumber \]

\[k_{y}^{i}=k_{y}^{r}=k_{y}^{t}, \nonumber \]

De ahí que los componentes tangenciales de los vectores de onda de las ondas incidentes, reflejadas y transmitidas son idénticos. De hecho, si (\(\PageIndex{19}\)) no se mantendría, entonces manteniendo y fijo, las funciones exponenciales in (\(\PageIndex{18}\)) no tendrían todas la misma periodicidad que las funciones de x y entonces (\(\PageIndex{18}\)) nunca podrían satisfacerse para todos x El mismo argumento con x mantenido fijo lleva a la conclusion (\(\PageIndex{20}\)).

Sin restringir la generalidad, a partir de ahora asumiremos que el sistema de coordenadas se elige de tal manera que

\[k_{y}^{i}=k_{y}^{r}=k_{y}^{t}=0. \nonumber \]

El plano a través del vector de onda incidente y la normal a la interfaz se llama el plano de incidencia. De ahí que en el caso de (\(\PageIndex{21}\)) el plano de incidencia sea el plano (x, z).

Dado que la longitud de los vectores de onda ki y kr es k ₀ n _i, con k ₀ el número de onda en vacío y n _i = (E _i /E ₀) ^1/2 el índice de refracción, y como la longitud de kt es k ₀ n _t, con n _t = (E _t /E ₀) ^1/2, se deduce de (\(\PageIndex{19}\))

\[sin θ_{i} = \dfrac{k_{x}^{i}}{k_{0}n_{i}}=\dfrac{k_{x}^{r}}{k_{0}n_{r}}=sin θ_{r}, \nonumber \]

y

\[n_{i}sin θ_{i} = \dfrac{k_{x}^{i}}{k_{0}}=\dfrac{k_{x}^{t}}{k_{0}}=n_{t}sin θ_{t}, \nonumber \]

donde los ángulos son como en la Figura\(\PageIndex{2}\). Por lo tanto,

\[θ_{i} = θ_{r}, angle\space of\space reflection = angle\space of\space incidence, \nonumber \]

\[n_{i}sin θ_{i} =n_{t}sin θ_{t},Snell’s\space Law . \nonumber \]

La Ley de Snell implica que cuando el ángulo de incidencia θ _i aumenta, el ángulo de transmisión también aumenta. Si el medio en z < 0 es aire con índice de refracción n _i = 1 y el otro medio es vidrio con índice de refracción n _t = 1.5, entonces el ángulo máximo de transmisión ocurre cuando θ _i = 90 ^o con

\[θ_{t,max} = arcsin(n_{i}/n_{t}) = 41.8^o. \nonumber \]

Figura\(\PageIndex{2}\): Los vectores de onda incidente, reflejada y transmitida con los vectores eléctricos y magnéticos para polarización s y p. Para la polarización s, el campo eléctrico apunta fuera del plano en el instante mostrado mientras que para la polarización p el campo magnético apunta fuera del plano en el instante mostrado.

En caso de que la luz incida desde el vidrio, es decir n _i = 1.5 y n _t = 1.0, el ángulo de incidencia θ _i no puede ser mayor de 41.8 ^o porque de lo contrario no hay solución real para θ _t. Resulta que cuando θ _i > 41.8 ^o, la onda se refleja totalmente y no hay onda transmitida que se propague en el aire. Como se explica en la Sección 1.9.5, esto sin embargo no significa que no haya campo en z > 0. De hecho hay una llamada onda evanescente que no se propaga en z > 0. El ángulo θ _{i, crit} = 41.8 ^o se denomina ángulo crítico de reflexión interna total. Solo existe si una onda incide desde un medio con mayor índice de refracción sobre un medio con menor índice de refracción (n _t < n _i). El ángulo crítico es independiente de la polarización de la onda incidente.

1.9.3 Coeficientes de Fresnel

Debido a (\(\PageIndex{19}\)) y (\(\PageIndex{21}\)), escribimos k _x = k ⁱ _x = k ^r _x = k ^t _x y por lo tanto k ⁱ _z = (k ² ₀ E _i − k ² _x) ^1/2 = −k ^r _z y k ^t _z = (k ² ₀ E _t − k ² _x) ^1/2. Por lo tanto,

\[k^i = k_{x}\hat{x} + k^i_{z}\hat{z}, k^r = k_{x}\hat{x} − k^i_{z}\hat{z}, \nonumber \]

y

\[k^t =k_{x}\hat{x} − k^t_{z}\hat{z}, \nonumber \]

De acuerdo con (1.6.11), para el incidente, las ondas planas reflejadas y transmitidas deben contener:

\[A^i · k^i = A^r · k^r = A^t · k^t = 0. \nonumber \]

Elegimos una base ortonormal perpendicular a k ⁱ con vectores unitarios:

\[\hat{s}= \hat{y} , \hat{p}^i=\dfrac{1}{|k^i|}(-k_{z}^i\hat{x}+k_{x}\hat{z}), \nonumber \]

donde

\[|k^i|= (k^i · (k^i)^*)^{1/2}=(k_{x}^2 · |k_{z}^i|^2)^{1/2}, \nonumber \]

y donde al escribir el conjugado complejo anticipamos el caso el k ⁱ _z es complejo, lo que puede suceder por ejemplo cuando E _i es complejo (un caso que hasta ahora ha sido excluido pero que posteriormente se considerará) o en el caso de ondas evanescentes que se discute en la Sección 1.9.5. Tenga en cuenta que cuando k ⁱ _z es real, |k _i | = (k ² _x + (k ⁱ _z) _²) ^1/2 = k0ni. Es fácil ver que la base (\(\PageIndex{30}\)) es ortonormal en el espacio de vectores complejos bidimensionales y que s · k ⁱ = p ⁱ · k ⁱ = 0. El vector s es perpendicular al plano de incidencia, por lo tanto, el componente del campo eléctrico en esta dirección se polariza perpendicular al plano de incidencia y se denomina s-polarizado (“Senkrecht” en alemán). El otro vector base p ⁱ es (para k ⁱ real) paralelo al plano de incidencia y cuando el componente eléctrico en esta dirección se denomina p-polarizado. El vector complejo ^Ai se puede ampliar sobre esta base:

\[A^i = A^i_{s} \hat{y} + A^i_{p} \hat{p}^i. \nonumber \]

Desde

\[k^i × \hat{y} = |k^i|\hat{p}^i, k^i × \hat{p}^i =-\dfrac{k^2_{0}E_{i}}{|k^i|}\hat{y}, \nonumber \]

se deduce que el campo eléctrico y magnético de la onda plana incidente puede escribirse como

\[E^i(r) =(A^i_{s} \hat{y} + A^i_{p} \hat{p}^i)e^{ik^i·r}, \nonumber \]

\[H^i(r) = (\dfrac{|k^i|}{ωµ_{0}}A^i_{s}\hat{p}^i-\dfrac{ωE_{0}E_{i}}{|k^i|}A^i_{p}\hat{y})e^{ik^i·r}. \nonumber \]

El campo reflejado se amplía sobre la base y y p ^r con

\[\hat{p}^r=-\dfrac{1}{|k^i|}(k^i_{z}\hat{x}+k_{x}\hat{z}). \nonumber \]

El signo delante del vector unitario p ^r se elige de tal manera que su componente x sea el mismo que el de p ⁱ. Desde

\[k^r × \hat{y} = -|k^i|\hat{p}^r, k^r × \hat{p}^r =\dfrac{k^2_{0}E_{i}}{|k^i|}\hat{y}, \nonumber \]

se deduce que

\[E^r(r) =(A^r_{s} \hat{y} + A^r_{p} \hat{p}^r)e^{ik^r·r}, \nonumber \]

\[H^r(r) = (-\dfrac{|k^i|}{ωµ_{0}}A^r_{s}\hat{p}^r+\dfrac{ωE_{0}E_{i}}{|k^i|}A^r_{p}\hat{y})e^{ik^r·r}, \nonumber \]

donde usamos que k ^r · k ^r = k ₀ ² n _i ² y |k ^r | = (k _x ² + |k _z ^r | ²) ^1/2 = (k _x ² + |k _z ⁱ | ²) ^1/2 = |k ⁱ |. Para la onda plana transmitida utilizamos la base y y p ^t con

\[\hat{p}^t=\dfrac{1}{|k^t|}(-k^t_{z}\hat{x}+k_{x}\hat{z}), \nonumber \]

donde p ^t se elige de tal manera que el componente x de p ^t tenga el mismo signo que el componente x de p ⁱ. Desde

\[k^t × \hat{y} = |k^t|\hat{p}^t, k^t × \hat{p}^t =\dfrac{k^2_{0}E_{t}}{|k^t|}\hat{y}, \nonumber \]

conseguimos

\[E^t(r) =(A^t_{s} \hat{y} + A^t_{p} \hat{p}^t)e^{ik^t·r}, \nonumber \]

\[H^t(r) = (\dfrac{|k^t|}{ωµ_{0}}A^t_{s}\hat{p}^t-\dfrac{ωE_{0}E_{i}}{|k^t|}A^t_{p}\hat{y})e^{ik^t·r}, \nonumber \]

Consideramos ahora una onda plana incidente polarizada en s, es decir, A _p ⁱ = 0. Mostraremos que todas las condiciones límite pueden ser satisfechas por A _p ^r = A _p ^t = 0 y expresando apropiadamente A _s ^r y A _s ^t en términos de A _s ⁱ. Esto implica que si la onda plana incidente es polarizada en s, las ondas reflejadas y transmitidas también son polarizadas en s. Para la polarización s, el campo eléctrico tiene solo un componente y y este componente es tangencial a la interfaz z = 0. Esto lleva a la condición

\[A^i_{s}+A^r_{s}=A^t_{s}. \nonumber \]

El único componente tangencial del campo magnético es el componente x y que requiere que sea continuo para z = 0 conduce a

\[-k^i_{z}A^i_{s}+k^i_{z}A^r_{s}=-k^t_{z}A^t_{s}. \nonumber \]

Resolviendo (\(\PageIndex{44}\)), (\(\PageIndex{45}\)) para A _s ^r y A _s ^t da la siguiente fórmula para los coeficientes de reflexión y transmisión:

\[r_{s}=\dfrac{ A^r_{s} }{ A^i_{s} }=\dfrac{ k^i_{z} -k^t_{z} }{k^i_{z} +A^t_{z} }, \nonumber \]

\[t_{s}=\dfrac{ A^t_{s} }{ A^i_{s} }=\dfrac{ 2k^i_{z} }{k^i_{z} +A^t_{z} }. \nonumber \]

Solo el campo magnético tiene un componente z y es fácil verificar que H _z ⁱ + H _z ^r = H _z para z = 0.

Al observar el caso de una onda incidente polarizada p: A _s ⁱ = 0, vemos que la expresión para el campo magnético en el caso polarizado p se vuelve similar (a excepción de los signos elegidos) a la del campo eléctrico para la polarización s y a la inversa. Hacer cumplir la continuidad de los componentes tangenciales en z = 0 da para la polarización p:

\[r_{p}=\dfrac{ A^r_{p} }{ A^i_{p} }=-\dfrac{ \dfrac{k^i_{p}}{E_{i}} -\dfrac{k^t_{p}}{E_{t}}}{\dfrac{k^i_{p}}{E_{i}} +\dfrac{k^t_{p}}{E_{t}}} , \nonumber \]

\[t_{p}=\dfrac{ A^t_{p} }{ A^i_{p} }=\dfrac{ 2 \dfrac{k^i_{p}}{E_{i}} }{ \dfrac{k^i_{p}}{E_{i}} +\dfrac{k^t_{p}}{E_{t}} }. \nonumber \]

Es fácil verificar que E _z es el único componente normal y que e _i (E _z ⁱ + E _z ^r) = e _t E _z ^t para z = 0.

Los coeficientes de reflexión y transmisión r _s, r _p, t _s y tp se denominan coeficientes de Fresnel. Como se desprende de la derivación, no hay cruce entre ondas planas polarizadas s y p que inciden en una interfaz plana. Una onda plana incidente generalmente polarizada siempre se puede escribir como una combinación lineal de ondas de plano incidente polarizadas s y p. Porque en general r _s ≠ r _p y t _s ≠ t _p, se deduce que los campos reflejado y transmitido son también combinaciones lineales de campos polarizados s y p, pero con coeficientes (pesos) diferentes de estos dos estados de polarización fundamentales que para el ola incidente.

Observaciones.

1. En la derivación de los coeficientes de Fresnel no se utilizó la continuidad de los componentes normales del campo y se satisfizo automáticamente. La razón es que los campos electromagnéticos de las ondas planas fueron elegidos para ser perpendiculares a los vectores de onda. Esto implica que la divergencia de E ε y de H desaparece lo que a su vez implica que los componentes normales son automáticamente continuos a través de la interfaz.

2. Cuando kiz y ktz son ambos reales, tenemos |k ⁱ | = k ₀ n _i y |k ^t | = k ₀ n _t y los coeficientes de Fresnel pueden expresarse en los ángulos θ _i, θ _r y θ _t y los índices de refracción n _i = E _i ^1/2 /E ₀ y n _t = (E _t /E ₀) ^1/2. Debido a que k _z ⁱ = k ₀ n _{i cos θ i} y k _z ^t = k ₀ n _t cos θ _t, encontramos

\[r_{s}=\dfrac{n_{i}cosθ_{i}-n_{t}cosθ_{t}}{n_{i}cosθ_{i}+n_{t}cosθ_{t}}=-\dfrac{sin(θ_{i}-θ_{t})}{sin(θ_{i}+θ_{t})}, \nonumber \]

\[t_{s}=\dfrac{2n_{i}cosθ_{i}}{n_{i}cosθ_{i}+n_{t}cosθ_{t}}=\dfrac{2cosθ_{i}sinθ_{t}}{sin(θ_{i}+θ_{t})}, \nonumber \]

y

\[r_{p}=-\dfrac{ \dfrac{cosθ_{i}}{n_{i}}- \dfrac{cosθ_{t}}{n_{t}}}{ \dfrac{cosθ_{i}}{n_{i}}- \dfrac{cosθ_{t}}{n_{t}} }=-\dfrac{tan(θ_{i}-θ_{t})}{tan(θ_{i}+θ_{t})}, \nonumber \]

\[t_{p}=\dfrac{\dfrac{2cosθ_{i}}{n_{i}}}{ \dfrac{cosθ_{i}}{n_{i}}+ \dfrac{cosθ_{t}}{n_{t}} }=-\dfrac{ 2cosθ_{i}sinθ_{t} }{tan(θ_{i}+θ_{t})}. \nonumber \]

Para obtener las expresiones de extrema derecha en (\(\PageIndex{50}\)), (\(\PageIndex{51}\)), (\(\PageIndex{52}\)) y (\(\PageIndex{53}\)) se ha utilizado la Ley de Snell.

3. La ventaja de las expresiones (\(\PageIndex{46}\)), (\(\PageIndex{47}\)), (\(\PageIndex{48}\)), (\(\PageIndex{49}\)) en términos de los componentes del vector de onda kiz y ktz es, que también se aplican cuando k _z ⁱ y/o k _z ^t son complejas. Esto sucede por ejemplo cuando hay absorción en z < 0 or in z > 0 o ambos, o cuando E _i > E _t y el ángulo incidente está por encima del ángulo crítico, debido a que k _z ^t es puramente imaginario (ver Sección 1.9.5).

Figura\(\PageIndex{3}\): Coeficientes de reflexión y transmisión en función del ángulo de incidencia de ondas polarizadas s y p incidentes del aire al vidrio. Se indica el ángulo de Brewster θ _B.

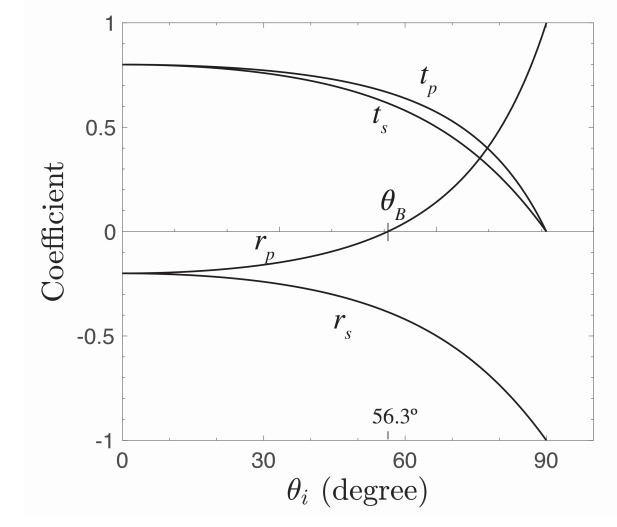
1.9.4 Propiedades de los Coeficientes de Fresnel

Para la incidencia normal: θ _i = 0, la Ley de Snell implica: θ _t = 0. Por lo tanto, (\(\PageIndex{50}\)), (\(\PageIndex{52}\)) dan:

\[r_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=\dfrac{n_{i}-n_{t}}{n_{i}+n_{t}}, \nonumber \]

Se observa que para incidencia normal r _p = r _s, como se esperaba. Obsérvese sin embargo que si no hubiéramos definido p ^_r de tal manera que su componente tangencial sea el mismo que el de p ⁱ, los dos coeficientes de reflexión tendrían el signo opuesto para la incidencia normal (como es el caso en algunos libros). Si el medio incidente es aire y el otro medio es vidrio (n _i = 1.0, n _t = 1.5), obtenemos

\[r_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=-0.2, \nonumber \]

y dado que el flujo de energía es proporcional al cuadrado del campo, se deduce que 4% de la luz incidente normal es reflejada por el vidrio. De ahí que una lente de vidrio sin recubrimiento antirreflectante refleja aproximadamente 4% de la luz en incidencia normal. El coeficiente de transmisión para la incidencia normal es:

\[t_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=\dfrac{2n_{i}}{n_{i}+n_{t}}, \nonumber \]

que para el aire-vidrio se convierte en 0.8.

OBSERVACIÓN. La conservación de energía requiere que el componente normal < Sz > del flujo de energía promediado en el tiempo a través de la interfaz sea continuo. Mediante el uso de la fórmula para el vector Poynting promediado en el tiempo de una onda plana (1.8.8), se puede verificar que los coeficientes de Fresnel son tales que el flujo de energía es efectivamente continuo.

De la Ley de Snell (\(\PageIndex{25}\)) se deduce que sin θ _t = (n _i /n _t) sin θ _i. De ahí q _t aumenta monótonamente con θ _i y por lo tanto existe alguna θ _i tal que

\[θ_{i}+θ_{t}=90^o. \nonumber \]

Para este ángulo particular de incidencia, el denominador de (\(\PageIndex{52}\)) es infinito y por lo tanto r _p = 0, es decir, la onda p-polarizada no se refleja en absoluto. Este ángulo de incidencia se denomina ángulo Brewster θ _B. Es fácil ver desde (\(\PageIndex{50}\)) que la reflexión nunca es cero para la polarización s.

Si la luz no polarizada incide en el ángulo de Brewster, la luz reflejada será puramente s-polarizada.

Dado que en el ángulo de Brewster la luz polarizada s solo se refleja parcialmente y el resto se transmite, la luz transmitida en el ángulo Brewster es una mezcla de polarización s y p. Tenemos θ _t = 90 ^o − θ _i, de ahí sin θ _t = cos θ _i y por la Ley de Snell (escribiendo θ _i = θ _B):

\[tan(θ_{B})=\dfrac{n_{t}}{n_{i}}. \nonumber \]

Vemos que siempre hay una solución, independiente de si la onda es incidente del material con el índice de refracción más pequeño o mayor. Para la interfaz aire-vidrio tenemos θ _B = 56.3 ^o y θ _t = 33.7 ^o. Por (\(\PageIndex{50}\)):

\[r_{s}(θ_{B}=56.3^o)=-0.38 \nonumber \]

de manera que (0.38) ² /2 = 0.07, o 7% de la luz no polarizada se refleja como luz puramente s-polarizada en la interfaz del vidrio de aire. Para una ola incidente de vidrio, θ _B = 33.7 ^o.

En\(\PageIndex{3}\) la Figura se muestran los coeficientes de reflexión y transmisión de las ondas polarizadas s y p en función del ángulo de incidencia para el caso de incidencia del aire al vidrio. No hay ángulo crítico de reflexión total en este caso. Se indica el ángulo Brewster. Se observa que los coeficientes de reflexión disminuyen de los valores −0.2 para θ _i = 0 ^o a -1 para θ _i = 90 ^o. Los coeficientes de transmisión disminuyen monótonamente a 0 a θ _i = 90 ^o.

La figura\(\PageIndex{3}\) muestra los coeficientes de Fresnel cuando la onda incide del vidrio al aire. El ángulo crítico es θ _{i, crit} = 41.8 ^o como se derivó anteriormente. En el ángulo de reflexión interna total los valores absolutos de los coeficientes de reflexión son idénticos a 1. De nuevo hay un ángulo donde la reflexión de la luz polarizada p es cero θ _B = 33.7 ^o.

Dependiendo de los índices de refracción y del ángulo de incidencia, los coeficientes de reflexión pueden ser negativos. El campo eléctrico reflejado tiene entonces un desplazamiento de fase π adicional en comparación con la onda incidente. En contraste, (siempre que los materiales no tengan pérdidas), el campo transmitido está siempre en fase con el campo incidente, es decir, los coeficientes de transmisión son siempre positivos.

1.9.5 Reflexión interna total y ondas evanescentes

Volvemos al caso de una ola incidente de vidrio a aire, es decir n _i = 1.5 y n _t = 1. Como se ha explicado, entonces hay un ángulo crítico, dado por sinθ _{i, crit} =n _t /n _i.

Esto es equivalente a

\[k_{x}^t=k_{0}n_{i}sinθ_{i,crit}=k_{0}n_{t} \nonumber \]

El vector de onda k ^t = k _x ^t x + k _z ^t z en z > 0 satisface:

\[(k_{x}^t)^2+(k_{z}^t)^2=k_{0}^2n_{t}^2. \nonumber \]

Debido a (\(\PageIndex{60}\)), tenemos en el ángulo crítico

\[k_{z}^t=0. \nonumber \]

Para ángulos de incidencia por encima del ángulo crítico tenemos: k _x ^t > k ₀ n _t y se deduce de (\(\PageIndex{61}\)) que (k _z ^t) ² = k ₀ ² n _t ² − (k _x ^t ) ² < 0, por lo tanto k _z ^t es imaginario:

\[k_{z}^t=±(k_{0}^2n_{t}^2-(k_{x}^t)^2)^{1/2}=±i((k_{x}^t)^2-k_{0}^2)^{1/2}, \nonumber \]

donde la última raíz cuadrada es un número real positivo. Se puede demostrar que por encima del ángulo crítico los coeficientes de reflexión son números complejos con módulo 1: |r _s | = |r _p | = 1. Esto implica que la intensidad reflejada es idéntica a la intensidad incidente, ¡mientras que al mismo tiempo los coeficientes de transmisión no son cero! Por ejemplo, para la polarización s tenemos según (\(\PageIndex{46}\)), (\(\PageIndex{47}\)):

\[t_{s}=1+r_{s}≠0, \nonumber \]

porque r _s ≠ −1 (aunque |r _s | = 1). Por lo tanto hay un campo eléctrico en z > 0, dado por

\[E(x,z)e^{-iωt}=t_{s}e^{ik_{x}^tx+ik_{z}^tz-iωt}\hat{y}=t_{s}e^{i(k_{x}^tx-ωt)}e^{-z((k_{x}^t)^2-k_{0}^2n_{t}^2)^{1/2}}\hat{y},z>0, \nonumber \]

donde hemos elegido el signo + in (\(\PageIndex{63}\)) para evitar que el campo se vuele para z → ∞. Dado que k _x ^t es real, la onda se propaga en la dirección x. En la dirección z, sin embargo, la onda no se propaga. Su amplitud disminuye exponencialmente en función de la distancia z a la interfaz y, por lo tanto, la onda se limita a una capa delgada adyacente a la interfaz. Tal onda se llama onda evanescente. Se puede calcular el vector Poynting de la onda evanescente y encontrar que este vector es paralelo a la interfaz. Por lo tanto, el flujo de energía de una onda evanescente se propaga paralelo a la interfaz, es decir, en la dirección en la que k ^t _x es positiva

Por lo tanto, no se transporta energía lejos de la interfaz hacia la región aérea. Volveremos a las ondas evanescentes en el capítulo sobre teoría de difracción.

Fuentes externas en orden recomendado

1. Video Youtube - 8.03 - Lect 18 - Índice de Refracción, Reflexión, Ecuaciones de Fresnel, Ángulo Brewster - Conferencia de Walter Lewin

2. MIT OCW - Reflection at The Air-glass Boundary: demostración de la reflexión de la luz polarizada y el ángulo Brewster.