2.4: Algunas consecuencias del principio de Fermat
- Page ID
- 129996
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Materia homogénea
En materia homogénea, el índice de refracción es constante y por lo tanto las trayectorias de OPL más cortas son líneas rectas. De ahí que en materia homogénea los rayos sean líneas rectas.
Materia no homogénea
Cuando el índice de refracción es una función de la posición como el aire con un gradiente de temperatura, los rayos se doblan hacia regiones de mayor índice de refracción, lo que lleva varios efectos bien conocidos (ver Figura\(\PageIndex{1}\)).
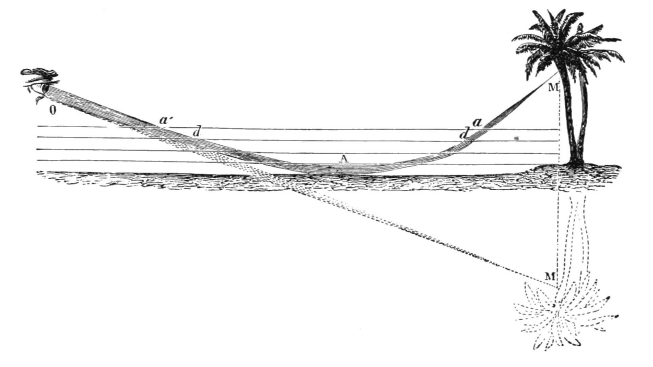
Ley de la reflexión
Considera el espejo que se muestra en la Figura\(\PageIndex{2}\) Un rayo desde el punto P puede terminar en Q de dos maneras: yendo recto de la forma P a Q o alternativamente a través del espejo. Ambas posibilidades tienen diferentes longitudes de ruta y por lo tanto diferentes tiempos de viaje y por lo tanto ambas son mínimos locales mencionados al final de la sección anterior. Consideramos aquí el camino por medio de la reflexión por el espejo. Deje que el eje x sea la intersección del espejo y el plano a través de los puntos P y Q y perpendicular al espejo. Deje que el eje y sea normal al espejo. Sea (x P, y P) y (x Q, y Q) las coordenadas de P y Q, respectivamente. Si (x, 0) es el punto donde un rayo de P a Q golpea el espejo, el tiempo de viaje de ese rayo es
\[\dfrac{n}{c}d_{1}(x)+\dfrac{n}{c}d_{2}(x)=\dfrac{n}{c}((x-x_{P})^2+y_{P}^2)^{1/2}+\dfrac{n}{c}((x_{Q}-x)^2+y_{Q}^2)^{1/2}, \nonumber \]
donde n es el índice de refracción del medio en y > 0. Según el Principio de Fermat, el punto (x, 0) debe ser tal que el tiempo de viaje sea mínimo, i.e.
\[\dfrac{d}{dx}[d_{1}(x)+d_{2}(x)]=\dfrac{x-x_{P}}{d_{1}(x)}-\dfrac{x_{Q}-x}{d_{2}(x)}=0. \nonumber \]
De ahí
\[\sin θ_{i}=\sin θ_{r}, \nonumber \]
o
\[θ_{r}=θ_{i}. \nonumber \]
donde θ i y θ r son los ángulos de incidencia y reflexión como se muestra en la Figura\(\PageIndex{2}\).
Ley de refracción de Snell
A continuación consideramos la refracción en una interfaz. Sea y = 0 la interfaz entre un medio con índice de refracción n i en y > 0 y un medio con índice de refracción n t en y < 0. Sea (x P, y P) y (x Q, y Q) con y P > 0 e y Q < 0 sean las coordenadas de dos puntos P y Q se muestran en la Figura\(\PageIndex{3}\).

¿Qué camino seguirá un rayo que va de P a Q? Dado que el índice de refracción es constante en ambos medios espacios, el rayo es una línea recta en ambos medios. Sea (x, 0) la coordenada del punto de intersección del rayo con la interfaz. Entonces el tiempo de viaje es
\[\dfrac{n_{i}}{c}d_{1}(x)+\dfrac{n_{t}}{c}d_{2}(x)=\dfrac{n_{i}}{c}((x-x_{P})^2+y_{P}^2)^{1/2}+\dfrac{n_{t}}{c}((x_{Q}-x)^2+y_{Q}^2)^{1/2}. \nonumber \]
El tiempo de viaje debe ser mínimo, de ahí que haya que mantener
\[\dfrac{d}{dx}[n_{i}d_{1}(x)+n_{t}d_{2}(x)]=n_{i}\dfrac{x-x_{P}}{d_{1}(x)}-n_{t}\dfrac{x_{Q}-x}{d_{2}(x)}=0. \nonumber \]
donde el tiempo de viaje se ha multiplicado por la velocidad de la luz en vacío. Eq. (\(\PageIndex{6}\)) implica
\[n_{i}\sin θ_{i}=n_{t} \sin θ_{t}, \nonumber \]
donde\(θ_i\) y\(θ_t\) son los ángulos entre el rayo y la normal a la superficie en el medio espacio superior y el medio espacio inferior, respectivamente (\(\PageIndex{3}\)).

De ahí que hayamos derivado la ley de la reflexión y la ley de Snell del principio de Fermat. En el Capítulo 1 la ley de reflexión y la ley de Snell se han derivado por un método diferente, a saber, de las condiciones de continuidad para los componentes del campo electromagnético en la interfaz.

