2.5: Imagen perfecta por secciones cónicas

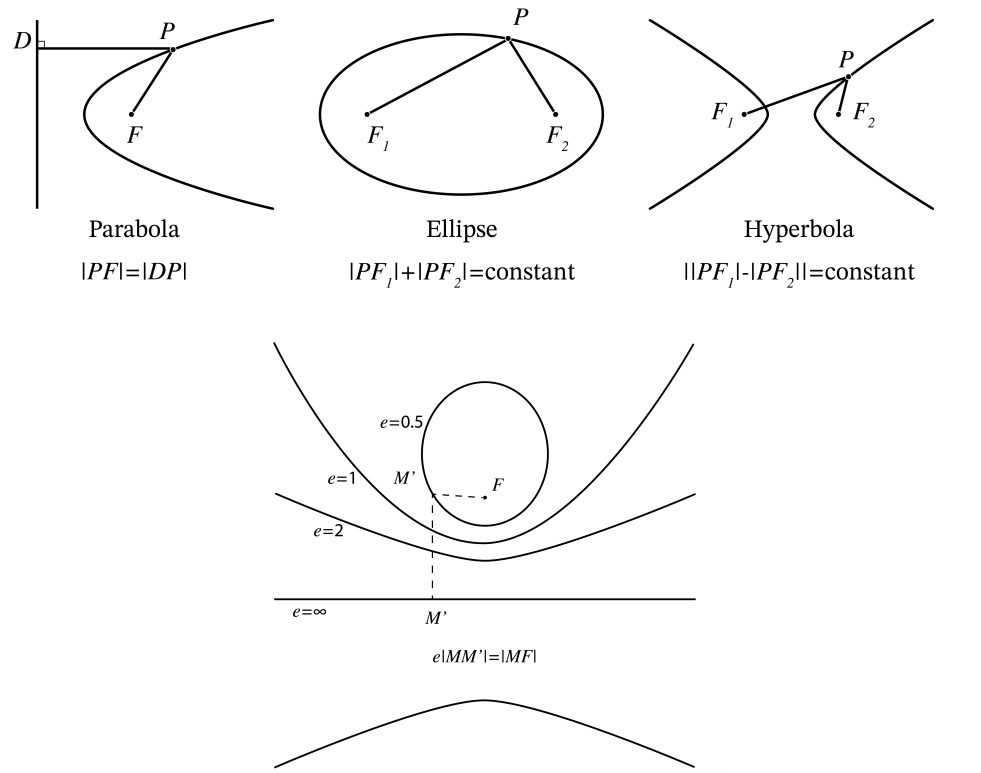
En esta sección son importantes las secciones cónicas elipse, hipérbole y parábola. En la Figura se muestran\(\PageIndex{1}\) sus definiciones como un recordatorio rápido.

Comenzamos explicando lo que en óptica geométrica se entiende por imagen perfecta. Que S sea una fuente puntual. Los rayos perpendiculares a los frentes de onda esféricos emitidos por S se ventilan radialmente desde S. Debido a objetos como lentes etc., los frentes de onda esférica se deforman y la dirección de los rayos comienza a desviarse de la dirección de propagación radial. Cuando hay un cono de rayos que viene del punto S y todos los rayos en ese cono se cruzan en el mismo punto P, entonces por principio de Fermat, todos estos rayos han atravesado caminos de mínimo tiempo de viaje. En particular, sus tiempos de viaje son iguales y por lo tanto todos suman en fase cuando llegan a P. De ahí que a P hay una alta intensidad lumínica. Si hay un cono de rayos desde el punto S que todos se cruzan en un punto P, el punto P se llama la imagen perfecta de S. Al invertir la dirección de los rayos, S es de manera similar una imagen perfecta de P. El sistema óptico en el que esto sucede se denomina estigmático para los dos puntos S y P.

Figura\(\PageIndex{1}\): Descripción general de secciones cónicas. La figura inferior muestra una definición que unifica las tres definiciones de la figura anterior introduciendo un parámetro llamado la excentricidad e. El punto F es el foco y la línea e = ∞ es la directriz de las secciones cónicas.

Figura\(\PageIndex{2}\): Imagen perfecta: un cono de rayos que divergen de S y todos se cruzan en el punto P. Los rayos continúan después de P.

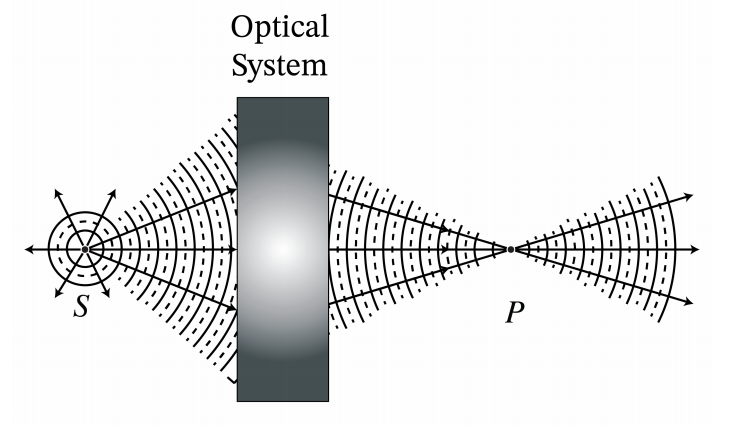
OBSERVACIÓN. El concepto de un punto de imagen perfecto existe solo en la óptica geométrica. En realidad, las aberturas finitas de lentes y otros sistemas de imagen provocan difracción debido a que los puntos de imagen nunca son perfectos sino borrosos.

Resumimos los principales ejemplos de sistemas estigmáticos.

1. Enfoque perfecto e imagen por refracción. Un haz paralelo de rayos que se propaga en un medio con índice de refracción n ₂ puede enfocarse en un punto F en un medio n ₁. Si n ₂ > n ₁, la interfaz entre los medios debe ser una hipérbole con foco F, mientras que si n ₂ < n ₁ la interfaz debe ser una elipse con foco F (ver Figs. \(\PageIndex{3}\)) y\(\PageIndex{4}\). Al invertir los rayos obtenemos una colimación perfecta. Por lo tanto, un punto S en el aire puede ser perfectamente imaginado sobre un punto F en el aire insertando un trozo de vidrio entre ellos con superficies hiperbólicas como se muestra en la Figura\(\PageIndex{4}\).
2. Enfoque perfecto de rayos paralelos por un espejo. Un haz de rayos paralelos en el aire puede enfocarse en un punto F mediante un espejo de forma parabólica con F como foco (ver Figura\(\PageIndex{5}\). Al invertir las flechas, obtenemos (dentro de la óptica geométrica) un haz perfectamente paralelo. Los espejos parabólicos se utilizan en todas partes, desde los faros de los automóviles hasta los radiotelescopios.

El resto de esta sección se puede omitir ya que las siguientes demostraciones de que la elipse, hipérbole y parábola son estigmáticas para ciertos puntos no son esenciales para la secuela. Primero supongamos que hay dos medios con índices de refracción n ₁ > n ₂ y que el punto S está al infinito en el medio con índice de refracción n ₂. Construiremos una superficie (interfaz) entre los dos medios de tal manera que todos los rayos de S se enfoquen en el mismo punto F (ver Figura\(\PageIndex{3}\) a). Debido a que S está a una distancia muy grande, los rayos que entran por la derecha son paralelos. Dado que todos los rayos paralelos han recorrido la misma distancia cuando golpean la superficie DD' perpendicular a los rayos, todos los rayos paralelos tienen la misma fase en sus puntos de intersección con el plano DD'. Si el punto A está en la interfaz buscada, el tiempo de viaje de un rayo de D a F a través de A debe ser mínimo y por lo tanto debe ser el mismo para todos los puntos A.

\[\dfrac{n_{2}}{c}|DA| +\dfrac{n_{1}}{c}|AF|=constant, \nonumber \]

donde “constante” significa el mismo valor para todos los rayos, por lo tanto, para todos los puntos A en la interfaz. Al mover el plano DD' paralelo a sí mismo, podemos lograr que para este nuevo plano DD' obtengamos:

\[e|DA|+|AF|=0, \nonumber \]

donde e = n ₂ /n ₁ < 1. De ahí que el conjunto de puntos A defina un elipsoide.

En contraste, cuando n ₂ < n ₁, como se muestra a la derecha de la Figura\(\PageIndex{3}\), entonces e < 1 y tenemos un elipsoide con F como uno de sus puntos focales.

Figura\(\PageIndex{3}\): (a) Elipsoide (n ₂ < n ₁) y (b) hiperboloide para enfocar perfectamente un haz paralelo incidente desde el medio con índice de refracción n ₂ hacia un punto en un medio con índice de refracción n ₁.

Figura\(\PageIndex{4}\): Lente con superficies hiperboloides para una imagen perfecta de un par de puntos.

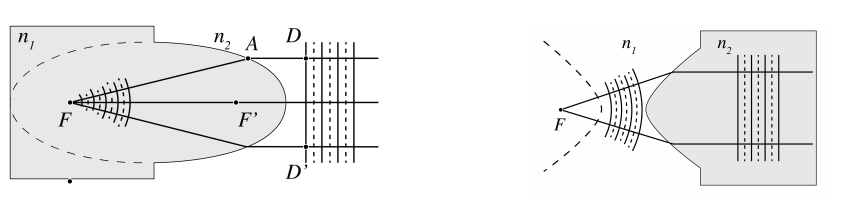
La dirección de los rayos en la Figura obviamente también\(\PageIndex{3}\) puede invertirse, en cuyo caso los rayos del punto F están todos perfectamente colimados (es decir, paralelos). Si el medio 2 consiste en vidrio y el medio 1 de aire, concluimos que al unir dos hiperboloides como se muestra en la Figura\(\PageIndex{4}\), el punto S en el aire se imagina perfectamente al punto P, también en el aire.

A continuación consideramos el enfoque perfecto de rayos paralelos por un espejo. Que haya un haz paralelo de rayos en el aire (n = 1) y supongamos que queremos enfocar todos los rayos en el punto F. Dibujamos un plano σ ₁ perpendicular a los rayos como se muestra en la Figura\(\PageIndex{5}\). Los rayos que golpearon σ ₁ han atravesado la misma longitud de trayectoria óptica. Dibujamos una segunda superficie σ ₂ paralela a σ ₁. Considera que los rayos golpean el espejo en A ₁ y A ₂. El OPL de W _j a través de A _j a F debe ser el mismo para todos los rayos:

\[OPL=|W_{1}A_{1}|+| A_{1} F|= |W_{2}A_{2}|+| A_{2} F| . \nonumber \]

Dado que σ ₂ es paralelo a σ ₁:

\[|W_{1}A_{1}|+| A_{1} D_{1}|= |W_{2}A_{2}|+| A_{2}D_{2}| \nonumber \]

De ahí que (\(\PageIndex{3}\)) se satisfaga para los puntos A para los cuales |AF| = |AD|, es decir, para los cuales la distancia a F es la misma que a σ ₂. Este es un paraboloide con F como foco y σ ₂ como directrix.

Figura\(\PageIndex{5}\): Un espejo paraboloide.

OBSERVACIÓN.

Si bien encontramos que las superficies cónicas dan una imagen perfecta para un cierto par de puntos, otros puntos no tienen imágenes perfectas en el sentido de que para un cierto cono de rayos, todos los rayos son refractados (o reflejados) al mismo punto.

Fuentes externas en orden recomendado

• KhanAcademy - Óptica Geométrica: Playlist sobre óptica geométrica elemental.
• Cursos de Yale - 16. Óptica Rayos u Geométricos I - Conferencia de Ramamurti Shankar
• Cursos de Yale - 17. Óptica Rayos u Geométricos II - Conferencia de Ramamurti Shankar