4.2: Estados de polarización y vectores Jones

Hemos visto en el Capítulo 1 que la luz es una onda electromagnética que satisface las ecuaciones de Maxwell y la ecuación de onda derivada de ellas. Dado que el campo eléctrico es un vector que oscila en cierta dirección, decimos que la onda tiene cierta polarización. En este capítulo nos fijamos en los diferentes tipos de polarización y cómo se puede manipular la polarización de un haz de luz.

Comenzamos con las ecuaciones (1.6.9) y (1.6.11) que muestran que el campo eléctrico\(\mathcal{E}(\mathbf{r}, t)\) de una onda plana siempre es perpendicular a la dirección de propagación, que es la dirección del vector de onda\(\mathrm{k}\). Dejar que la onda se propague en la\(z\) dirección -dirección:\[\mathbf{k}=\left(\begin{array}{c} 0 \\ 0 \\ k \end{array}\right) \nonumber \] Entonces el vector de campo eléctrico no tiene un\(z\) -componente y por lo tanto el campo eléctrico real en\(z\) y en el momento\(t\) puede escribirse como\[\mathcal{E}(z, t)=\left(\begin{array}{c} \mathcal{A}_{x} \cos \left(k z-\omega t+\varphi_{x}\right) \\ \mathcal{A}_{y} \cos \left(k z-\omega t+\varphi_{y}\right) \\ 0 \end{array}\right) . \nonumber \] donde \(\mathcal{A}_{x}\)y\(\mathcal{A}_{y}\) son amplitudes positivas y\(\varphi_{x}, \varphi_{y}\) son las fases de los componentes del campo eléctrico. Si bien\(k\) y\(\omega\) son fijos en este caso, podemos variar\(\mathcal{A}_{x}, \mathcal{A}_{y}, \varphi_{x}\) y\(\varphi_{y}\). Este grado de libertad es la razón por la que existen diferentes estados de polarización: el estado de polarización está determinado por la relación de las amplitudes y por la diferencia de fase\(\varphi_{y}-\varphi_{x}\) entre los dos componentes ortogonales de la onda de luz. Variar la cantidad\(\varphi_{y}-\varphi_{x}\) significa que estamos 'cambiando'\(\mathcal{E}_{y}(\mathbf{r}, t)\) con respecto a\(\mathcal{E}_{x}(\mathbf{r}, t)\). Considera el campo eléctrico en un plano fijo\(z=0\):\[\begin{aligned} \left(\begin{array}{c} \mathcal{E}_{x}(0, t) \\ \mathcal{E}_{y}(0, t) \end{array}\right) &=\left(\begin{array}{c} \mathcal{A}_{x} \cos \left(-\omega t+\varphi_{x}\right) \\ \mathcal{A}_{y} \cos \left(-\omega t+\varphi_{y}\right) \end{array}\right) \\ &=\operatorname{Re}\left\{\left(\begin{array}{c} E_{x}(0) \\ E_{y}(0) \end{array}\right) e^{-i \omega t}\right\} \\ &=\operatorname{Re}\left\{\left(\begin{array}{c} \mathcal{A}_{x} e^{i \varphi_{x}} \\ \mathcal{A}_{y} e^{i \varphi_{y}} \end{array}\right) e^{-i \omega t}\right\} . \end{aligned} \nonumber \] El vector complejo\[\mathbf{J}=\left(\begin{array}{c} E_{x}(0) \\ E_{y}(0) \end{array}\right)=\left(\begin{array}{c} \mathcal{A}_{x} e^{i \varphi_{x}} \\ \mathcal{A}_{y} e^{i \varphi_{y}} \end{array}\right) \nonumber \] se llama el vector Jones. Se utiliza para caracterizar el estado de polarización. Veamos cómo, en una posición fija en el espacio, el vector de campo eléctrico se comporta como una función del tiempo para diferentes elecciones de\(\mathcal{A}_{x}, \mathcal{A}_{y}\) y\(\varphi_{y}-\varphi_{x}\).

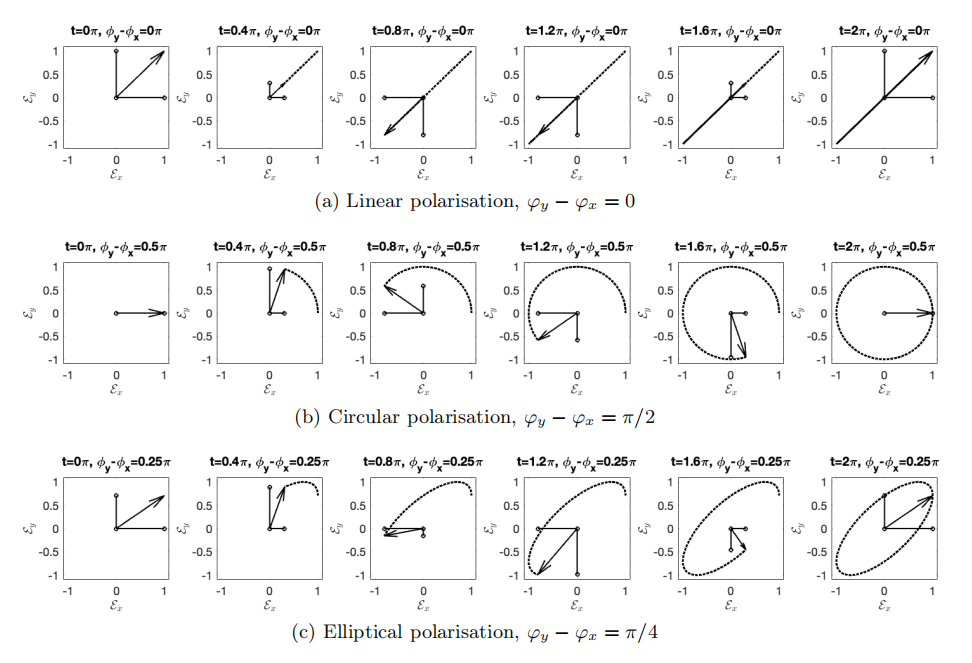
a) Polarización lineal:\(\varphi_{y}-\varphi_{x}=0\) o\(\varphi_{y}-\varphi_{x}=\pi\). Cuando\(\varphi_{y}-\varphi_{x}=0\) tenemos\[\mathbf{J}=\left(\begin{array}{c} \mathcal{A}_{x} \\ \mathcal{A}_{y} \end{array}\right) e^{i \varphi_{x}} \nonumber \] Igualdad de las fases:\(\varphi_{y}=\varphi_{x}\), significa que los componentes de campo\(\mathcal{E}_{x}(z, t)\) y\(\mathcal{E}_{y}(z, t)\) están en fase: cuando\(\mathcal{E}_{x}(z, t)\) es grande,\(\mathcal{E}_{y}(z, t)\) es grande, y cuando\(\mathcal{E}_{x}(z, t)\) es pequeño,\(\mathcal{E}_{y}(z, t)\) es pequeño. Podemos escribir\[\left(\begin{array}{l} \mathcal{E}_{x}(0, t) \\ \mathcal{E}_{y}(0, t) \end{array}\right)=\left(\begin{array}{c} \mathcal{A}_{x} \\ \mathcal{A}_{y} \end{array}\right) \cos \left(\omega t-\varphi_{x}\right), \nonumber \] lo que demuestra que para\(\varphi_{y}-\varphi_{x}=0\) el campo eléctrico simplemente oscila en una dirección dada por real el vector\(\mathcal{A}_{x} \hat{\mathbf{x}}+\mathcal{A}_{y} \hat{\mathbf{y}}\). Ver Figura\(\PageIndex{1}\) a.

Si\(\varphi_{y}-\varphi_{x}=\pi\) tenemos\[\mathbf{J}=\left(\begin{array}{c} \mathcal{A}_{x} \\ -\mathcal{A}_{y} \end{array}\right) e^{i \varphi_{x}} \nonumber \] En este caso\(\mathcal{E}_{x}(z, t)\) y\(\mathcal{E}_{y}(z, t)\) estamos desfasados y el campo eléctrico oscila en la dirección dada por el vector real\(\mathcal{A}_{x} \hat{\mathbf{x}}-\mathcal{A}_{y} \hat{\mathbf{y}}\).

b) Polarización circular:\(\varphi_{y}-\varphi_{x}=\pm \pi / 2, \mathcal{A}_{x}=\mathcal{A}_{y}\). En este caso el vector Jones es:\[\mathbf{J}=\left(\begin{array}{c} 1 \\ \pm i \end{array}\right) \mathcal{A}_{x} e^{i \varphi_{x}} \nonumber \] Los componentes del campo\(\mathcal{E}_{x}(z, t)\) y\(\mathcal{E}_{y}(z, t)\) son\(\pi / 2\) radianes (90 grados) desfasados: cuando\(\mathcal{E}_{x}(z, t)\) es grande,\(\mathcal{E}_{y}(z, t)\) es pequeño, y cuando\(\mathcal{E}_{x}(z, t)\) es pequeño, \(\mathcal{E}_{y}(z, t)\)es grande. Podemos escribir para\(z=0\) y con\(\varphi_{x}=0\):\[\begin{aligned} \left(\begin{array}{c} \mathcal{E}_{x}(0, t) \\ \mathcal{E}_{y}(0, t) \end{array}\right) &=\left(\begin{array}{c} \mathcal{A}_{x} \cos (-\omega t) \\ \mathcal{A}_{x} \cos (-\omega t \pm \pi / 2) \end{array}\right) \\ &=\mathcal{A}_{x}\left(\begin{array}{c} \cos (\omega t) \\ \pm \sin (\omega t) \end{array}\right) . \end{aligned} \nonumber \] El vector de campo eléctrico se mueve en círculo. Cuando para un observador que mira hacia la fuente, el campo eléctrico gira en sentido antihorario, la polarización se llama polarizada circularmente a la izquierda (\(+\)sign in (\(\PageIndex{9}\))), mientras que si el vector eléctrico se mueve en sentido horario, la polarización se llama derecha- polarizado circularmente (- iniciar sesión (\(\PageIndex{9}\))).

c) Polarización elíptica:\(\varphi_{y}-\varphi_{x}=\pm \pi / 2, \mathcal{A}_{x}\) y\(\mathcal{A}_{y}\) arbitraria. El vector Jones es:\[\mathbf{J}=\left(\begin{array}{c} \mathcal{A}_{x} \\ \pm i \mathcal{A}_{y} \end{array}\right) e^{i \varphi_{x}} \nonumber \] En este caso obtenemos en lugar de (\(\PageIndex{9}\)) (otra vez tomando\(\varphi_{x}=0\)): lo\[\left(\begin{array}{c} \mathcal{E}_{x}(0, t) \\ \mathcal{E}_{y}(0, t) \end{array}\right)=\left(\begin{array}{c} \mathcal{A}_{x} \cos (\omega t) \\ \pm \mathcal{A}_{y} \sin (\omega t) \end{array}\right) . \nonumber \] que demuestra que el vector eléctrico se mueve a lo largo de una elipse con ejes mayor y menor paralelos al eje\(x\) - y\(y\) -eje. Cuando el\(+\operatorname{sign}\) aplica, el campo se llama polarizado elípticamente a la izquierda, de lo contrario se denomina polarizado elípticamente a la derecha.

d) Polarización elíptica:\(\varphi_{y}-\varphi_{x}=\) cualquier otra cosa,\(\mathcal{A}_{x}\) y\(\mathcal{A}_{y}\) arbitraria. El vector Jones es ahora el más general:\[\mathbf{J}=\left(\begin{array}{c} \mathcal{A}_{x} e^{i \varphi_{x}} \\ \mathcal{A}_{y} e^{i \varphi_{y}} \end{array}\right) \nonumber \] Se puede demostrar que el vector de campo eléctrico se mueve siempre a lo largo de una elipse. La forma y orientación exactas de esta elipse, por supuesto, varía con la diferencia de fase\(\varphi_{y}-\varphi_{x}\) y la relación de la amplitud\(\mathcal{A}_{x}, \mathcal{A}_{y}\) y, excepto cuando\(\varphi_{y}-\varphi_{x}=\pm \pi / 2\), los ejes mayor y menor de la elipse no son paralelos al\(x\) - y\(y\) -eje. Ver Figura\(\PageIndex{1}\) c.

Observaciones.

1. Frecuentemente el vector Jones se normaliza de tal manera que\[\left|J_{x}\right|^{2}+\left|J_{y}\right|^{2}=1 . \nonumber \] El vector normalizado representa por supuesto el mismo estado de polarización que el no normalizado. En general, multiplicar el vector Jones por un número complejo no cambia el estado de polarización. Si multiplicamos por ejemplo por\(e^{i \theta}\), esto tiene el mismo resultado que cambiar el instante que\(t=0\), de ahí que no cambie el estado de polarización. De hecho:\[\mathcal{E}(0, t)=\operatorname{Re}\left[e^{i \theta} \mathbf{J} e^{-i \omega t}\right]=\operatorname{Re}\left[\mathbf{J} e^{-i \omega(t-\theta / \omega)}\right] \nonumber \]

2. Mostraremos en sección\(6.2\) que un campo electromagnético armónico de tiempo general, es una superposición de ondas planas con vectores de onda de la misma longitud determinados por la frecuencia de la onda pero con diferentes direcciones. Un ejemplo es el campo electromagnético cerca del plano focal de una lente. Entonces no hay una dirección particular de propagación a la que el campo eléctrico deba ser perpendicular; en otras palabras, no hay elección obvia para un plano en el que el campo eléctrico oscile en función del tiempo. Sin embargo, para cada punto del espacio existe tal plano, pero su orientación varía en general con la posición. Además, el campo eléctrico en cierto punto se mueve a lo largo de una elipse en el plano correspondiente, pero la forma de la elipse y la orientación de su eje mayor pueden ser arbitrarias. Podemos concluir que en cualquier punto de un campo electromagnético armónico de tiempo arbitrario, el vector de campo eléctrico (y de hecho también el magnético) prescribe como función del tiempo una elipse en un plano determinado que depende de la posición. En este capítulo solo consideramos el campo y el estado de polarización de una sola onda plana.

Figura\(\PageIndex{1}\): Ilustración de diferentes tipos de polarización. Arriba: polarización lineal; media: polarización circular; abajo: polarización elíptica. Las flechas horizontal y vertical indican los componentes momentáneos del campo\(\mathcal{E}_{x}, \mathcal{E}_{y} .\) La flecha gruesa indica el vector\(\mathcal{E}\). La curva negra indica la trayectoria de\(\mathcal{E}(t)\).

Fuente externa

KhanAcademy - Polarización de la luz, lineal y circular: Explicación de los diferentes estados de polarización y sus aplicaciones.