4.3: Creación y Manipulación de Estados de Polarización

Hemos visto cómo las ecuaciones de Maxwell permiten la existencia de ondas planas con muchos estados diferentes de polarización. Pero, ¿cómo podemos crear estos estados y cómo se manifiestan estos estados?

La luz natural a menudo no tiene una polarización definida. En cambio, la polarización fluctúa rápidamente con el tiempo. Para convertir dicha luz polarizada aleatoriamente en luz linealmente polarizada en cierta dirección, debemos extinguir la luz polarizada en la dirección perpendicular, de manera que la luz restante sea polarizada linealmente a lo largo de la dirección requerida. Se podría hacer esto usando la luz reflejada bajo el ángulo de Brewster (que extingue la luz polarizada p), o se podría dejar pasar la luz a través de un cristal dicroico, que es un material que absorbe la luz polarizada perpendicular a su llamado eje óptico. Un tercer método es enviar la luz a través de un polarizador de rejilla de alambre, que consiste en una rejilla metálica con hendiduras de sub-longitud de onda. Dicha rejilla solo transmite el componente de campo eléctrico que es perpendicular a las hendiduras.

Entonces supongamos que con uno de estos métodos hemos obtenido luz polarizada linealmente. Entonces surge la pregunta de cómo se puede cambiar el estado de polarización lineal en luz polarizada circular o elípticamente. O cómo se puede rotar el estado de polarización lineal sobre un cierto ángulo. Hemos visto que el estado de polarización depende de la relación de las amplitudes y de la diferencia\(\varphi_{y}-\varphi_{x}\) de fase de los componentes ortogonales\(\mathcal{E}_{y}\) y\(\mathcal{E}_{x}\) del campo eléctrico. Así, para cambiar la luz linealmente polarizada a algún otro estado de polarización, se debe introducir un cierto desplazamiento de fase (digamos\(\Delta \varphi_{x}\)) en un componente (digamos\(\mathcal{E}_{x}\)), y otro desplazamiento de fase\(\Delta \varphi_{y}\) al componente ortogonal\(\mathcal{E}_{y}\). Esto lo podemos lograr con un cristal birrefringente, como la calcita. Lo especial de tal cristal es que tiene dos índices de refracción: la luz polarizada en cierta dirección experimenta un índice de refracción de\(n_{o}\), mientras que la luz polarizada perpendicular a ella siente otro índice de refracción\(n_{e}\) (los subíndices \(o\)y\(e\) representan “ordinario” y “extraordinario”), pero para nuestro propósito no necesitamos entender esta terminología. La dirección para la que el índice de refracción es más pequeño (que puede ser cualquiera\(n_{o}\) o\(n_{e}\)) se denomina eje rápido porque su velocidad de fase es mayor, y la otra dirección es el eje lento. Debido a que hay dos índices de refracción diferentes, se pueden ver imágenes dobles a través de un cristal birrefringente. La diferencia entre los dos índices de refracción\(\Delta n=n_{e}-n_{o}\) se llama birrefringencia.

Supongamos\(n_{e}>n_{o}\) y que el eje rápido, que corresponde a\(n_{o}\) está alineado con\(\mathcal{E}_{x}\), mientras que el eje lento (que luego tiene índice de refracción\(n_{e}\)) está alineado con\(\mathcal{E}_{y}\). Si la onda recorre una distancia\(d\) a través del cristal,\(\mathcal{E}_{y}\) acumulará una fase\(\Delta \varphi_{y}=\frac{2 \pi n_{e}}{\lambda} d\), y\(\mathcal{E}_{x}\) acumulará una fase\(\Delta \varphi_{x}=\frac{2 \pi n_{o}}{\lambda} d\). Así, después de la propagación a través del cristal la diferencia de fase\(\varphi_{y}-\varphi_{x}\) ha aumentado en\[\Delta \varphi_{y}-\Delta \varphi_{x}=\frac{2 \pi}{\lambda} d\left(n_{e}-n_{o}\right) . \nonumber \]

Matrices Jones

Al dejar pasar la luz a través de cristales de diferentes espesores\(d\), podemos crear diferentes diferencias de fase entre los componentes del campo ortogonal, y de esta manera podemos crear diferentes estados de polarización. Para ser específicos, dejemos\(\mathbf{J}\), según lo dado por (4.1.4), ser el vector Jones de la onda plana antes del cristal. Entonces tenemos, para el vector Jones después del paso por el cristal:\[\tilde{\mathbf{J}}=\mathcal{M} \mathbf{J}, \nonumber \] donde\[\mathcal{M}=\left(\begin{array}{cc} e^{\frac{2 \pi i}{\lambda} d n_{o}} & 0 \\ 0 & e^{\frac{2 \pi i}{\lambda} d n_{e}} \end{array}\right)=e^{\frac{2 \pi i}{\lambda} d n_{o}}\left(\begin{array}{cc} 1 & 0 \\ 0 & e^{\frac{2 \pi i}{\lambda} d\left(n_{e}-n_{o}\right)} \end{array}\right) . \nonumber \] Una matriz como\(\mathcal{M}\), que transfiere un estado de polarización de una onda plana en otra, se llama matriz Jones. Dependiendo de la diferencia de fase que una onda acumula al viajar a través del cristal, estos dispositivos se denominan placas de cuarto de onda (diferencia de fase\(\pi / 2\)), placas de media onda (diferencia de fase\(\pi\)) o placas de onda completa (diferencia de fase\(2 \pi\)). Las aplicaciones de estas placas onduladas se discutirán en secciones posteriores.

Consideremos como ejemplo la matriz Jones que describió el cambio de luz lineal polarizada a polarización circular. Supongamos que tenemos luz polarizada diagonalmente (linealmente), de modo que\[J=\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \text {. } \nonumber \]

Queremos cambiarlo a luz polarizada circularmente, para lo\[J=\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ i \end{array}\right) \text {, } \nonumber \] cual se puede comprobar eso efectivamente\(\varphi_{y}-\varphi_{x}=\pi / 2\). Esto se puede hacer pasando la luz a través de un cristal tal que\(\mathcal{E}_{y}\) acumula una diferencia de fase de\(\pi / 2\) con respecto a\(\mathcal{E}_{x}\). La transformación mediante la cual esto se logra puede escribirse como\[\left(\begin{array}{ll} 1 & 0 \\ 0 & i \end{array}\right) \frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ 1 \end{array}\right)=\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ i \end{array}\right) . \nonumber \]

La matriz de la izquierda es la matriz Jones que describe el funcionamiento de una placa de cuarto de onda.

Otra matriz importante de Jones es la matriz de rotación. En la discusión anterior se asumió que los ejes rápido y lento estaban alineados con la dirección\(x\) - y\(y\) -dirección (es decir, eran paralelos a\(\mathcal{E}_{x}\) y\(\mathcal{E}_{y}\)). Supongamos ahora que los ejes lentos y rápidos de la placa ondulada ya no coinciden con\(\widehat{\mathbf{x}}\) y\(\widehat{\mathbf{y}}\), sino con alguna otra\(\widehat{\mathbf{x}}^{\prime}\) y\(\widehat{\mathbf{y}}^{\prime}\) como en la Figura\(\PageIndex{1}\). En ese caso aplicamos una transformación de base: el vector de campo eléctrico que se expresa en la\(\widehat{\mathbf{x}}, \widehat{\mathbf{y}}\) base debe expresarse primero en la\(\widehat{\mathbf{x}}^{\prime}, \widehat{\mathbf{y}}^{\prime}\) base antes de aplicarle la matriz Jones de la placa ondulada. Después de aplicar la matriz Jones, el campo eléctrico tiene que ser transformado de la\(\widehat{\mathbf{x}}^{\prime}, \widehat{\mathbf{y}}^{\prime}\) base a la\(\widehat{\mathbf{x}}, \widehat{\mathbf{y}}\) base.

Dejar que\(\mathbf{E}\) se den en términos de sus componentes sobre la\(\hat{\mathbf{x}}, \hat{\mathbf{y}}\) base de:\[\mathbf{E}=E_{x} \widehat{\mathbf{x}}+E_{y} \widehat{\mathbf{y}} . \nonumber \]

Para encontrar los componentes\(E_{x^{\prime}}, E_{y^{\prime}}\) sobre la\(\widehat{\mathbf{x}}^{\prime}, \widehat{\mathbf{y}}^{\prime}\) base:\[\mathbf{E}=E_{x^{\prime}} \widehat{\mathbf{x}}^{\prime}+E_{y^{\prime}} \widehat{\mathbf{y}}^{\prime} , \nonumber \] primero escribimos los vectores unitarios\(\widehat{\mathbf{x}}^{\prime}\) y\(\widehat{\mathbf{y}}^{\prime}\) en términos de la base\(\hat{\mathbf{x}}, \hat{\mathbf{y}}\) (ver Figura\(\PageIndex{1}\))\[\begin{aligned} &\widehat{\mathbf{x}}^{\prime}=\cos \theta \widehat{\mathbf{x}}+\sin \theta \widehat{\mathbf{y}}, \\ &\widehat{\mathbf{y}}^{\prime}=-\sin \theta \widehat{\mathbf{x}}+\cos \theta \widehat{\mathbf{y}}.\end{aligned} \nonumber \]

Al sustituir (\(\PageIndex{9}\)) y (\(\PageIndex{10}\)) en (\(\PageIndex{8}\)) encontramos\[\begin{aligned} \mathbf{E} &=E_{x^{\prime}} \widehat{\mathbf{x}}^{\prime}+E_{y^{\prime}} \widehat{\mathbf{y}}^{\prime} \\ &=E_{x^{\prime}}(\cos \theta \widehat{\mathbf{x}}+\sin \theta \widehat{\mathbf{y}})+E_{y^{\prime}}(-\sin \theta \widehat{\mathbf{x}}+\cos \theta \widehat{\mathbf{y}}), \\ &=\left(\cos \theta E_{x^{\prime}}-\sin \theta E_{y^{\prime}}\right) \widehat{\mathbf{x}}+\left(\sin \theta E_{x}+\cos \theta E_{y}\right) \widehat{\mathbf{y}} . \end{aligned} \nonumber \]

Comparar con (\(\PageIndex{7}\)) implica\[\left(\begin{array}{l} E_{x} \\ E_{y} \end{array}\right)=\left(\begin{array}{l} E_{x^{\prime}} \cos \theta-E_{y^{\prime}} \sin \theta \\ E_{x^{\prime}} \sin \theta+E_{y^{\prime}} \cos \theta \end{array}\right)=\mathcal{R}_{\theta}\left(\begin{array}{c} E_{x^{\prime}} \\ E_{y^{\prime}} \end{array}\right), \nonumber \] dónde\(\mathcal{R}_{\theta}\) está la matriz de rotación sobre un ángulo\(\theta\) en el sentido contrario a las agujas del reloj:\[\mathcal{R}_{\theta} \equiv\left(\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right) \nonumber \]

Eso de\(\mathcal{R}(\theta)\) hecho es una rotación sobre ángulo\(\theta\) en el sentido contrario a las agujas del reloj es fácil de ver al considerar lo que sucede cuando\(\mathcal{R}_{\theta}\) se aplica al vector\((1,0)^{T}\). Desde\(\mathcal{R}_{\theta}^{-1}=\mathcal{R}_{-\theta}\) que obtenemos:\[\left(\begin{array}{c} E_{x^{\prime}} \\ E_{y^{\prime}} \end{array}\right)=\mathcal{R}_{-\theta}\left(\begin{array}{c} E_{x} \\ E_{y} \end{array}\right) . \nonumber \]

Esta relación expresa los componentes\(E_{x^{\prime}}, E_{y^{\prime}}\) del vector Jones sobre la\(\hat{\mathbf{x}}^{\prime}, \widehat{\mathbf{y}}^{\prime}\) base, que se alinea con los ejes rápido y lento del cristal, en términos de los componentes\(E_{x}\) y\(E_{y}\) sobre la base original\(\widehat{\mathbf{x}}, \widehat{\mathbf{y}}\). Si la matriz\(\mathcal{M}\) describe la matriz Jones como se define en (\(\PageIndex{3}\)), entonces la matriz\(M_{\theta}\) para la misma placa ondulada pero con\(x^{\prime}\) eje tan lento y\(y^{\prime}\) como rápido, es, con respecto a la\(\widehat{\mathbf{x}}, \widehat{\mathbf{y}}\) base, dada por:\[\mathcal{M}_{\theta}=\mathcal{R}_{\theta} \mathcal{M} \mathcal{R}_{-\theta} . \nonumber \]

Para obtener más información sobre transformaciones de base, ver Apéndice\(F\).

Figura\(\PageIndex{1}\): Si se gira la placa ondulada, los ejes rápido y lento ya no corresponden a\(y\) y\(x\). En cambio, tenemos que introducir un nuevo sistema de coordenadas\(y^{\prime}, x^{\prime}\).

4.2.2 Polarizadores Lineales

Un polarizador que solo transmite luz polarizada horizontalmente es descrito por la matriz Jones:\[\mathcal{M}_{L P}=\left(\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right) . \nonumber \]

Claramente, la luz polarizada horizontalmente se transmite completamente, mientras que la luz polarizada verticalmente no se transmite en absoluto. De manera más general, para la luz que se polariza en ángulo\(\alpha\), obtenemos\[\mathcal{M}_{\alpha}=\mathcal{M}_{L P}\left(\begin{array}{c} \cos \alpha \\ \sin \alpha \end{array}\right)=\left(\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right)\left(\begin{array}{c} \cos \alpha \\ \sin \alpha \end{array}\right)=\left(\begin{array}{c} \cos \alpha \\ 0 \end{array}\right) \text {. } \nonumber \]

La amplitud del campo transmitido se reduce por el factor\(\cos \alpha\), lo que implica que la intensidad de la luz transmitida se reduce por el factor\(\cos ^{2} \alpha\). A esta relación se le conoce como ley de Malus.

4.2.3 Grado de Polarización

La luz natural como la luz solar no está polarizada. La polarización instantánea de la luz no polarizada fluctúa rápidamente de manera aleatoria. Un polarizador lineal produce luz lineal polarizada a partir de luz no polarizada.

La luz que es una mezcla de luz polarizada y no polarizada se llama parcialmente polarizada. El grado de polarización se define como la fracción de la intensidad total que se polariza:\[\text { degree of polarisation }=\frac{I_{p o l}}{I_{p o l}+I_{\text {unpol }}} \text {. } \nonumber \]

De (\(\PageIndex{17}\)) se deduce que la intensidad transmitida por un polarizador lineal cuando la luz no polarizada pasa incidente, es el valor promedio de\(\cos ^{2} \alpha\) a saber\(\frac{1}{2}\), multiplicado por la intensidad incidente.

4.2.4 Placas de cuarto de onda

Una placa de cuarto de onda introduce un desplazamiento de fase de\(\pi / 2\), por lo que su matriz Jones es\[\mathcal{M}_{Q W P}=\left(\begin{array}{ll} 1 & 0 \\ 0 & i \end{array}\right), \nonumber \] porque\(\exp (i \pi / 2)=i\). Para describir la transmisión real a través de la placa de cuarto de onda, la matriz debe multiplicarse por algún factor de fase global, pero debido a que solo nos importa la diferencia de fase entre los componentes de campo, este factor de fase global se puede omitir sin problema. La placa de cuarto de onda se usa típicamente para convertir la luz polarizada linealmente en luz polarizada elípticamente y viceversa. Si la luz incidente se polariza linealmente en ángulo\(\alpha\), el estado de polarización después de la placa de onda cuáter es\[\left(\begin{array}{c} \cos \alpha \\ i \sin \alpha \end{array}\right)=\left(\begin{array}{ll} 1 & 0 \\ 0 & i \end{array}\right)\left(\begin{array}{c} \cos \alpha \\ \sin \alpha \end{array}\right) \text {. } \nonumber \]

En particular, si la luz incidente es polarizada lineal bajo\(45^{\circ}\), o equivalentemente, si la placa de cuarto de onda se gira sobre este ángulo, transformará la luz polarizada linealmente en luz polarizada circularmente (y viceversa). \[\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ i \end{array}\right)=\left(\begin{array}{ll} 1 & 0 \\ 0 & i \end{array}\right) \frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \nonumber \]

Se muestra una demostración.

4.2.5 Placas de media onda

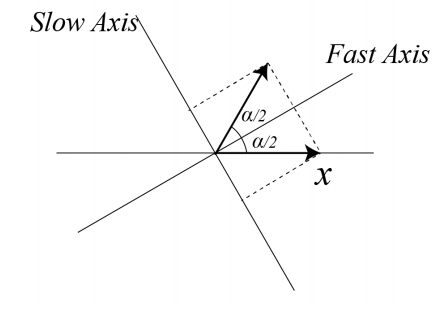
Una placa de media onda introduce un desplazamiento de fase de\(\pi\), por lo que su matriz Jones es\[\mathcal{M}_{H W P}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right), \nonumber \] porque\(\exp (i \pi)=-1\). Una aplicación importante de la placa de media onda es cambiar la orientación de la luz polarizada linealmente. Después de todo, lo que hace esta matriz es reflejar el estado de polarización en el\(x\) eje -eje. Así, si elegimos nuestro eje de espejado correctamente (es decir, si elegimos correctamente la orientación de la placa ondulada), podemos cambiar la dirección en la que la luz se polariza linealmente arbitrariamente. Se muestra una demostración en. Por poner un ejemplo: la polarización de una onda que es paralela a la\(x\) dirección -se puede girar sobre ángulo\(\alpha\) girando el cristal de tal manera que el eje lento hace ángulo\(\alpha / 2\) con el\(x\) eje -eje. Al propagarse a través del cristal, el eje rápido obtiene una fase adicional de\(\pi\), debido a lo cual el vector eléctrico hace ángulo\(\alpha\) con el\(x\) eje -eje (ver Figura\(\PageIndex{2}\)).

Figura\(\PageIndex{2}\): Rotación de la luz polarizada horizontalmente sobre un ángulo\(\alpha\) utilizando una placa de media onda.

4.2.6 Placas de onda completa

Una placa de onda completa introduce una diferencia de fase de\(2 \pi\), que es lo mismo que introducir ninguna diferencia de fase entre los dos componentes de campo. Entonces, ¿qué puede ser posiblemente una aplicación para una placa de onda completa? Necesitamos recordar de la ecuación ((\(\PageIndex{1}\))) que la diferencia de fase es\(2 \pi\) solo para una longitud de onda particular. Si enviamos a través de luz polarizada linealmente (digamos verticalmente) de otras longitudes de onda, éstas se polarizarán elípticamente, mientras que la luz con la longitud de onda correcta\(\lambda_{0}\) permanecerá polarizada verticalmente. Si entonces dejamos que toda la luz pase a través de un polarizador horizontal, la luz con longitud de onda\(\lambda_{0}\) quedará completamente apagada, mientras que la luz de otras longitudes de onda podrá pasar por lo menos parcialmente. Por lo tanto, las placas de onda completa se pueden usar para filtrar longitudes de onda específicas de la luz.