1.3: Refracción en una superficie plana

Cuando un rayo de luz entra en un medio más denso se refracta hacia la normal de tal manera que la relación del seno del ángulo de incidencia al seno del ángulo de refracción es constante, denominándose a esta constante el índice de refracción \(n\).

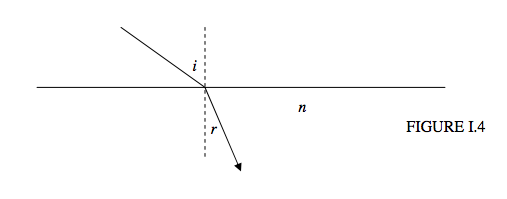
Esto está bien hasta donde va, pero tal vez podamos hacerlo mejor.

1. Recuerda al profesor cascarraca que te dará solo medias notas a menos que también digas que el rayo incidente, el rayo refractado y lo normal son coplanares.
2. La ecuación

\[ \dfrac{ \sin i }{ \sin r } = n, \label{eq:1.3.1} \]

donde\(n\) está el índice de refracción del medio, está bien siempre y cuando la luz entre al medio desde un vacío. El índice de refracción del aire es muy poco diferente de la unidad. Los detalles sobre el índice de refracción del aire pueden encontrarse en la Sección 7.1 de Atmósferas Estelares y la Sección 11.3.3 de Mecánica Celestial. Si la luz se mueve de un medio a otro, la ley de la refracción toma la forma

\[ n_1 \sin \theta_1 = n_2 \sin \theta_2. \label{eq:1.3.2} \]

iii. El enunciado de la ley de Snell como se ha dado anteriormente implica, si se toma literalmente, que existe una relación uno a uno entre el índice de refracción y la densidad. Debe haber una fórmula que relacione el índice de refracción y la densidad. Si te digo la densidad, deberías poder decirme el índice de refracción. Y si te digo el índice de refracción, deberías poder decirme la densidad. Si arregla las sustancias en orden de densidad creciente, este también será su orden de aumentar el índice de refracción.

No del todo cierto

Esto no es del todo cierto, y, si pasas un poco de tiempo buscando densidades e índices de refracción de sustancias en, por ejemplo, el Manual de Física y Química CRC, encontrarás muchos ejemplos de sustancias menos densas que tienen un índice de refracción más alto que las sustancias más densas. Es cierto en sentido general generalmente que las sustancias más densas tienen índices más altos, pero no hay correspondencia uno a uno.

De hecho, la luz se dobla hacia lo normal en un medio “más denso” como resultado de su velocidad más lenta en ese medio, y de hecho la velocidad\(v\) de la luz en un medio de índice de refracción\(n\) viene dada por

\[ n = c/v, \label{eq:1.3.3} \]

donde\(c\) esta la velocidad de la luz al vacio. Ahora la velocidad de la luz en un medio es función de la permitividad eléctrica\( \epsilon \) y la permeabilidad magnética\( \mu \):

\[ v = 1 / \sqrt{ \epsilon \mu }. \label{eq:1.3.4} \]

La permeabilidad de la mayoría de los medios no ferromagnéticos es muy poco diferente de la de un vacío, por lo que el índice de refracción de un medio está dado aproximadamente por

\[ n \approx \sqrt{ \frac{ \epsilon }{ \epsilon_0 }} \label{eq:1.3.5} \]

Así, existe una correlación mucho más estrecha entre el índice de refracción y la permitividad relativa (constante dieléctrica) que entre el índice de refracción y la densidad. Obsérvese, sin embargo, que ésta es sólo una relación aproximada. En la teoría detallada hay una pequeña dependencia de la velocidad de la luz y de ahí el índice de refracción de la frecuencia (de ahí la longitud de onda) de la luz. Así, el índice de refracción es mayor para la luz violeta que para la luz roja (la luz violeta se refracta más violentamente). La división de la luz blanca en sus colores constituyentes por refracción se llama dispersión.

Aquí hay un rayo de luz viajando de un medio a otro:

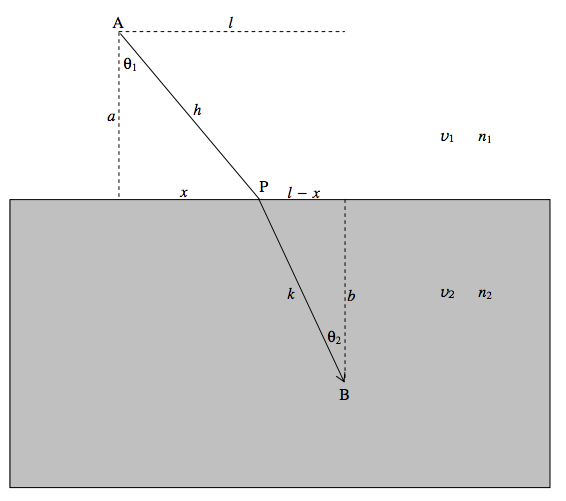
Se mueve más rápido en el medio superior que en el medio inferior.

Tiempo necesario para llegar de A a B:

\[ t = \frac{ \sqrt{ a^2 + x^2}}{ v_1} + \frac{ \sqrt{ b^2+(1-x)^2 }}{v^2}. \label{eq:1.3.6} \]

Es decir:

\[ ct = n_1 \sqrt{ a^2 + x^2 } + n_2 \sqrt{ b^2 + (l -x)^2}. \label{eq:1.3.7} \]

Aquí está el tiempo tomado en función de la posición de P, calculado para\(n_2 / n_1 = 1.5\).

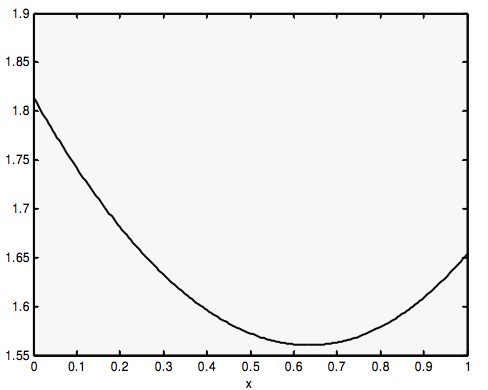
Como ve, pasa por un mínimo. Puedes encontrar dónde está diferenciando Ecuación\( \ref{eq:1.3.7}\):

\[ c \frac{ dt }{ dx } = \frac{ n_1x }{ \sqrt{ a^2 + x^2 }} - \frac{ n_2 ( l - x ) }{ \sqrt{ b^2 + ( l -x )^2 }} = n_1 \sin \theta_1 - n_2 \sin \theta_2, \label{eq:1.3.8} \]

Esto es cero cuando\( n_1 \sin \theta_1 − n_2 \sin \theta_2 = 0 \). Así la ley de Snell es tal que el camino realmente tomado es el camino que toma el menor tiempo. ¿Trivial, o profundo?

Construcción de Huygens

Aquí hay un frente de onda que se mueve hacia arriba. Los “rayos” de luz son normales al frente de onda.

La construcción de Huygens es una forma de predecir lo que sucederá a continuación. Dice que se puede imaginar que cada punto del frente de onda sea una fuente que genere un poco de ondícula. Entonces, después de un poco de tiempo las ondículas se ven así, y el nuevo frente de onda es la tangente común a todas las ondículas.

Esto puede sonar trivial al principio, aunque se ha escrito mucho al respecto, es decir, si representa la realidad, o es meramente una construcción conveniente. Y, si es real, ¿qué pasa con las ondículas en la dirección hacia atrás? No vamos a perseguir eso aquí, pero podemos usar la construcción Huygens como una forma interesante de pensar sobre la ley de Snell.

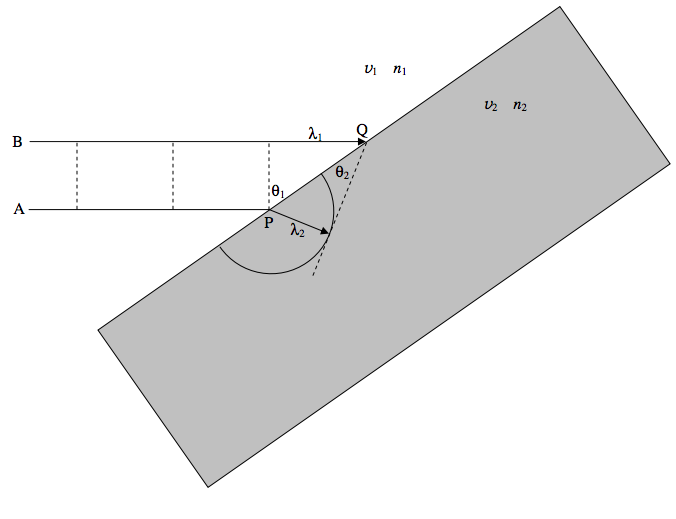
Un haz de luz de longitud de onda\( \lambda_1 \) se acerca a un bloque de vidrio desde la izquierda a velocidad\( v_1 \). Las líneas discontinuas representan los frentes de onda. El rayo A llega primero al bloque, en P. Se genera una ondícula a P, moviéndose con velocidad\( v_2 \). El dibujo se realiza para el instante en que el rayo B alcanza el punto Q. El nuevo frente de onda es la tangente de Q a la pequeña ondícula que comenzó en P. La geometría lo mostrará\( \frac{ \lambda_1 } { \lambda_2 } = \frac{ v_1 }{ v_2 } = \frac{ n_2 }{ n_1} \) y por lo tanto\( \sin \theta_1 = n_2 \sin \theta_2 \).

Ejemplo\(\PageIndex{1}\): Refraction through a glass block

La Figura I.6 muestra un rayo de luz que pasa a través de un bloque de vidrio rectangular de espesor\( t\) e índice de refracción\( n \) (tomado como 1.5 en el dibujo). La normal a la superficie del bloque forma un ángulo\( \theta \) con el rayo entrante. Es cuestión de geometría simple (¡hazlo!) para mostrar que el desplazamiento lateral\( h \) del rayo viene dado por

\[ h = t ( \sin \theta - \cos \theta \tan \phi ), \label{eq:1.3.6.1} \]

donde\( \phi \) está el ángulo de refracción, dado por\( \sin \theta = n \sin \phi \). En términos de\( \theta, n\) y\( t \), esto es

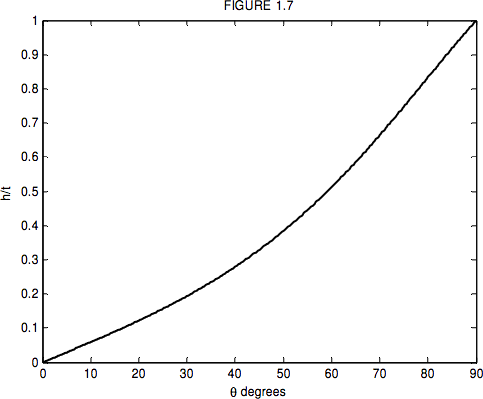
\[ h = t \sin \theta \left( 1 - \frac{ \cos \theta }{ \sqrt{ n^2 - \sin^2 \theta }}\right). \label{eq:1.3.7.1} \]

La figura I.7 se dibuja para\( n = 1.5 \).

Uno podría imaginarse haciendo uso de esto para medir la distancia entre dos puntos cercanos entre sí. Por ejemplo supongamos que tienes una fotografía de algunas estrellas en una placa fotográfica antigua, e incluye un par cercano de estrellas, y quieres medir la distancia entre las dos imágenes estelares. (Hoy la fotografía estaría en un detector CCD, y la distancia entre las dos imágenes se grabaría electrónicamente, razón por la cual especifico una placa fotográfica antigua.) Miras la fotografía a través de un microscopio y ves una de las estrellas bisectadas por una mira en el ocular del microscopio. Pero tienes una placa de vidrio frente a la fotografía, e inclinas la placa para desplazar las imágenes para que las imágenes se muevan y ahora la segunda estrella esté bisectada por el punto de mira. Desde el gran ángulo a través del cual inclinas la placa puedes calcular la pequeña distancia entre las dos imágenes. Querrás usar luz monocromática, y necesitarás conocer el índice de refracción a esa longitud de onda.

¿Cómo va a medir el ángulo a través del cual ha girado la placa? Bueno, podrías hacer brillar un rayo láser de él; la luz reflejada se moverá al doble de la velocidad de la placa, y podrías dejar que ilumine una hoja de papel cuadriculado a varios pies de distancia. Así, la diminuta distancia entre las imágenes corresponderá a una gran distancia en el papel cuadriculado. Puede haber uno o dos detalles prácticos más en los que te gustaría pensar. Por ejemplo, ¿qué tan gruesa querrías que fuera la placa de vidrio? ¿Un portaobjetos de microscopio delgado, tal vez, o algo mucho más grueso que eso? ¿Sería mejor trabajar en ángulos\( \theta \) menores a unos 40º donde la pendiente de la Figura I.7 es pequeña, o en ángulos mayores a 50º donde la pendiente es mayor?

También es posible que desee mover un rayo láser lateralmente a través de una cantidad pequeña y controlada. Se podría poner un bloque de vidrio en un plato giratorio que podría girarse a través de un pequeño ángulo medible y así mover el rayo láser lateralmente y con precisión a través de una cantidad muy pequeña.

Sigamos con el bloque de vidrio.

Ejemplo\(\PageIndex{2}\): Refraction through a moving glass block

Demostrar que, si el bloque de vidrio se girara en sentido antihorario con velocidad angular\( \omega \), el rayo láser se movería hacia arriba a una velocidad

\[ \dot{h} = t \left[ \cos \theta - \frac{ n^2 - 2n^2 \sin^2 \theta + \sin^4 \theta }{ ( n^2 - \sin^2 \theta )^{3/2} }\right]\omega \label{eq:1.3.8.1} \]

Si escribimos\( \sin^2 \theta \) como\( 1 - \cos^2 \theta \), podremos expresarlo íntegramente en términos de\( \cos \theta \). Y si, con fines ilustrativos, tomo\( n = 1.5 \), la ecuación se vuelve

\[ \frac{ \dot{h}}{ t \omega } = c + \frac{ 1.25 - 2.5c^2 - c^4 }{ (1.25 + c^2 ) ^ {3/2}}, \label{eq:1.3.9} \]

donde\( c = \cos \theta \). Para facilitar el cómputo, voy a establecer\( C = c^2 \). Ecuación\( \ref{eq:1.3.9} \) entonces se convierte

\[ \frac{ \dot{h}}{ t \omega } = c + \frac{ 1.25 - C(2.5+C)}{ (1.25 +C ) ^ {3/2}}. \label{eq:1.4.0} \]

Esto es fácil de calcular, y el resultado se muestra en la gráfica a continuación.

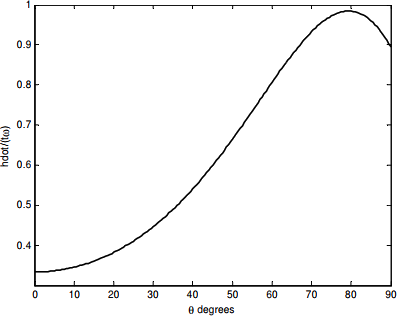
Vemos, quizás para nuestra sorpresa, que\( \dot{h} \) & pasa por un máximo a aproximadamente\( \theta \) = 79º. Para obtener la Ecuación\( \ref{eq:1.3.9} \), tuvimos que diferenciar Ecuación\( \ref{eq:1.3.7}\). Ahora, para saber dónde\( \dot{h} \) pasa por un máximo, vamos a tener que diferenciarnos de nuevo, aunque misericordiosamente podemos diferenciar Ecuación\( \ref{eq:1.4.0} \) con respecto a\( C \) más que a\( \theta \). Si hacemos esto, y luego ponemos la derivada a cero, encontramos, después de alguna simplificación,

\[\frac{ 1 }{ 2C^{1/2 }} = \frac{ 5 + 1.25C + 0.5C^2 }{ (1.25 + C)^{5/2}} \label{eq:1.4.1} \]

Si cuadramos esto y recolectamos poderes de\( C \), llegamos a una ecuación cuártica en\( C \):

\( 625 - 17980C - 6240C^2 - 2176C^3 + 256C^4 = 0. \)

donde\( C = c^2 = \cos^2 \theta\).

La solución a esta ecuación es\( C = 0.034 346 549 0\), correspondiente a

\( \theta \)= 79º.319 731 1