1.6: Refracción por un prisma

La Figura I.11 muestra un prisma isósceles de ángulo\(\alpha\) y un rayo de luz que pasa a través del mismo.

He dibujado sólo un rayo de un solo color. Para la luz blanca, los colores se dispersarán, siendo la luz violeta desviada por el prisma más que la luz roja. Escogeremos una longitud de onda tal que el índice de refracción del prisma sea\(n\). La desviación D de la luz desde su dirección original es\(\theta_1 − \phi_1 + \theta_2 − \phi_2\). Quiero imaginarme, ahora, si mantenemos fijo el rayo incidente y giramos el prisma, ¿cómo varía la desviación con el ángulo de incidencia\(\theta_1\)? Por geometría,\(\phi_2 = \alpha − \phi_1\), para que la desviación sea

\[ D = \theta_1 + \theta_2 -\alpha.\label{eq:1.6.1} \]

Aplicar la ley de Snell en cada una de las dos superficies refractantes:

\[ \frac{\sin\theta_1}{\sin\phi_1} =n \quad \text{and} \quad \frac{\sin\theta_2}{\sin(\alpha - \phi_1)}=n, \label{eq:1.6.2a,b} \]

y eliminar\(\phi_1\):

\[ \sin\theta_2 = \sin\alpha\sqrt{n^2-\sin^2\theta_1} -\cos\alpha\sin\theta_1. \label{eq:1.6.3} \]

Ecuaciones\(\ref{eq:1.6.1}\) y nos\(\ref{eq:1.6.3}\) permiten calcular la desviación en función del ángulo de incidencia\(\theta_1\). La desviación es menor cuando la luz atraviesa el prisma simétricamente\(\theta_1 = \theta_2\), siendo la luz dentro del prisma luego paralela a la base. Poner\(\theta_1 = \theta_2\) en ecuación muestra que se produce una desviación mínima para un ángulo de incidencia dado por

\[ \sin \theta _ { 1 } = \frac { n \sin \alpha } { \sqrt { 2 ( 1 + \cos \alpha ) } } = n \sin \frac { 1 } { 2 } \alpha. \label{eq:1.6.4} \]

El ángulo de desviación mínima\(D_{\text{min}}\) es\(2\theta_1 − \alpha\), donde\(\theta_1\) viene dado por Ecuación\(\ref{eq:1.6.4}\), y esto conduce a la siguiente relación entre el índice de refracción y el ángulo de desviación mínima:

\[ n = \frac{\sin\frac{1}{2}(D_{\text{min}}+\alpha)}{\sin\frac{1}{2}\alpha}.\label{eq:1.6.5} \]

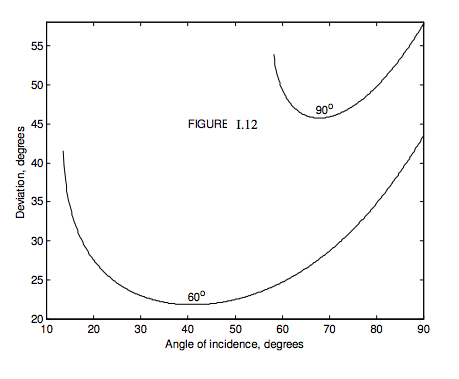
De particular interés son los prismas con\(\alpha\) = 60 ° y\(\alpha\) = 90 °. He dibujado, en la Figura I.12 la desviación versus ángulo de incidencia para prismas de 60 y 90 grados, utilizando (por razones explicaré)\(n = 1.31\), que es aproximadamente el índice de refracción del hielo. Para el prisma de hielo de 60 °, el ángulo de desviación mínima es de 21 ° .8, y para el prisma de hielo de 90 ° es de 45 ° .7.

Figura I.12:

Halo Solar

Cuando los cristales hexagonales de hielo están presentes en la atmósfera, la luz solar se dispersa en todas las direcciones, de acuerdo con los ángulos de incidencia en los diversos cristales de hielo (que pueden o no estar orientados aleatoriamente). Sin embargo, la tasa de cambio de la desviación con ángulo de incidencia es menos cercana a la desviación mínima; en consecuencia, mucha más luz se desvía en 21 ° .8 que a través de otros ángulos. En consecuencia vemos un halo de radio de unos 22 ° alrededor del Sol.

Visto de lado, un cristal hexagonal es rectangular y, en consecuencia, la refracción es como a través de un prisma de 90º (Figura I.14):

Nuevamente, la tasa de cambio de desviación con ángulo de incidencia es menos cercana a la desviación mínima, y en consecuencia podemos ver otro halo, de radio alrededor de 46°. Para ambos halos, el violeta se desvía más que el rojo, y por lo tanto ambos halos se tiñen de violeta por fuera y de rojo en el interior.

Figura: Halos solares con un halo mayor y más tenue de 46° y un halo de 22° con un arco tangente superior. (CC BY 2.0; Fototeca NOAA).