7.1.1: Justificación- anisotropía natural e inducida

Para medios isótropos supusimos la existencia de una fuerza recuperadora a nivel molecular proporcional a la separación entre cargas

\[
\mathbf{F}_{\text {int }}=m \omega_{0}^{2} \mathbf{r} \notag
\]

Ya dijimos que la linealidad no implicaba que \(\omega_{0}\) fuese un escalar. De hecho, sólo será un escalar si la dirección en que produzcamos la separación de cargas es indiferente, esto es, si los efectos de un campo eléctrico aplicado son igualmente eficaces separando cargas independientemente de su dirección. Si ocurre así, según la deducción que hicimos, \(\epsilon_{0} \chi_{e}\) será también un escalar en la expresión \(\mathbf{P}=\epsilon_{0} \chi_{e} \mathbf{E}, \quad \mathrm{y} \quad \mathbf{F} \| \mathbf{r}\) implicará naturalmente \(\mathbf{P} \| \mathbf{E}\).

Imaginemos ahora el caso de una molécula biatómica. Vemos claramente que hay una dirección intrínsecamente privilegiada en un material cuya estructura microscópica es de este tipo (figura 7.1, b). Un mismo campo será más eficaz deformando la nube electrónica en una dirección que en otra.

Figura \(\PageIndex{1}\): Significado microscópico de la isotropía. a) la perturbación originada por un campo sobre un átomo es igualmente eficaz en todas las direcciones (isotropía microscópica). b) la perturbación sobre una molécula diatómica es más eficaz en unas direcciones que en otras (anisotropía microscópica).

Figura \(\PageIndex{2}\): Diferentes modos de inducir la anisotropía en un material. a) efecto electroóptico b) magnetoóptico c) fotoelástico.

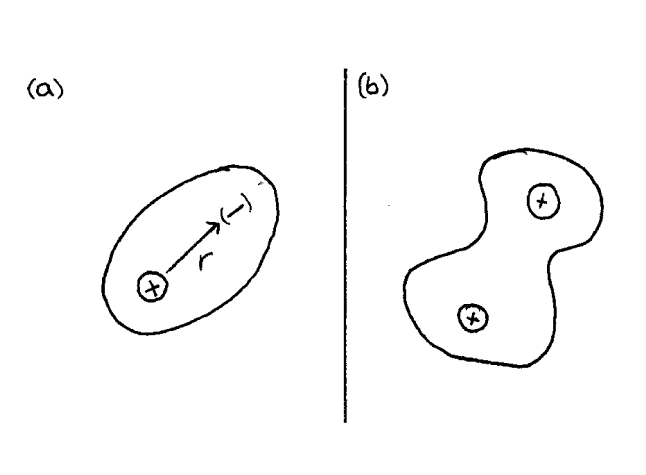
Ahora se cumplen las siguientes relaciones, donde el gorro denota una matriz (que introduce la dependencia de la dirección).

\[
\begin{aligned}
\mathbf{F}_{i n t} &=\hat{M} \mathbf{r} \\
\mathbf{P} &=\hat{\chi}_{e} \epsilon_{0} \mathbf{E} \\
\mathbf{D} &=\epsilon_{0}\left(\hat{1}+\hat{\chi}_{e}\right) \mathbf{E}=\hat{\epsilon} \mathbf{E}
\end{aligned}
\]

los parámetros \(\hat{M}, \hat{\chi}_{e}\) y \(\hat{\epsilon}\) tienen ahora carácter tensorial \({ }^{1}\). Como consecuencia de ello, los índices de refracción dependerán del estado de polarización (dirección del campo). Nos llevará un cierto tiempo (y muchos cálculos) cuantificar esta dependencia.

Imaginemos un medio hecho de moléculas anisótropas como las de la figura \(\PageIndex{1}\), (b). Si están distribuídas de modo aleatorio, los promedios espaciales harán que el medio sea macroscópicamente isótropo (pej, el aire). Para obtener medios macroscópicamente anisótropos debemos pensar en configuraciones más rígidas (que mantengan las moléculas orientadas en la misma dirección). Es decir, líquidos, pero, sobre todo, sólidos cristalinos.

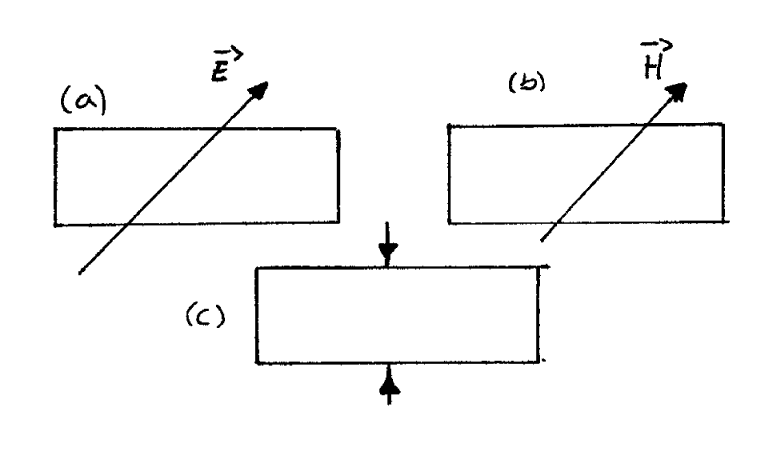
La anisotropía de los cristales podríamos llamarla de origen natural. Pero nosotros podemos crear anisotropías inducidas. Por ejemplo, si aplicamos un fuerte campo eléctrico estacionario a ciertos medios, los convertiremos en anisótropos por alineación de momentos dipolares eléctricos. Lo mismo si se trata de un campo magnético estacionario. Pero también podemos causar anisotropía por medios mecánicos, como presiones o estiramientos (figura \(\(\PageIndex{2}\)\), c). En conclusión, la anisotropía se puede controlar a voluntad (siempre que no haya histéresis), por variados medios.

_{_________________________________________________________________}

^{1. Omitiremos en lo que sigue la distinción notacional entre la matriz identidad, \(\hat{1}\) y el escalar \(1 .\) - medios homogéneos.}