9.2: Coherencia

Si tomamos ondas escalares armónicas

\[
\begin{aligned}
&E_{1}=A_{1}(\mathbf{r}) \cos \left(\omega_{1} t-g_{1}(\mathbf{r})\right) \\
&E_{2}=A_{2}(\mathbf{r}) \cos \left(\omega_{2} t-g_{2}(\mathbf{r})\right)
\end{aligned}
\]

y hacemos el promedio temporal

\[
I \propto\left\langle E^{2}\right\rangle=\frac{A_{1}^{2}}{2}+\frac{A_{2}^{2}}{2}+A_{1} A_{2}\left\langle\cos \left(\left(\omega_{1}-\omega_{2}\right) t+g_{2}-g_{1}\right)\right\rangle \notag
\]

dicho de otra forma

\[
I=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}}\left\langle\cos \left(\left(\omega_{1}-\omega_{2}\right) t+g_{2}-g_{1}\right)\right\rangle \notag
\]

El término interferencial depende más lentamente del tiempo cuanto más próximas entre sí estén las frecuencias. El problema es que las resoluciones temporales en laboratorio son muy toscas: para que el ti varíe tan lentamente como para que pueda verse en laboratorio, ambas frecuencias deben ser muy parecidas (como una parte en \(10^{11}\) ). En resumen,: si \(\omega_{1} \not \omega_{2}\) el promedio temporal del término interferencial será nulo a efectos de observación. A partir de ahora nos quedaremos con el caso óptimo: interferencias no dependientes del tiempo, es decir, \(\omega_{1}=\omega_{2}\). Esto garantiza la estabilidad en el tiempo del fenómeno de interferencia.

El fenómeno de interferencia es muy sensible; tanto que nos obliga a revisar el proceso de emisión de luz monocromática. La luz monocromática se puede obtener por transiciones atómicas de un gas muy enrarecido y enfriado. En concreto, podemos pensar que tenemos dos fuentes, por ejemplo, dos átomos idénticos excitados por una colisión electrónica. Estos átomos sólo emitirán luz hasta que decaigan al estado fundamental. Como hemos visto cuando estudiamos el modelo clásico de la radiación, este tiempo depende del término de rozamiento \(\gamma\). El átomo decae exponencialmente al estado fundamental en tiempos del ns.

Figura \(\PageIndex{1}\): Proceso de emisión atómica continuamente estimulada. Se producen saltos de fase y amplitud cada \(\delta t=10^{-10} \mathrm{~s}\)

De modo que tenemos dos ondas, cada una de las cuales dura del orden de un \(n s\). Eso es demasiado breve para poder observarlo. Para tener una emisión continuada necesitamos reexcitar periódicamente al átomo. El problema que surge es que en esas colisiones es imposible predecir en qué estado interno quedará el átomo. Con ocasión de cada colisión el campo eléctrico emitido cambiará de fase y amplitud (aunque no de frecuencia). Para mantener la emisión se debe excitar el átomo cada cierto tiempo, menor que el tiempo de desexcitación. Es fundamentalmente el cambio de fase cada vez que se estimula el átomo mediante un choque (por ejemplo, cada \(10^{-10} s\) ) el que impide que la onda emitida sea monocromática. Este salto de fase depende de muchos parámetros de la excitación y, en general, es incontrolable. Para muchas aplicaciones esta no monocromaticidad no es de monocromaticidad no es suficiente.

La cantidad de frecuencias que contiene una onda depende del tiempo entre saltos de fase (una especie de principio de incertidumbre energía-tiempo)

\[
\Delta \omega \propto \frac{1}{\delta t} \notag
\]

\(\mathrm{Al}\) tiempo \(\delta t\) se le llama tiempo de coherencia. Como \(\delta t\) es aleatorio, se define de modo estadístico. Como cuantificador de la monocromaticidad usamos la cantidad \(\frac{\Delta \omega}{\omega}\). En el caso que nos ocupa

\[
\frac{\Delta \omega}{\omega} \propto \frac{1}{\omega \delta t} \simeq 10^{-5} \notag
\]

lo que indica una alta monocromaticidad. Cotas de mayor monocromaticidad se alcanzan con el uso de la radiación estimulada (laser). Igual que hay ondas más monocromáticas, las hay mucho menos: por ejemplo, los átomos en un gas experimentan colisiones entre ellos, y el tiempo de coherencia disminuye con la presión y la temperatura, que favorecen las colisiones.

Cuando tenemos dos átomos radiando según este esquema la diferencia de fases entre ambos, \(g_{2}-g_{1}\) es una variable aleatoria que cambia a saltos en tiempos siempre menores a \(\delta t \simeq 10^{-10} s .\) El promedio temporal del término de interferencia es nulo y por lo tanto, a pesar de ser la onda bastante monocromática, no hay interferencia. Concluimos que las ondas de dos fuentes independientes son incoherentes.


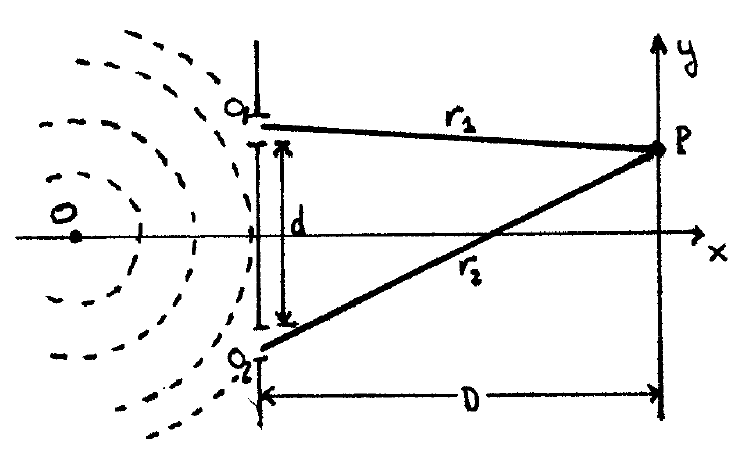
Figura 9.3: División de la onda procendente de una fuente. Una de las partes llega al punto de reunión en un tiempo \(\Delta t\) y otra en \(\Delta t+\tau\).

No veremos interferencia a menos que los cambios de fase se produzcan en el mismo instante para las dos ondas, es decir, a menos que sean las mismas. Si superponemos una onda consigo misma sí hay coherencia.

\[
E(t-\Delta t)+E(t-\Delta t-\tau)=E_{1}+E_{2} \notag
\]

La diferencia de fases ya no será aleatoria y el promedio temporal del término de interferencia podrá ser distinto de cero. Con una salvedad: las dos ondas producidas por una misma fuente una onda pueden llevar un retraso relativo pero no demasiado grande. Si retrasamos una onda respecto a la otra un tiempo superior a \(\delta t\) volveremos a tener dos ondas con diferencia de fase aleatoria. Habrá interferencia si \(\tau \ll \delta t\) (ondas coherentes) y no la habrá si \(\tau>\delta t\) (ondas incoherentes).

Resumiendo

• Para observar la interferencia en las mejores condiciones hemos supuesto que ambas ondas tienen el mismo estado de polarización, lo que nos permite hacer una descripción escalar que es más sencilla.

\[
\mathbf{E}_{i}=E_{i} \mathbf{u} \notag
\]

• Hemos preferido estudiar interferencias independientes del tiempo. Por lo tanto la frecuencia de las ondas que interfieren debe ser estrictamente igual.

\[
\omega_{1}=\omega_{2} \notag
\]

• Estos requisitos, junto con el hecho de que las ondas de emisores distintos son incoherentes nos han llevado a requerir que las ondas sean producidas por la misma fuente.
• Esto no sirve de nada si ambas ondas tienen una diferencia de camino tan grande que el retardo relativo supera el tiempo de coherencia.

\[
\tau \ll \delta t \notag
\]

A partir de aquí sólo queda catalogar los interferómetros. Estudiaremos aquí sólo los ejemplos más famosos.

Figura \(\PageIndex{2}\): La idea consiste en atrapar dos trozos del frente de ondas y luego reunirlos.

Figura \(\PageIndex{3}\): Coordenadas de los puntos de emisión y el punto de observación.