9.4.3: Sustitución de todo el interferómetro por dos imágenes
- Page ID
- 51189
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Si miramos desde la pantalla de observación, veremos dos imágenes de la fuente. Todo el montaje se hace equivalente a dos fuentes idénticas-coherentes-separadas (que es lo que necesitamos para observar interferencia). Estas imágenes están sobre la misma línea, una a una distancia aparente del centro del divisor de haz \(2 d_{1}+l\) y otra a distancia \(2 d_{2}+l\). La distancia que separa a estas fuentes coherentes es \(2\left(d_{1}-d_{2}\right)=2 d\).
Al ser fuentes puntuales podemos suponer que emiten ondas esféricas, y sólo queda resolver el problema del interferómetro de YOUNG con una geometría ligeramente diferente.
\[
I=I_{1}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \left(k\left(r_{2}-r_{1}\right)+\delta\right) \notag
\]
Hemos añadido una fase extra \(\delta\) para dar cuenta de las reflexiones que se produzcan en el divisor de haz, que es un medio absorbente. Si el divisor de haz es al \(50 \%\) se cumple \(I_{1} \simeq I_{2}\).
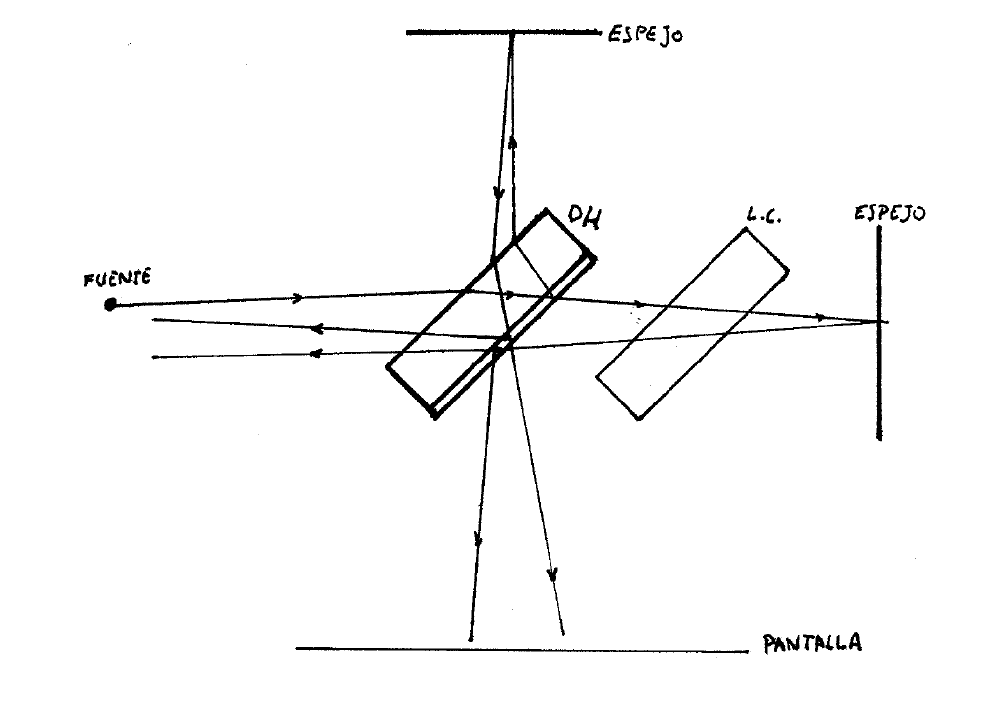
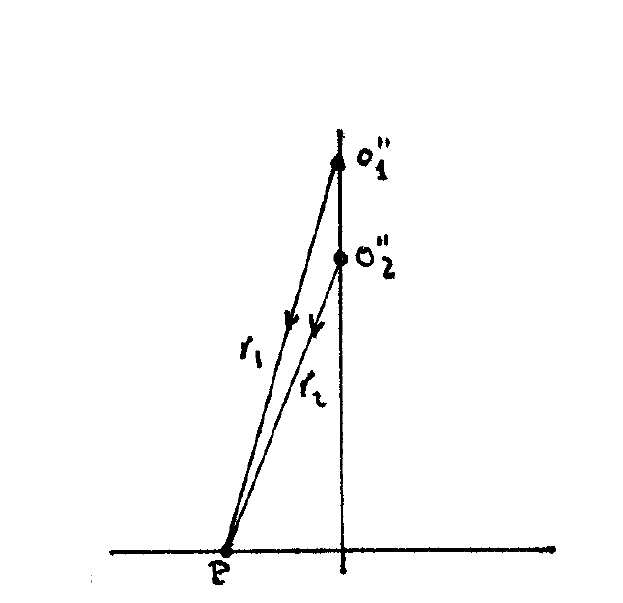
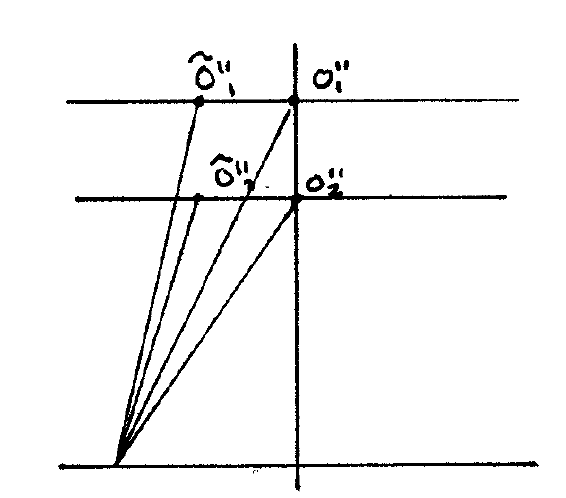
Figura de interferencia
Como el sistema tiene simetría de revolución alrededor de la recta que une las dos imágenes, según el principio de CuRIE ("los efectos tienen las simetrías de las causas"), pensamos que la figura de interferencia será una serie de anillos concéntricos, alternativamente claros y oscuros. Nosotros no vamos a precisar más su aspecto, aunque no es especialmente difícil hacerlo.
Fuentes extensas
Nos interesa saber cómo es la figura cuando la fuente está constituída por una infinidad de puntos incoherentes entre sí. El interés de este caso radica en la intensidad extra que las fuentes extensas proporcionan y que hace el fenómeno verdaderamente observable.
El interferómetro opera como hemos descrito, creando dos imágenes de la fuente original coherentes entre sí. Todos los puntos de la fuente dan lugar a dos imágenes. Cada pareja de estas dará lugar a su sistema de anillos, sin que haya interferencias cruzadas (de la imagen de un punto con la de otro). El problema es que los infinitos sistemas de anillos no coinciden entre sí: el camino óptico \(r_{2}-r_{1}\) para una pareja y \(\hat{r}_{2}-\hat{r}_{1}\) para otra son distintos. Eso destruye la interferencia, puesto que habrá una mezcla espacial más extensa sea la fuente.
Hay un caso, empero, en el que no se produce pérdida de visibilidad. En efecto, si llevamos la pantalla a una distancia infinita (en la práctica, colocando la pantalla en el plano focal imagen de una lente convergente \({ }^{1}\) ), las diferencias de fase son las mismas para todas las parejas de puntos imagen. Veamos por qué. Si consideramos el plano \(\Sigma\), perpendicular al haz paralelo proveniente de las imágenes extensas, podemos convencernos de que \(\Sigma \rightarrow P\) es el mismo camino óptico para todas las ondas. Teniendo en cuenta las cantidades \(\Delta\) y \(\theta\) la diferencia de camino óptico es \(n \Delta\) para ambas parejas de

imágenes-fuente. \(\Delta=2 d \cos \theta\), por lo que la diferencia de fase vale
\[
\frac{2 \pi}{\lambda} n \Delta=\frac{2 \pi}{\lambda} 2 n d \cos \theta \notag
\]
si el divisor de haz es al \(50 \%\) las intensidades tendrán la distribución
\[
I(\theta)=2 I_{0}\left(1+\cos \left(\frac{2 \pi}{\lambda} 2 n d \cos \theta+\delta\right)\right) \notag
\]
Los puntos de observación en la pantalla están parametrizados por el ángulo \(\theta\) (tenemos anillos centrados en el foco de la lente). La condición de máximo es
\[
\left(\frac{2 \pi}{\lambda} 2 n d \cos \theta+\delta\right)=2 \pi M \notag
\]
donde \(M \in \mathcal{Z}\) es el orden del máximo. La utilidad de estos fenómenos es la determinación de longitudes (de onda, o distancias entre las imágenes, que son, en definitiva, distancias entre los espejos). Son así de precisos en razón de la fuerte dependencia de la figura interferencial en función de dichas longitudes. Lo mismo se puede decir respecto al índice de refracción.
_______________________________________________________________
1. Cuando se hace el montaje experimental, mirar directamente a las imágenes-fuente extensas equivale a }}\) introducir una lente convergente, pues el ojo relajado ( \(\sin\) acomodación) hace perfectamente esta función.

