5.9: Más sobre la Ecuación de Transferencia

Consulte la ecuación 5.5.1. Vemos por lo que posteriormente se había discutido eso\([\alpha(\nu) + \sigma(\nu)]dx = d\tau(\nu)\) y aquello\(j_\nu dx = d\tau(\nu)\). Por lo tanto

\[\frac{dI_v}{d\tau(\nu)} = S_\nu - I_\nu , \label{5.9.1}\]

y esta es otra forma de la ecuación de transferencia.

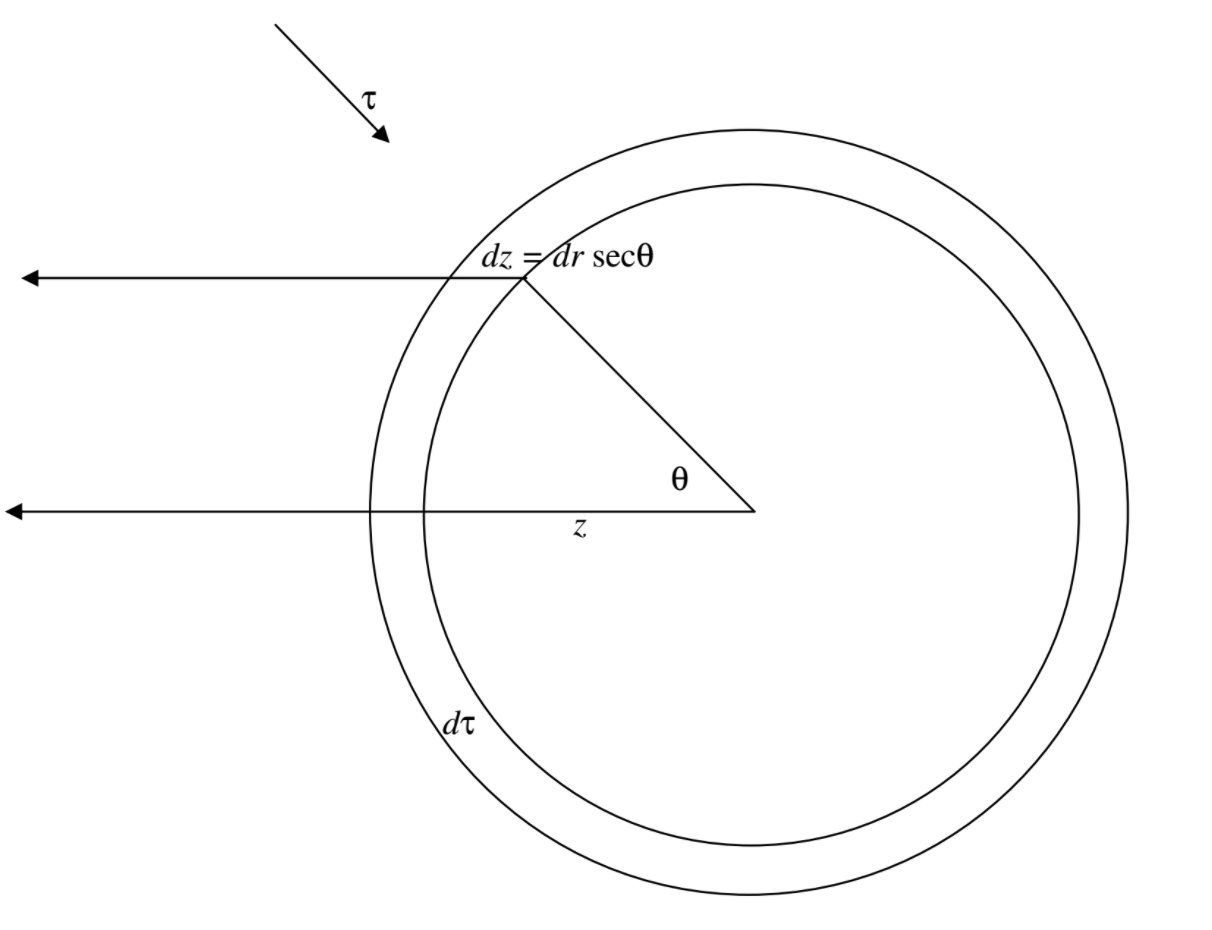
Consideremos ahora una estrella esférica con una atmósfera poco profunda (“atmósfera paralela plana”). En la figura\(\text{V.6}\), la distancia radial\(r\) se mide radialmente hacia afuera desde el centro de la estrella. La profundidad óptica se mide desde el exterior hacia el centro de la estrella. El grosor de la capa es\(dr\). La coordenada\(z\) se mide desde el centro de la estrella hacia el observador, y la longitud del camino a través de la atmósfera en esa dirección en ángulo\(\theta\) es\(dz = dr \sec \theta\). La ecuación de transferencia se puede escribir

\[dI_\nu (\theta) = - [\kappa (\nu) I_\nu (\theta) - j_\nu] dz. \label{5.9.2}\]

Ahora\(\kappa (\nu) dz = -\sec \theta d\tau(\nu)\) y\(j_\nu = \kappa (\nu) S_\nu\). Por lo tanto

\[\cos \theta \frac{dI_{\nu}(\theta)}{d\tau (\nu)} = I_{\nu} (\theta) - S_\nu \label{5.9.3}\]

Esta es otra forma más de la ecuación de transferencia. La cantidad a menudo\(\cos\theta\) se escribe\(\mu\), por lo que esa ecuación a menudo\(\ref{5.9.3}\) se escribe

\[\mu\frac{dI_v(\theta)}{d\tau(\nu)} = I_\nu(\theta) - S_\nu \label{5.9.4}\]

\(\text{FIGURE V.6}\)

Hagamos\(\frac{1}{4\pi} \oint d\omega\) a cada término en ecuación\(\ref{5.9.4}\). Por\(\oint\) me refiero a integrar sobre los\(4\pi\) esteradianos. En coordenadas esféricas\(d \omega = \sin \theta d \theta d \phi\). Obtenemos

\[\frac{1}{4\pi} \oint \frac{dI_\nu (\theta)}{d \tau(\nu)} \cos \theta d \omega = \frac{1}{4 \pi} \oint I_\nu d \omega - \frac{1}{4 \pi} \oint S_\nu d \omega \label{5.9.5}\]

El lado izquierdo es\(dH_\nu/d\tau(\nu)\) y el primer término en el lado derecho es\(J_\nu\). (Ver las definiciones - ecuaciones 4.5.2 y 4.7.1.) En el caso de la dispersión isotrópica, la función fuente es isotrópica de manera que, en este caso

\[\frac{dH_\nu}{d\tau(\nu)} = J_\nu - S_\nu, \label{5.9.6}\]

y esta es otra forma de la ecuación de transferencia.

Por otro lado, si hacemos\(\frac{1}{4\pi} \oint \cos \theta d \omega\) a cada término en la ecuación 5.15, obtenemos

\[\frac{1}{4\pi} \oint \frac{dI_\nu(\theta)}{d\tau(\nu)} \cos^2 \theta d \omega = \frac{1}{4\pi} \oint I_\nu \cos \theta d \omega - \frac{1}{4\pi} \oint S_\nu \cos \theta d \omega \label{5.9.7}\]

En el caso de la dispersión isotrópica la última integral es cero, de manera que

\[\frac{dK_\nu}{d\tau(\nu)} = H_\nu , \label{5.9.8}\]

y esta es otra forma más de la ecuación de transferencia.

Ahora\(H_\nu\) es independiente de la profundidad óptica (¿por qué? - en una atmósfera plana paralela, esto solo expresa el hecho de que el flujo (vatios por metro cuadrado) se conserva), por lo que podemos integrar la ecuación\(\ref{5.9.8}\) para obtener

\[K_\nu = H_\nu \tau(\nu) + \text{constant} \label{5.9.9}\]

Obsérvese también que\(H_\nu = F_\nu /(4\pi)\), y, si la radiación es isotrópica, de\(K_\nu = J_\nu/ 3\) manera que,

\[J_\nu = \frac{3 F_\nu \tau(\nu)}{4\pi} + J_\nu(0) \label{5.9.10}\]

donde\(J_\nu(0)\) es la intensidad específica media (resplandor) en la superficie, que es la mitad de la intensidad específica en la superficie (ya que el resplandor del cielo sobre la superficie es cero). Así

\[J_\nu (0) = \frac{1}{2} I_\nu (0) = F_\nu / (2\pi) \label{5.9.11}\]

Por lo tanto

\[J_\nu = \frac{F_\nu}{2\pi} \left( 1 + \frac{3}{2} \tau ( \nu ) \right) \label{5.9.12}\]

Esto muestra, a este grado de aproximación (que incluye la aproximación de que la radiación en la atmósfera es isotrópica -que puede ser el caso exactamente solo en el centro de la estrella) cómo la intensidad específica media aumenta con la profundidad óptica.

Dejar\(T\) ser la temperatura a profundidad óptica\(\tau\).

Dejar\(T_0\) ser la temperatura de la superficie.

Dejar\(T_{\text{eff}}\) ser la temperatura efectiva, definida por\(F(0) = \sigma T^4_{\text{eff}}\),

También tenemos\(\pi J = \sigma T^4\) y\( \pi J (0) = \sigma T_0^4 = \frac{1}{2} F\).

De estos encontramos las siguientes relaciones entre estas temperaturas:

\[T^4 = \left( 1 + \frac{3}{2} \tau \right) T^4_0 = \frac{1}{2} \left( 1 + \frac{3}{2} \tau \right) T^4_{\text{eff}} \label{5.9.13}\]

\[T_0^4 = \frac{2}{2+3\pi}T^4 = \frac{1}{2} T^4_{\text{eff}} \label{5.9.14}\]

\[T^4_{\text{eff}} = \frac{4}{2+3\tau}T^4 = 2 T^4_0 \label{5.9.15}\]

Tenga en cuenta también que\(T = T_{\text{eff}}\) en\(\tau = 2/3\), y\(T = T_0\) en\(\tau = 0\).