10.1: Amplamiento Natural (Amortiguación de Radiación)

El modelo de oscilador clásico del átomo fue descrito en la Sección 9.2. En este modelo, el movimiento del electrón óptico, cuando está sujeto al campo electromagnético variable de una onda de luz, obedece a la ecuación diferencial para el movimiento forzado, amortiguado y oscilatorio:

\[\label{10.2.1}\ddot x+\gamma \dot x +\omega_0^2x=\frac{e\hat{E}}{m}\cos \omega t.\]

Debido a que el electrón oscilante (por lo tanto acelerante) mismo irradia, el sistema pierde energía, lo que equivale a decir que el movimiento está amortiguado, y\(\gamma\) es la constante de amortiguación. La teoría electromagnética nos dice que la tasa de radiación de la energía de un electrón acelerante es

\[\label{10.2.2}\frac{2}{3}\cdot \frac{e^2\ddot x^2}{4\pi ε_0c^3}.\]

(El lector, como siempre, debe verificar las dimensiones de esta y todas las expresiones posteriores).

Para un electrón que está oscilando, la tasa promedio de pérdida de energía por ciclo es

\[\label{10.2.3}\frac{2}{3}\cdot \frac{e^2 \overline{\ddot x^2}}{4\pi ε_0 c^3}.\]

Aquí la barra denota el valor promedio a lo largo de un ciclo.

Si la amplitud y frecuencia angular de la oscilación son\(a\) y\(\omega_0\), la aceleración máxima es\(a\omega_0^2\) y la aceleración cuadrada media es\(\frac{1}{2}a^2\omega_0^4\). La energía (cinética más potencial) del electrón oscilante es

\[\label{10.2.4}W=\frac{1}{2}ma^2\omega_0^2.\]

Así podemos escribir para la tasa promedio de pérdida por ciclo de energía del sistema por radiación electromagnética:

\[\label{10.2.5}\frac{2}{3}\cdot\frac{e^2\omega_0^2}{4\pi ε_0 mc^3}\cdot W\]

Por lo tanto, la energía se cae según

\[\label{10.2.6}\dot W = -\frac{1}{3}\cdot \frac{e^2 \omega_0^2}{4\pi ε_0 mc^3}\cdot W.\]

La longitud de onda irradiada viene dada por\(\lambda = 2\pi c /\omega_0\), de modo que la Ecuación\ ref {10.2.6} se convierte

\[\dot W = -\frac{2\pi e^2}{3ε_0 mc \lambda^2}\cdot W.\label{10.2.7}\]

Se recordará de la teoría de las oscilaciones ligeramente amortiguadas que la solución a la Ecuación\ ref {10.2.1} muestra que la amplitud se cae con el tiempo as\(\text{exp}(-\frac{1}{2} \gamma t)\), y que la energía cae como\(\text{exp}(-\gamma t)\). Así identificamos el coeficiente de\(W\) en el lado derecho de la Ecuación\ ref {10.2.7} como la constante clásica de amortiguación de radiación\(\gamma\):

\[\label{10.2.8}\gamma =\frac{2\pi e^2}{3ε_0mc\lambda^2}.\]

Numéricamente, si\(\gamma\) está en\(\text{s}^{-1}\) y\(\lambda\) está en\(\text{m}\),

\[\label{10.2.9}\gamma = \frac{2.223 \times 10^{-5}}{\lambda^2}.\]

Ahora vamos a calcular la velocidad a la que la energía es transportada por unidad de área por una onda electromagnética, y también a calcular la velocidad a la que una losa ópticamente delgada de un gas de osciladores clásicos absorbe energía, y de ahí vamos a calcular el coeficiente de absorción clásico. Comenzamos recordando, desde el electromagnetismo elemental, que la energía retenida por unidad de volumen en un campo eléctrico es\(\frac{1}{2}\textbf{D}\cdot \textbf{E}\) y la energía retenida por unidad de volumen en un campo magnético lo es\(\frac{1}{2}\textbf{B}\cdot \textbf{H}\). En un medio isotrópico, estos se convierten\(\frac{1}{2}ε E^2\) y\(\frac{1}{2}\mu H^2\), y, al vacío, se vuelven\(\frac{1}{2}ε_0E^2 \text{ and }\frac{1}{2}\mu_0H^2\).

Para un campo eléctrico oscilante de la forma\(E = \hat{E} \cos \omega t\), la energía promedio por unidad de volumen por ciclo es\(\frac{1}{2}ε_0 \overline{E^2} = \frac{1}{4}ε_0 \hat{E}^2\). De manera similar para un campo magnético oscilante, la energía promedio por unidad de volumen por ciclo es\(\frac{1}{4}\mu_0 \hat{H}^2\). Una onda electromagnética consiste en una onda eléctrica y una magnética que se mueven a velocidad\(c\), por lo que la velocidad a la que se transmite la energía a través de la unidad de área es\(\left ( \frac{1}{4}ε_0 \hat{E}^2+\frac{1}{4}\mu_0\hat{H}^2\right ) c\), y las dos partes son iguales, de manera que la velocidad a la que se transmite energía por unidad de área por una onda electromagnética plana es\(\frac{1}{2}ε_0 \hat{E}^2c\).

Ahora estamos modelando el oscilador clásico como un electrón unido a un átomo, y estando sujeto a una fuerza periódica\(\frac{e\hat{E}}{m}\cos \omega t\) de una onda electromagnética. La tasa de absorción de energía por dicho oscilador (véase, por ejemplo, el Capítulo 12 de Mecánica Clásica es

\[\frac{\gamma e^2 \hat{E}^2\omega^2}{2m[(\omega_0^2-\omega^2)^2+\gamma^2\omega^2]}.\nonumber\]

Imaginamos una onda electromagnética plana que llega a (irradiar) una losa de gas que contiene osciladores\(\mathcal{N}\) clásicos por unidad de área, o\(n\) por unidad de volumen. El índice de llegada de energía por unidad de superficie, hemos visto, es\(\frac{1}{2}ε_0 \hat{E}^2c\). La tasa de absorción de energía por unidad de área es

\[\frac{\mathcal{N}\gamma e^2\hat{E}^2\omega^2}{2m[(\omega_0^2-\omega^2)^2+\gamma^2\omega^2]}.\nonumber\]

Por lo tanto, la absorbancia (ver capítulo 2, sección 2.2) es

\[\label{10.2.10}a=\frac{\mathcal{N}\gamma e^2 \omega^2}{mε_0 c[(\omega_0^2-\omega^2)^2+\gamma^2\omega^2]}.\]

y el coeficiente de absorción lineal es

\[\label{10.2.11}\alpha = \frac{n\gamma e^2 \omega^2}{mε_0 c[(\omega_0^2-\omega^2)^2+\gamma^2\omega^2]}.\]

Un recordatorio aquí podría estar en orden. La absorbancia\(a\) se define en la sección 2.2, y en la notación de la figura IX.1, la absorbancia a la longitud de onda\(\lambda\) sería\(\left ( I_\lambda (c)-I_\lambda(\lambda)\right )/I_\lambda (c)\). \(\alpha\)El coeficiente de absorción se define por la ecuación 5.2.1:\(- dI/I = \alpha\,dx\). Para una rebanada gruesa de gas, de espesor\(t\), ésta se integra, en la notación de la figura IX.1, a\(I_\lambda (\lambda)= I_\lambda (c) \text{exp}(-\alpha t)\). Pero para un gas ópticamente delgado, que es lo que estamos considerando, a menos que se indique lo contrario, en este capítulo, esto se vuelve\(\left ( I_\lambda (c) - I_\lambda (\lambda)\right )/ I_\lambda (c) = \alpha t\). Así, para un gas ópticamente delgado, la absorbancia es solo coeficiente de absorción por espesor del gas. Y la relación entre densidad de partículas\(n\) y densidad de columna\(\mathcal{N}\text{ is }\mathcal{N} = nt\).

Podemos escribir\(\omega_0^2 -\omega = \left ( \omega_0 -\omega \right ) \left ( \omega_0 + \omega \right )\). Escribamos también\(\omega\) como\(2\pi ν\). También, en las inmediaciones de la línea, hagamos la aproximación\(\omega_0 + \omega = 2\omega\). Luego obtenemos para el coeficiente de absorción, en las inmediaciones de la línea,

\[\label{10.2.12}\alpha = \frac{\gamma n e^2}{16\pi^2 mcε_0 \left [ (\nu-\nu_0)^2+\left ( \frac{\gamma }{4\pi}\right )^2\right ]} .\]

Ejercicio\(\PageIndex{1}\)

Asegúrate de que no he cometido errores al derivar ecuaciones\ ref {10.2.10} ,11 y 12, y comprueba las dimensiones de cada expresión a medida que avanzas. Avísame si encuentras algo mal.

Ahora el ancho equivalente en unidades de frecuencia de una línea de absorción en una capa ópticamente delgada de gas de espesor geométrico\(t\) es (ver ecuación 9.1.6)

\[\label{10.2.13}W^{(\nu)}=t\int_{-\infty}^\infty \alpha d(\nu-\nu_0).\]

Ejercicio\(\PageIndex{2}\)

(a) Para aquellos lectores que (comprensiblemente) objetan esa expresión\ ref {10.2.12} es válida sólo en las inmediaciones de la línea, y por lo tanto que no podemos integrarnos desde\(-\infty \text{ to }+\infty\), integrar expresión\ ref {10.2.11} de\(0\text{ to }\infty\).

(b) Para el resto de nosotros, integrar la Ecuación\ ref {10.2.11} de\(ν - ν_0 = -\infty\text{ to }+ \infty\). Una sustitución probablemente\(4\pi (ν - ν_0 ) = \gamma \tan \theta\) será un buen comienzo.

Obtenemos

\[\label{10.2.14}W^{(\nu)}=\frac{\mathcal{N}e^2}{4mcε_0}=2.654\times 10^{-6}\mathcal{N},\]

dónde\(W^{(\nu)}\) está adentro\(\text{Hz}\) y\(\mathcal{N}\) está adentro\(\text{m}^{-2}\). Así, el modelo de oscilador clásico predice que el ancho equivalente en unidades de frecuencia es independiente de la frecuencia (y por lo tanto de la longitud de onda) de la línea, y también independiente de la constante de amortiguación. Si expresamos el ancho equivalente en unidades de longitud de onda (ver ecuación 9.1.3), obtenemos:

\[\label{10.2.15}W=\frac{\mathcal{N}e^2\lambda^2}{4mc^2ε_0}.\]

Esto es lo mismo que la ecuación 9.2.2.

Cuando discutimos esta ecuación en el Capítulo 9, señalamos que los anchos equivalentes de las líneas reales difieren de esta predicción por un factor\(f_{12}\), la fuerza del oscilador de absorción, y también señalamos que\(\mathcal{N}\) tiene que ser reemplazado por\(\mathcal{N}_1\), la densidad de la columna de átomos en la inicial ( inferior). Así, a partir de este punto, voy a\(\mathcal{N}\) sustituir por\(\mathcal{N}_1f_{12}\). No obstante, en este capítulo no nos preocupa tanto el ancho equivalente, sino el perfil de línea y el ancho real. El ancho de una línea de emisión en este contexto se expresa comúnmente como el ancho completo a la mitad del máximo (FWHM) y el ancho de una línea de absorción como el ancho completo a la mitad mínima (FWHm). (Estos no deben confundirse con el ancho equivalente, lo cual se discute en la sección 9.1.) Tenga en cuenta que algunos escritores utilizan el término “medio ancho”. Generalmente no es posible saber qué quiere decir un escritor con esto.

En términos de la notación de la figura IX.1 (en la que “\(\text{c}\)” denota “continuo”), pero usando una frecuencia en lugar de una escala de longitud de onda, la absorbancia a la frecuencia\(ν\) es

\[\label{10.2.16}a(\nu)=\frac{I_\nu(\text{c})-I_\nu(\nu)}{I_\nu(\text{c})}.\]

Así, el perfil de una línea de absorción viene dado por

\[\label{10.2.17}I_\nu(\nu)=I_\nu(\text{c})\left (1-a(\nu)\right ).\]

Para amortiguar la radiación tenemos

\[\label{10.2.18}a(\nu)=\frac{\gamma \mathcal{N}_1 f_{12}e^2}{16\pi^2mcε_0\left [ (\nu-\nu_0)^2+\left ( \frac{\gamma}{4\pi}\right )^2\right ] }.\]

El valor máximo de la absorbancia (en el centro de la línea) es

\[\label{10.2.19}a(\nu_0)=\frac{\mathcal{N}_1f_{12}e^2}{mcε_0 \gamma}.\]

Esta cantidad es también\(\frac{I_\nu(\text{c})-I_\nu(\nu_0)}{I_\nu(\text{c})}\) y también se conoce como la profundidad central\(d\) de la línea. (Asegúrese de referirse a la figura IX.1 para entender su significado.) Utilizaré el símbolo\(d\text{ or }a(\nu_0)\) indistintamente, según el contexto.

Es fácil ver que el valor\(\nu-\nu_0\) al que la absorbancia es la mitad de su valor máximo es\(\gamma /(4\pi)\). Es decir, el ancho completo a la mitad máxima (FWHM) de la absorbancia, que denoto como\(w\), es, en unidades de frecuencia:

\[\label{10.2.20}w=\frac{\gamma}{2\pi}.\]

(En unidades de longitud de onda, es\(\lambda^2 /c\) veces esto.) Esta es también la fWHM del perfil de absorción.

La ecuación\ ref {10.2.18} se puede escribir

\[\label{10.2.21}\frac{a(\nu)}{a(\nu_0)}=\frac{1}{4\left ( \frac{\nu-\nu_0}{w}\right )^2+1}.\]

Se puede escribir el perfil de la línea de absorción (ver Ecuación\ ref {10.2.1})

\[\label{10.2.22}\frac{I_\nu(\nu)}{I_\nu(\text{c})}=1-\frac{d}{4\left ( \frac{\nu-\nu_0}{w}\right )^2+1}.\]

Observe que en el centro de la línea,\(I_\nu(\nu_0)/I_\nu(\text{c}) = 1\) menos la profundidad central; y muy lejos del centro de la línea\(I_\nu(\nu) = I_\nu(\text{c})\), como se esperaba. Este tipo de perfil se denomina perfil de Lorentz.

De las ecuaciones\ ref {10.2.14} (pero con\(\mathcal{N}_1f_{12}\) sustituido por\(\mathcal{N}\)),\ ref {10.2.19} y\ ref {10.2.20}, encontramos que

\[\nonumber \begin{align}\text{Equivalent width}&=\frac{\pi}{2}\times\text{ central depth }\times\text{ FWHm} \\ &1.571\times \text{ central depth }\times \text{ FWHm}. \\ \end{align}\]

Esto es cierto si el ancho equivalente y fWHm se miden en frecuencia o en unidades de longitud de onda. (Es una lástima que, para el trabajo teórico, la frecuencia sea más conveniente que la longitud de onda, ya que la frecuencia es proporcional a la energía, pero los experimentalistas a menudo (¡no invariablemente!) trabajar con rejillas, que dispersan la luz linealmente con respecto a la longitud de onda!)

De hecho, el ancho equivalente de cualquier tipo de perfil se puede escribir en la forma

\[\label{10.2.24}\text{Equivalent width }=\text{ constant }\times\text{ central depth }\times\text{ FWHm },\]

el valor de la constante dependiendo del tipo de perfil.

En días fotográficos, la medición de anchuras equivalentes fue un procedimiento muy laborioso, y, si uno tuviera buenas razones para creer que los perfiles de línea en un espectro eran todos lorentzianos, el equivalente con se encontraría midiendo solo la fWHM y la profundidad central. Incluso hoy en día, cuando los anchos equivalentes a menudo pueden ser determinados por computadora a partir de espectros grabados digitalmente casi instantáneamente, puede haber ocasiones en las que los espectros de baja resolución no lo permitan, y todo lo que se puede medir honestamente son las profundidades centrales y anchuras equivalentes. El tipo de perfil, y de ahí el valor a utilizar para la constante en la Ecuación\ ref {10.2.14}, requiere un salto de fe.

Cabe señalar (consultar ecuaciones\ ref {10.2.4},\ ref {10.2.19} y\ ref {10.2.20}) que el ancho equivalente está determinado por la densidad de columna de los átomos absorbentes (o, más bien, on\(\mathcal{N}_1f_{12}\)), el fWHm está determinado por la constante de amortiguación, pero la profundidad central depende de ambos. Se puede determinar la constante de amortiguación midiendo el FWHm.

La forma del perfil de Lorentz se muestra en la figura X.1 para dos líneas, una con una profundidad central de 0.8 y la otra con una profundidad central de 0.4. Ambas líneas tienen el mismo ancho equivalente,\(wd\) siendo el producto el mismo para cada una. Tenga en cuenta que este tipo de perfil tiene un núcleo estrecho, bordeado por extensas alas.

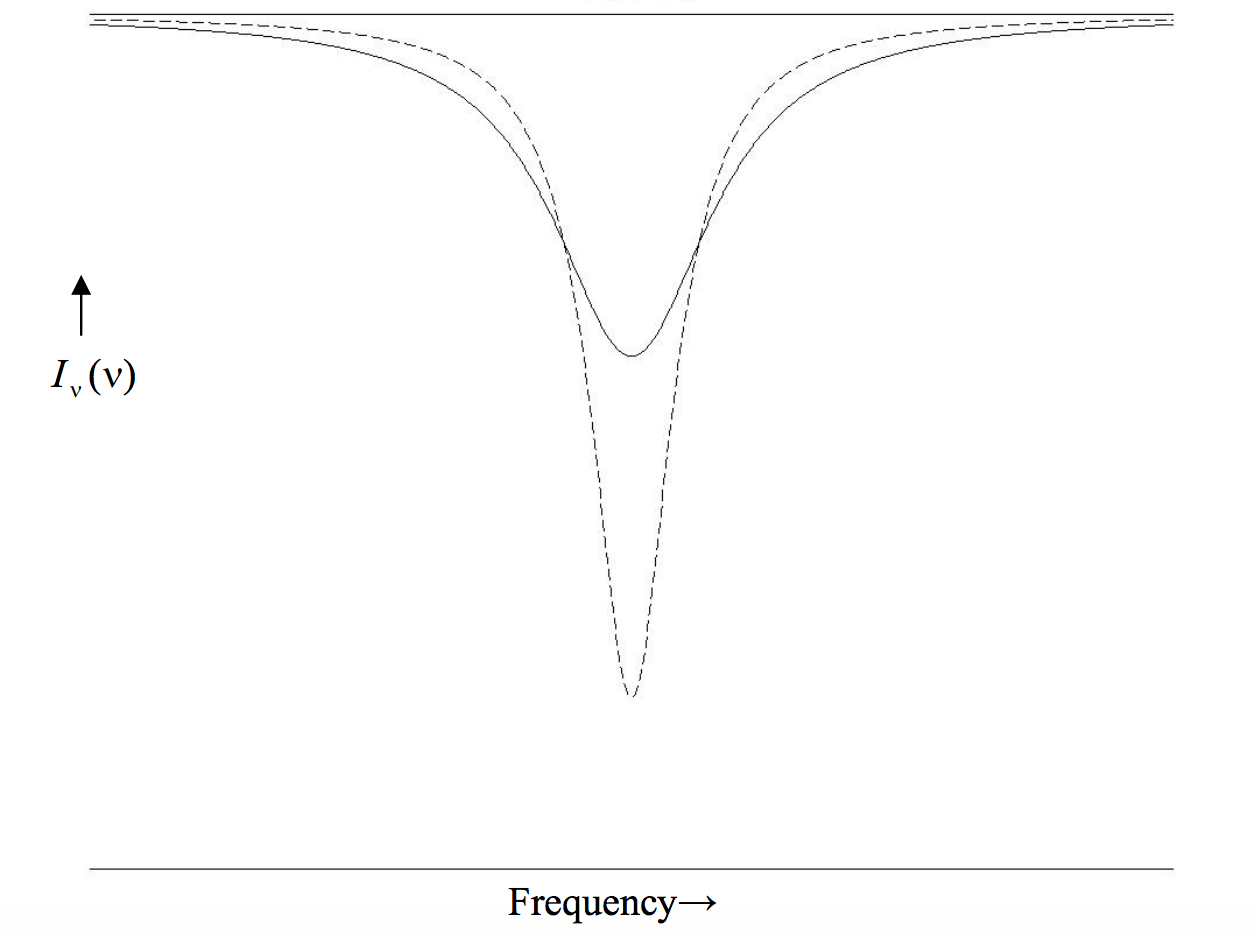
\(\text{FIGURE X.1}\)

Por supuesto, una inspección visual de un perfil que muestra un núcleo estrecho y alas extensas, aunque sugerente, no prueba que el perfil sea estrictamente lorentziano. Sin embargo, la ecuación\ ref {10.2.22} se puede reorganizar para que se lea

\[\label{10.2.25}\frac{I_\nu(\text{c})}{I_\nu(\text{c})-I_\nu(\nu)}=\frac{4}{w^2d}\left (\nu-\nu_0 \right )^2+\frac{1}{d^2}.\]

Esto muestra que si haces una serie de medidas\(I_ν(ν)\) y trazas una gráfica del lado izquierdo versus\((ν-ν_0)^2\), debes obtener una línea recta si el perfil es lorentziano, y obtendrás la profundidad central y el ancho equivalente (de ahí también la constante de amortiguación y la densidad de la columna) de el intercepto y la pendiente como bono. Y si no consigues una línea recta, no tienes un perfil de Lorentz.

Se recordará que la teoría puramente clásica del oscilador predijo que las anchuras equivalentes de todas las líneas (en unidades de frecuencia) de un elemento dado son las mismas, es decir, la dada por la Ecuación\ ref {10.2.14}. La obvia observación de que esto no es así nos llevó a introducir la fuerza del oscilador de emisión, y también a sustituir\(\mathcal{N}\text{ by }\mathcal{N}_1\). Asimismo, la ecuación\ ref {10.2.20} predice que el fWHm (en unidades de longitud de onda) es el mismo para todas las líneas. (La Ecuación 10.2.20 da el FWHm en unidades de frecuencia. Para entender mi advertencia “en unidades de longitud de onda”, refiérase también a las ecuaciones\ ref {10.2.8} y\ ref {10.2.9}. Verá que el fWHm predicho en unidades de longitud de onda es\(\frac{e^2}{3\epsilon_0mc^2}=1.18\times 10^{-14}\text{m}\), que es extremadamente pequeño, y el núcleo, al menos, está más allá de la resolución de la mayoría de los espectrógrafos.) Obviamente las constantes de amortiguación para líneas reales son mucho mayores que esto. Para líneas reales, la constante de amortiguación clásica\(\gamma\) tiene que ser reemplazada por la constante de amortiguación mecánica cuántica\(\Gamma\).

Actualmente estoy describiendo de una manera muy cualitativa el tratamiento mecánico cuántico de la constante de amortiguación. Quantum mecánicamente, una onda electromagnética es tratada como una perturbación para el operador hamiltoniano. Hemos visto en la sección 9.4 que cada nivel tiene una vida útil finita — ver especialmente la ecuación 9.4.7. La vida media para un nivel\(m\text{ is }1/\Gamma_m\). Cada nivel no es infinitesimalmente estrecho. Es decir, no se puede decir con precisión infinitesimal cuál es la energía de un nivel (o estado) dado. La incertidumbre de la energía y la vida media se relacionan a través del principio de incertidumbre de Heisenberg. Cuanto más larga sea la vida, más amplio será el nivel. La probabilidad energética de un nivel\(m\) viene dada por una función Lorentz con parámetro\(\Gamma_m\), dada por la ecuación 9.4.7 e igual al recíproco de la vida media. De igual manera un nivel\(n\) tiene una distribución de probabilidad de energía dada por una función de Lorentz con parámetro\(\Gamma_n\). Cuando un átomo hace una transición entre\(m\text{ and }n\), naturalmente, hay una incertidumbre energética en el fotón emitido o absorbido, y así hay una distribución de fotones (es decir, un perfil de línea) que es una función de Lorentz con parámetro\(\Gamma = \Gamma_m + \Gamma_n\). Este parámetro\(\Gamma\) debe reemplazar la constante de amortiguación clásica\(\gamma\). El fWHm de una línea, en unidades de frecuencia, es ahora\(\Gamma/(2\pi)\), que varía de línea a línea.

Desafortunadamente se observa, al menos en el espectro de las estrellas de secuencia principal, si no en el de gigantes y supergigantes, ¡que los FWHM de la mayoría de las líneas son casi iguales! ¡Qué frustrante! La teoría clásica predice que todas las líneas tienen el mismo FWHM. Sabemos que la teoría clásica está equivocada, así que nos tomamos la molestia de hacer teoría mecánica cuántica, que predice diferentes FWHM de línea a línea. Y luego vamos a observar las estrellas de la secuencia principal y nos encontramos con que todas las líneas tienen el mismo fWhM (ciertamente mucho más amplio de lo que predice la teoría clásica).

La explicación es que, en las atmósferas de secuencia principal, las líneas se ensanchan adicionalmente por ensanchamiento de presión, lo que también da un perfil de Lorentz, que generalmente es más amplio que, y sobreenmascara, la amortiguación de radiación. (Las presiones en las atmósferas extendidas de gigantes y supergigantes son generalmente mucho menores que en las estrellas de secuencia principal, y en consecuencia las líneas son más estrechas). Volvemos al ensanchamiento de presión en una sección posterior.