10.4: Combinación de Perfiles

Varios factores de ensanchamiento pueden estar presentes simultáneamente en una línea. Dos mecanismos pueden tener perfiles similares (por ejemplo, ensanchamiento térmico y microturbulencia) o pueden tener perfiles muy diferentes (por ejemplo, ensanchamiento térmico y amortiguación de radiación). Necesitamos conocer el perfil resultante cuando hay más de un agente ensanchador presente. Consideremos una línea de emisión, y vamos\(x = \lambda - \lambda_0\). Supongamos que las líneas se ensanchan, por ejemplo, por ensanchamiento térmico, siendo la función de ensanchamiento térmico\(f(x)\). Supongamos, sin embargo, que, además, las líneas también se ensanchan por amortiguación de radiación, siendo el perfil de amortiguación de radiación\(g(x)\). A una\(ξ\) distancia del centro de la línea, la contribución al perfil de línea es la altura de la función\(f(ξ)\) ponderada por la función\(g(x - ξ)\). Es decir, el perfil resultante\(h(x)\) viene dado por

\[\label{10.5.1}h(x)=\int_{-\infty}^\infty f(ξ)g(x-ξ)\,dξ.\]

El lector debería convencerlo de que esto es exactamente lo mismo que

\[\label{10.5.2}h(x)=\int_{-\infty}^\infty f(x-ξ)g(ξ)\,dξ.\]

Este perfil se llama la convolución de los dos perfiles constituyentes, y a menudo se escribe simbólicamente

\[\label{10.5.3}h=f\ast g .\]

Convolución de dos funciones gaussianas

Consideremos, por ejemplo, la convolución de dos funciones gaussianas, por ejemplo la convolución del ensanchamiento térmico y microturbulento.

Supongamos que una de las funciones gaussianas es

\[\label{10.5.4}G_1(x)=\frac{1}{g_1}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left (-\frac{x^2\ln 2}{g_1^2}\right )=\frac{0.46972}{g_1}\text{exp}\left (-\frac{0.69315x^2}{g_1^2}\right ).\]

Aquí\(x=\lambda -\lambda_0\). El área bajo la curva es la unidad, el HWHM es\(g_1\) y el pico es\(\frac{1}{g_1}\sqrt{\frac{\ln 2}{\pi}}\). (Verifica estos.) Supongamos que la segunda función gaussiana es

\[\label{10.5.5}G_2(x)=\frac{1}{g_2}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left ( -\frac{x^2\ln 2}{g_2^2}\right).\]

Ahora se puede mostrar, usando la ecuación\ ref {10.5.1} o\ ref {10.5.2}, que la convolución de\(G_1\text{ and }G_2\) es

\[\label{10.5.6}G(x)=G_1(x)\ast G_2(x)=\frac{1}{g}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left (-\frac{x^2\ln 2}{g^2}\right ),\]

donde

\[\label{10.5.7}g^2=g_1^2+g_2^2.\]

Usamos este resultado ya en la Sección 10.4 cuando, al agregar microturbulentos al ensanchamiento térmico, sustituimos\(\sqrt{V_\text{m}^2+ξ_\text{m}^2}\) por\(V_\text{m}\). En caso de que encuentre problemática la integración, la he hecho en un Apéndice de este Capítulo.

Convolving Dos Funciones Lorentzianas

Ahora consideremos la combinación de dos funciones lorentzianas. La amortiguación de radiación da lugar a un perfil lorentziano, y veremos más adelante que el ensanchamiento de la presión también puede dar lugar a un perfil lorentziano. Supongamos que los dos perfiles lorentzianos son

\[\label{10.5.8}L_1(x)=\frac{l_1}{\pi}\cdot\frac{1}{x^2+l_1^2}\]

y

\[\label{10.5.9}L_2(x)=\frac{l_2}{\pi}\cdot \frac{1}{x^2+l_2^2}.\]

Aquí\(x=\lambda -\lambda_0\). El área bajo la curva es la unidad, el HWHM es\(l_1\) y el pico es\(1/(\pi l)\). (Verifica estos.) Se puede demostrar que

\[\label{10.5.10}L(x)=L(x)\ast L_2(x)=\frac{1}{\pi}\cdot \frac{1}{x^2+l^2},\]

donde

\[\label{10.5.11}l=l_1+l_2.\]

Los detalles de la integración se encuentran en el Apéndice de este Capítulo.

Convolución de una función lorentziana con una función gaussiana

Veamos ahora la convolución de un perfil gaussiano con un perfil lorentziano; es decir, la convolución de

\[\label{10.5.12}G(x)=\frac{1}{g}\cdot \sqrt{\frac{\ln 2}{\pi}}\text{exp}\left ( -\frac{x^2\ln 2}{g}\right ) \]

con

\[\label{10.5.13}L(x)=\frac{1}{\pi}\cdot \frac{1}{x^2+l^2}.\]

Podemos encontrar la convolución ya sea de la Ecuación\ ref {10.5.1} o de la Ecuación\ ref {10.5.2}, y obtenemos cualquiera

\[\label{10.5.14}V(x)=\frac{1}{g}\sqrt{\frac{\ln 2}{\pi^3}}\int_{-\infty}^\infty \frac{\text{exp}\left ( -[(ξ-x)^2\ln 2]/g^2\right ) }{ξ^2+l^2}dξ\]

o

\[\label{10.5.15}V(x)=\frac{1}{g}\sqrt{\frac{\ln 2}{\pi^3}}\int_{-\infty}^\infty \frac{\text{exp}[-(ξ^2\ln 2)/g^2]}{(ξ-x)^2+l^2}\,dξ.\]

La expresión\ ref {10.5.14} o\ ref {10.5.15}, que es una convolución de un perfil gaussiano y uno lorentziano, se denomina perfil Voigt. (Un intento rudo de pronunciación sería algo así como Focht.)

Un parámetro útil para describir la “gaussness” o “lorentzness” de un perfil de Voigt podría ser

\[\label{10.5.16}k_G=\frac{g}{g+l},\]

que es 0 para un perfil lorentz puro y 1 para un perfil gaussiano puro. En la figura X.4 he dibujado perfiles de Voigt para\(k_G = 0.25, 0.5\text{ and }0.75\) (continuo, discontinuo y punteado, respectivamente). Los perfiles se normalizan para que todos tengan la misma área. Un buen ejercicio para aquellos que son más pacientes y competentes con las computadoras que yo sería dibujar 1001 perfiles Voigt, con\(k_G\) pasar de 0 a 1 en pasos de 0.001, quizás normalizados todos a la misma altura en lugar de a la misma área, y hacer una película de un perfil gaussiano transformándose gradualmente a una perfil lorentziano. ¡Avísame si tienes éxito!

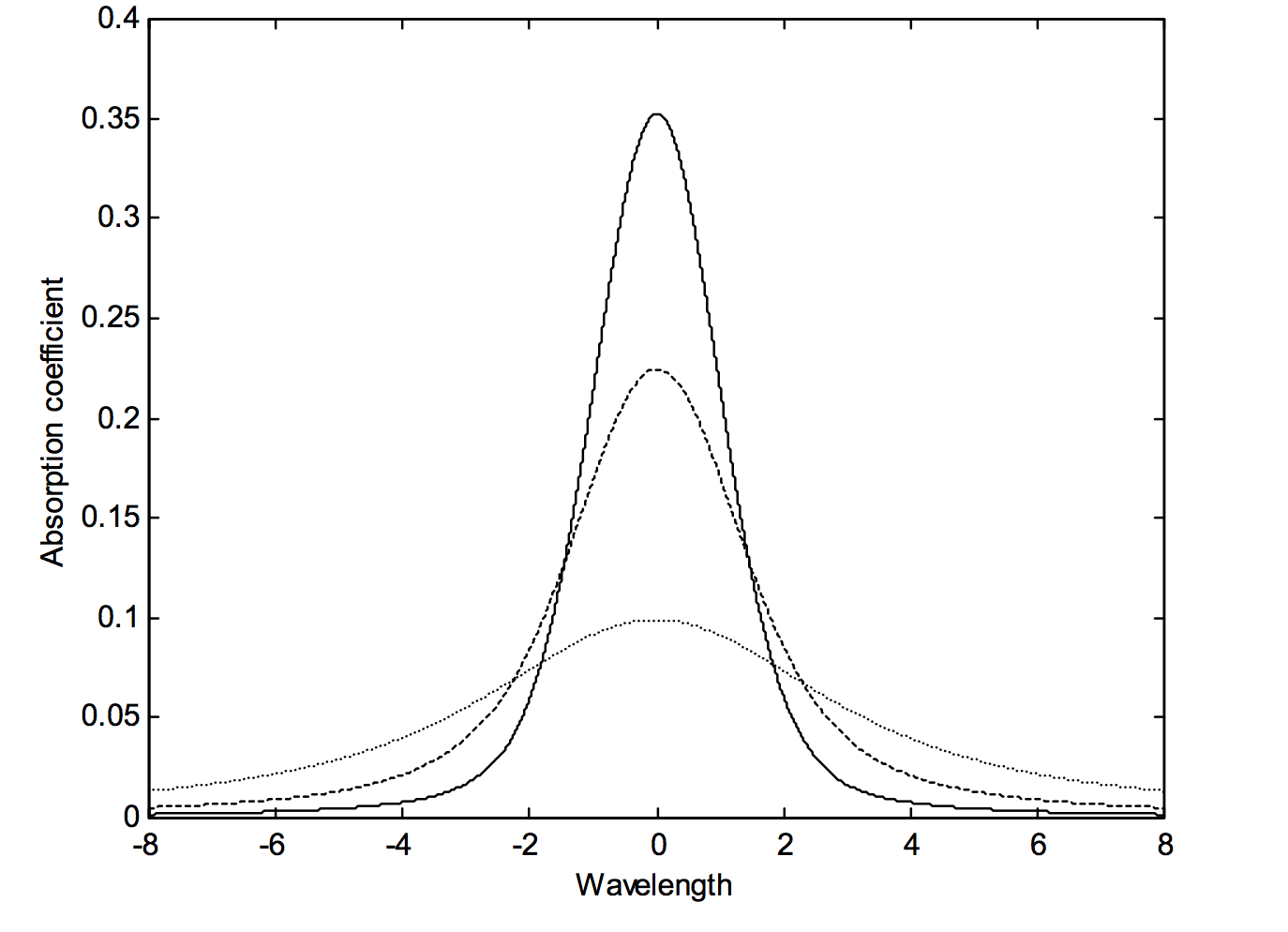
\(\text{FIGURE X.4}\)

En cuanto a los perfiles gauss-gauss y lorentz-lorentz, he anexado algunos detalles de la integración del perfil gauss-lorentz en el Apéndice de este Capítulo.

El FWHM o FWHM en unidades de longitud de onda de un perfil gaussiano (es decir\(2g\)) es

\[\label{10.5.17}w_G = \frac{\left ( 2kT/m +ξ_\text{m}^2\right )^{\frac{1}{2}}\lambda_0\sqrt{ln 16}}{c}=\frac{1.665 \left ( 2kT/m +ξ_\text{m}^2 \right )^{\frac{1}{2}}\lambda_0}{c}.\]

El FWHM o FWHM en unidades de frecuencia de un perfil lorentziano es

\[\label{10.5.18}w_L = \Gamma /(2\pi)=0.1592 \Gamma ,\]

Aquí\(\Gamma\) está la suma de la constante de amortiguación de radiación (ver sección 2) y la contribución del ensanchamiento de presión\(2 /\overline t\) (ver sección 6). Para el FWHM o FWHM en unidades de longitud de onda (i.e.\(2l\)), tenemos que multiplicar por\(\lambda_0^2 /c\).

Integración de un perfil Voigt

El área bajo perfil de Voigt es\(2\int_0^\infty V(x)\,dx\), donde\(V(x)\) viene dada por la Ecuación\ ref {10.5.14}, la cual a su vez tuvo que ser evaluada con una integración numérica. Dado que el perfil es simétrico aproximadamente\(x = 0\), podemos integrar desde\(0\text{ to }\infty\) y multiplicar por 2. Aun así, la doble integral podría parecer una tarea formidable. Particularmente problemático sería integrar un perfil casi lorentziano con alas extensas, porque entonces habría el problema de hasta dónde llegar para un límite superior. No obstante, no es para nada una tarea formidable. ¡El área bajo la curva dada por la Ecuación\ ref {10.5.14} es la unidad! Esto se ve fácilmente a partir de un ejemplo físico. El perfil dado por la Ecuación\ ref {10.5.14} es la convolución del perfil lorentziano de la Ecuación\ ref {10.5.13} con el perfil gaussiano de la Ecuación\ ref {10.5.12}, ambos normalizados al área unitaria. Imaginemos que una línea de emisión se ensancha por la amortiguación de la radiación, de manera que su perfil sea lorentziano. Ahora supongamos que se amplía aún más por ensanchamiento térmico (perfil gaussiano) para terminar como un perfil Voigt. (Alternativamente, supongamos que la línea es escaneada por un espectrofotómetro con una función de sensibilidad gaussiana). Claramente, siempre y cuando la línea sea siempre ópticamente delgada, el ensanchamiento adicional no afecta la intensidad integrada.

Ahora mencionamos en las secciones 2 y 3 de este capítulo que el ancho equivalente de una línea de absorción se puede calcular a partir de\(c \times\text{ central depth }\times\) FWHm, y de igual manera el área de una línea de emisión es\(c \times\text{ height }\times\) FWHM, donde\(c\text{ is }1.064 ( = \sqrt{\pi / \ln 16} )\) para un perfil gaussiano y\(1.571 (= \pi/2)\) para un perfil lorentziano. Sabemos que la integral de\(V(x)\) es la unidad, y es un asunto bastante sencillo calcular tanto la altura como el FWHM de\(V(x)\). A partir de esto, se hace posible calcular la constante\(c\) en función de la fracción gaussiana\(k_G\). El resultado de hacer esto se muestra en la figura X.4A.

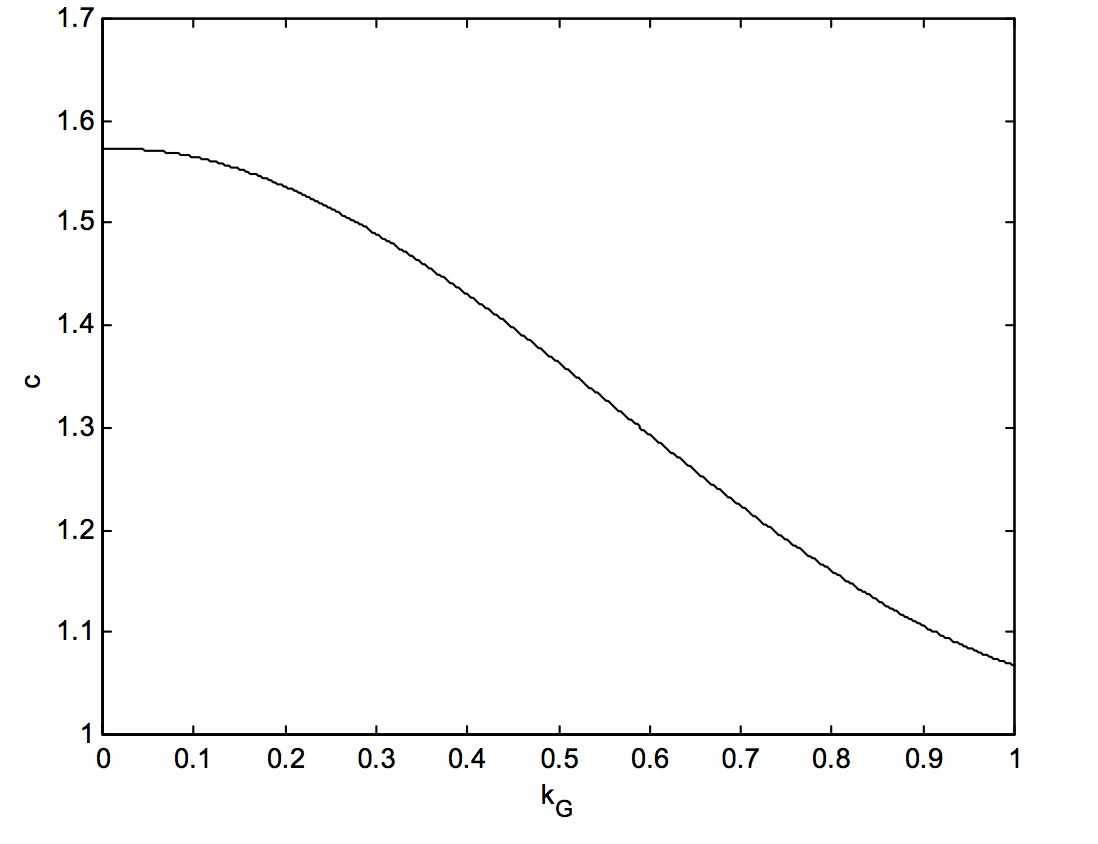
\(\text{FIGURE X.4A}\)

Esta curva se puede ajustar con la ecuación empírica

\[\label{10.5.19}c=a_0+a_1k_G+a_2k_G^2+a_3k_G^3,\]

donde\(a_0 = 1.572,\, a_1 = 0.05288,\, a_2 = -1.323\text{ and }a_3 = 0.7658\). El error incurrido al usar esta fórmula no supera en ninguna parte 0.5%; el error medio es 0.25%.

El Perfil Voigt en términos del Grosor Óptico en el Centro de Línea.

Otra forma de escribir el perfil de Voigt que podría ser útil es

\[\label{10.5.20}\tau (x) = Cl \tau (0) \int_{-\infty}^\infty \frac{\text{exp}[-(ξ-x)^2\ln 2/g^2]}{ξ^2+l^2}\,dξ .\]

Aquí\(x = \lambda - \lambda_0\) y\(ξ\) es una variable ficticio, que desaparece cuando se realiza la integral definida. El HWHM gaussiano es\(g=\lambda_0 V_\text{m} \sqrt{\ln 2}/c\), y el HWHM lorentziano lo es\(l=\lambda_0^2 \Gamma /(4\pi c)\). El espesor óptico en\(\lambda - \lambda_0 = x\) es\(\tau (x)\), y el espesor óptico en el centro de la línea es\(\tau (0)\). \(C\)es un coeficiente adimensional, cuyo valor depende de la fracción gaussiana\(k_G =g/(g+l)\). \(C\)está claramente dada por

\[\label{10.5.21}Cl \int_{-\infty}^\infty \frac{\text{exp}[-ξ^2\ln 2/g^2]}{ξ^2+l^2}\,dξ =1.\]

Si ahora dejamos\(l = l^\prime g / \sqrt{\ln 2}\) y\(ξ = ξ^\prime g / \sqrt{\ln 2}\), y también hacemos uso de la simetría del integrando sobre\(ξ = ξ^\prime = 0\), esto se convierte en

\[\label{10.5.22}2Cl^\prime \int_0^\infty \frac{\text{exp}\left ( -ξ^{\prime 2}\right ) }{ξ^{\prime 2}+l^{\prime 2}}dξ^\prime =1.\]

Al sustituir\(ξ^\prime =\frac{2l^\prime t}{1-t^2}\) (para que los límites sean finitos), obtenemos

\[\label{10.5.23}4C \int_0^1 \frac{\text{exp}[-\{2l^\prime t/(1-t^2)\}^2 ]}{1+t^2}\,dt =1,\]

que pueden integrarse fácilmente numéricamente para un valor dado de\(l^\prime\). Recordemos eso\(l/g=1/k_G -1\) y de ahí eso\(l^\prime = (1/k_G -1)\sqrt{\ln 2}\). Los resultados de la integración son los siguientes. La columna\(C_{\text{approx}}\) se explica siguiendo la figura X.4B.

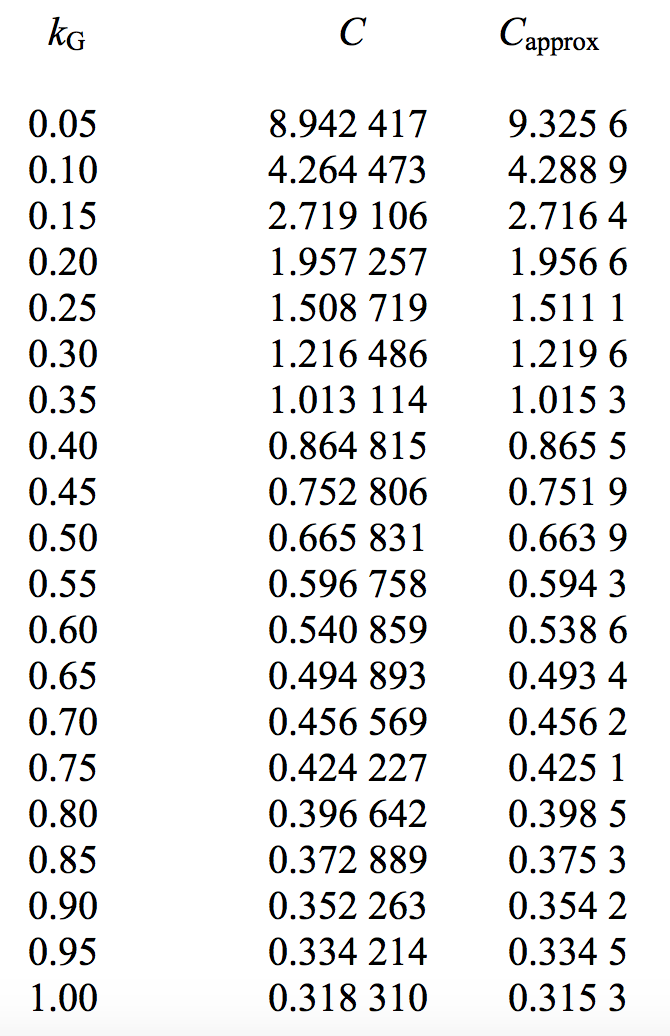
La última entrada, el valor de\(C\) for\(k_G = 1\), un perfil gaussiano puro, es\(1/\pi\). Estos datos se grafican en la figura X.4B.

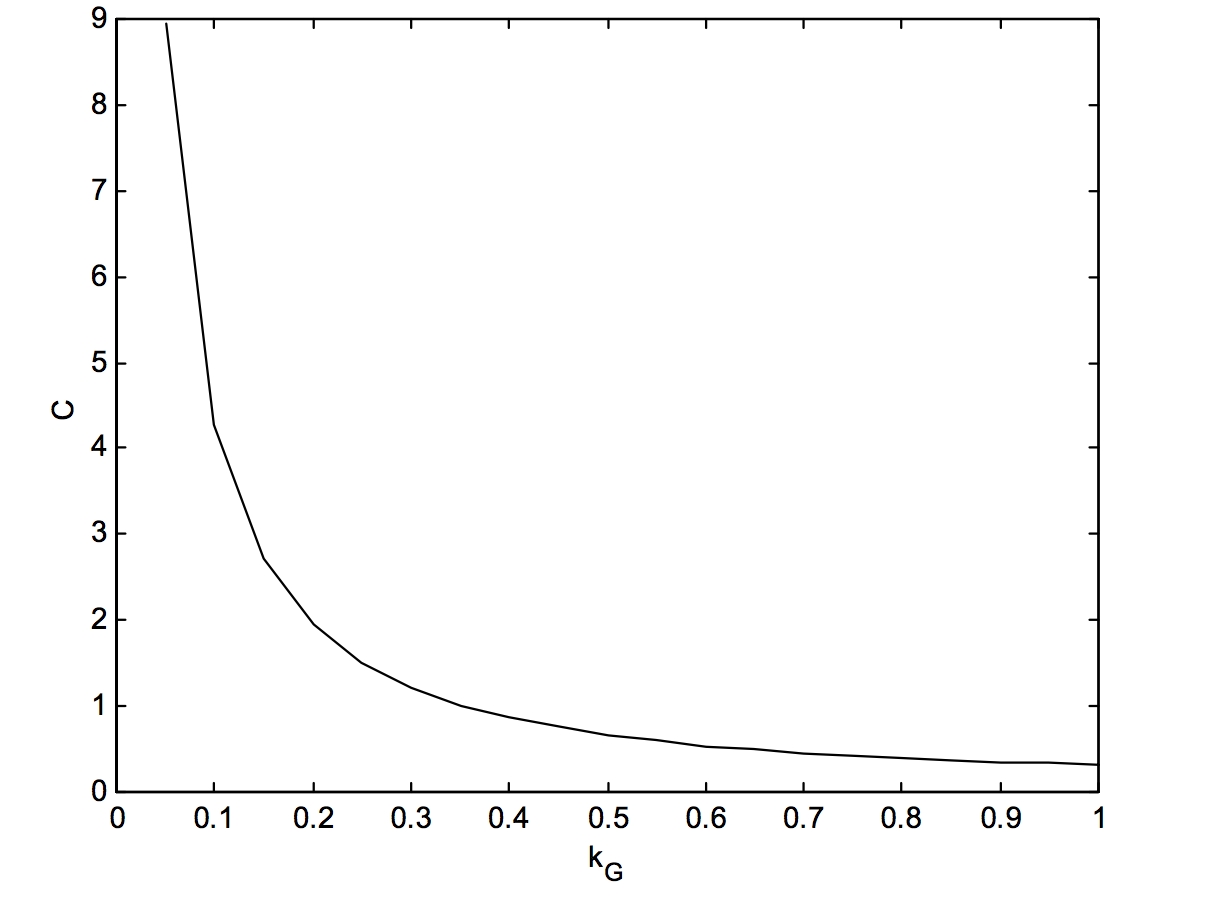
\(\text{FIGURE X.4B}\)

La fórmula empírica

\[\label{10.5.24}C_\text{approx}=ak_G^{-b}+c_0+c_1k_G+c_2k_G^2+c_3k_G^3,\]

donde

\[\nonumber\begin{align} &a=+0.309031 \quad &&b=+1.132747 \quad &&&c_0=+0.16510 \\ \nonumber&c_1=-0.82999 \quad &&c_2=+1.21782 \quad &&&c_3 =-0.54665 \\ \end{align}\]

ajusta la curva tolerablemente bien dentro (pero no fuera) del rango\(k_G = 0.15\text{ to }1.00\).