11.6: Curva de Crecimiento para Perfiles Voigt

Última actualización
Guardar como PDF

Page ID: 127385

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Nuestra siguiente tarea es construir curvas de crecimiento para perfiles de Voigt para diferentes valores de la relación de las HWHM lorentzianas y gaussianas\(l/g\), que es

\[\tag{11.6.1}\label{11.6.1}\frac{l}{g}=\frac{\Gamma \lambda_0}{4\pi V_\text{m}\sqrt{\ln 2}}=\frac{\Gamma \lambda_0}{V_\text{m}\pi \sqrt{\ln 65536}}=\frac{\Gamma \lambda_0}{34.841V_\text{m}},\]

o, mejor, para diferentes valores de la relación gaussiana\(k_G =\frac{g}{l+g}\). Estos deben parecer intermedios en apariencia entre las figuras XI.3 y 5.

La expresión para el ancho equivalente en unidades de longitud de onda viene dada por la Ecuación 11.3.4:

\[\tag{11.3.4}\label{11.3.4}W=2\int_0^\infty \left [ 1-\text{exp}\left \{ -\tau(x)\right \}\right ]\,dx.\]

combinado con la Ecuación 10.5.20

\[\tag{10.5.20}\label{10.5.20}\tau (x) = Cl \tau (0)\int_{-\infty}^\infty \frac{\text{exp}\left [ -(ξ-x)^2\ln 2/g^2\right ]}{ξ^2+l^2}\,dξ.\]

Es decir:

\[\tag{11.6.2}\label{11.6.2}W=2\int_0^\infty \left ( 1-\text{exp} \left \{ -Cl\tau(0)\int_{-\infty}^\infty \frac{\text{exp}\left [ -(ξ-x)^2\ln 2/g^2 \right ]}{ξ^2+l^2}dξ\right \}\right )\,dx.\]

Aquí

\(x = \lambda − \lambda_0\),\(l\) es el lorentziano\(\text{HWHM} = \lambda_0^2\Gamma/(4\pi c)\) (donde\(\Gamma\) puede incluir una contribución que amplía la presión),
\(g\)es el gaussiano\(\text{HWHM} = V_\text{m}\lambda_0\sqrt{\ln 2} / c\) (donde\(V_\text{m}\) puede incluir una contribución de microturbulencia), y
\(W\)es el ancho equivalente, todo de dimensión\(L\).

El símbolo\(ξ\), también de dimensión L, es una variable ficticio, que desaparece después de la integración definitiva. \(\tau(0)\)es el grosor óptico en el centro de la línea. \(C\)es un número adimensional dado por la Ecuación 10.5.23 y tabulado en función de la fracción gaussiana en el Capítulo 10. Se exhorta al lector a verificar cuidadosamente las dimensiones de la Ecuación\ ref {11.6.2}. La integración de la Ecuación\ ref {11.6.2} se discute en el Apéndice A.

Nuestro objetivo es calcular el ancho equivalente en función de\(\tau(0)\) para diferentes valores de la fracción gaussiana\(k_G = g/(l + g)\). Lo que encontramos es lo siguiente. Let\(W^\prime = W \sqrt{\ln 2 }/g\); es decir,\(W^\prime\) es el ancho equivalente expresado en unidades de\(g /\sqrt{ \ln 2}\). Por\(\tau(0)\) menos de aproximadamente 5, donde las alas aportan relativamente poco al ancho equivalente, encontramos que\(W^\prime\) es casi independiente de la fracción gaussiana. La diferencia en el comportamiento de la curva de crecimiento para diferentes perfiles aparece sólo para grandes valores de\(\tau (0)\), cuando las alas asumen un papel mayor. Sin embargo, para cualquier perfil que sea menos gaussiano que aproximadamente\(k_G\) igual a aproximadamente 0.9, el comportamiento de la curva de crecimiento (for\(\tau(0) > 5\)) imita al de un perfil lorentziano. Por esa razón he dibujado curvas de crecimiento en la figura XI.6 sólo para\(k_G = 0.9, 0.99, 0.999\text{ and }1\). Esto corresponde a\(l/g = 0.1111, 0.0101, 0.0010\text{ and }0\), o a\(\Gamma \lambda_0 /V_m = 1.162, 0.1057, 0.0105\text{ and }0\) respectivamente.

alt
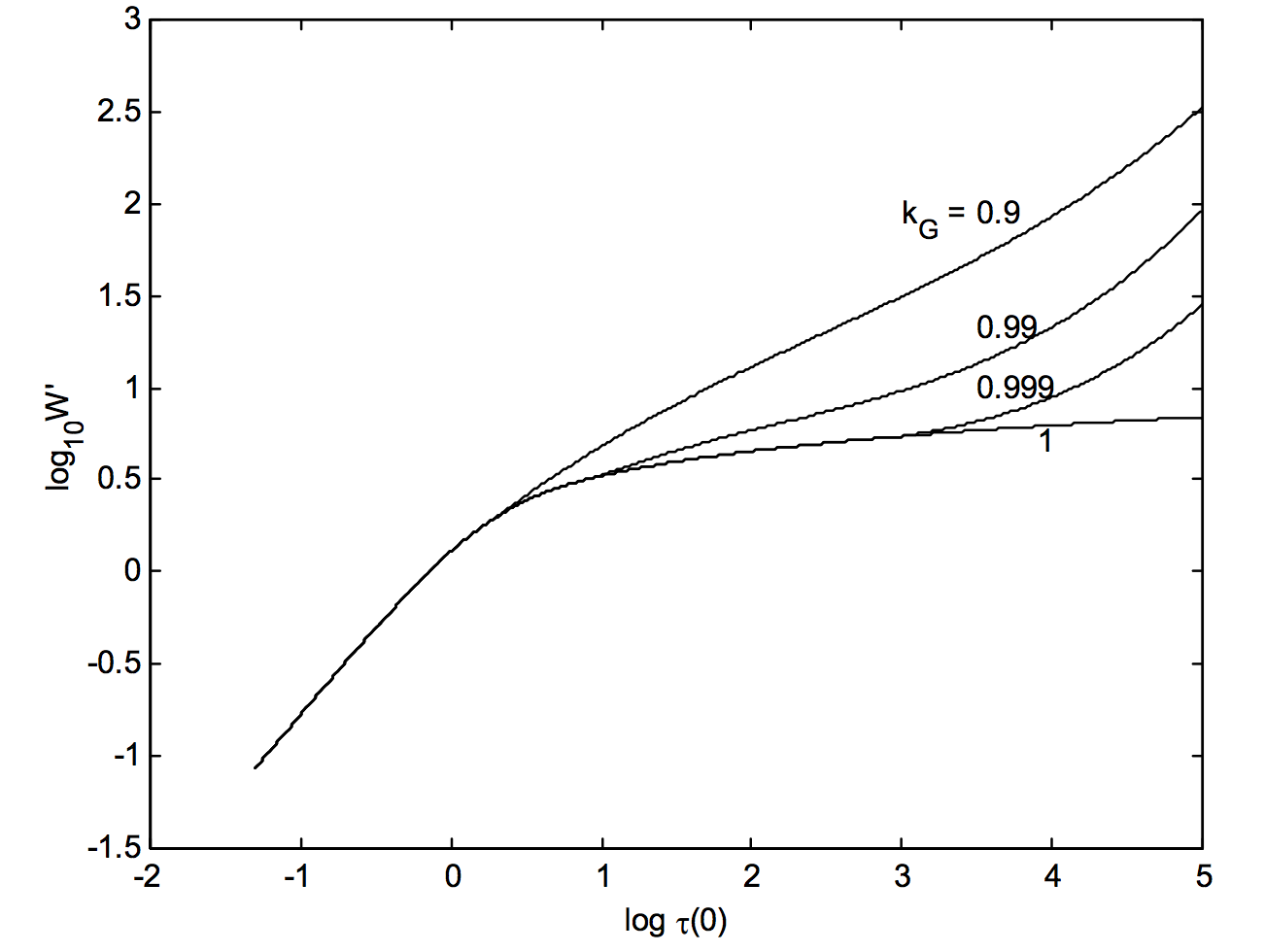
\(\text{FIGURE XI.6}\)