11.9: APÉNDICE A- Evaluación de la Curva Voigt de Crecimiento Integral

Deseamos evaluar el ancho equivalente dado por la ecuación 11.6.2:

\[\tag{11.A.1}W=2\int_0^\infty \left ( 1-\text{exp}\left \{-Cl\tau(0)\int_{-\infty}^\infty \frac{\text{exp}[-(ξ-x)^2\ln 2/g^2]}{ξ^2+l^2}dξ\right \} \right ) dx.\]

Lo simplificamos ligeramente introduciendo variables adimensionales\(W^\prime,\, x^\prime,\, ξ^\prime \text{ and }l^\prime\) definidas por\(X^\prime = \frac{Xc}{\lambda_0V_m}=\frac{X\sqrt{\ln 2}}{g}\), donde\(X\) está cualquiera de\(W,\, x,\, ξ\text{ or }l\). Es decir, estamos expresando longitudes en unidades de\(g /\sqrt{\ln 2}\). Entonces:

\[\tag{11.A.2}W^\prime = 2\int_0^\infty \left ( 1-\text{exp}\left \{ -Cl^\prime \tau(0)\int_{-\infty}^\infty \frac{\text{exp}[-(ξ^\prime -x^\prime)^2]}{ξ^{\prime 2}+l^{\prime 2}}dξ^\prime \right \} \right )dx^\prime .\]

Eventualmente vamos a querer evaluar la integral como una función de la relación gaussiana\(k_G\), y lo notamos\(l^\prime = \left ( \frac{1}{k_G}-1\right ) \sqrt{\ln 2}\). Dado que\(ξ^\prime\) es una variable ficticio, en principio podríamos prescindir del prime como superfluo, pero probablemente sea útil retener el prime. Los límites de la integral interna pueden hacerse finitos por medio de un cambio de variable. La sustitución\(ξ^\prime = l^\prime \tan \theta\) logrará esto, pero la introducción de una función trigonométrica incrementará el tiempo de cómputo. Una alternativa es\(ξ^\prime =\frac{2l^\prime t}{1-t^2}\), que parece más torpe pero es bastante más rápida. La ecuación se convierte

\[\tag{11.A.3}W^\prime =2\int_0^\infty \left ( 1-\text{exp}\left \{-2C\tau(0)\int_{-1}^1 \frac{\text{exp}[-(\frac{2l^\prime t}{1-t^2}-x^\prime )^2]}{1+t^2}dt\right \} \right )dx^\prime.\]

Esta integral no es particularmente fácil, y no aconsejo simplemente ponerla en un programa de integración preempaquetado sin un examen crítico. (¡De hecho nunca lo defiendo!) Uno se enfrenta a los habituales problemas de integración numérica: ¿Cuál debería ser el tamaño del paso y el número de pasos? Y, en el caso de la integral externa, ¿hasta dónde debemos llevar el límite superior? Una forma de determinar el número necesario de intervalos (y el tamaño del paso) es intentar, digamos 100 intervalos, y luego probar 1000, y ver si hace alguna diferencia. De igual manera con la determinación del límite superior a la integración externa, intente integrar a\(x^\prime = 5\), y luego a 10, y vea si hace alguna diferencia. Pero esta integral tiene algunos problemas propios.

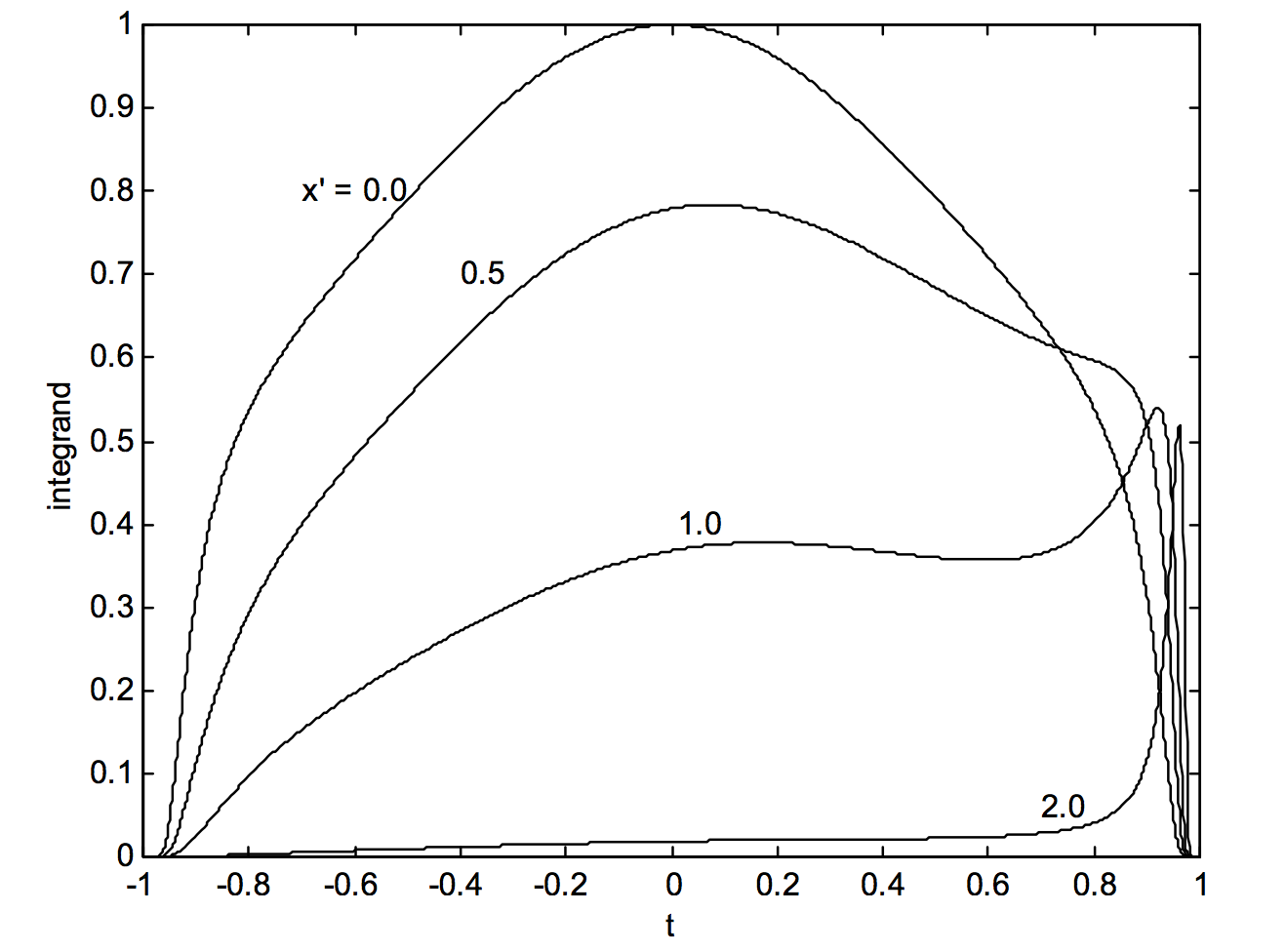
Se puede obtener cierta información sobre los problemas observando el comportamiento del integrando interno. Esta función,\(\frac{\text{exp}[-(\frac{2l^\prime t}{1-t^2}-x^\prime)^2]}{1+t^2}\), se muestra como una función de\(t\) para cuatro valores diferentes de\(x^\prime\) en la figura XI.A1 El valor de\(l^\prime\) para la figura es\(1/(4\pi)\), que no tiene significación particular, ya que la figura está destinada únicamente a fines ilustrativos.

Para\(x^\prime = 0\), la función es simétrica sobre\(t = 0\), pero no para otros valores de\(x^\prime\). Para valores pequeños de x', no hay ninguna dificultad particular con la integración, ya sea por la regla de Simpson o por la integración de siete puntos (ver mis notas web sobre Mecánica Celestial, Capítulo 1).

\(\text{FIGURE XI.A1}\)

Sin embargo, para grandes\(x^\prime\), el integrando está cerca de cero para la mayor parte del rango entre\(t = -1.0\text{ and }0.0\), pero, cerca de\(t = 1.0\), el integrando exhibe un pico agudo, convirtiéndose casi en una función delta para mayores\(x^\prime\). Un intervalo aproximado para la integración puede perder el pico por completo, mientras que un intervalo muy fino utilizará cantidades masivas de tiempo de computadora sin un buen propósito en la mayor parte del rango de\(t\). Afortunadamente, el área bajo el pico es progresivamente cada vez más pequeña para cada vez más grandes\(x^\prime\) pero la pregunta fastidiosa aún permanece, ¿cuándo puede uno dejar de integrarse? Una técnica útil, eficiente y efectiva es ajustar el tamaño del intervalo para la integración de acuerdo a la pendiente de la función. Un intervalo grueso es bastante adecuado mientras que la gráfica es casi horizontal, pero un paso de integración mucho más fino se inicia tan pronto como la pendiente se vuelve grande. Esto requiere cierta cantidad de programación legerdemain, pero con frecuencia se recurre a ello en este tipo de situaciones.

La parte de la ecuación 11.A 2:

\[\tag{11.A.4}\text{exp}\left \{ -Cl\tau(0)\int_{-\infty}^\infty \frac{\text{exp}[-(ξ-x)^2\ln 2/g^2]}{ξ^2+l^2}dξ\right \}\]

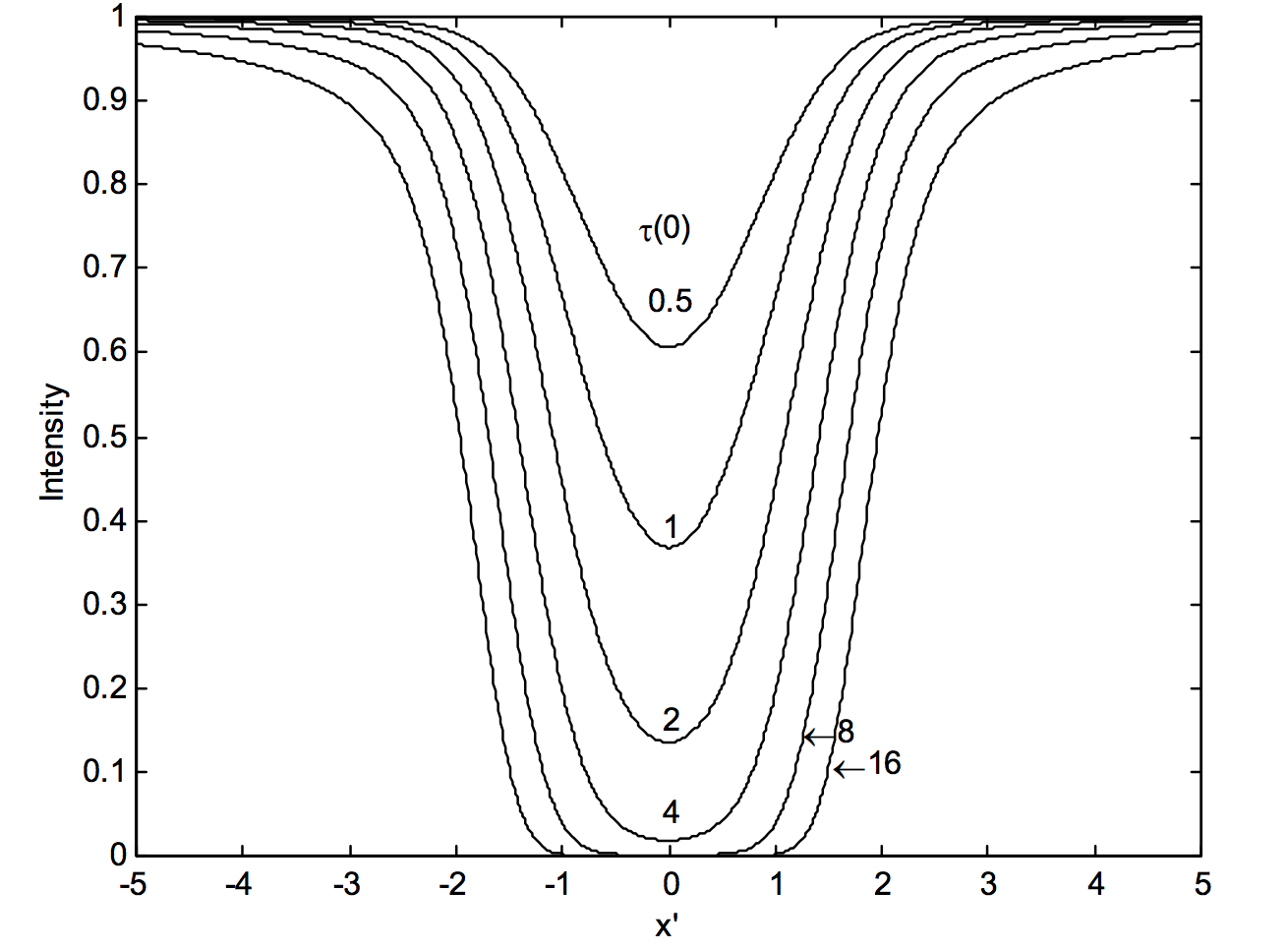
representa el perfil Voigt ópticamente grueso. Esto se muestra\(l^\prime = 1/(4\pi)\) para varios\(\tau(0)\) en la figura XI.A.2. El valor no\(l^\prime = 1/(4\pi)\) tiene significación particular; la figura XI.A.2 se dibujó únicamente con fines ilustrativos.

\(\text{FIGURE XI.A2}\)

El ancho equivalente (ecuación 11.A.1) es el área por encima de estas curvas, y se puede ver de nuevo que determinar el límite superior para\(x^\prime\) es un problema.

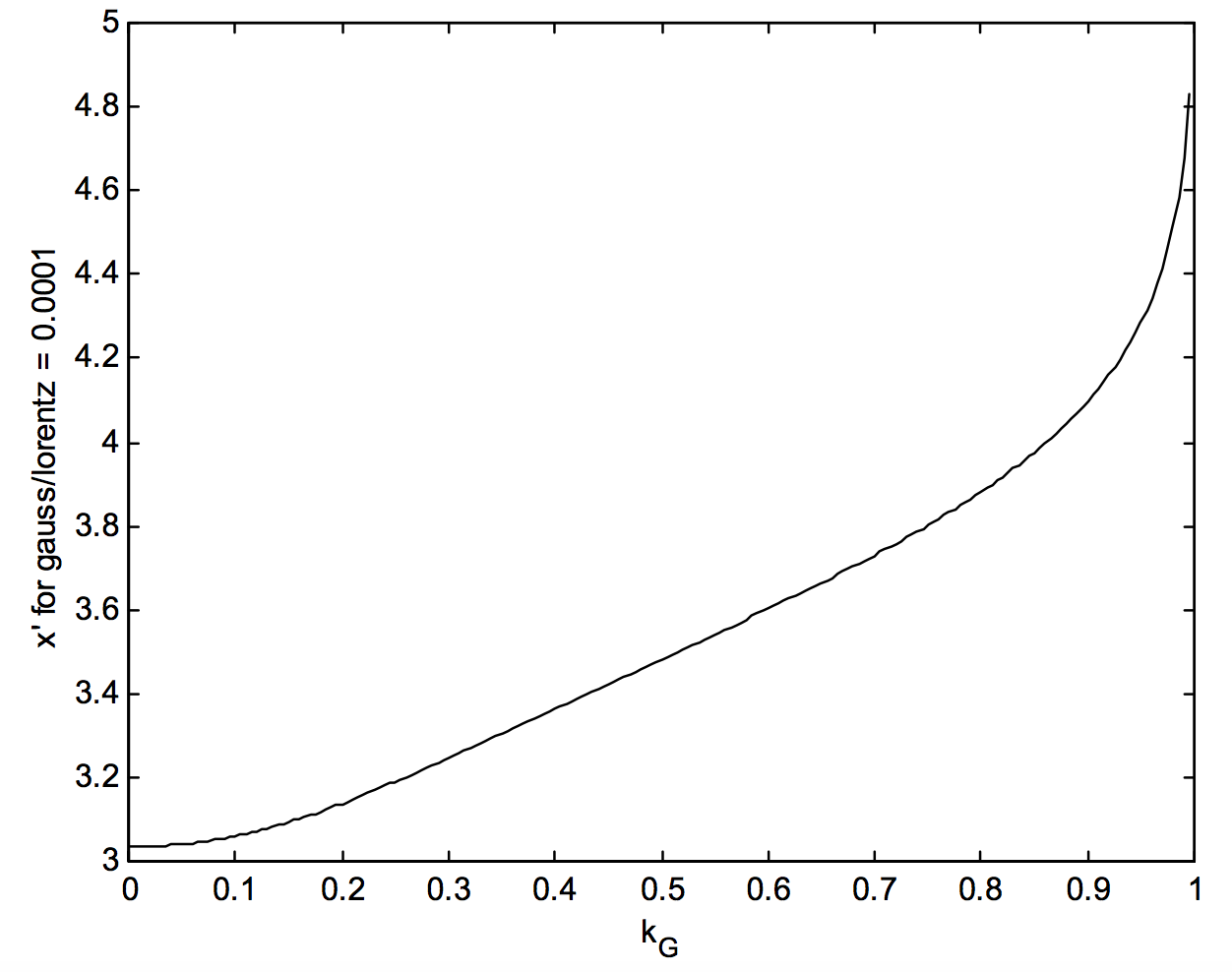
Podemos, sin embargo, recordar que el perfil que estamos integrando es la convolución de un gaussiano y un lorentziano, y eso\(x^\prime\text{ is }\lambda - \lambda_0\) en unidades de\(2g /\sqrt{\ln 2}\). El componente gaussiano tiene alas muy pequeñas, mientras que el perfil lorentziano tiene alas extensas. La relación del componente gaussiano a la ordenada al componente lorentziano es\(\left ( \frac{l^{\prime 2}+x^{\prime 2}}{l^{\prime 2}}\right )\text{exp}(-x^{\prime 2})\), donde\(l^\prime = (1/k_G-1)\sqrt{\ln 2}\). El valor\(x^\prime\) en el que esta relación cae a 0.0001 se muestra como una función de\(k_G\) en la figura XI.a.1a. Más allá de este punto se pueden tratar las alas del perfil como lorentzianas.

Así, la ecuación 11.A.2 puede integrarse tratando el perfil ópticamente delgado como una función Voigt hasta algunos\(x^\prime = a\) y como una función lorentziana posteriormente. Es decir, he escrito la ecuación 11.A.2 como

\(\text{FIGURE XI.A.1A}\)

\[\begin{align}W^\prime = 2&\int_0^a \left ( 1-\text{exp}\left \{-Cl^\prime \tau(0)\int_{-\infty}^\infty \frac{\text{exp}[-(ξ^\prime -x^\prime)^2]}{ξ^{\prime 2}+l^{\prime 2}}dξ^\prime \right \} \right )dx^\prime \\ &+2\int_a^\infty \left (1-\text{exp}\left \{-\frac{\tau(0)}{x^{\prime 2}+l^{\prime 2}}\right\} \right )dx^\prime .\\ \tag{11.A.5}\end{align}\]

Al sustituir\(ξ^\prime = \frac{2l^\prime t}{1-t^2}\) en la primera integral y\(x^\prime = l^\prime \tan \theta\) en la segunda, esto se convierte

\[\begin{align} W^\prime = 2&\int_0^a \left ( 1-\text{exp}\left \{ -2C\tau(0)\int_{-1}^1 \frac{\text{exp}[-(\frac{2l^\prime t}{1-t^2}-x^\prime )^2 ]}{1+t^2}dt\right \} \right ) dx^\prime \\ &+2l^\prime \int_\alpha^{\pi/2} \frac{\left (1-\text{exp}\left \{ -\tau(0)\cos^2 \theta \right \}\right )}{\cos^2 \theta}d\theta, \\ \tag{11.A.6}\end{align}\]

donde\(\tan \alpha = l^\prime / a\). El temido símbolo ya se\(\infty\) ha ido y, además, no hay problema en el límite superior de la segunda integral, por el valor del integrando cuando\(\theta = \pi /2\) es unidad.