11.8: Interpretación de un Perfil Ópticamente Grueso

Última actualización
Guardar como PDF

Page ID: 127397

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Este capítulo se ha preocupado por las líneas ópticamente gruesas y con la curva de crecimiento —y cómo se podrían recuperar los parámetros\(g\) y\(l\) de la curva de crecimiento aunque no se resuelvan los perfiles de líneas individuales. Esta sección está escrita más bien como una idea de último momento, aunque importante, y no se refiere a la curva de crecimiento. Se discute cómo se podría analizar el perfil de una línea que está bien resuelta, pero que no es ópticamente delgada. Utilizo como ejemplo una línea que se ensancha térmicamente y que, de ser ópticamente delgada, tendría un perfil gaussiano. La línea ópticamente gruesa ya no es gaussiana, pero ¿se puede recuperar\(g\) (y por lo tanto\(T\)) de ella? Sólo para variar, y porque hace un tiempo desde que usamos el término “función fuente”, me ocuparé de una línea de emisión.

Como se discute en la Sección 5.7, el resplandor de una losa de gas de función fuente\(S\) viene dada por

\[\label{11.8.1}I_\lambda (x)=S\int_0^{\tau(x)}e^{-\tau}\,d\tau = S(1-e^{-\tau(x)}).\]

Aquí,\(x=\lambda - \lambda_0\). Para una línea térmicamente ampliada, esto se convierte en

\[\label{11.8.2}I_\lambda (x)=S\left [ 1-\text{exp}\left \{ -\tau (0) \text{exp}(-x^2 \ln 2/g^2 )\right \} \right ] ,\]

donde\(g=V_m \lambda_0/ \sqrt{\ln 2}.\)

En la figura XI.7, dibujo dos de esos perfiles, en los que la fuerza de línea de uno es\(A\) multiplicada por la resistencia de la línea del otro. Las líneas, tal vez, pertenecen al mismo multiplete y se conoce la relación de las fortalezas de línea. (Estoy aquí usando el término fuerza de línea en el sentido técnico del Capítulo 7.) La Figura XI.7 se dibujó con\(A = 2\), pero como las líneas no son ópticamente delgadas, ni la relación de sus áreas ni la relación de sus alturas es de dos.

alt
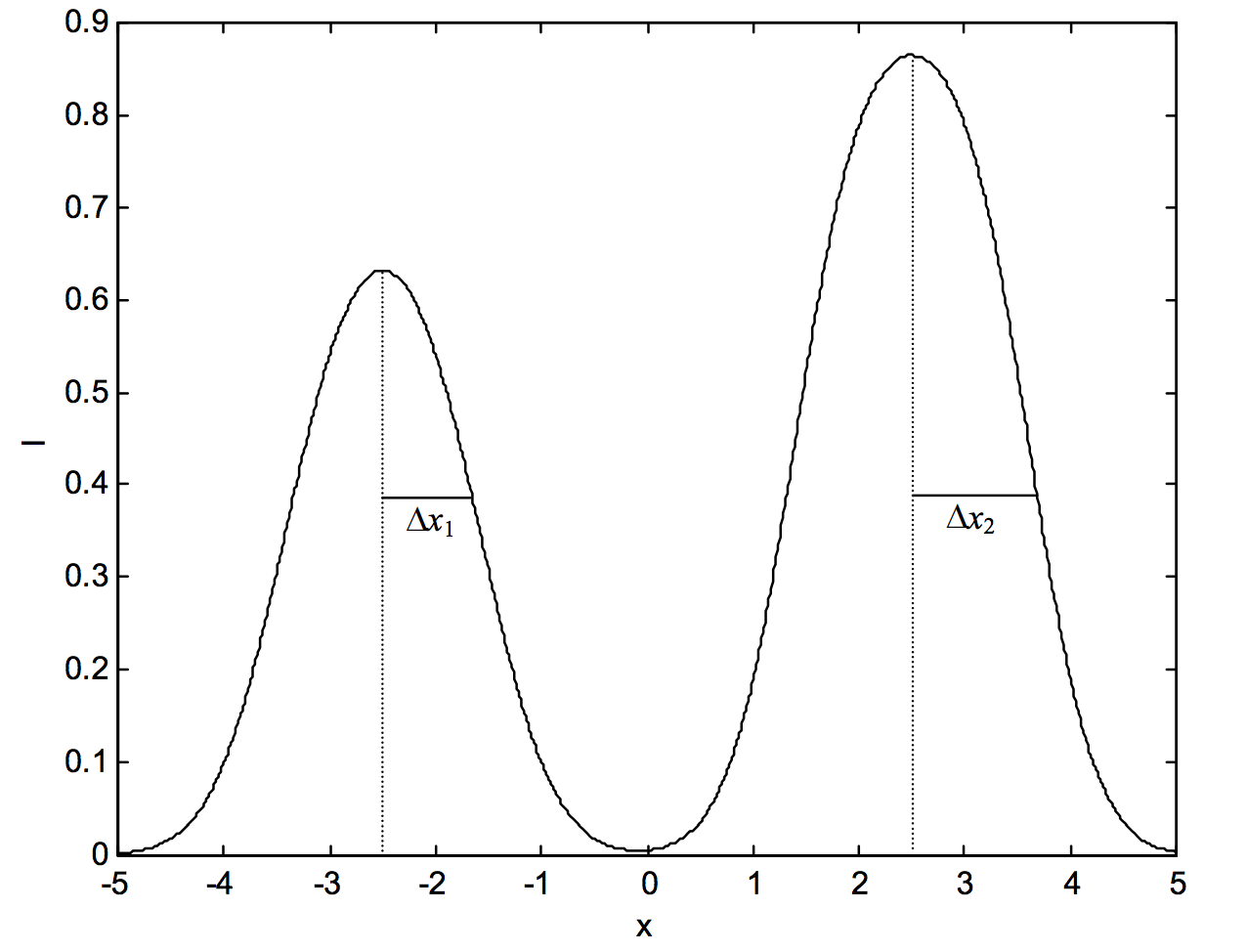
\(\text{FIGURE XI.7}\)

Podemos medir las medias anchuras\(\Delta x_1\text{ and }\Delta x_2\) de los dos perfiles a la misma altura.

Entonces:

\[\label{11.8.3}S[1-\text{exp}\{-\tau(0)\text{exp}(-(\Delta x_1)^2\ln 2/g^2)\}]=S[1-\text{exp}\{-A\tau(0)\text{exp}(-(\Delta x_2)^2\ln 2/g^2)\}],\]

después de lo cual

\[\label{11.8.4}\frac{(\Delta x_1)\ln 2}{g^2}=\frac{(\Delta x_2)\ln 2}{g^2}-\ln A,\]

y por lo tanto

\[\label{11.8.5}g^2=\frac{[(\Delta x_1)^2-(\Delta x_2)^2]}{\ln A}.\]

La misma técnica se puede utilizar para perfiles lorentzianos.