5.4.6: Varillas

Última actualización
Guardar como PDF

Page ID: 131495

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

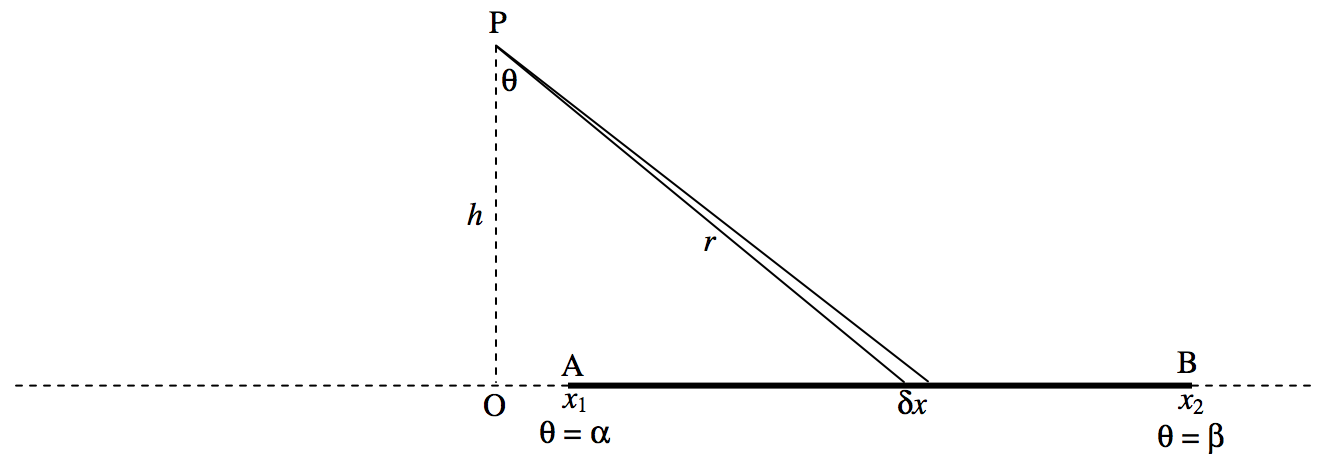
Figura 5.5.png
\(\text{FIGURE V.5}\)

Considera la varilla que se muestra en la figura\(\text{V.5}\), de masa por unidad de longitud\(λ\). El campo en\(\text{P}\) debido al elemento\(δx\) es\(Gλ δx/r^2\). Pero\(x = \tan θ\),\(δx = h \sec^2 θδθ\),\(r = h \sec θ\) entonces el campo en\(\text{P}\) es\(Gλ δθ / h\) Esto va dirigido desde\(\text{P}\) al elemento\(δx\).

El\(x\) -componente del campo debido a toda la varilla es

\[\frac{Gλ}{h} \int_α^β \sin θ \ dθ = \frac{Gλ}{h} ( \cos α - \cos β ). \label{5.4.15} \tag{5.4.15}\]

El\(y\) -componente del campo debido a toda la varilla es

\[-\frac{Gλ}{h} \int_α^β \cos θ \ dθ = -\frac{Gλ}{h} ( \sin β - \sin α). \label{5.4.16} \tag{5.4.16}\]

El campo total es la suma ortogonal de estos, que, tras el uso de algunas identidades trigonométricas (¡hazlo!) , se convierte

\[g = \frac{2Gλ}{h} \sin \frac{1}{2} (β - α) \label{5.4.17} \tag{5.4.17}\]

en un ángulo\(\frac{1}{2} (α + β)\), es decir, bisectando el ángulo\(\text{APB}\).

Si la varilla es de longitud infinita, ponemos\(α = − \pi/2\) y\(β = \pi /2\), y obtenemos para el campo en\(\text{P}\)

\[g = \frac{2Gλ}{h}. \label{5.4.18} \tag{5.4.18}\]

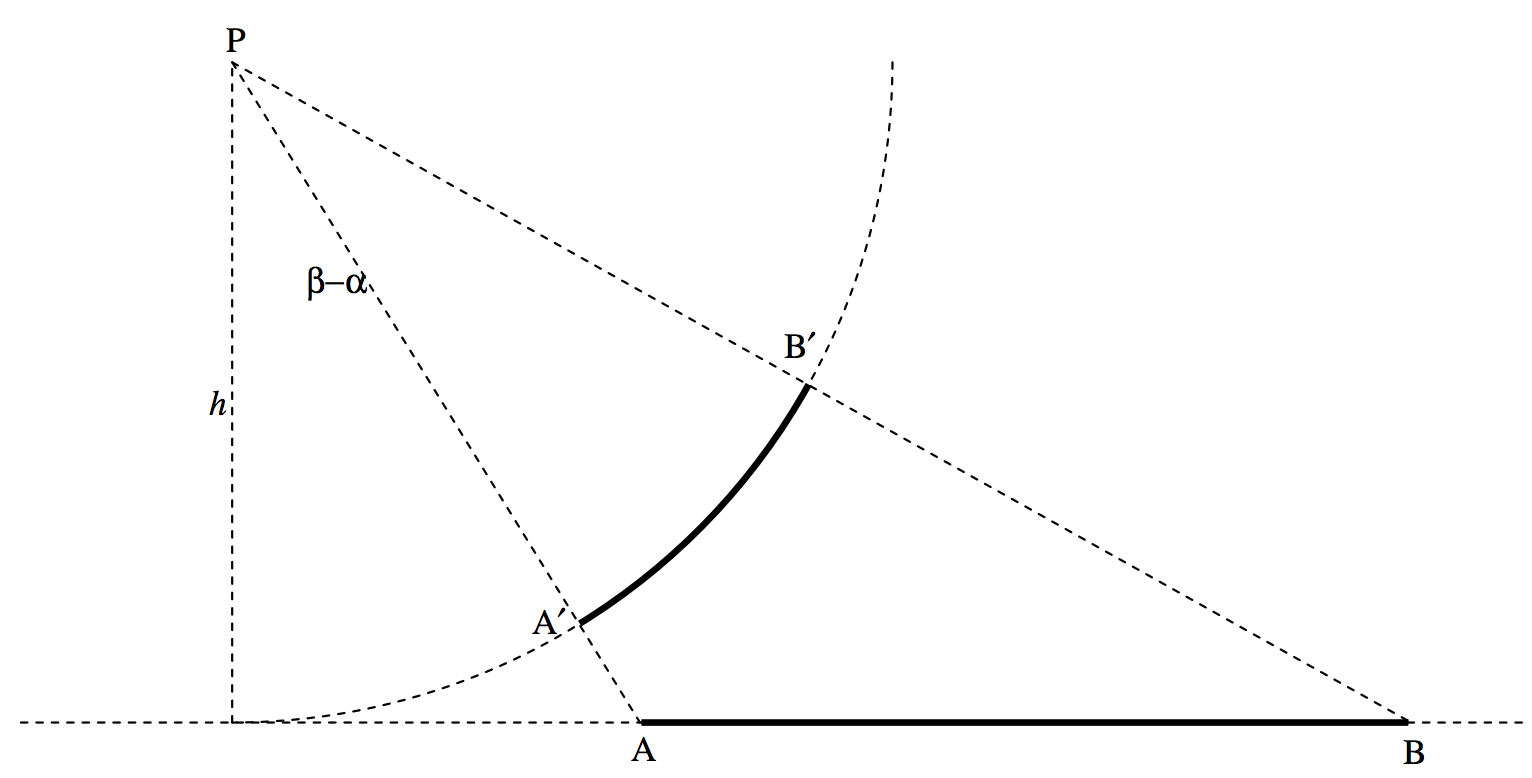
Figura 5.6.png
\(text{FIGURE V.6}\)

Considera un arco\(\text{A}^\prime \text{B}^\prime\) de círculo de radio\(h\), masa por unidad de longitud\(λ\), subtendiendo un\(β−α\) ángulo en el centro\(\text{P}\) del círculo.

Ejercicio: Demostrar que el campo en\(\text{P}\) es\(g = \frac{2Gλ}{h} \sin \frac{1}{2}(β−α)\). Esto es lo mismo que el campo debido a que la varilla\(\text{AB}\) subtiende el mismo ángulo. Si\(\text{A}^\prime \text{B}^\prime\) es un semicírculo, el campo at\(\text{P}\) sería\(g = \frac{2Gλ}{h}\), lo mismo que para una varilla infinita.

Un resultado interesante que se desprende de esto es el siguiente.

\(\text{FIGURE V.7}\)

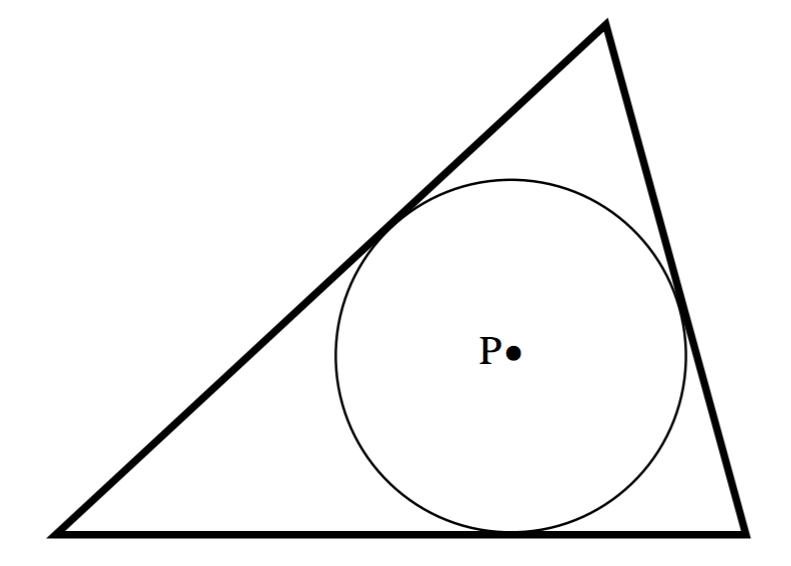
Figura 5.7.png

Tres varillas macizas forman un triángulo. \(\text{P}\)es el incentro del triángulo (es decir, es equidistante de los tres lados). El campo at\(\text{P}\) es el mismo que el que se obtendría si la masa se distribuyera alrededor del círculo. Es decir, es cero. El mismo resultado se sostendría para cualquier cuadrilátero que se pueda inscribir con un círculo —como un cuadrilátero cíclico.