5.4.7: Cilindro Sólido

Última actualización
Guardar como PDF

Page ID: 131470

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

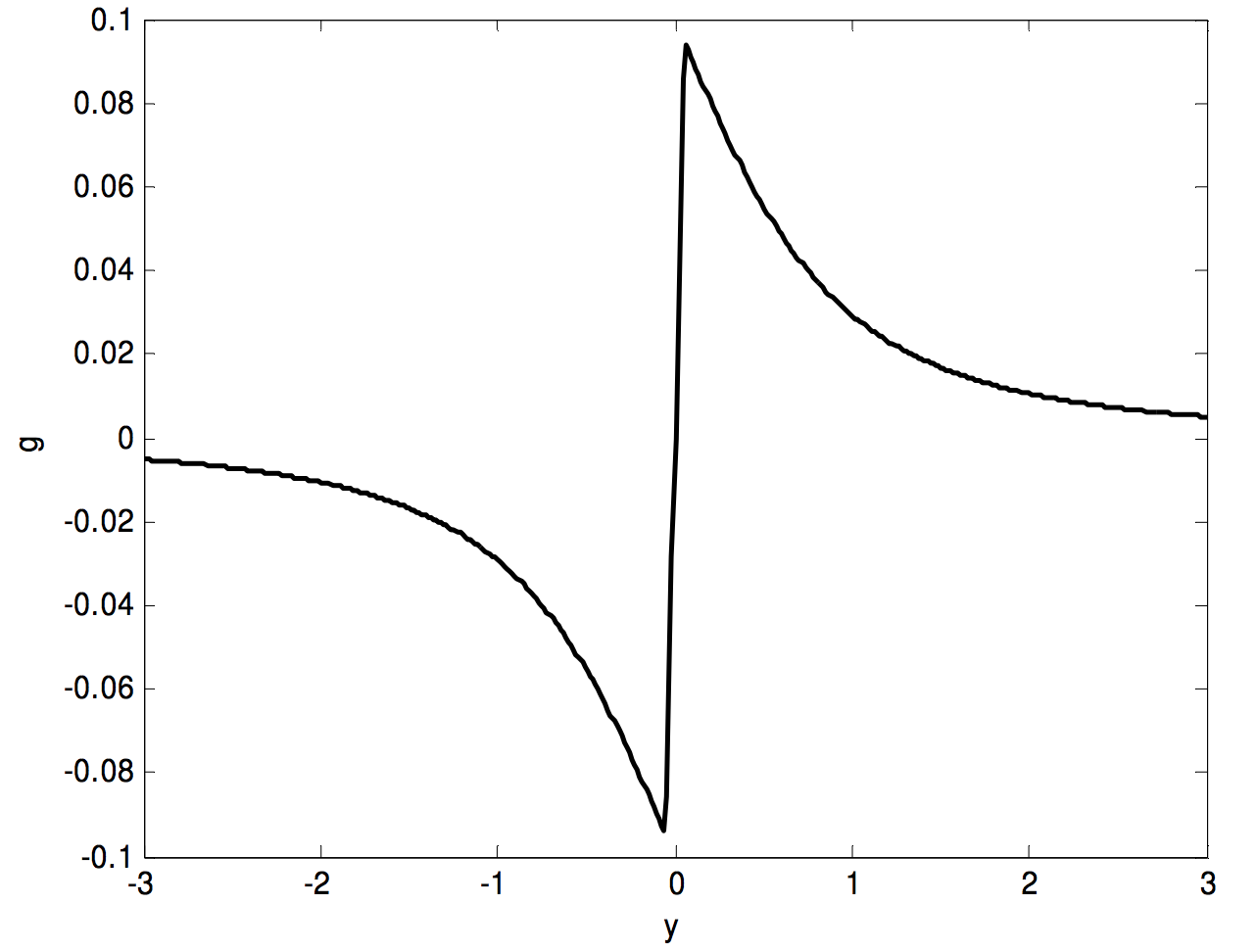
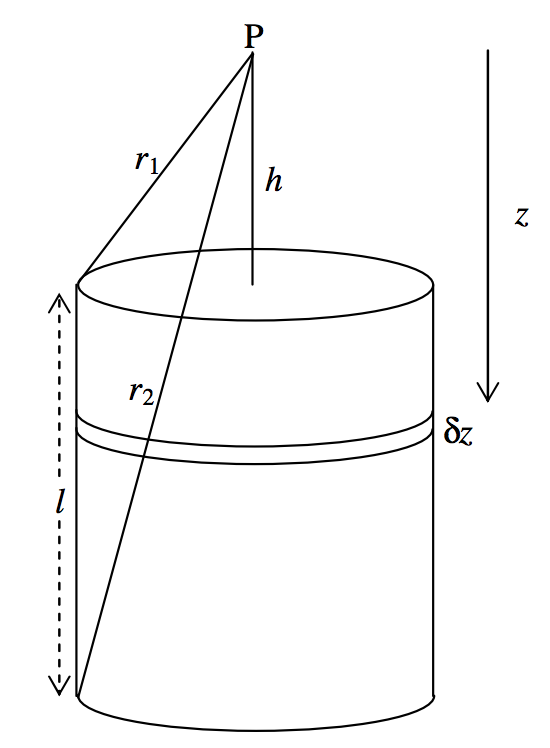
Esto lo hacemos no porque tenga alguna relevancia particular para la mecánica celeste, sino porque es fácil de hacer. Imaginamos un cilindro sólido, densidad\(ρ\), radio\(a\), longitud\(l\). Buscamos calcular el campo en un punto\(\text{P}\) del eje, a una distancia\(h\) de un extremo del cilindro (figura\(\text{V.8}\)).

Figura 5.8.png
\(\text{FIGURE V.8}\)

El campo a\(\text{P}\) partir de un disco elemental de espesor\(δz\) una distancia z por debajo de P es (de la Ecuación 5.4.9)

\[δg = Gρδzω. \label{5.4.19} \tag{5.4.19}\]

Aquí\(ω\) está el ángulo sólido subtendido\(\text{P}\) por el disco, que es\(2 \pi \left[ 1 - \frac{z}{\left( z^2 + a^2 \right)^{1/2}} \right]\). Por lo tanto, el campo en\(\text{P}\) de todo el cilindro es

\[g = 2 \pi G ρ \int_h^{l+h} \left[ 1 - \frac{z}{(z^2 + a^2)^{1/2}} \right] dz, \label{5.4.20} \tag{5.4.20}\]

o\[g = 2 \pi G ρ \left( l - \sqrt{(l+h)^2 + a^2} + \sqrt{h^2+ a^2} \right), \label{5.4.21} \tag{5.4.21}\]

o\[g = 2\pi G ρ ( l - r_2 + r_1 ). \label{5.4.22} \tag{5.4.22}\]

También podría ser de interés expresarse\(g\) en términos de la altura\(y (= \frac{1}{2}l + h)\) del punto\(\text{P}\) por encima del punto medio del cilindro. En lugar de Ecuación\(\ref{5.4.21}\), entonces tenemos

\[g = 2 \pi G ρ \left( l - \sqrt{(y + \frac{1}{2}l)^2 + a^2} + \sqrt{(y - \frac{1}{2}l)^2 + a^2} \right) . \label{5.4.23} \tag{5.4.23}\]

Si el punto\(\text{P}\) está dentro del cilindro, a una distancia\(h\) por debajo del extremo superior del cilindro, los límites de integración en Ecuación\(\ref{5.4.20}\) son\(h\) y\(l − h\), y la distancia\(y\) es\(\frac{1}{2}l − h\). En términos\(y\) del campo gravitacional en\(\text{P}\) es entonces

\[g = 2 \pi G ρ \left( 2y - \sqrt{(y + \frac{1}{2}l)^2 + a^2} + \sqrt{(y-\frac{1}{2}l)^2 + a^2} \right). \label{5.4.24} \tag{5.4.24}\]

En la gráfica de abajo he asumido, a modo de ejemplo, que\(l\) y\(a\) son ambos 1, y he trazado\(g\) en unidades de\(2 \pi Gρ\) (contando\(g\) como positivo cuando se dirige hacia abajo) de\(y = −1\) a\(y = + 1\). La porción dentro del cilindro\((- \frac{1}{2} ≤ y ≤ \frac{1}{2}l)\), representada por la Ecuación\(\ref{5.4.24}\), es casi, pero no del todo, lineal. El campo en el centro del cilindro es, por supuesto, cero.

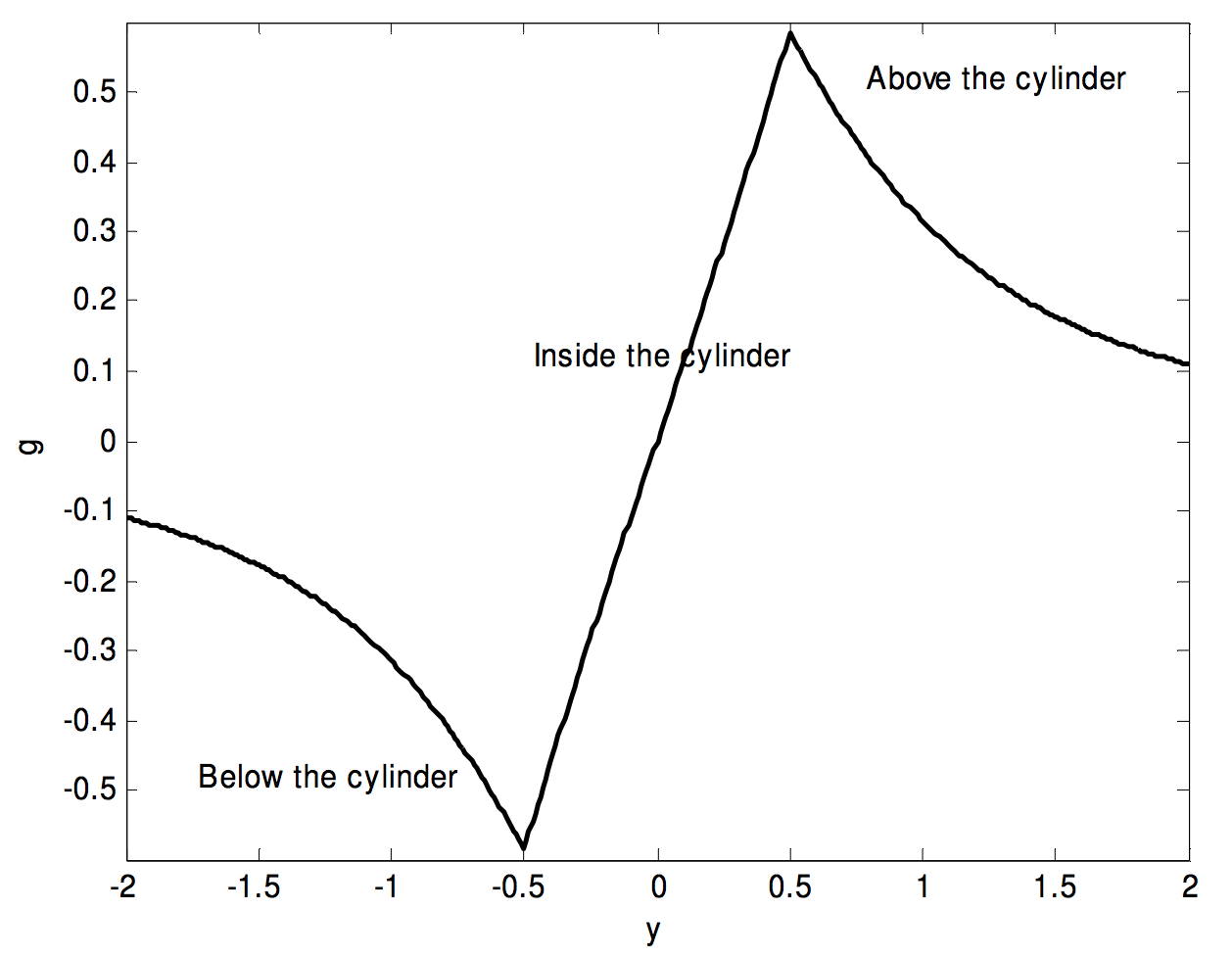
Imagen 1.png

Abajo, dibujo la misma gráfica, pero para un disco delgado, con\(a = 1\) y\(l = 0.1\). Vemos como es que el campo alcanza un máximo inmediatamente por encima o por debajo del disco, pero es cero en el centro del disco.

Imagen 2.png