17.4: Determinación de los Elementos de la Verdadera Órbita

Estoy asumiendo en esta etapa que hemos utilizado todas las observaciones más la segunda ley de Kepler y hemos determinado bien la órbita aparente, y podemos escribirla en la forma

\[ax^2 + 2hxy + by^2 + 2gx + 2fy + c = 0. \label{17.4.1} \tag{17.4.1}\]

[Los coeficientes\(a\) y\(b\) aquí, y\(e\) en la Ecuación 17.4.3, no significan, por supuesto, el semieje mayor\(a\), el semieje menor\(b\) y la eexcentricidad\(e\) de la elipse verdadera. Se piensa que el lector será poco probable que se confunda por esto, pero sin embargo he usado fuentes ligeramente diferentes para ellos.]

El origen de las coordenadas aquí es la estrella primaria, la cual, aunque está en el foco de la elipse verdadera, no está en el foco de la elipse aparente. El\(x\) eje -apunta al oeste (a la derecha) y el\(y\) eje -apunta al norte (hacia arriba), y el ángulo de posición\(θ\) (medido en sentido antihorario desde el norte) viene dado por\(\tan θ = −x/y\). Nuestra tarea es ahora encontrar los elementos de la verdadera órbita.

Durante el análisis vamos a estar obligados, en más de una ocasión, a determinar las coordenadas de los puntos donde una línea recta\(y = mx + d\) cruza la elipse, por lo que valdrá la pena prepararse para eso ahora y escribir un programa rápido para hacerlo al instante. Las coordenadas x de estos puntos están dadas por solución de\(\text{a} + 2hm + \text{b}m^2) x^2 + (2hd + 2 \text{b}md + 2g + 2fm) x + \text{b} d^2 + 2fd + c = 0, \ 17.4.2\) y las coordenadas y están dadas por solución de la Ecuación\((\text{b} + 2hn + \text{a}n^2)y^2 + (2h \text{e} + 2\text{a}n \text{e} + 2f + 2gn) y + \text{ae}^2 + 2g\text{e} + c = 0, \ 17.4.3\) donde\(n = /1 m\) y\(\text{e} = − d / m\). Si\(m\) es positivo la solución más grande para\(y\) corresponde a la solución más grande para\(x\); Si\(m\) es negativo la solución más grande para\(y\) corresponde a la solución más pequeña para\(x\).

Si la línea pasa a través\(\text{F}\), de modo que\(d = 0\), estas Ecuaciones se reducen a

\[(\text{a} + 2hm + bm^2 ) x^2 + (2g + 2fm)x + c = 0, \label{17.4.4} \tag{17.4.4}\]

y\[(\text{b} + 2hn + \text{a} n^2 ) y^2 + (2f + 2gn ) y + c = 0. \label{17.4.5} \tag{17.4.5}\]

En la figura\(\text{XVII.3}\) dibujo la verdadera elipse en el plano de la órbita. \(\text{F}\)es la estrella principal en un foco de la verdadera elipse. \(\text{C}\)es el centro de la elipse. He dibujado también el círculo auxiliar, el eje mayor (con periástrón\(\text{P}\) en un extremo y apastrón\(\text{A}\) en el otro extremo), el recto latus\(\text{MN}\) pasante\(\text{F}\) y el eje semi menor\(\text{CK}\). La relación\(\text{FC/PC}\) es la excentricidad\(\text{e}\) de la elipse verdadera, y la relación entre el eje menor y el eje mayor es\(\sqrt{1 - e^2}\). Esta es también la relación de cualquier ordenada en el círculo auxiliar a la ordenada correspondiente en la elipse. Así he extendido el recto latus y el eje semi menor por el recíproco de este factor para cumplir con el círculo auxiliar en\(\text{M}^\prime\),\(\text{N}^\prime\) y\(\text{K}^\prime\).

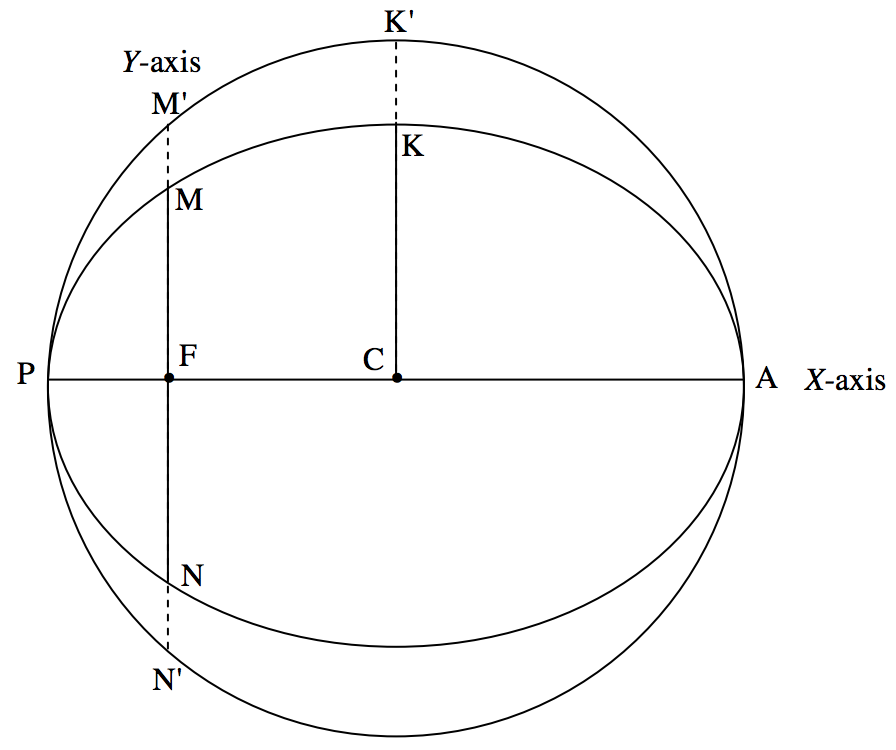
\(\text{FIGURE 17.3}\)

Ahora, en la figura\(\text{XVII.4}\), vamos a mirar lo mismo que se ve proyectado en el plano del cielo.

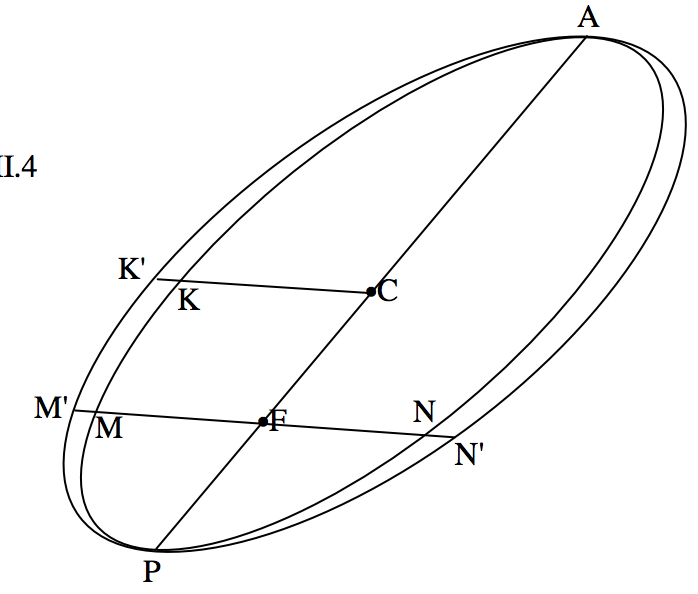
\(\text{FIGURE XVII.4}\)

La elipse verdadera se ha convertido en la elipse aparente, y el círculo auxiliar se ha convertido en la elipse auxiliar. Al inicio del análisis, solo conocemos la elipse aparente, que viene dada por la Ecuación 17.4.1, y la posición del foco\(\text{F}\), que está en el origen de las coordenadas, (0, 0). \(\text{F}\)no está en el foco de la elipse aparente, sino\(\text{C}\) que está en el centro de la elipse aparente.

Desde la sección 2.7, podemos encontrar las coordenadas (\(\bar{x} , \bar{y})\)del centro\(\text{C}\). Estas son\((\bar{g} / \bar{c} , \ \bar{f} / \bar{c})\), donde la barra denota el cofactor en el determinante de coeficientes. Así es la pendiente de la línea\(\text{FC}\), que es una porción del verdadero eje mayor\(\bar{f} / \bar{g}\). Ahora podemos escribir la Ecuación del verdadero eje mayor en la forma de\(y = mx\) ahí, mediante el uso de las Ecuaciones 17.4.4 y 5, podemos determinar las coordenadas del periástrón P y apastrón A. Ahora podemos encontrar las distancias\(\text{FC}\) y\(\text{PC}\); y la relación\(\text{FC/PC}\), que no ha cambiado en proyección, es la excentricidad\(e\) de la verdadera elipse.

Así se ha determinado e.

Nuestro siguiente paso va a ser encontrar la pendiente del recto latus proyectado\(\text{MN}\) y el semieje menor proyectado\(\text{CK}\), que es, por supuesto, paralelo al recto latus. Si la Ecuación al recto latus proyectado es\(y = mx\), podemos encontrar las\(x\) coordenadas de\(\text{M}\) y\(\text{N}\) mediante el uso de la Ecuación 17.4.4. Pero si\(\text{MN}\) es un recto latus, por supuesto está biseccionado por el eje mayor y por lo tanto la longitud\(\text{FM}\) y\(\text{FN}\) son iguales. Es decir que las dos soluciones de la Ecuación 17.4.4 son iguales en magnitud y opuestas en signo, lo que a su vez implica que el coeficiente de\(x\) es cero. Así es la pendiente del recto latus (y del eje menor)\(−g/f\).

(Se remarca de pasada que los ejes mayor y menor proyectados son diámetros conjugados de la elipse aparente, con pendientes\(\bar{f} / \bar{g}\) y\(− g / f\) respectivamente.)

Ahora que hemos determinado la pendiente del recto latus proyectado, podemos calcular fácilmente las coordenadas de\(\text{M}\) y\(\text{N}\) por solución de las Ecuaciones 17.4.4 y 17.4.5. Además,\(\text{CK}\) tiene la misma pendiente y pasa a través\(\text{C}\), cuyas coordenadas conocemos, por lo que es fácil escribir la Ecuación al eje menor proyectado en la forma\(y = mx + d\) (\(d\)es\(\bar{y} − m\bar{x}\)), y luego resolver las Ecuaciones 17.4.2 y 17.4.3 para encontrar las coordenadas de\(\text{K}\).

Ahora queremos extender\(\text{FM, FN, CK}\) a\(\text{M}^\prime , \ \text{N}^\prime \text{ and } \text{K}^\prime\). Para\(\text{M}^\prime \text{ and } \text{N}^\prime\) esto se hace y simplemente reemplazando\(x\) y\(y\) por\(kx\) y\(ky\), donde\(k\) esta el factor\(1/\sqrt{1 - e^2}\). Para\(\text{K}^\prime\), se hace sustituyendo\(x\) y\(y\) por\(\bar{x} + k(x − \bar{x})\) y\(\bar{y} + k( y − \bar{y})\) respectivamente.

Ahora tenemos cinco puntos,\(\text{P}, \ \text{A}, \ \text{M}^\prime, \ \text{N}^\prime\) y\(\text{K}^\prime\), cuyas coordenadas se conocen y que están en la elipse auxiliar. Esto es suficiente para que determinemos la Ecuación a la elipse auxiliar en forma de Ecuación\ ref {17.4.1}. Un método rápido para hacer esto se describe en la sección 2.8 del Capítulo 2.

Las pendientes de los ejes mayor y menor de la elipse auxiliar (escritas en la forma de la Ecuación 17.4.1) están dadas por

\[\tan 2θ = \frac{2h}{a - b}. \label{17.4.6} \tag{17.4.6}\]

Esta Ecuación tiene dos soluciones para\(θ\), que difieren por\(90^\circ\), las tangentes de estas son las pendientes de los ejes mayor y menor de la elipse auxiliar. Ahora que conocemos estas pendientes, podemos escribir la Ecuación a estos ejes en la forma\(y = mx + d\) (\(d\)is\(\bar{y} − m \bar{x}\)) y así podemos determinar donde los ejes cortan la elipse auxiliar y de ahí podemos determinar las longitudes de ambos ejes de la elipse auxiliar.

Esto ha sido un trabajo duro hasta el momento, pero estamos a punto de avanzar de verdad. El eje mayor de la elipse auxiliar es el único diámetro del círculo auxiliar que no ha sido acortado por proyección, y por lo tanto es igual al diámetro del círculo auxiliar, y de ahí que el eje mayor de la elipse auxiliar sea también igual al eje mayor de la elipse verdadera.

Así se ha determinado a.

La relación de las longitudes de los ejes menor a mayor de la elipse auxiliar es igual a la cantidad en la que el círculo auxiliar ha sido aplanado por proyección. Es decir, la relación de las longitudes de los ejes es igual a\(| \cos i |\). Dado que las longitudes de los ejes son esencialmente positivas, obtenemos solo\(| \cos i|\), no\(\cos i\) en sí mismo. Sin embargo, según nuestra definición de\(i\), se encuentra entre\(0^\circ\)\(180^\circ\) y y es menor o mayor que\(90^\circ\) según si el ángulo de posición del componente secundario aumenta o disminuye con el tiempo. Por ejemplo, si\(| \cos i | = \frac{1}{2} ,\)\(i\) es\(60^\circ\) o\(120^\circ\), para distinguirse por el sentido de movimiento del componente secundario.

La línea de nodos pasa\(\text{F}\) y es paralela al eje mayor de la elipse auxiliar. De hecho, esta es la razón por la que el eje mayor de la elipse auxiliar no se modificó desde su diámetro original del círculo auxiliar. Por lo tanto, ya conocemos la pendiente de la línea de nodos y de ahí conocemos el ángulo de posición del primer nodo.

Así se ha determinado Ω.

En la figura\(\text{XVII.5}\) he añadido la línea de nodos, paralela al eje mayor (no dibujado) de la elipse auxiliar. He usado los símbolos\(N\) y\(N^\prime\) para los nodos primero y segundo, pero no sabemos (y no podemos saber sin más información) cuál de estos es ascendente y cuál es descendente.

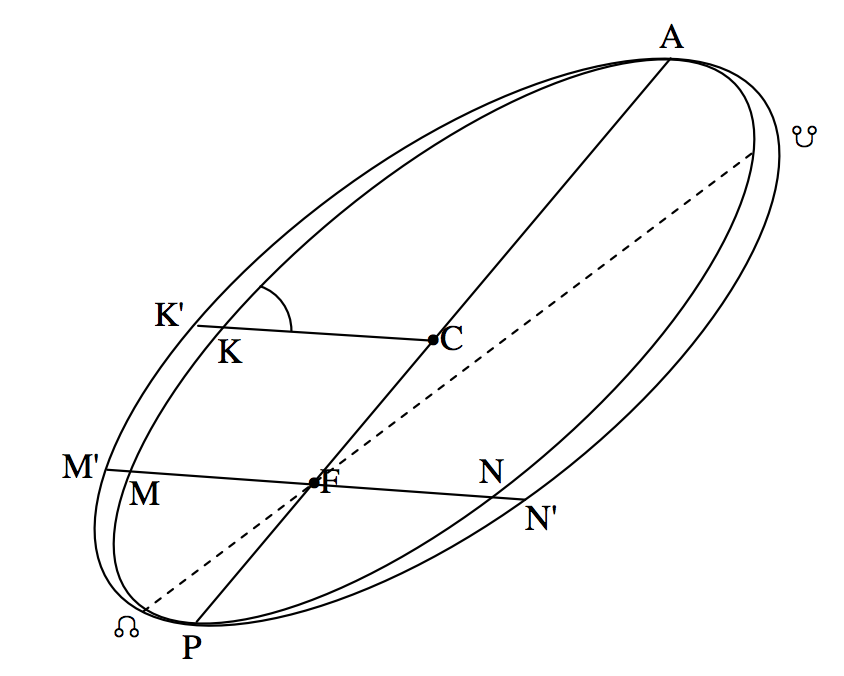
\(\text{FIGURE XVII.5}\)