18.2: La curva de velocidad a partir de los elementos

En esta sección, calculamos la curva de velocidad (es decir, cómo varía la velocidad radial con el tiempo) que se espera de una estrella con elementos orbitales dados. Por supuesto, la situación práctica es todo lo contrario: observamos la curva de velocidad, y a partir de ella, deseamos determinar los elementos. Nos ocuparemos de eso más adelante.

Voy a usar la conveniente frase “plano del cielo” para significar un plano tangente a la esfera celeste, o normal a la línea de visión del observador al centro de masa del sistema. El centro de masa C del sistema, entonces, está estacionario en el plano del cielo. El plano de las órbitas de las dos estrellas alrededor de su centro de masa está inclinado en un ángulo i con respecto al plano del cielo. Voy a seguir las aventuras de la estrella 1 sobre el centro de masa C. ¡Y voy a asumir que el Capítulo 9 está todo fresco en tu mente!

El eje semi mayor de la órbita de la estrella 1 alrededor de C es un ₁, y el recto semi latus\(l_{1}=a_{1}\left(1-e^{2}\right)\). El momento angular por unidad de masa de estrella 1 sobre C es\(r_{1}^{2} \dot{v}=\sqrt{G M l_{1}}\), donde v es la verdadera anomalía y\( \mathrm{M}=m_{2}^{3} /\left(m_{1}+m_{2}\right)^{2}\). El periodo orbital P viene dado por\(P^{2}=\frac{4 \pi^{2}}{G M} a_{1}^{3}\). El movimiento medio n es 2p/ P, y por lo tanto n ² a ₁ ³ = GM. Por lo tanto, el momento angular por unidad de masa es

\[r_{1}^{2} \dot{v}=n a_{1}^{2} \sqrt{1-e^{2}}.\]

En la figura XVIII.1 vemos la estrella 1 (etiquetada S) en órbita alrededor de C, y en algún momento el argumento de latitud de S es θ, y su distancia desde C es r ₁. Su distancia por encima del plano del cielo es z, y r ₁ sin β. La inclinación del plano de la órbita al plano del cielo es i, y, para encontrar una expresión para β en términos del argumento de latitud y la inclinación, sólo voy a dibujar, en la figura VIII.2, estos ángulos sobre la superficie de una esfera. La esfera está centrada en C, y es de radio arbitrario.

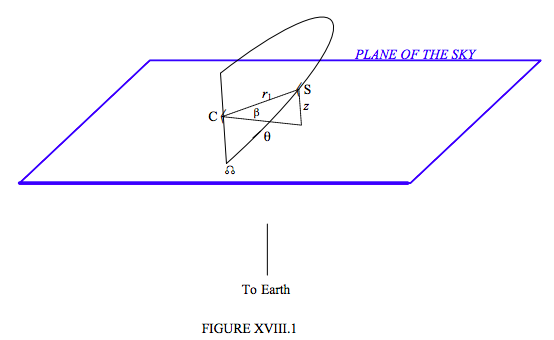
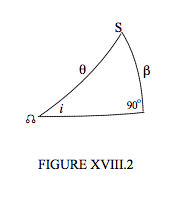
Vemos de este triángulo que sin β = sin i sin θ. Además, el argumento de latitud θ = ω + v, (ω = argumento de periastrón, v = anomalía verdadera), y así

\[z=r_{1} \sin i \sin (\omega+v).\]

En este momento, la velocidad radial V de la estrella 1 relativa al Sol viene dada por

\[V=V_{0}+\dot{z},\]

donde V ₀ es la velocidad radial del centro de masa C, o la velocidad sistémica. Diferenciación de la Ecuación 18.2.1 con respecto al tiempo da

\[\dot{z}=\sin \left[\dot{r}_{1} \sin (\omega+v)+r_{1} \dot{v} \cos (\omega+v)\right].\]

Me gustaría expresar esto enteramente en términos de la verdadera anomalía v en lugar de v y r ₁. La ecuación a la elipse es

\[ r_{1}=\frac{l_{1}}{1+e \cos v}=\frac{a_{1}\left(1-e^{2}\right)}{1+e \cos v},\]

donde l ₁ es el recto semi latus, y así

\[\dot{r}_{1}=\frac{l_{1} e \dot{v} \sin v}{(1+e \cos v)^{2}}=\frac{r_{1} e \dot{v} \sin v}{1+e \cos v}.\]

lo que ayuda un poco. Así tenemos

\[\frac{\dot{z}}{\sin i}=r_{1} \dot{v}\left(\frac{e \sin v \sin (\omega+v)}{1+e \cos v}+\cos (\omega+v)\right).\]

También podemos hacer uso de la Ecuación 18.2.1 y, con alguna ayuda de la Ecuación 18.2.5, obtenemos

\[\frac{\dot{z}}{\sin i}=\frac{n a_{1}(1+e \cos v)}{\sqrt{1-e^{2}}}\left(\frac{e \sin v \sin (\omega+v)}{1+e \cos v}+\cos (\omega+v)\right)\]

o

\[\frac{\dot{z}}{\sin i}=\frac{n a_{1}}{\sqrt{1-e^{2}}}(e \sin v \sin (\omega+v)+(1+e \cos v) \cos (\omega+v)).\]

Ahora e sin v sin (ω + v) + e cos v cos (ω + v) = e cosω, entonces nos quedamos con

\[\dot{z}=\frac{n a_{1} \sin i}{\sqrt{1-e^{2}}}(\cos (\omega+v)+e \cos \omega).\]

A la cantidad\(\frac{n a_{1} \sin i}{\sqrt{1-e^{2}}}\), que tiene las dimensiones de velocidad, generalmente se le da el símbolo K ₁, de manera que

\[\dot{z}=K_{1}(\cos (\omega+v)+e \cos \omega),\]

y así la velocidad radial (incluyendo la velocidad sistémica) en función de la verdadera anomalía y los elementos viene dada por

\[V=V_{0}+K_{1}(\cos (\omega+v)+e \cos \omega).\]

Se puede ver que\(\dot{z}\) varía entre K ₁ (1 e cos ω) y - K ₁ (1 - e cos ω), y que K ₁ es la semiamplitud de la curva de velocidad radial.

La ecuación 18.2.12 da la velocidad radial en función de la verdadera anomalía. Pero realmente queremos la velocidad radial en función del tiempo. Esto es fácil, o al menos directo, porque ya sabemos calcular la verdadera anomalía en función del tiempo. Doy aquí las Ecuaciones pertinentes. He conservado su numeración original, para que pueda localizarlos en los capítulos anteriores.

\[ M=\frac{2 \pi}{P}(t-T) \]

\[ M=E-e \sin E\]

\[\cos v=\frac{\cos E-e}{1-e \cos E}\]

A partir de identidades trigonométricas, esto también se puede escribir

\[\sin v=\frac{\sqrt{1-e^{2}} \sin E}{1-e \cos E} \]

o

\[ \tan v=\frac{\sqrt{1-e^{2}} \sin E}{\cos E-e} \]

o

\[ \tan \frac{1}{2} v=\sqrt{\frac{1+e}{1-e}} \tan \frac{1}{2} E\]

En las figuras XIII.3 y XIII.4 muestro dos ejemplos de curvas de velocidad. La figura XIII.3 se calcula para e = 0.5, ω = 0 ^o. La figura XIII.4 se calcula para e = 0.75, ω = 90 ^o.

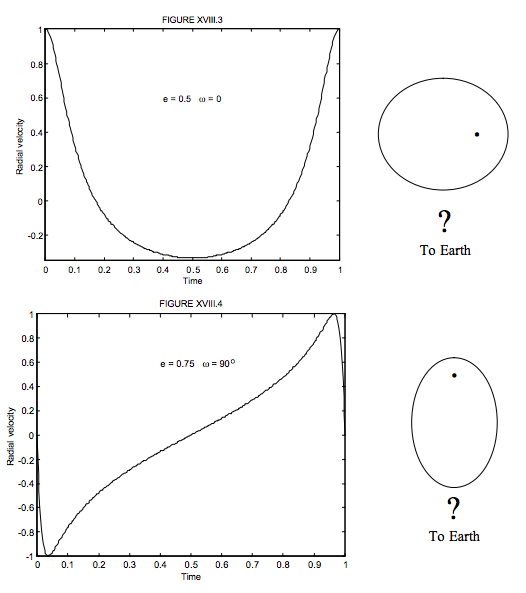
Para dibujar estas dos figuras, se adivinará correctamente que he escrito un programa informático que calculará las Ecuaciones 9.6.4, 9.6.5, 2.3.16 y 18.2.12 en orden, para los valores elegidos de e y ω. Esto es perfectamente sencillo excepto que la Ecuación 9.6.5, la Ecuación de Kepler, requiere cierta iteración. La solución de la Ecuación de Kepler se discutió en la Sección 9.6. Si en serio me iba a interesar computar las órbitas de las estrellas binarias espectroscópicas en esta etapa utilizaría este programa para generar e imprimir 360 curvas de velocidad radial para 36 valores de ω que van de 0 ^o a 350 ^o y diez valores de e pasando de 0.0 a 0.9. Entonces, cuando tenía una curva de velocidad radial real de una estrella binaria espectroscópica real para analizar, podría compararla con mi conjunto de curvas teóricas y de ahí poder obtener al menos una primera aproximación aproximada a la excentricidad y argumento del periastrón.

He dibujado las figuras XVIII.3 y 4 para una velocidad sistémica V ₀ de cero. Una verdadera estrella no tendrá una velocidad sistémica cero y de hecho uno de los objetivos debe ser determinar la velocidad sistémica.

Así en la figura XVIII.5 he dibujado una curva de velocidad radial (no estoy diciendo cuáles son los valores de ω y e), pero esta vez no he asumido una velocidad radial sistémica cero. Se notará que la estrella observada pasa mucho más tiempo moviéndose hacia nosotros que alejándose de nosotros. Si dibujamos una línea horizontal Velocidad Radial = V ₀ a través de la figura, esta línea debe ser dibujada de tal manera que el área entre ella y la curva de velocidad radial por encima de ella sea igual al área entre ella y la curva de velocidad radial por debajo de ella. ¿Cómo posicionar esta línea? Esa es una buena pregunta. Si nada más, puedes contar cuadrados en papel cuadriculado. Eso al menos te dará una primera idea aproximada de cuál es la velocidad sistémica.

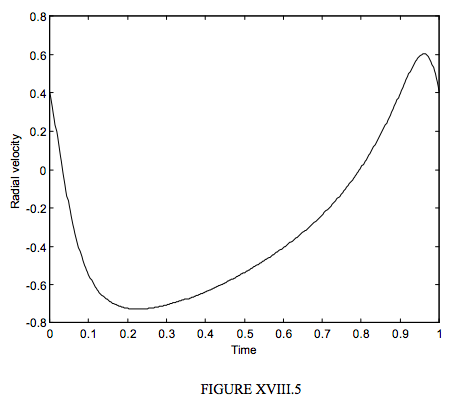
Si tienes un binario de doble línea, tendrás dos curvas de velocidad radial. No son exactamente imágenes especulares entre sí; la semiamplitud de cada componente es inversamente proporcional a su masa. Pero la velocidad sistémica es entonces fácil, porque las dos curvas se cruzan cuando la velocidad radial de cada una es igual a la velocidad radial del sistema.