2.2F: Potencial en el Plano de un Anillo Cargado

Suponemos que tenemos un anillo de radio a portando una carga\(Q\). Intentaremos encontrar el potencial en un punto del plano del anillo y a una\(r\)\((0 ≤ r < a)\) distancia del centro del anillo.

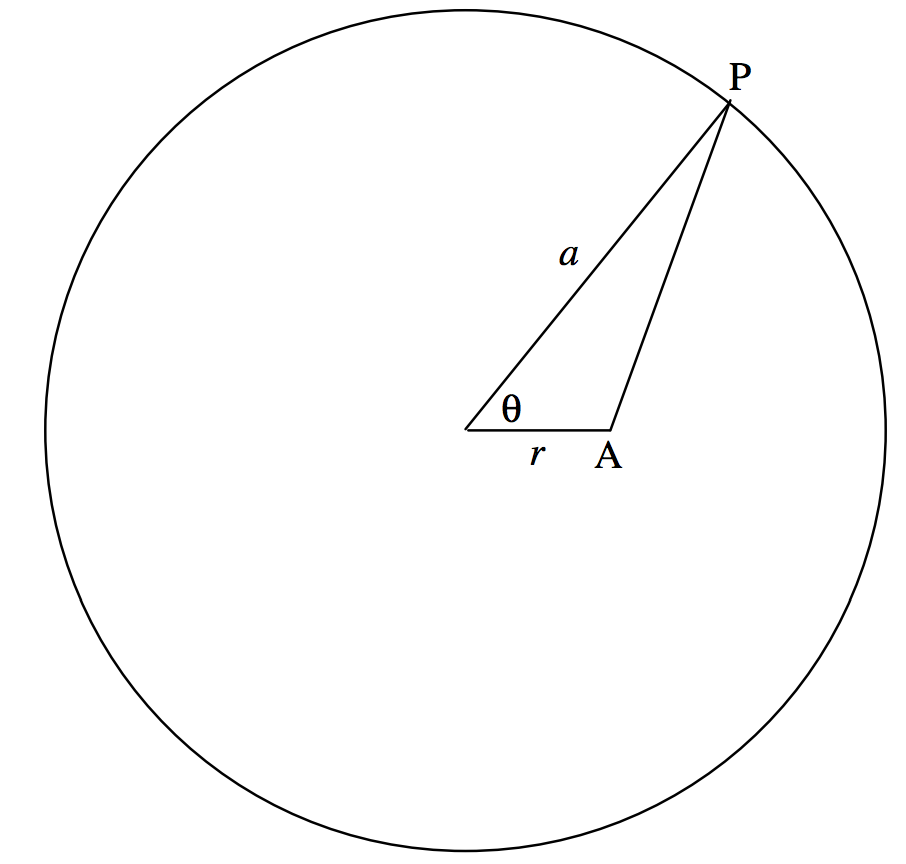
Considera un elemento\(δθ\) del anillo en P. La carga en él es\(\frac{Q\delta \theta}{2\pi}\). El potencial en A debido a este elemento de carga es

\[\frac{1}{4\pi\epsilon_0}\cdot \frac{Q\delta \theta}{2\pi}\cdot \frac{1}{\sqrt{a^2+r^2-2ar\cos \theta}}=\frac{Q}{4\pi\epsilon_0 2\pi a}\cdot \frac{\delta \theta}{\sqrt{b-\cos \theta}},\tag{2.2.9}\]

dónde\(b=1+r^2/a^2\) y\(c = 2r / a\). El potencial debido a la carga en todo el anillo es

\[V=\frac{Q}{4\pi\epsilon_0 \pi a}\int_0^\pi \frac{d\theta}{\sqrt{b-c\cos \theta}}.\tag{2.2.10}\]

No puedo ver de inmediato una solución analítica a esta integral, por lo que la integré numéricamente de\(r = 0\) a\(r = 0.99\) en pasos de\(0.01\), con el resultado mostrado en la siguiente gráfica, en la que\(r\) está en unidades de\(a\), y\(V\) está en unidades de\(\frac{Q}{4\pi\epsilon_0 a}\).

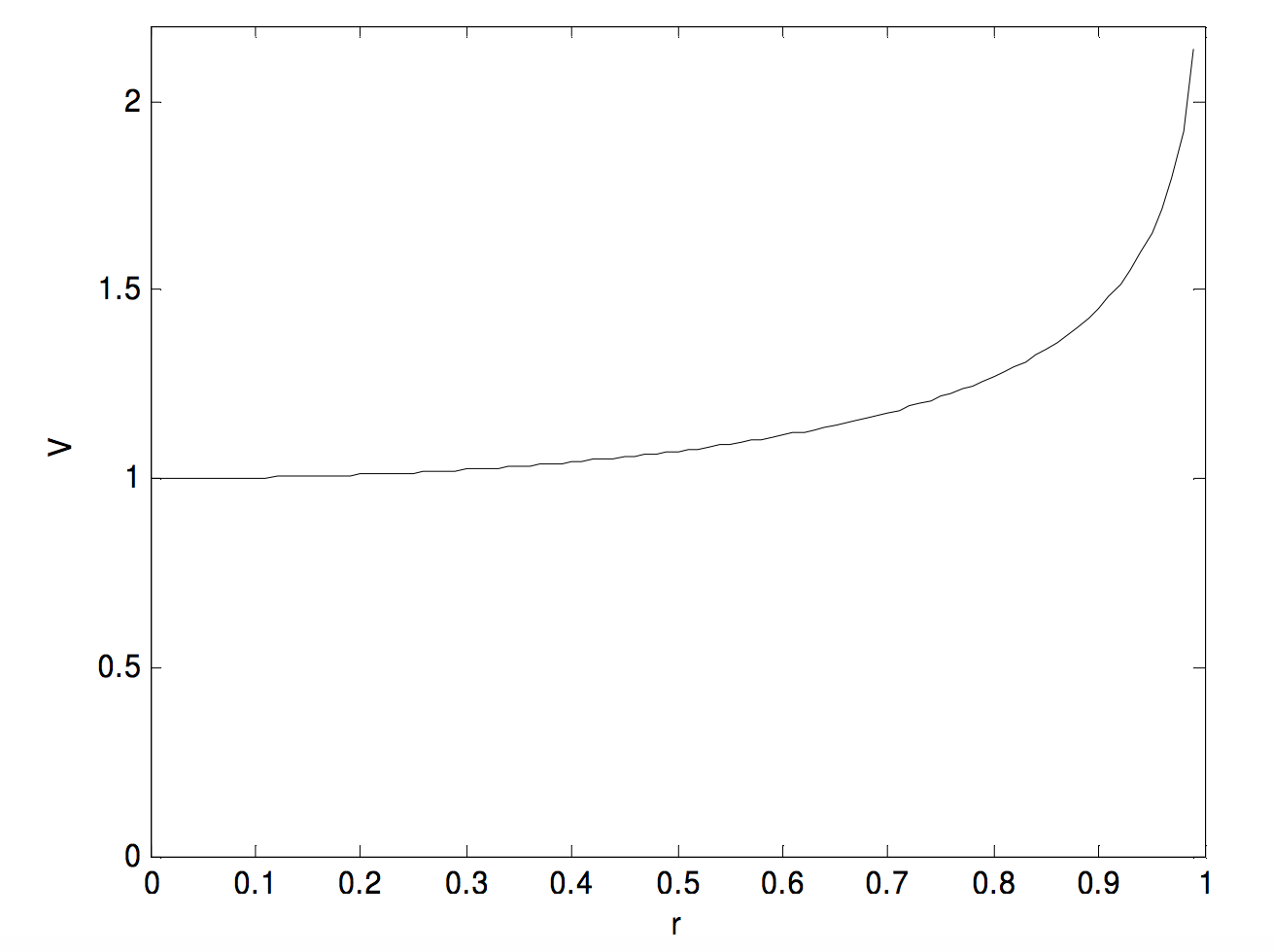
El campo es igual al gradiente de éste y se dirige hacia el centro del anillo. Parece que una pequeña carga positiva estaría en equilibrio estable en el centro del anillo, y esto sería así si la carga se viera obligada a permanecer en el plano del anillo. Pero, sin tal restricción, la carga se alejaría del anillo si se desvía en absoluto por encima o por debajo del plano del anillo.

Algunas notas computacionales.

Cualquier lector que haya intentado reproducir estos resultados habrá descubierto que más bien se requiere mucho cálculo pesado. Al no existir una expresión analítica simple para la integración, cada uno de los 100 puntos a partir de los cuales se computó la gráfica implicó una integración numérica de la expresión para el potencial. Encontré que la Regla de Simpson no dio resultados muy satisfactorios, principalmente por el fuerte aumento de la función en general\(r\), por lo que usé cuadratura gaussiana, que resultó mucho más satisfactoria.

¿Podemos evitar la integración numérica? Una posibilidad es expresar el integrando en la ecuación 2.2.10 como una serie de potencias en\(\cos θ\), y luego integrar término por término.

Así\(\sqrt{b-c\cos \theta}=\sqrt{b}\sqrt{1-e\cos \theta}\), dónde\(e=\frac{c}{b}=\frac{2(r/a)}{(r/a)^2+1}\). Y luego

\(\sqrt{1-r\cos \theta}=1+\frac{1}{2}e\cos \theta + \frac{3}{8}e^2 \cos^2 \theta +\frac{5}{16}e^3\cos^3 \theta +\frac{35}{128}e^4\cos^4 \theta + \frac{231}{1024}e^5 \cos^5 \theta +\frac{63}{256}e^6 \cos^6 \theta+\frac{231}{1024}e^7 \cos^7 \theta + \frac{715}{32768}e^8\cos^8 \theta + ... \tag{2.2.11}\)

Entonces podemos integrar este término por término, usando\(\int_0^\pi \cos^n \theta \, d\theta = \frac{(n-1)!!\pi}{n!!}\) si\(n\) es par, y obviamente cero si\(n\) es impar.

Finalmente conseguimos:

\[V=\frac{Q}{4\pi\epsilon_0 a}(1+\frac{3}{16}e^2+\frac{105}{1024}e^4+\frac{1155}{16384}e^6+\frac{25025}{4194304}e^8 ...).\tag{2.2.12}\]

Para fines computacionales, esto se renderizará de manera más eficiente como

\[V=\frac{Q}{4\pi\epsilon_0 a}(1+e^2(\frac{3}{16}+e^4(\frac{105}{1024}+e^6(\frac{1155}{16384}+\frac{25025}{4194304}e^8)))).\tag{2.2.14}\]

Me referiré a esto como Serie I. Resulta que no es una serie muy eficiente, ya que converge muy lentamente. Esto se debe a que e no es una fracción pequeña, y siempre es mayor que\(r/a\). Así para\(r/a=\frac{1}{2},\, e=0.8\).

Podemos hacerlo mucho mejor si podemos obtener una serie de potencia en\(r/a\). Consideremos la expresión\(\frac{1}{\sqrt{a^2+r^2-2ar\cos \theta}}=\frac{1}{a\sqrt{1+(r/a)^2-2(r/a)\cos \theta}}\), que ocurre en la ecuación 2.2.9. Esta expresión, y otras muy similares a ella, ocurren con bastante frecuencia en diversas situaciones físicas. Se puede ampliar por el teorema binomial para dar una serie de poder en\(r/a\). (Es cierto que es una expresión trinomial, pero hágala por etapas). El resultado es

\[(1+(r/a)^2-2(r/a)\cos \theta )^{-1/2}=P_0 (\cos \theta)+P_1(\cos \theta )(\frac{r}{a} ) + P_2 (\cos \theta)(\frac{r}{a})^2+P_3 (\cos \theta )(\frac{r}{a})^3 + ... \tag{2.2.15}\]

donde los coeficientes de las potencias de\((\frac{r}{a})\) son polinomios en\(\cos θ\), que han sido tabulados extensamente en muchos lugares, y se denominan polinomios de Legendre. Véase, por ejemplo, mis notas sobre Mecánica Celestial, http://orca.phys.uvic.ca/~tatum/celmechs.html Secciones 1.1.4 y 5.11. Cada término en los polinomios de Legendre puede entonces integrarse término por término, y la serie resultante, después de un poco de trabajo, es

\[V=\frac{Q}{4\pi\epsilon_0 a}(1+\frac{1}{4}(\frac{r}{a})^2+\frac{9}{64}(\frac{r}{a})^4+\frac{25}{256}(\frac{r}{a})^6+\frac{1225}{16384}(\frac{r}{a})^8...).\tag{2.2.16}\]

Dado que se trata de una serie en\((\frac{r}{a})\) lugar de en\(e\), converge mucho más rápido que la ecuación 2.2.13. Me referiré a ella como serie\(II\). Por supuesto, para fines computacionales debe escribirse con paréntesis anidados, como hicimos para la serie I en la ecuación 2.2.14.

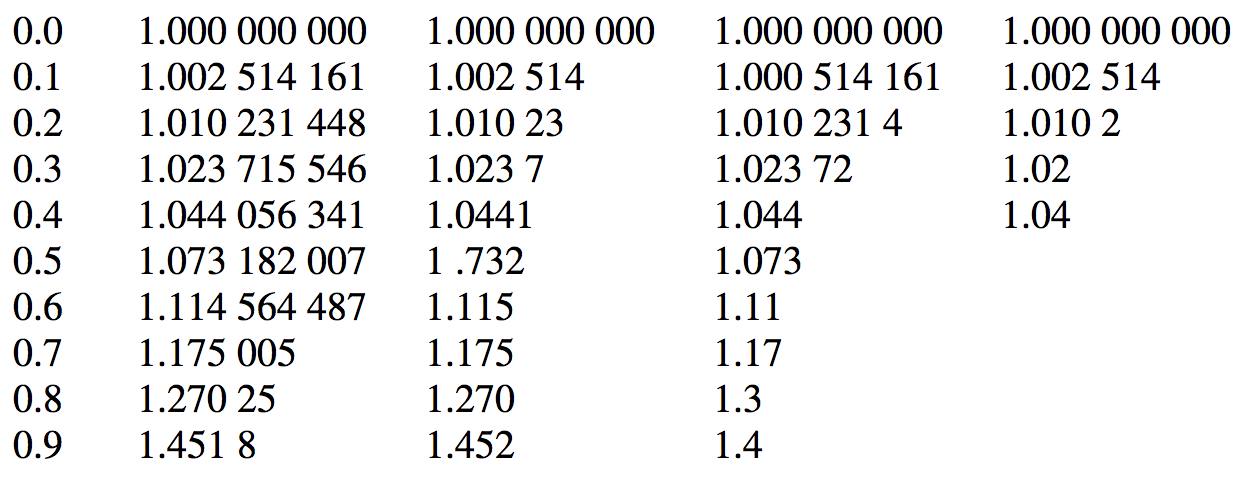
Aquí hay una tabla de los resultados utilizando cuatro métodos. La primera columna da el valor de\(r/a\). Las siguientes cuatro columnas dan los valores de\(V\), en unidades de a\(\frac{Q}{4\pi\epsilon_0 a}\), calculados por cuatro métodos. Columna 2, integración por cuadratura gaussiana. Columna 3, integración por la Regla de Simpson. Columna 4, aproximación por Serie I. Columna 5, aproximación por serie\(II\). En cada caso he dado el número de dígitos que creo que son confiables. Se ve que la cuadratura gaussiana da con mucho los mejores resultados. \(I\)La serie no es muy buena en absoluto, mientras que la Serie\(II\) es casi tan buena como la Regla de Simpson.

Por supuesto cualquiera de estos métodos se completa casi instantáneamente en una computadora moderna, por lo que uno puede preguntarse si vale la pena dedicar mucho tiempo buscando la solución más eficiente. Eso dependerá de si uno quiere hacer el cálculo solo una vez, o si quiere hacer cálculos similares millones de veces.